数形结合思想在初中数学教学中的渗透探究

费德清

【摘 要】“数形结合”思想是初中数学阶段一种重要的解题方法，也是初中教学中非常重要的内容，可以拓展学生的数学思维，培养学生创新能力、探索能力。为了顺应新课程改革的需求，初中数学教学应该将“数形结合”与探究性学习结合起来，培养学生“数形结合”的思维方式，为学生数学学习打下稳固的基础。

【关键词】数形结合;初中;数学教学;渗透

一、渗透数形结合的思想，养成用数形结合分析问题的意识

在我们的日常生活中各种不同的图形知识当中，处处可见数形结合的思想，比如温度计与其上面的温度，运动场上的100米跑道，初中教材中的数与数轴;一元一次不等式的解集与一次函数的图像等等，在实际教学中，教师应该善于借助生活中的一些例子，充分贴近于生活，深入钻研教材，对学生进行逐步的引导，比如在学习数轴的知识时，我们便可以借助温度计或者刻度尺来辅助学习，使之与数轴上的各个点建立一一对应的关系，有助于学生对相反数和绝对值的理解和掌握，通过数轴来进行有理数大小的比较，从而培养他们通过数形结合思想来解决问题的意识。

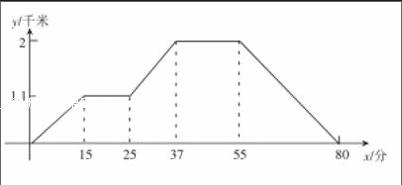
例：下面所示的图像是李华从家离出发到超市买东西，又去奶奶家玩，然后回家。李华家、超市、奶奶家在一条直线上。根据图像回答问题：

①超市和李华家距离多远？他从家到超市以供花费了多长时间？

②李华在超市买东西多长时间？

③超市和奶奶家离了多远？李华从超市到奶奶家用了多长时间？

④李华在奶奶家待了多长时间？

⑤奶奶家和李华家距离有多远？李华从奶奶家到家的平均速度是多少？

通过这种紧密贴合现实生活的问题，通过反复渗透，从而使学生在数学学习的过程中逐渐形成数形结合的意识。

二、通过例题分析，展示数学思想方法

例题是数学教学中讲授新知识的重要方式，同时也是学生获取数学知识、学习数学思想方法的重要渠道。通过例题的讲解和分析，能够将其中包含的数学思想进行融入和渗透，让学生在教学中对数学思想和方法有了更加深刻的感悟和理解。在数学教材中，很多非常典型的例题中都蕴含了丰富的数学思想和方法，因此，数学教师应该深入研读教材，潜心挖掘其中核心的思想和方法。

例1：根据下图所示的图形变化规律，找出其中的规律填上正确的数字，并简述理由。

观察得知：图中第一组图形由一个小正方形组成，第二个图形由三个小正方形，第三组为六个，从前三组图像分析得知，第二组图形中的小正方体比第一组的小正方体多两个，第三组图形中的小正方体比第二组的小正方体多三个，那么由此规律可知，第四组图形中的小正方体就比第三组多四个，那么第四组就有十个小正方体，以此类推，第五个组图形比第四个多五个小正方体，第五组图形就有十五个小正方体，第六组就有二十一个小正方体，第n组图像就有1+2+3+4+5+6……+n=，这道题目充分了体现了数形结合的思想，通过这道题目的分析可知，教师在解答题目时，将所包含的数学思想得以体现，通过对问题的提炼，在例题中充分体现了“几何建模”以及“转化”的数学思想，通过教师的引导和帮助，学生学会了将复杂问题通过转化使之更加简化的方法和技巧。

三、通过数学实践活动，体会数学思想方法

数学学习的过程实质上是一个‘做数学的过程，学生对通过亲身参与到数学学习中对数学思想进行深入的理解和认识，观察、试验、归纳、类比等数学方法和学生的实践活动密不可分，集合、对应、函数、数形结合、概率统计、转化、数列、排列组合、公理化等数学思想，使学生通过在学习中不断的实践探索中加以感悟和理解，并达到融会贯通的目的。

例2：如图所示l1、l2分别表示B、A两船相对于海岸的距离s与追赶时间t之间的关系。根据图像回答：如果时间t为多少时，快艇B能追上A。

根据图像分析得知。首选分别确定l1，l2，接着将这两个函数式组成一个方程组，解出方程组的解便得到这个位置的坐标，最终得出答案为：当t为15分钟时，快艇B将追赶上A。

在数学实践活动中，学生对“函数、观察和转化、试验”的数学思想以及方法进行了全面的理解和掌握，从而为他们相关知识点的学习打下了良好的基础

四、结束语

总而言之，在初中数学教学中，数学教师深入钻研教材的思想和内涵，充分挖掘教材，不断开发出教材的价值，通过引导和帮助，逐渐使学生建立数相结合的思想，通过创设相应的情境，使学生在整个学习过程中掌握基本的思想方法和理念，提升其分析问题、解决问题的能力，提升数学教学水平。

参考文献：

[1]孙雅琴.渗透数学基本思想的初中数学课堂教学实践研究[D].重庆师范大学，2012.