偏序度量空间中混合单调随机算子的耦合重合点定理

李承耕，许绍元，刘 波

(韩山师范学院数学与应用数学系，广东 潮州 521041)

偏序度量空间中混合单调随机算子的耦合重合点定理

李承耕，许绍元，刘 波

(韩山师范学院数学与应用数学系，广东 潮州 521041)

研究了偏序度量空间中的随机混合单调算子，并将一般混合单调算子的重合点定理扩展到随机混合单调算子的耦合重合点定理，推广了已有文献的一些结论.

偏序；耦合重合点：混合单调算子；随机算子

1 预备知识

混合单调算子是一类非常重要的算子，它于1987年由郭大钧和Lakshmikantham[1-2]提出后，众多学者对其做了大量研究，得到一批很好的结果.[2-9]它的很多理论已被应用于非线性微分方程与非线性积分方程解的存在性问题的研究中.本文在文献[1-3]的基础上，讨论了两类混合单调算子随机耦合重合点问题，修改了文献[3]给出的压缩条件，并在新的压缩条件下讨论了随机耦合重合点的存在性与唯一性问题，得到了与文献[3]相区别的一些结论.

定义1[5]设(X，d)是一个偏序集，映射F:X×X→X和g:X→X满足：(1) 若g(x1)≤g(x2)，则F(x1，y)≤F(x2，y)；(2) 若g(y1)≤g(y2)，则F(x，y2)≤F(x，y1).则称算子F(x，y)具有混合g-单调性，即F(x，y)对x具有g-单调非减性，F(x，y) 对y具有g-单调非增性.

定义2[5]对于算子F:X×X→X和g:X→X，如果F(x，y)=g(x)，且F(y，x)=g(y)，则称元素(x，y)为F对g的一个耦合重合点.

定义3[3]对于随机算子F:Ω×(X×X)→X，若满足：(1)∀ω∈Ω，F(ω，·)连续；(2)∀v∈X×X，F(·，v)可测.则称F是连续随机算子.

2 主要结果

设(X，≤)是一个偏序集，(X，d)是完备可分度量空间，(Ω，Σ)为可测空间，F:Ω×(X×X)→X和g:Ω×X→X为混合单调算子.本文做如下假设：

(A1)F(ω，·)和g(ω，·)是连续的，∀ω∈Ω.

(A2)F(·，v)和g(·，x)是可测的，∀v∈X×X，∀x∈X.

(A3)F(ω×(X×X))⊆X，对每个ω∈Ω.

(A4)g是连续的，对F是可交换的.

(A5)F是连续的.

(A6)X满足:如果一个非减序列xn→x，则xn≤x对任意的n成立；如果一个非增序列xn→x，则x≤xn对任意的n成立.

定理1 设(X，≤)是一个偏序集，(X，d)是完备可分度量空间，(Ω，Σ)为可测空间，F:Ω×(X×X)→X和g:Ω×X→X为混合单调算子.对任意α+β<1，α>0，β>0，ω∈Ω，不等式

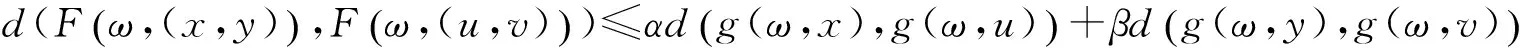
对所有满足g(ω，x)≤g(ω，u)，g(ω，y)≥g(ω，v)的x，y，u，v∈X成立，且假设(A1)—(A6)成立.如果存在可测映射ξ0，η0∈X，使得g(ω，ξ0(ω))≤F(ω×(ξ0(ω)，η0(ω)))，F(ω×(η0(ω)，ξ0(ω)))≤g(ω，η0(ω))，则也存在可测映射ξ，θ:Ω→X，使得F(ω×(ξ(ω)，θ(ω)))=g(ω，ξ(ω))，F(ω×(θ(ω)，ξ(ω)))=g(ω，θ(ω))， ∀ω∈Ω.即F和g存在耦合随机重合点.

证明 设Θ={ξ|Ω→X}是一个可测映射类.定义函数h:Ω×X→R+，h(ω，x)=d(x，g(ω，x))，则由已知条件，h(ω，·)连续，h(·，x)可测，从而h(ω，x)是Caratheodory函数.故当ξ:Ω→X可测时，ω→h(ω，ξ(ω)) 也是可测的.∀ξ∈Θ，定义η(ω)=g(ω，ξ(ω))，则η:Ω→X也是可测的，η∈Θ.

g(ω，ξ1(ω))=F(ω，(ξ0(ω)，η0(ω)))，g(ω，η1(ω))=F(ω，(η0(ω)，ξ0(ω)))，

这样确定了ξ1，η1；再由F(ω，(ξ1(ω)，η1(ω)))∈X=g(ω×X)，F(ω，(η1(ω)，ξ1(ω)))∈X=g(ω×X)，存在ξ2，η2∈Θ使得

g(ω，ξ2(ω))=F(ω，(ξ1(ω)，η1(ω)))，g(ω，η2(ω))=F(ω，(η1(ω)，ξ1(ω)))，

g(ω，ξn+1(ω))=F(ω，(ξn(ω)，ηn(ω)))，g(ω，ηn+1(ω))=F(ω，(ηn(ω)，ξn(ω))).

(1)

下面用数学归纳法证明

g(ω，ξn(ω))≤g(ω，ξn+1(ω))，g(ω，ηn(ω))≥g(ω，ηn+1(ω))，n≥0.

(2)

当n=0时，g(ω，ξ0(ω))≤F(ω，(ξ0(ω)，η0(ω)))，g(ω，η0(ω))≥F(ω，(η0(ω)，ξ0(ω)))，即g(ω，ξ0(ω))≤g(ω，ξ1(ω))，g(ω，η0(ω))≥g(ω，η1(ω))，从而当n=0时，结论成立.假设对任意的n≥0，结论成立，即

g(ω，ξn(ω))≤g(ω，ξn+1(ω))，g(ω，ηn(ω))≥g(ω，ηn+1(ω)).

下证对n+1时结论成立.事实上，由F对于第一个变量具有单调g-非减性，

F(ω，(ξn(ω)，ηn(ω)))≤F(ω，(ξn+1(ω)，ηn(ω)))，

F(ω，(ηn+1(ω)，ξn(ω)))≤F(ω，(ηn(ω)，ξn(ω))).

(3)

由F对于第二个变量具有单调g-非增性，

F(ω，(ξn+1(ω)，ηn+1(ω)))≥F(ω，(ξn+1(ω)，ηn(ω)))，

F(ω，(ηn+1(ω)，ξn(ω)))≥F(ω，(ηn+1(ω)，ξn+1(ω))).

(4)

由(3)—(4)式及不等式的传递性有

F(ω，(ξn+1(ω)，ηn+1(ω)))≥F(ω，(ξn(ω)，ηn(ω)))，

F(ω，(ηn(ω)，ξn(ω)))≥F(ω，(ηn+1(ω)，ξn+1(ω)))，

从而g(ω，ξn+1(ω))≤g(ω，ξn+2(ω))，g(ω，ηn+1(ω))≥g(ω，ηn+2(ω))，即结论在n+1时成立.

定义δn=d(g(ω，ξn(ω))，g(ω，ξn+1))+d(g(ω，ηn(ω))，g(ω，ηn+1(ω))).注意到

d(g(ω，ξn(ω))，g(ω，ξn+1))=

d(F(ω，(ξn-1(ω)，ηn-1(ω)))，F(ω，(ξn(ω)，ηn(ω))))≤

αd(g(ω，ξn-1(ω))，g(ω，ξn))+βd(g(ω，ηn-1(ω))，g(ω，ηn(ω)))，

(5)

d(g(ω，ηn(ω))，g(ω，ηn+1))=

d(F(ω，(ηn-1(ω)，ξn-1(ω)))，F(ω，(ηn(ω)，ξn(ω))))≤

αd(g(ω，ηn-1(ω))，g(ω，ηn))+βd(g(ω，ξn-1(ω))，g(ω，ξn(ω)))，

(6)

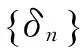
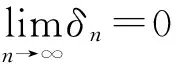
现在证明{g(ω，ξn(ω))}和{g(ω，ηn(ω))}是柯西列，用反证法.若{g(ω，ξn(ω))}和{g(ω，ηn(ω))}至少有一个不是柯西列，则存在ε>0，和两个正整数序列{m(k)}，{l(k)}，m(k)>l(k)>k，满足：

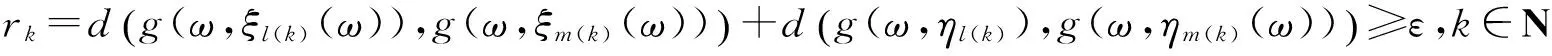
(7)

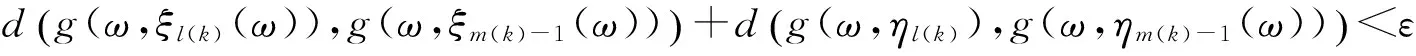
(8)

实际上可以选择使得(7)式成立的最小m(k)，此时必然可以使得(8)式成立.由(7)—(8)式与三角不等式有

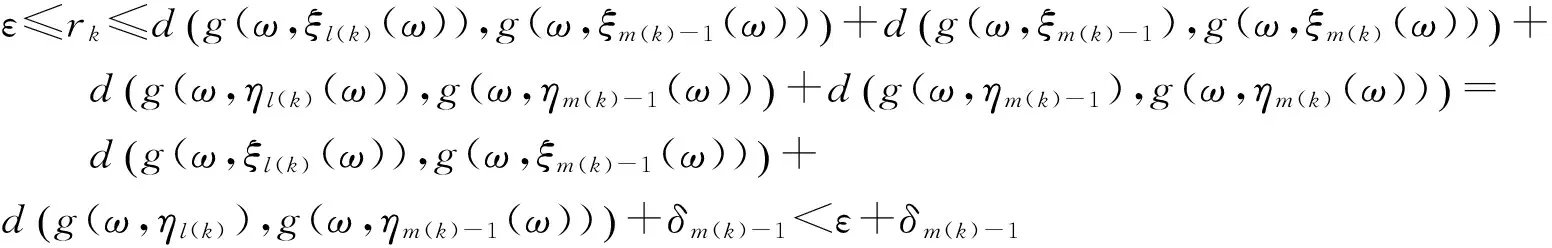
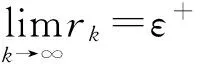
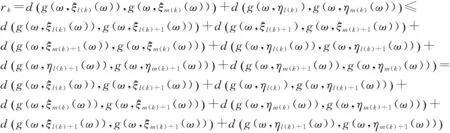
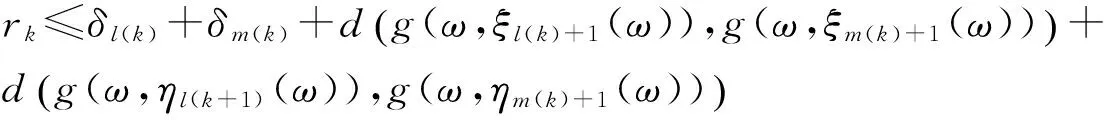
(9)

而

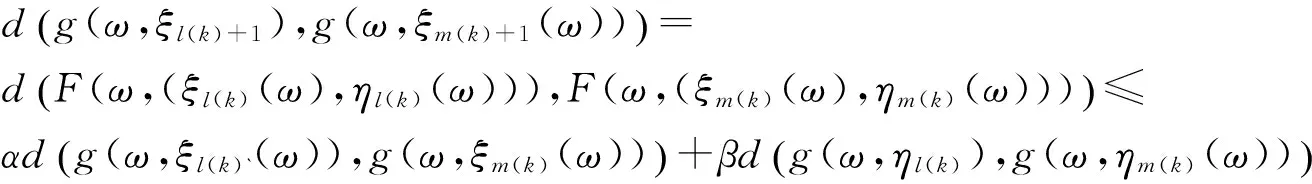
(10)

(11)

(10)和(11)式相加得

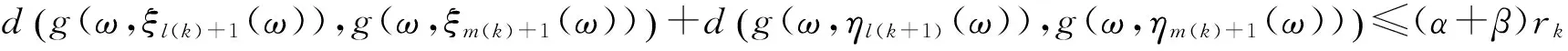
将之代入(9)式得rk≤δl(k)+δm(k)+(α+β)rk，令k→∞有ε≤0+0+(α+β)ε<ε，矛盾.故假设不成立，{g(ω，ξn(ω))}和{g(ω，ηn(ω))}是柯西列.

由g(X×X)=X的完备性，存在θ0，ξ0∈Θ，使得

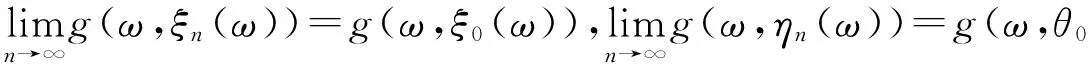
由g(ω，ξ0(ω))，g(ω，θ0(ω))是可测的，故可定义ξ(ω)=g(ω，ξ0(ω))，θ(ω)=g(ω，θ0(ω))，即有

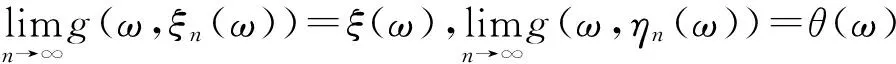
(12)

由(12)及g的连续性，

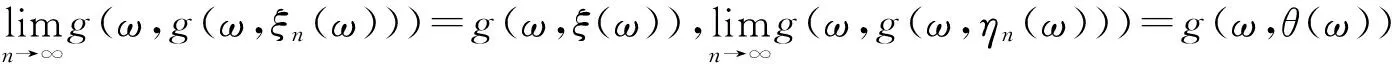
(13)

由F和g的可交换性有

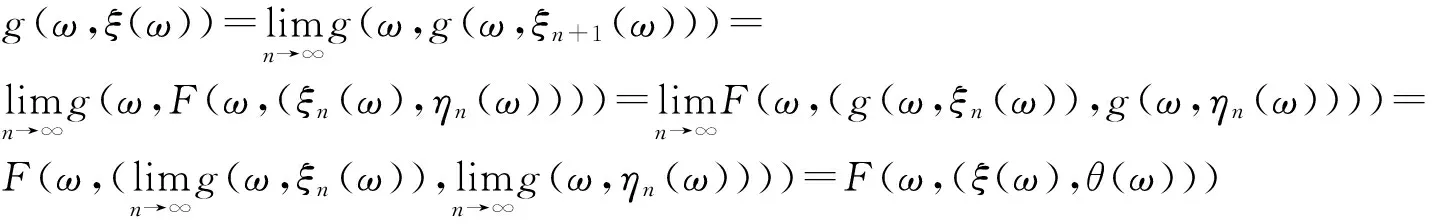
(14)

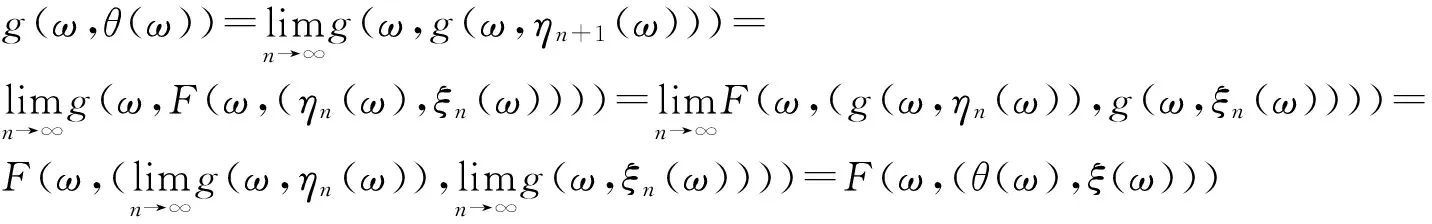
(15)

故F(ω×(ξ(ω)，θ(ω)))=g(ω，ξ(ω))，F(ω×(θ(ω)，ξ(ω)))=g(ω，θ(ω))，即(ξ(ω)，θ(ω))∈X×X是F和g的耦合随机重合点.

以下说明在(A6)的条件下，结论也成立.事实上，假设(A6)成立，由(A2)可知{g(ω，ξn(ω))}是非减的，且当g(ω，ξn(ω))→g(ω，ξ(ω))时，g(ω，ξn(ω))≤g(ω，ξ(ω))，n∈N.同时，由(A2)可知{g(ω，ηn(ω))}是非增的，且当g(ω，ηn(ω))→g(ω，θ(ω))时，有g(ω，ηn(ω))≥g(ω，θ(ω))，n∈N.由三角不等式，

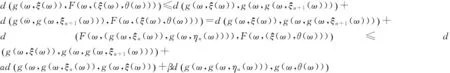
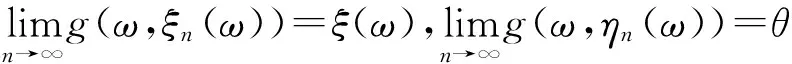
类似可证F(ω×(θ(ω)，ξ(ω)))=g(ω，θ(ω))，故(ξ(ω)，θ(ω))∈X×X是F和g耦合随机重合点.

定理2 设(X，≤)是一个偏序集，(X，d)是完备可分的度量空间，(Ω，Σ)是一个可测空间，F:Ω×(X×X)→X和g:Ω×X→X为混合单调算子.假设(A1)—(A6)成立，且对k∈(0，1)及所有满足x≤u，y≥v的x，y，u，v∈X，有

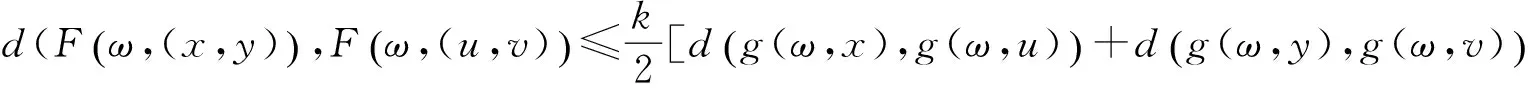
如果存在可测映射ξ0，η0∈X，使得ξ0(ω)≤F(ω，(ξ0(ω)，η0(ω)))，F(ω×(η0(ω)，ξ0(ω)))≤η0(ω)，则也存在可测映射ξ，θ:Ω→X，使得F(ω×(ξ(ω)，θ(ω)))=ξ(ω)，F(ω×(θ(ω)，ξ(ω)))=θ(ω)，∀ω∈Ω.即F和g存在耦合随机不动点点.

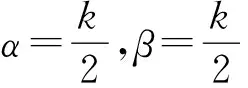
[1] GUO D J，LAKSHMIKANTHAM V. Nonlinear problems in abstract cone[M].New York：Academic Press，1988：267-275.

[2] GUO D J，LAKSHMIKANTHAM V. Coupled fixed points of nonlinear operators with application[J]. Nonlinear Analysis，1987，11(5):623-637.

[3] JIANG B H，XU S Y.Couple coincidence points for mixed monotone random operators in partially ordered metric space[J/OL].Abstract and Applied Analysis，2014[2014-12-12].http://dx.doi.org/10.1155/2014/484857.

[4] 王梓坤.随机泛函分析引论[J].数学进展，1962，5(1)：45-71.

[5] 郭大钧.非线性泛函分析[M].济南:山东科技出版社，1985:235-241.

[6] 梁瑛，吴宏锷.随机混合算子的耦合不动点定理[J].绵阳师范学院学报，2009，28(2):24-27.

[7] 李国祯，朱传喜.关于混合单调算子的耦合不动点定理[J].工程数学学报，1993，10(1):9-16.

[8] 许绍元.混合单调算子不动点存在唯一性定理及其应用[J].吉首大学学报(自然科学版)，2011，32(1)：11-13.

[9] 盛梅波.关于混合单调算子的新的不动点定理及应用[J].华东交通大学学报(理科版)，2003(5)：118-200.

(责任编辑：李亚军)

Couple coincidence points for mixed monotone random operators in partially ordered metric space

LI Cheng-geng，XU Shao-yuan，LIU Bo

(Department of Mathematics and Applied Mathematics，Hanshan Normal University，Chaozhou 521041，China)

Random mixed monotone operators in partially ordered metric spaces are considered. The results improve the problem of coincidence points for general monotone operators to mixed monotone random operators.

partially ordered;coupled coincidence points;mixed monotone operators； random operator

1000-1832(2016)04-0015-04

10.16163/j.cnki.22-1123/n.2016.04.004

2014-12-12

国家自然科学基金资助项目(10961003).

李承耕(1969—)，男，硕士，讲师，主要从事统计与非线性泛函研究；许绍元(1964—)，男，博士，教授，主要从事分行几何与非线性泛函研究；刘波(1977—)，男，硕士，讲师，主要从事统计与非线性泛函研究.

O 177.91 [学科代码] 110·67

A