高阶非线性代数微分方程组的亚纯允许解

金 瑾

(1.贵州工程应用技术学院数学系，贵州 毕节 551700；2.毕节循环经济研究院，贵州 毕节 551700)

高阶非线性代数微分方程组的亚纯允许解

金 瑾1，2

(1.贵州工程应用技术学院数学系，贵州 毕节 551700；2.毕节循环经济研究院，贵州 毕节 551700)

利用亚纯函数的Nevanlinna值分布理论，研究了高阶非线性代数微分方程组亚纯允许解的存在性问题，获得了微分方程组的亚纯解或同为允许的，或同为非允许的，进而得到了更一般的结果.

代数微分方程组；亚纯函数；允许解；Nevanlinna理论；值分布理论

1 预备知识

这里假设读者熟悉亚纯函数的Nevanlinna值分布理论的基本知识和通常记号.[1-20]关于微分方程组的允许解问题，有很多作者做了大量工作并得到一大批很好的结果.[1-10]

对下面的高阶非线性代数微分方程组

(1)

其中：

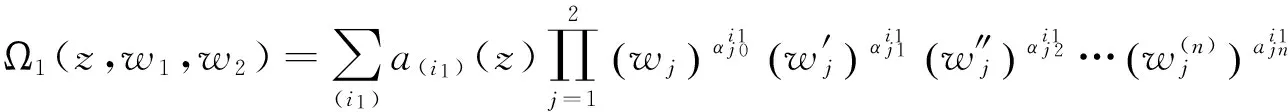
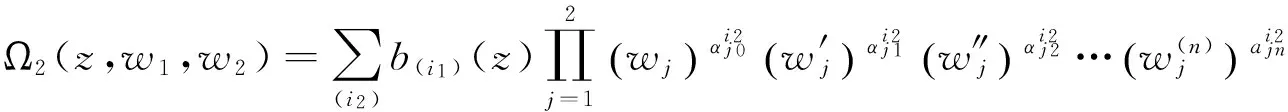
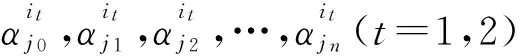
T(r，a(i1))=o(T(r，w1))，T(r，b(i2))=o(T(r，w2))，T(r，ai)=o(T(r，w1))，

T(r，bj)=o(T(r，w1))，T(r，ci)=o(T(r，w2))，T(r，dj)=o(T(r，w2)).

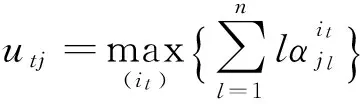
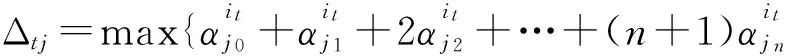
a11，a12，a21，a22为常数，则可知λtj≤utj≤Δtj.

定义1 设(w1，w2)是微分方程组(1)的亚纯解，S(r)为微分方程组(1)的所有系数的特征函数之和，即

S(r)=∑T(r，ai1)+∑T(r，bi2)+∑T(r，ai)+∑T(r，bj)+∑T(r，ci)+∑T(r，dj).

若(w1，w2)满足

S1(r)=o(T(r，w1))，S2(r)=o(T(r，w2))，r∉I1，

则称(w1，w2)为方程组(1)的亚纯允许解，其中I1是一个对数测度为有穷的例外值集.

定义2 设(w1，w2)是微分方程组(1)的亚纯解.若(w1，w2)中的分量w1，w2满足

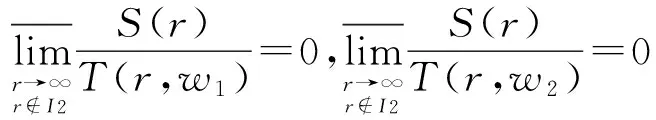
则称分量w1，w2为微分方程组(1)允许分量，其中I2是一个对数测度为有穷的例外值集.

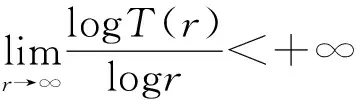
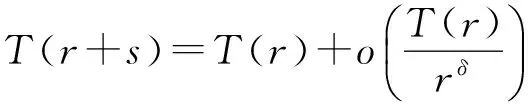
引理3 设aik(i=1，2；k=1，2)为非零常数，且

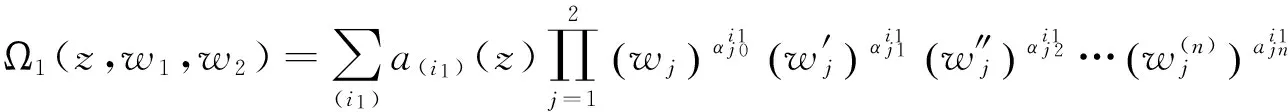
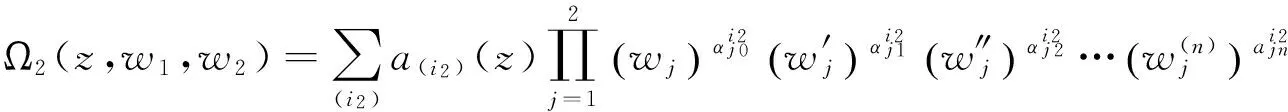
则

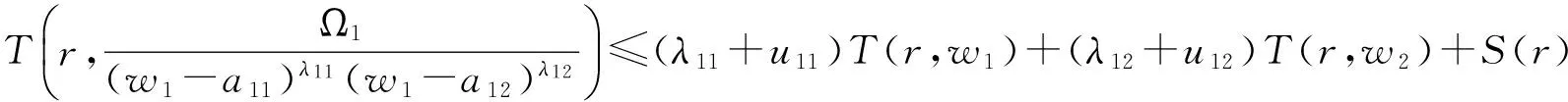
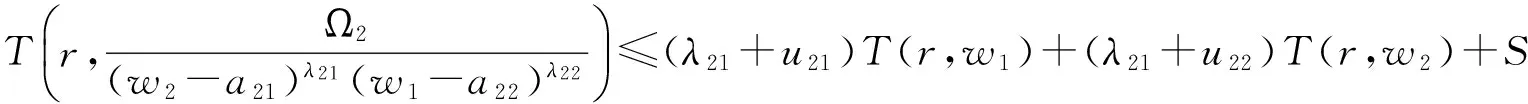
证明 因为

由文献[13]引理2得

(2)

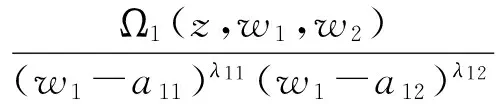
情形Ⅰ 若z0为Ω1(z，w1，w2)系数的极点，则

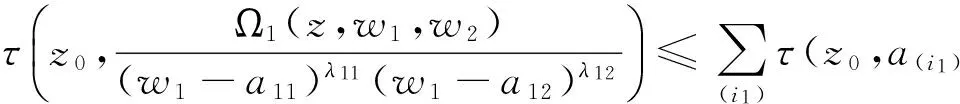
情形Ⅱ 若z0为wk的极点，则

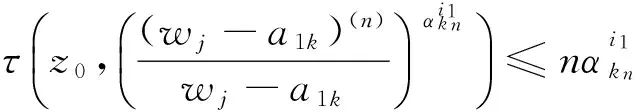
由此可得

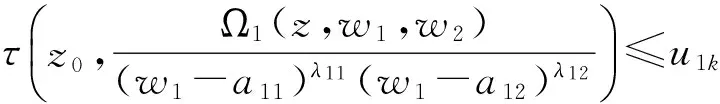
情形Ⅲ 若z0为wk-a1k的零点，但不是wk的极点，则

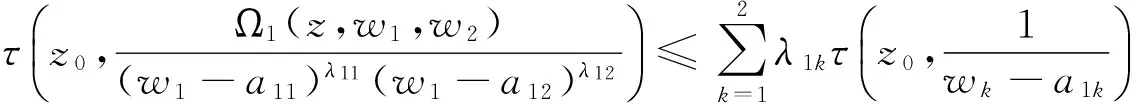
由上述三种情形得

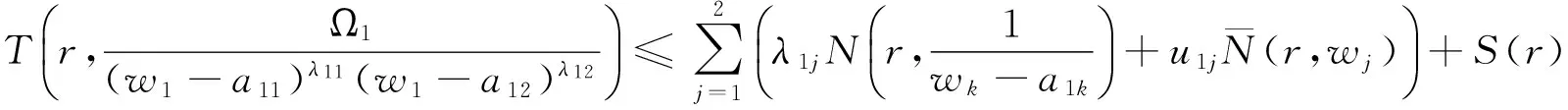
(3)

根据(2)—(3)式以及引理2得

故

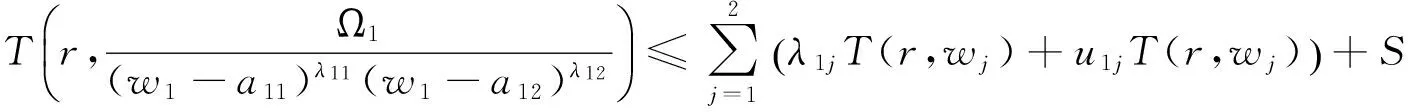
同理可得

即

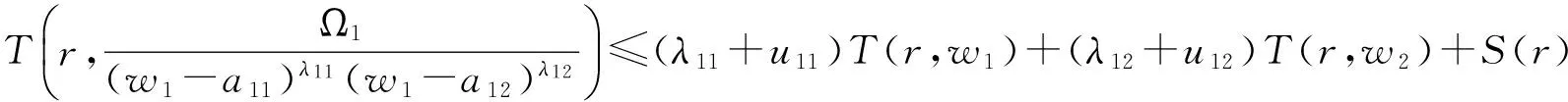
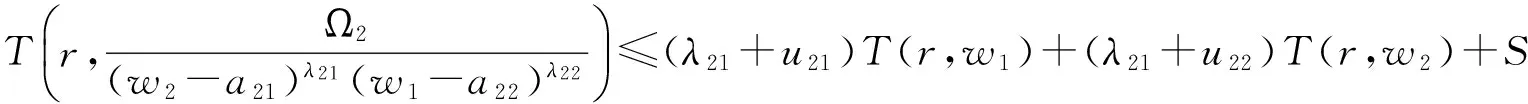
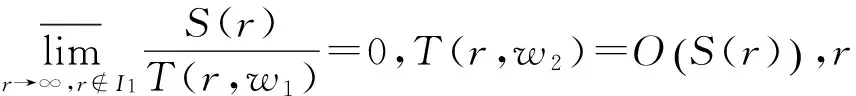
证明

其中I1和I2都是对数测度为有限的例外值集，故引理4成立.

2 主要结论

本文利用Nevanlinna值分布理论，对高阶非线性代数微分方程组(1)的亚纯允许解的存在性问题进行了研究.根据以上定义以及众多研究者研究结果的基础上，得到以下改进和推广的结论.

定理1 设(w1，w2)是非线性微分方程组(1)的有限级亚纯允许解，且

max{p1，q1}>λ11+u11，max{p2，q2}>λ22+u22.

则

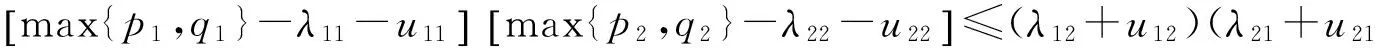
证明 由引理1可得

T(r，R1(z，w1))=max{p1，q1}T(r，w1)+S(r)，

(4)

T(r，R2(z，w2))=max{p2，q2}T(r，w2)+S(r).

(5)

由已知和引理3有

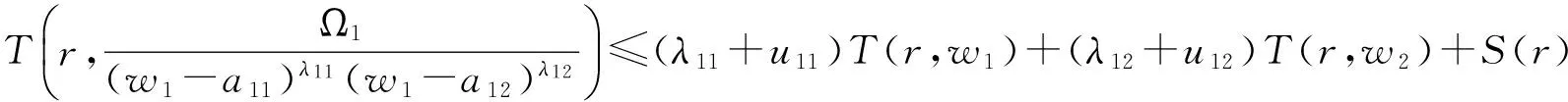
(6)

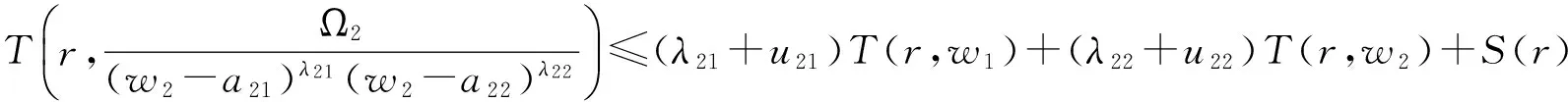
(7)

故由(4)—(7)式以及微分方程组(1)可得

max{p1，q1}T(r，w1)≤(λ11+u11)T(r，w1)+(λ12+u12)T(r，w2)+S(r)，

(8)

max{p2，q2}T(r，w2)≤(λ21+u21)T(r，w1)+(λ22+u22)T(r，w2)+S(r).

(9)

根据(8)—(9)式，

{max{p1，q1}-λ11-u11+o(1)}T(r，w1)≤(λ12+u12+0(1))T(r，w2)，

(10)

{max{p2，q2}-λ22-u22+o(1)}T(r，w2)≤(λ21+u21+o(1))T(r，w1)，

(11)

进而由(10)—(11)式即有

{max{p1，q1}-λ11-u11}{max{p2，q2}-λ22-u22}≤(λ12+u12)(λ21+u21).

定理2 设(w1，w2)是微分方程组(1)的有限级亚纯解，且max{p1，q1}>λ11+u11或 max{p2，q2}>λ22+u22.则(w1，w2)中的两个分量w1和w2或同为允许的，或同为非允许的.

证明 利用已知条件以及引理1与引理3结论可得

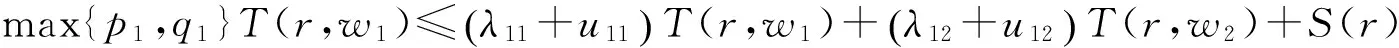
(12)

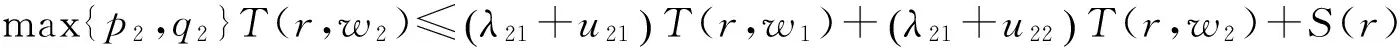
(13)

若分量w1为允许的，w2为非允许的，则(8)式变为

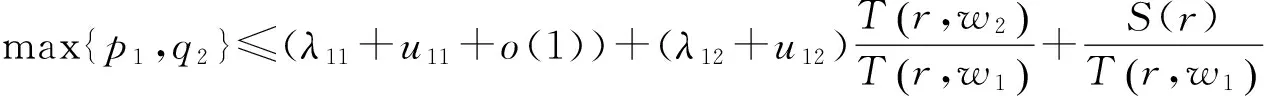
由引理4可知当r→∞时，除去一个对数测度为有限的例外值集外都有

max{p1，q1}≤λ11+u11.

这与定理2的已知条件矛盾.

若分量w2为允许的，w1为非允许的，则(9)式变为

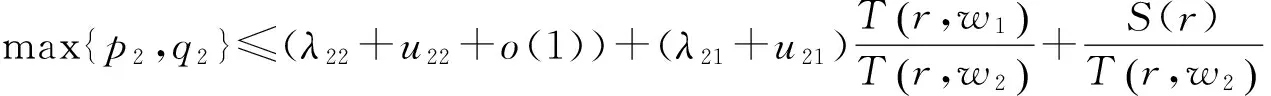
由引理4可知当r→∞时，除去一个对数测度为有限的例外值集外都有

max{p2，q2}≤λ22+u22.

这与定理2的已知矛盾.

综上，(w1，w2)中的两个分量w1和w2或同为允许的，或同为非允许的.

[2] 高凌云.复微分方程组m分量-可允许解[J].数学年刊，1997，18(2)：149-154.

[3] 高凌云.关于两类复微分方程组的允许解[J].数学学报，2000，43(1)：149-156.

[4] 高凌云.具有允许解的代数微分方程组的形式[J].系统科学与数学，2004，24(1)：96-101.

[5] 高凌云.代数微分方程组允许解的值分布[J].系统科学与数学，2007，27(4)：629-632.

[6] 高凌云.Malmquist型复差分方程组[J].数学学报，2012，55(2)：293-300.

[7] 王钥，高凌云.关于两类复非线性微分方程的代数体函数解[J].系统科学与数学，2013，33(2)：246-254.

[8] 高凌云.高阶差分方程解[J].数学学报，2013，56(4)：451-458.

[9] 吴桂荣.复域内代数微分方程组的允许解[J].福建师范大学学报(自然科学版)，1992，8(1)：16-20.

[10] 宋述刚.代数微分方程组的可允许解[J].数学杂志，2008，28(6)：685-688.

[11] LAINE I.Nevanlinna theory and complex differential equation [M].Berlin：Walter de Gruyter，1993：18-49.

[12] KORHONEN R.A new clunie type theorem for difference polynomials[J].Difference Equ Appl，2011，17(3)：387-400.

[13] 丁勇.一类微分方程组的非可允许分量[J].暨南大学学报，2013，34(1)：25-18.

[14] HILLE E.Ordinary differential equations in the complex domain[M].New York：Wiley，1976：1021-1028.

[15] 金瑾.关于一类高阶齐次线性微分方程解的增长性[J].中山大学学报，2013，52(1)：51-55.

[16] 金瑾.一类高阶齐次线性微分方程解的增长性[J].华中师范大学学报(自然科学版)，2013，47(1)：4-7.

[17] 金瑾.关于高阶线性微分方程解与其小函数的增长性[J].上海交通大学学报(自然科学版)，2013，47(7)：1155-1159.

[18] 金瑾.单位圆内高阶齐次线性微分方程解与小函数的关系[J].应用数学学报，2014，37(4)：254-264.

[19] 金瑾，武玲玲，樊艺.高阶非线性微分方程组的亚纯允许解[J].东北师大学报(自然科学版)，2015，47(1)：22-25.

[20] 金瑾.一类差分方程组的亚纯允许解[J].东北师大学报(自然科学版)，2016，48(2)：27-30.

(责任编辑：李亚军)

Meromorphic admissible solution of systems governed by higher order non-linear algebraic differential equations

JIN Jin1，2

(1.Department of Mathematics，Guizhou University of Engineering Science，Bijie 551700，China；

2.Research Institute of Circular Economy of Bijie，Bijie 551700，China)

Using Nevanlinna theory of the value distribution of meromorphic functions，the problem of the existence of meromorphic admissible solutions of complex higher-order nonlinear algebraic differential equation is investigated.It is obtained that the meromorphic solution of the differential equations system are all admissible or non admissible.Moreover，some other results are also given，which are more general than the previous ones.

algebraic differential equations systems；meromorphic function；admissible solution；Nevanlinna theory；value distribution

1000-1832(2016)04-0010-05

10.16163/j.cnki.22-1123/n.2016.04.003

2015-08-20

贵州省科学技术基金资助项目(2010GZ43286，2012GZ10526)；贵州省毕节市科研基金资助项目([2011]02)；贵州省教育厅重点项目([2015]392).

金瑾(1962-)，男，教授，主要从事复分析研究.

O 174.52 [学科代码] 110·41

A