三个自由度的机械臂运动优化模型
闫喜红
(太原师范学院 数学系,山西 晋中 030619)
三个自由度的机械臂运动优化模型
闫喜红
(太原师范学院 数学系,山西 晋中 030619)
随着高科技在生产、生活中的发展,机器人技术已经成为研究热点.多关节机械臂是机器人最重要的执行机构.文章主要针对具有三个转动节点的机械臂的运动进行.这种机械臂依靠节点的转动来移动机械爪从而达到抓取东西的目的.我们利用优化的思想及空间坐标转换对这种机械臂的运动在无障碍物和有障碍物的情况分别建立了数学模型.数值实验结果表明文章所建立的优化模型具有一定的实用性和有效性.
机械臂;最小二乘法;优化模型;障碍物
1 问题的背景
随着日益提高的工业自动化,工业生产和人民生活对机器人技术的需求越来越多.因此,机器人技术已经成为研究热点,并且也取得了好多成果[1-5].对机器人是由好多重要的部分组成.众所周知,机器人最重要的执行机构为机械臂.因此,研究机器人技术的首要任务就是研究机械臂,因此有很多学者专注研究机械臂[6-8].
1954年,美国联合控制公司研制出第一台机械臂,其结构为在机体上安装回转长臂,在其端部安装机械爪.随后二三十年,美国机械铸造公司和美国Uni-mate公司包括斯坦福大学和麻省理工学院等机构不断地研制改良机械臂,从而使得机械臂的技术更加成熟,比如,机械臂的动作更加丰富,操作误差越来要小.本文主要研究有三个节点的机械臂在单一的平面内的精确移动和搬运, 并且我们考虑两种不同的环境,一种是无障碍的环境,另一种是有障碍的环境.在无障碍的环境下,我们讨论了机械臂从一个给定的点移动到另外一个给定的点时,节点的最小转动方案.在有障碍的环境中,利用无障碍物环境下的结果,我们进一步对机械臂如何避开障碍物抓取东西进行了建模及模拟.
在机械臂的运动中,关节发挥着至关重要的作用.为了描述机械臂的运动轨迹,我们对每个关节设定了相应的参数,然后通过空间坐标转换的方法确定机械臂的定位.从出发点到目标点的运动过程,我们利用最小二乘方法建立了数学优化模型.对于有障碍物的情形,我们采用分段的方法把有障碍物的情形转化成无障碍物的情形的, 从而得到避开障碍物的运动方案. 我们所建立的模型为非线性规划,因此在求解时,我们采用解非线性规划常用的优化方法,例如最速下降法、牛顿法、信赖域法[9].
2 机械臂在无障碍物的平面内的运动
2.1 坐标变换
为了科学地分析机械臂在平面内的运动,第一步就是建立直角坐标系.设机械臂与操作台的连接节点为原点,以操作台所在的平面为准,x坐标轴为其水平方向所在的直线,y坐标轴为与操作台垂直的直线.为了方便,我们记机械臂的三个节点分别为O,A,B,终端的机械爪为C.如图1所示.我们称机械臂的每两个关节之间的器件为子机械臂.设从原点到端点的三条机械子臂的长度依次为l1,l2,l3.设θ1为子机械臂OA与水平线的夹角,θ2为子机械臂OA与子机械臂AB的夹角,θ3为子机械臂AB与子机械臂BC的夹角.图1给出了整个机械臂在坐标系中的示意图.
由图1及几何知识可得:A点坐标为(l1cosθ1,l1sinθ1).利用A点的坐标及AB的关系,可得B点的坐标为(l1cosθ1-l2cos(θ1+θ2),l1sinθ1-l2sin(θ1+θ2)),从而进一步求得C点坐标为(l1cosθ1-l2cos(θ1+θ2)+l3sin(θ1+θ2+θ3),l1sinθ1-l2sin(θ1+θ2)+l3cos(θ1+θ2+θ3)).

根据以上三个变换矩阵可得机械爪的位置C为:
从而可得
这里,r11=cos(θ1+θ2+θ3),r12=-sin(θ1+θ2+θ3),r14=l3cos(θ1+θ2+θ3)+l2cos(θ1+θ2)+l1cosθ1,r21=sin(θ1+θ2+θ3),r22=cos(θ1+θ2+θ3),r24=l3sin(θ1+θ2+θ3)+l2sin(θ1+θ2)+l1sinθ1,θ1+θ2+θ3是第三个子机械臂与x轴的夹角,r14是机械爪在x方向上的位移.r24是机械爪在y方向上的位移.根据以上的结论,就可以控制机械臂的运动.设目标点的坐标为(x,y). 则要求机械爪到达目标点(x,y)处时第三个子机械臂所在的直线在与x轴的夹角为φ,其在x轴的位移是x,在y轴的位移是y. 即,此时
由上面的分析可得如下方程组:
(1)
由方程组(1)可求得θ1,θ2,θ3,这里机械臂长度和初始点和终到点都是已知的,从而可得机械臂的运动方案.
2.2 模型建立


其中θi,1,θi,2,θi,3表示当机械臂末端的点C到达分段点(xi,yi)处时三个转动节点处所取的度数,θi,1,θi,2,θi,3与(xi,yi)满足(1),且
我们进一步考虑,在实际应用中,由于机械的一些物理性质,一般来说转动角不能过大或者过小.更进一步来说,转动得越大,消耗的能量也越多,而我们希望尽可能节约能量.为此, 我对模型1进行了改进,即在模型1的目标函数增加一项使得运动角度尽可能小,在约束条件加入对角度的限制.这样就建立以下改进的模型2.

其中,θi,1,θi,2,θi,3与(xi,yi)满足(1),且
θmin≤θi,1,θi,2,θi,3≤θmax.
这里θmin和θmax分别指节点处所能转动的最小角度和最大角度. 一般θmin取60度,θmax取120度.
为了刻画机械臂的运动,我们建立了模型1和模型2.但是这样的模型求解的难度很大.为了降低计算的难度,我们寻找更易求解且能刻画机械臂运动的模型.这个模型的基本思想是每次移动的过程中,在转动角度在一定范围内,找到一条最好的轨迹使得每次转动到达位置尽量接近每个分段点.从而对每个i小段建立下面的模型:
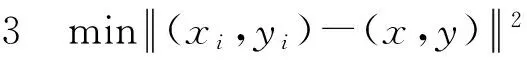
s.t.θi-Δ≤θi+1≤θi+Δ
其中,θi,1,θi,2,θi,3与(x,y)满足(1),且
其中Δ是指每次所能转动的最大角度.在实际问题中Δ一般取10度,(x,y)为在第i次转动的目标点.从模型3,我们可以看出求解模型3比求解模型1、模型2要简单很多.
2.3 模型求解
为了验证所建模型的实用性和有效性,我们把所建立的模型用于解决下面的实际问题,并且求解.在模型求解过程,我们使用MATLAB 7.0编写程序,并且利用函数命令Solve来求解方程组(1). 本试验所考虑机械臂结果为其三个子机械臂的长度分别为l1=l2=3单位长度,l3=2单位长度.初始点为(0,5),目标点为(5,5).在计算过程中我们取m=10.表1列出了相关的数值结果.

表1 无障碍物机械臂运动的关节转动角度的数值结果(弧度制)
从表1的数值结果显示了机械臂在每个时刻每个关节的转动情况,从而显示了机械臂的运动轨迹.
3 机械臂在有障碍物的平面内的运动
3.1 模型建立
在这一节中,我们研究机械臂在有障碍物的环境下的运动方案,即机械臂如何避开障碍物完成任务.不失一般性,我们假设在平面内有一开口容器,它由两条垂直边组成,其长度为h,并且与x轴的交点分别为a和b.我们的目的是要求机械臂从容器外M点取到物品移动到容器内的一点N.如图2所示.
首先,我们来具体分析这个问题.显然,和无障碍情况类似,首先需要找出机械臂从出发点到目标点的运动方案.因此,在这一个过程中,我们也采用把路线分割成小段,在每一小段控制恰当的转动角度. 与无障碍情况不同之处就是,在这个移动过程中机械臂要避开障碍物,即机械臂不能和障碍物想碰.从数学角度来看,就是机械臂的运动曲线方程和障碍物的表面方程不能相交.为了解决避开障碍物的问题,我们采用如下的方法,根据障碍物,我们首先用分段直线刻画机械臂将物品放入容器的过程,如图2,其中,实线条即为固定容器,虚线为运动轨迹的分段直线.

图2 有障碍物情形下的分段示意图
根据上面的分析,我们容易看出有障碍物情形与无障碍物情形的主要区别在于不允许机械臂碰撞到容器.因此我们把这种限制作为约束条件添加到模型1从而得到解决此问题的新模型.然而这样建立的模型求解很困难.为了解决计算困难的问题,我们希望建立计算复杂度较低的模型.为了避免机械臂与障碍物相撞,我们很容易想到首先要求机械爪的运动轨迹不能经过障碍物所在之处.这样,根据障碍物的形态,我们把运动轨迹设定为分段线段,并且每一段的任意一点都不会和障碍物所在之处的点相同.如图2, 我们把运动轨迹分为三段,每一段都不和容器相接触.这样机械爪所经过的路线就会避开和容器.其次,在运动过程也要避免每个子机械臂与障碍物相撞.因此,我们还得求出三个子机械臂在平面内分别所处的直线方程,使得这三个子机械臂所在的线段与障碍物所在的线段不相交,从而避免整个机械臂和容器相碰.在这样的思想下,我们在解决有障碍物的情形时,首先合理地确定分段线段为机械爪所移动的轨迹. 然后在每一段上,我们利用无障碍情形的模型确立如何运动.下面我们以图2给出的示意图建立优化模型.
基于图2的示例,我们建立有障碍物时机械臂的运动轨迹优化模型.首先我们进行合理的分段.从目标点N开始,我们把运动轨迹分为三段,分别为:第一段: 从目标点垂直向上建立一条线段,其另一个端点高于障碍物的最高点;第二段: 从第一段的末端点水平向原点方向移动,移动到障碍物左侧边界所在的直线上的点构成该线段;第三段: 连接第二段的末端和出发点所构成的线段.有了分段线段之后,分别对每一段利用机械臂无障碍物优化模型确立其运动方案.
注:以上的分段方法对于解决有障碍物的情形是可行的.也就是说,按照这个方法,我们总能找到一条路径使得机械臂能够避开障碍物实现取物和放物的操作.但是,此方法并不一定是最优的.
假设,容器壁长度为l,容器壁与x轴的交点分别(a,0)和(b,0),如图2所示.初始点为(x0,y0),目标点为(x′,y′),则分段线段中的三段线段分别为:

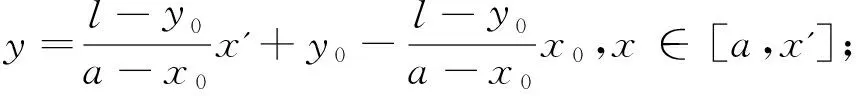

且设h1和h2分别为容器左侧壁以及右侧壁所在线段.根据模型1,对这三段分别建立无障碍的优化模型如下:
第一段关于转动角优化模型:

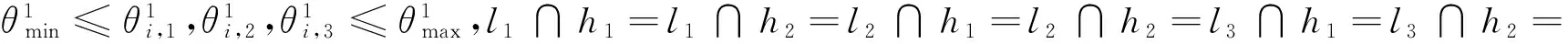
第二段关于转动角优化模型:


第三线段关于转动角优化模型:
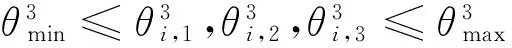

类似上一节,为了求解简单,借鉴模型3,建立更加简化的模型.三条线段简化的模型如下:
第一段简化模型:
s.t.

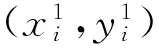
l1∩h1=l1∩h2=l2∩h1=l2∩h2=l3∩h1=l3∩h2=Ø;
轨迹二简化模型:
s.t.


l1∩h1=l1∩h2=l2∩h1=l2∩h2=l3∩h1=l3∩h2=Ø;
轨迹三简化模型:
s.t.


l1∩h1=l1∩h2=l2∩h1=l2∩h2=l3∩h1=l3∩h2=Ø;
其中,l1∩h1=l1∩h2=l2∩h1=l2∩h2=l3∩h1=l3∩h2=Ø可以用代数表达式表示出来.以第一段线段为例,需要满足:
3.2 模型求解
本节实验考虑的算例与第二节的算例类似.所考虑的三个子机械臂的长度和第二节算例中的相同.三个节点处的初始角都为90度.容器位于(1,0)与(4,0)处,容器壁高2单位长度.目标点为(3,0).机械爪的坐标为:(3cosθ1-3cos(θ1+θ2)+2sin(θ1+θ2+θ3),3sinθ1-3sin(θ1+θ2)+2cos(θ1+θ2+θ3)),且第一段就是
x=3,y∈[0,1].表2给出关于第一段的模型数值结果.
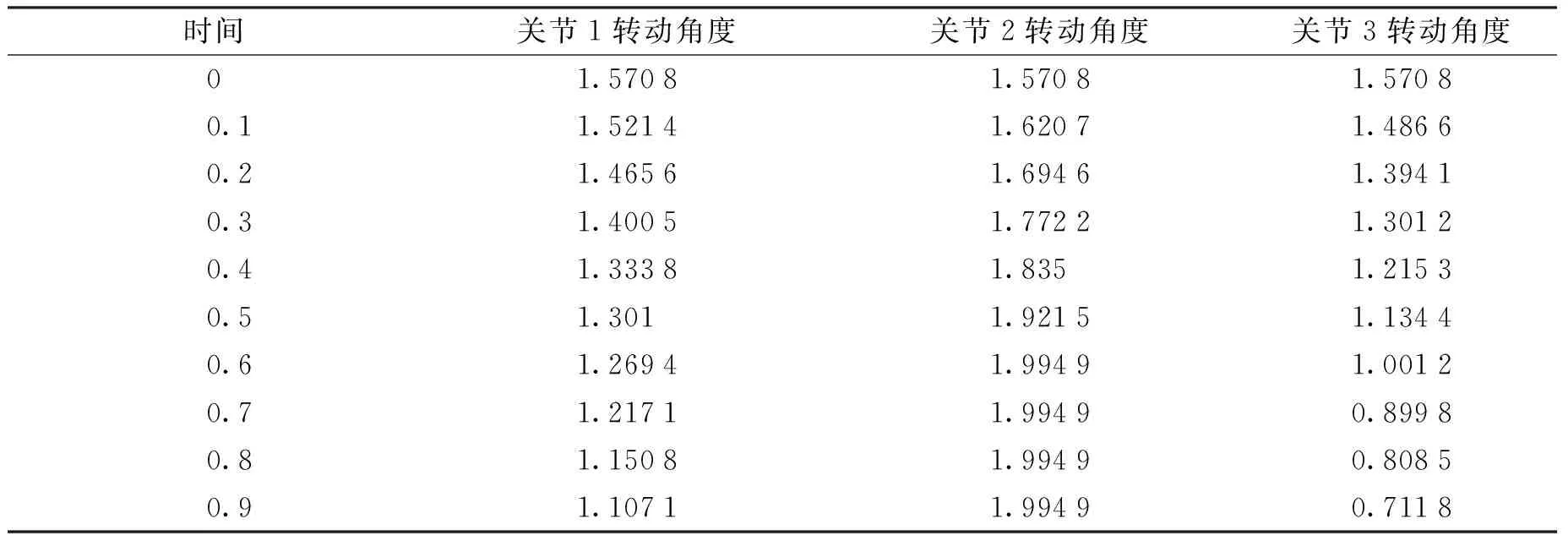
表2 第一段关节转动角度(弧度制)
同理,可得关于第二线段和第三线段机械臂的运动过程.
4 结论
本文研究了三自由度的机械臂在平面上的运动轨迹,并且考虑了两种状态,一种是无障碍物环境,另一种是有障碍物环境.对于第一种无障碍物环境,我们利用解析几何建立机械臂各个节点坐标之间的关系,从而确定机械爪的位置.并且,在此过程,我们利用矩阵的运算使得计算简单方便.有了坐标关系之后,我们采用逐点移动的方法,控制机械臂各个节点处的转动角从而让机械爪从出发点沿一定的曲线移动到目标点.对于有障碍物的情形,为了避开障碍物,我们根据障碍物建立分段直线,在每一段建立无障碍物模型,即把有障碍物的问题通过合理分段转换成无障碍物问题.数值结果验证了所建模型的实用性及有效性.
本文主要针对具有三个自由度的机械臂的运动. 实际的机械臂有更多的自由度.虽然我们的模型可以建立关于更多自由度机械臂的运动,但是计算量很大.这说明了我们模型的局限性. 对于有障碍物的情形,利用分段思想及无障碍物的优化模型来解决此问题.
但是这种方法建立的模型只是一种可行方案.建立最优的模型精确刻画机械臂的运动也是我们今后研究的主题之一.
[1] Francesco Chinello,Stefano Scheggi,Fabio Morbidi.KCT:A MATLAB toolbox for motion control of KUKA robot manipulators[C].Robotics and Automation(ICRA),2010 IEEE International Conference on Source,2010(58):4603-4608
[2] 罗家佳,胡国清.基于MATLAB的机器人运动仿真研究[J].厦门大学学报(自然科学版),2005(44):640-644
[3] John J Craig.机器人学导论[M].第3版.北京:机械工程出版社,2006
[4] 韩清凯,罗 忠.机械系统多体动力学分析、控制与仿真[M].北京:科学出版社,2010
[5] 沈红芳,宋又廉.基于ADAMS的弧焊机器人动力学仿真[J].机械设计与研究,2005(21):50-52
[6] 贾庆轩,陈 钢,孙汉旭,等.基于A~*算法的空间机械臂避障路径规划[J].机械工程学报,2010(46):109-115
[7] 陈鲁刚,平雪良,徐稀文.平面三自由度机械臂的轨迹规划及仿真[J].工具技术,2011(45):26-30
[8] 祁若龙,周维佳,王铁军.一种基于遗传算法的空间机械臂避障轨迹规划方法[J].机器人,2014(3):263-270
[9] 丁丽娟,程杞元.数值计算方法[M].第2版.北京:北京理工大学出版社,2005
Optimization Model about Design of Robotic Arms with Three Degrees of Freedom
YAN Xihong
(Department of Mathematics,Taiyuan Normal University, Jinzhong 030619, China)
With the development of high technology, Robotics technology gets more and more attention. Robotic arms play a core role in robots. This paper focuses on designing a primary robotic arm which consists of three rotation nodes rotating in a same plane. When operating, this robotic arm can move with the help of these three nodes. We design two models considering two different operation environments: without obstacles and with obstacles. Finally, the computational results show the model is applicable and effective.
robotic arm; least square method; optimization model; obstacles
2016-05-10
山西省自然科学基金(2014011006-1).
闫喜红(1980-),女,山西大同人,博士,太原师范学院数学系讲师,主要从事最优化方法与理论研究.
1672-2027(2016)02-0001-07
O212
A

