考虑客流量不确定性的客运专线开行方案鲁棒优化模型

孙惠娟，蔡仲启，彭春华

（华东交通大学电气与自动化工程学院，江西 南昌330013）

考虑客流量不确定性的客运专线开行方案鲁棒优化模型

孙惠娟，蔡仲启，彭春华

（华东交通大学电气与自动化工程学院，江西 南昌330013）

客流量的不确定性常会导致现有的客运专线开行方案难以满足列车运能约束条件而发生“弃流”，造成铁路部门运营效益流失。为了提高客运专线的整体运营效益和开行方案的鲁棒性，提出将可调节鲁棒优化理论引入到客运专线开行方案的优化制定中，考虑客流量的不确定性以及开行方案对客流的反馈影响，以区段客流运输量、区段与车站通过能力为约束，最大化铁路部门净收益为目标，构建了鲁棒性与经济性相协调的客运专线开行方案不确定区间可调节鲁棒优化模型。最后通过算例验证了模型的可行性与优越性，并对模型的鲁棒性和鲁棒代价等相关问题进行了深入分析。

客运专线；开行方案；客流量不确定性；可调节鲁棒优化

列车开行方案是铁路旅客运输组织的基础，现有铁路旅客列车开行方案的优化设计通常是基于确定的客流需求预测量来实现列车运营效益最大化[1]。然而，客运专线的客流量由于会受到天气环境、出行习惯、社会活动等诸多因素的影响，具有较大的随机性和波动性，目前还很难准确预测[2-4]。客流量的随机波动可能会使列车的运能约束发生违背而导致“弃流”（运输能力供不应求而造成客流损失），进而使铁路部门蒙受经济损失。

现有的对列车开行方案的研究主要采用确定性优化方法，考虑客流动态反馈控制、客流动态分配等，一般都没有考虑客流量不确定性的影响[4-5]。如在文献[5]中为反映列车开行方案对客流分配的反馈影响，建立了反映不同类型客流转化过程的客流动态分配模型，但由于是以事先预测的计划客流量制定开行方案，并未考虑客流量不确定性的影响，这样制定的开行方案对客流量的随机波动缺乏抗干扰能力（即鲁棒性），实际应用中可能会因客流量发生随机波动而使优化模型的约束违背，导致求得的开行方案失去优化意义。不确定性优化方法大致可分为：随机规划、模糊规划和鲁棒优化，它们分别采用随机变量、模糊变量和不确定集合对不确定性进行描述[6-7]。然而，随机规划中对实测数据进行统计分析后拟合得到的随机变量概率分布函数往往与实际情况存在一定程度上的偏差；模糊规划中由于数据样本有限及个人经验主观随意性等原因，想要客观准确地获取不确定性的概率分布函数或模糊隶属度函数并非易事。相较而言，鲁棒优化中获得不确定参数的集合则要容易得多，并能使求得的鲁棒最优解对于不确定参数在不确定集合内取任意元素时都能严格保证约束成立[8]。鲁棒优化是一种能够在不确定环境下兼顾鲁棒性和经济性的优化决策方法。文献[9]提出将鲁棒优化理论引入到含大规模光伏电站的电力系统优化调度中，建立了兼顾电力系统运行可靠性与经济性的鲁棒优化调度模型。文献[10]针对电梯群控调度过程中交通不确定的问题，提出一种电梯群控调度的鲁棒离散优化方法。文献[11]应用鲁棒优化方法对考虑风力发电机出力随机性的风电场最大装机容量进行优化。

为此，在考虑客流量不确定性的基础上，提出将鲁棒优化理论引入客运专线开行方案的制定中，以最大化铁路部门净收益为目标，结合开行方案对客流分配的反馈影响[5]，构建鲁棒性与经济性相协调的客运专线开行方案鲁棒优化模型。

1 现代鲁棒优化理论

式中：x为决策变量；ζ为不确定参数；U是用于描述ζ不确定性的不确定集合；m为约束条件个数。式中所示的不确定性优化问题往往难以直接求解，鲁棒优化关键是要通过某种方式将其进行等价转化或近似为确定性优化问题，这也是鲁棒优化的核心思想。

常规鲁棒优化方法为了保证约束条件在不确定变量取所有可能值时都能满足，其优化结果往往过于保守，甚至在极端情况下可能无解[9]。针对这一问题，Ben-Tal等人提出了更为灵活的可调节鲁棒优化方法[12]，将决策变量分为可调节变量和不可调节变量进行分阶段决策，有效地弥补了常规鲁棒优化过于保守的不足。但该方法一般需要多阶段求解，会大幅提高求解的复杂度。为降低求解的复杂度，Bertsimas等人进一步提出了不确定区间可调节鲁棒优化方法[13]。通过设置保守度或鲁棒性调节系数，对不确定参数的变化个数及范围进行控制，在实现鲁棒优化模型保守度可调节的同时，无须多阶段求解而不会增加求解的复杂度，且该方法还能适用于离散优化情形[14]。

基于上述分析，根据考虑客流量不确定性影响的客运专线开行方案优化问题的特点，本文将基于不确定区间可调节鲁棒优化理论，构建鲁棒性与经济性相协调的客运专线开行方案鲁棒优化模型，以提高开行方案的鲁棒性并实现运营收益的最大化。

现实中系统参数因受不确定性因素影响发生变化而导致系统原优化方案的性能急剧恶化甚至严重不可行的情形比比皆是[8]。作为解决不确定性优化问题的一种方法，鲁棒优化正是基于这一背景下提出的。鲁棒优化的数学描述如下[11]

2 模型建立

2.1 模型假设

本文中模型的建立基于以下4点假设[5]：

假设1：系统是封闭的。即系统状态只取决于系统内部影响因素，与外部因素无关。

假设2：客运专线列车可分为择站停高速（G型）、择站停中速（Z型）和站站停普速（L型）三种类型。乘客会根据开行方案选择适合自己的列车类型，组成不同类型的客流，分别称为G型客流、Z型客流和L型客流。

假设3：不考虑乘客中途换乘。

假设4：为了更贴合实际情况，本文将考虑不同开行方案对不同类型客流量产生的反馈影响，即各类型客流会受开行方案影响相互间会发生动态转化。根据乘客的通常意愿，可假定客流转化规律为：若新开行方案中G型列车在si站和sj站不停站，则si站到sj站的原先G型客流量将会优先选择转化为Z型客流，若Z型列车也不停靠si站和sj站，才会转化为L型客流。同理，原先Z型客流发生转化时会优先选择成为G型，然后才是L型。依此规律，各型列车的原先客流量在开行方案调整后会发生相互转化，最终形成各种开行方案所对应的实际客流量。

由上述假设，定义车站集S=（si│i=1，2，…，n），s1，s2，…，sn依次表示从始发站到终点站按经过顺序排列的车站；路段集E=（ei|i=1，2，…，n-1），ei为si和ei+1站间路段；列车类型集合T={G，Z，L}。

2.2 客流量的不确定区间模型

原先开行计划所对应的原先客流量的不确定区间模型为

2.3 约束条件

1）客流动态转化约束。由假设4，可得任意两站之间三种类型原先客流量经动态转化后的实际客流量计算公式为[5]

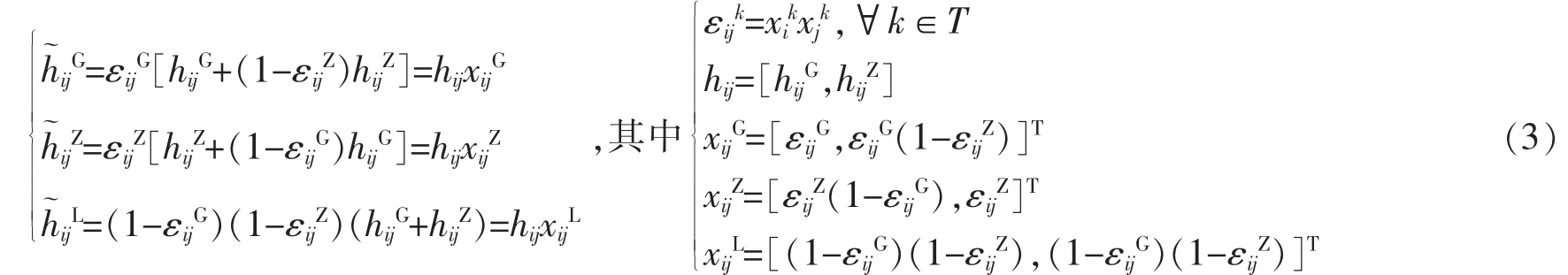
2）区段客流运输量约束。区段客流运输量不能超过其运输能力限制，即

3）区段通过能力约束。各区段上的运行列车数目不能大于其通过能力上限，令Le（ei）为区段ei的通过能力上限，即

4）车站通过能力约束。通过各车站的列车数目不能大于其通过能力上限，令Ls（si）为车站si的通过能力上限，即

5）

停站约束。由假设2可知，站站停普速列车有约束

此外，择站停高速和择站停中速列车在起始站与终点站必须停，即。

2.4 目标函数

式中：CI为铁路部门运营收益；n为客运专线车站总个数；dij为车站i，j之间的距离；pk为k型列车旅客公里票价率；分别为k型列车的车站停站费用，车公里费用，。这样既能保证当客流量在预设范围内波动时模型约束条件始终成立（不发生“弃流”），又能实现铁路部门的收益最大化，从而达到兼顾开行方案鲁棒性和经济性的目的。

3 模型求解

4 算例及分析

4.1 算例描述

为验证所建模型的有效性，构造如图1所示的客运专线网络。各区段的上方标注了该区段相应的编号和长度（km）[5]。区段的通过能力上限均取263对，始发站和终点站的通过能力上限取350对，中间站的通过能力上限取200对。模型其它基本参数如表1所示。

图1 城际客运专线路网图Fig.1 Network of intercity dedicated passenger lines

表1 模型参数Tab.1 Model parameters

4.2 模型的鲁棒性

1）常规优化模型下的开行方案。利用专门求解最优化问题的软件LINGO13.0对模型式（11）进行求解，取Γ=0，即为不考虑鲁棒性的常规优化模型，用黑色圆表示列车在该站停车，白色圆表示列车在该站不停车，可得常规优化模型下的开行方案如图2（a）所示，并作出该开行方案下各型列车的运能约束如图3（a）（图中横坐标为）所示。由图3（a）可知，当不考虑鲁棒性时，G、Z型列车均存在运能约束违背风险（图中实线与虚线的交点即为运能约束违背临界点）。大约当时，G型列车运能约束违背，发生“弃流”；大约当时，Z型列车运能约束违背，发生“弃流”。可见，标称模型下求得的开行方案鲁棒性差，不能有效适应客流量发生波动的情形。

2）鲁棒优化模型下的开行方案。若取Γ=5，即考虑最强鲁棒性，可得鲁棒优化模型下的开行方案如图2（b）所示，并可作出该开行方案下各型列车的运能约束如图3（b）所示。如图3（b）可知，当不考虑鲁棒性时，G、Z、L型列车均不存在运能约束违背风险（因为图中实线与虚线不存在任何交点）。可见，鲁棒优化模型下求得的开行方案鲁棒性好，可以很好地适应客流量发生波动的情形，即当受到不确定性影响，在内发生任意波动时，对比上述常规优化模型下的开行方案，鲁棒开行方案可以使各型列车的运能约束始终保持成立，不会发生“弃流”现象。

图2 开行方案对比Fig.2 Comparison of passenger train plans

图3 列车运能约束情况对比Fig.3 Comparison of transportation capability constraints

4.3 鲁棒代价

表2 鲁棒最优解Tab.2 Robust optimal solutions

表2中，运营收益损失是以不考虑鲁棒性情形下的运营收益658 920.1（元）作为比较基准计算得出的。由表2数据结果，可得到γ、Γ与运营收益三者的关系：

1）对比表2中Γ取不同值的情况可知，当γ一定时，运营收益与Γ成反比。Γ越大，原先客流量矩阵hk中不确定参数的可变化个数越多，鲁棒优化模型考虑的不确定性影响因素越多，提供的约束保护越强（即模型的鲁棒性越强），运营收益越小（即所需付出的“鲁棒代价”越大）。对表2中γ=0.04及γ=0.05进行表内数据对比也可得出一致的结论。

2）对比表2中γ取不同值的情况可知，当Γ一定时，运营收益与γ亦成反比。γ越大，不确定客流量的允许波动范围越大，鲁棒优化模型所提供的约束保护越强（即模型的鲁棒性越强），运营收益越小（即所需付出的“鲁棒代价”越大）。

综上所述，在鲁棒优化的现实应用中，必须根据实际情况对模型的鲁棒性和经济性作出适当的取舍抉择。过分追求模型的鲁棒性会大大削减经济性，严重时可能会使运营收益过低而使优化本身失去意义；反之，过分追求经济性则可能会使模型的抗干扰能力脆弱，导致系统不能安全稳定运行。如表2所示，若是过分注重模型的鲁棒性，取γ=0.5，Γ=5，则运营收益损失百分比将达到13.22%，这将使模型的经济性承受较严重的损失；而若取γ=0.02，Γ=1，则运营收益损失百分比虽然只有1.06%，但模型的保护范围过小，以致客流量即便只发生微小的波动，都有可能使得模型约束发生违背而导致“弃流”。如果客观要求运营收益损失不得大于10%，为了同时兼顾系统运行的鲁棒性和经济性，取γ=0.04，Γ=2，情形下对应的鲁棒优化开行方案应是较好的选择。

5 结束语

基于不确定区间可调节鲁棒优化理论，考虑客运专线客流量不确定性的影响，构建了鲁棒性与经济性相协调的客运专线开行方案可调节鲁棒优化模型，并成功将其转化为鲁棒对等式进行了有效求解。算例应用结果充分表明了该模型在抵抗不确定性干扰方面的优势及鲁棒性所需付出的代价。通过对鲁棒优化问题在鲁棒性和经济性上的博弈关系分析，提出了一种在实际应用中兼顾模型鲁棒性与经济性的抉择方法，为客运专线开行方案优化问题提供了新思路。

考虑到乘客换乘、选乘等问题的复杂性，所建立的鲁棒优化模型还有待进一步完善。此外，也可在本文的基础上考虑多目标鲁棒优化等更复杂的模型，以使客运专线开行方案满足更为全面丰富的需求。

参考文献：

[1]史峰，周文梁，陈彦，等.基于弹性需求的旅客列车开行方案优化研究[J].铁道学报，2008，30（3）：1-6.

[2]李倩.基于路网的高速铁路客流预测方法研究[D].北京：北京交通大学，2011.

[3]骆晨.基于多次修正残差灰色模型的铁路客流预测[J].华东交通大学学报，2013，30（4）：19-23.

[4]陶思宇，李美彦.基于客流动态反馈控制的客运专线旅客列车开行方案调整方法[J].铁道运输与经济，2012，34（10）：20-25.

[5]彭宏勤，朱郁俊.基于客流动态分配的城际列车开行方案[J].交通运输系统工程与信息，2013，13（1）：111-117.

[6]梅生伟，郭文涛，王莹莹，等.一类电力系统鲁棒优化问题的博弈模型及应用实例[J].中国电机工程学报，2013，33（19）：47-56.

[7]刘宝旋，赵瑞清.随机规划与模糊规划[M].北京：清华大学出版社，1998：37-222.

[8]BEN-TAL A，NEMIROVSKI A.Robust optimization methodology and applications[J].Mathematical Programming，2002，92（3）：453-480.

[9]彭春华，谢鹏，陈臣，等.大规模光伏电站接入电网可调节鲁棒优化调度[J].中国电机工程学报，2014，34（25）：4324-4332.

[10]宗群，窦立谦，王维佳.电梯群控系统的一种鲁棒离散优化调度策略[J].控制与决策，2008，23（5）：520-524.

[11]李斯，周任军，童小娇，等.基于盒式集合鲁棒优化的风电并网最大装机容量[J].电网技术，2011，35（12）：208-213.

[12]BEN-TAL A，GORYASHKO A，GUSLITZER E，et al.Adjustable robust solutions of uncertain linear programs[J].Mathematical Programming，2004，99（2）：351－376.

[13]BERTSIMAS D，SIM M.The price of robustness[J].Operations Research，2003，52（1）：35-53.

[14]BERTSIMAS D，SIM M.Robust discrete optimization and network flows[J].Mathematical Programming，2003，98（1/3）：49-71.

[15]陈宝林.最优化理论与算法[M].北京：清华大学出版社，2005：234-238.

[16]吴昌进.昌九城际轨道交通运量预测及运输方案研究[D].北京：清华大学，2008：26-55.

Robust Optimal Model of Train Plans for Passenger Dedicated Lines in View of Uncertainty of Passenger Flow

Sun Huijuan，Cai Zhongqi，Peng Chunhua
（School of Electrical and Automation Engineering，East China Jiaotong University，Nanchang 330013，China）

The uncertainty of traffic flow often makes the present train plans for dedicated passenger traffic lines cannot meet train capacity constraints,which results in traffic flow loss and operation benefit loss of railway department.To enhance the overall operation benefit of dedicated passenger traffic lines and the robustness of train plans,with the application of adjustable robust optimization theory for optimization of train plans,considering the uncertainty of passenger flow and the response of train plans on passenger flow,setting passenger traffic volume of railway section,railway section and station carrying capacity as constraints and the maximal net income of railway department as objective,this paper establishes the adjustable robust optimization model in uncertain intervals of train plans for dedicated lines,which coordinates robustness and economy.Finally,the model’s feasibility and superiority are verified by a calculation example,and the robustness and the price of robustness are further analyzed.

passenger dedicated lines；train plans；uncertainty of passenger flow；adjustable robust optimization

TP13；U292

A

1005-0523（2016）06-0083-08

（责任编辑 姜红贵）

2016－06－28

国家自然科学基金项目（51567007）；教育部人文社科青年基金项目（14YJCZH135）；江西省科技支撑计划项目（20142BBE50001）；江西省自然科学基金项目（20152ACB20017）；华东交通大学校立科研基金项目（15DQ03）

孙惠娟（1982—），女，讲师，研究方向为复杂系统优化研究。