乘性噪声诱导复杂系统阵列信噪比增益

冯天荃,易 鸣

（1.南京师范大学教师教育学院，江苏 南京210023；2.华中农业大学理学院，湖北 武汉430070）

乘性噪声诱导复杂系统阵列信噪比增益

冯天荃1,易 鸣2

（1.南京师范大学教师教育学院，江苏 南京210023；2.华中农业大学理学院，湖北 武汉430070）

研究一类并联非耦合双稳振子阵列信号处理中输入的加性噪声及彼此独立的阵列各子系统内部乘性噪声驱动下的随机共振现象。通过数值模拟，证明了当阵列数目增加到一定数目时，系统的乘性阵列噪声将使得信噪比增益大于1，而且阵列数目越大，信噪比增益区间越大。通过对该系统的极限均值函数和稳态相关函数的数值模拟，证明了阵列乘性噪声诱导的任意两个独立的双稳振子的统计行为能直接反映该系统中信噪比增益特性。研究结果不仅将拓展非线性动力学系统阵列信号处理理论，也将为噪声诱导复杂系统及复杂网络中随机动力学行为研究提供一种新的思路。

阵列随机共振；信噪比；双稳系统；乘性阵列噪声

随机共振(stochastic resonance，SR)的概念最初于关于地球冰期回归的研究中提出[1-2]。几十年来，随机共振现象引起了包括物理学、生物学、神经科学和信号处理等学科领域研究者的广泛关注。人们一般采用信噪比来分析随机共振现象。信噪比增益大于1的区域是当前复杂系统随机动力学研究及相关应用方面的热点研究课题[3-7]。对于线性系统，一般信噪比的增益为1。在不适用线性响应理论的体系，已有的研究表明信噪比增益大于1的情况是存在的，比如，阈值比较器或传感器组成的并联阵列以及一些非线性动力学系统已观察到阵列随机共振现象。

大多数之前的阵列随机共振研究包含特定的非线性，通过将非线性系统组合成阵列，调整噪声和信号幅值，已观察到阵列随机共振效应。比如，考虑任意可调节静态非线性时，对于添加白噪声的弱周期信号通过局部最优非线性能够达到最大的信噪比增益，而且此时的信噪比增益超过1。文献[8]在双稳振子的并联耦合阵列系统中考虑亚阈值正弦信号驱动包含噪声的双稳子系统发现了信噪比增益大于1的现象。然而，该研究假设每个双稳子系统仅受一个净正弦信号驱动，仅仅考虑了输入信号的噪声效应。而在实际情况下，输入信号在到达双稳并联阵列的传播路径中也应该考虑噪声效应。

基于一类包含输入噪声的周期信号驱动的双稳振子的并联非耦合动态阵列，本文研究了输出信噪比增益及优化问题。与前述研究不同的是，本文考虑每个双稳子系统都同时受到内部乘性噪声。本文证明了输出信噪比随双稳子系统内部乘性噪声强度的增加呈现先单调增加的现象，而在内部乘性噪声强度达到某一特定值时，输出信噪比达到最大，然后随着噪声强度继续增加，信噪比的输出呈现缓慢下降。更重要的是，当双稳并联非耦合阵列数目增大到一定值时，系统的乘性阵列噪声将使得信噪比增益大于1，而且阵列数目越大，信噪比增益区间越大，无限并联阵列的最大信噪比增益可达到全局最优值。

1 模型与方程

考虑并联非耦合双稳态振子阵列模型，该阵列模型由N个并联非耦合双稳振子组成，每个双稳振子的输入都是受相同的正弦信号加噪声的混合信号s（t）+η（t）。其中，s（t）=Asin（2πt/Ts）是一个周期为Ts、幅值为A的确定性的正弦信号，η（t）是零均值高斯白噪声，不受s（t）的约束，并且自关联函数为（[η（t）η（0）]＝Dηδ（t）（Dη表示噪声强度）。同时，每个双稳振子的内部乘性噪声ξi（t）（i=1，2，…，N）与输入的混合信号s（t）+η（t）无关联。N个双稳振子阵列内部乘性噪声项ξi（t）是相互独立的，其自关联函数为[ξ（t）ξ（0）]=Dξδ（t）（Dξ为噪声强度）[9-14]。阵列中双稳振子的内部状态xi（t）可以通过郎之万方程来描述：

其中：i=1，2，…，N；τa和xb为双稳子系统的实参数。阵列的输出设为这些双稳子系统的输出xi（t）的算术平均值，即

由于参数τa和xb分别具有时间和幅值的量纲，需要将方程（1）进行无量纲化。假设xi（t）＝xi（t）／xb，A=A／xb，t=t／τa，Ts＝Ts／τa，Dη＝Dη／（τax2b）和Dξ＝Dξ／（τax2b），方程（1）可以被改写为下面的无量纲化形式，即

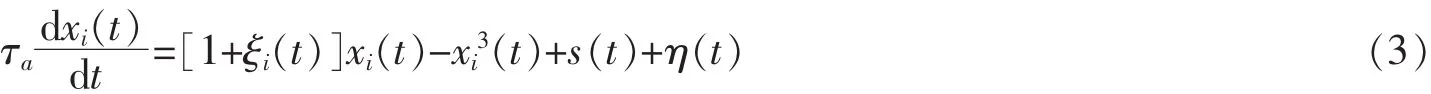
需要注意的是，如果输入信号s（t）的无量纲幅值满足，则输入信号s（t）是亚阈值信号，否则，s（t）是超阈值信号。通常情况下，阵列的求和输出响应是一个随机信号。但是，如果s（t）是周期为Ts的周期性输入信号，那么，输出y（t）一般是一个具有相同的周期Ts的稳态随机信号。为了研究并联非耦合双稳态振子阵列系统的输入－输出反应，本文将利用Euler-Maruyama离散数值方法求解方程（3），且数值求解过程中的采样时间步长δt远小于周期Ts。根据广义的输入－输出理论[9]，在任意时间t，阵列的求和响应y（t）可以表示为它的非稳态平均值E［y（t）］加上统计扰动之和，即。这里的非稳态平均值具有n阶傅里叶系数

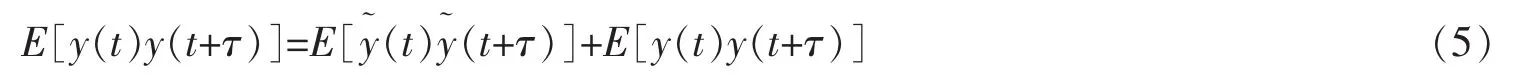
根据方程（5），可以得到稳态自关联函数Ryy（τ）

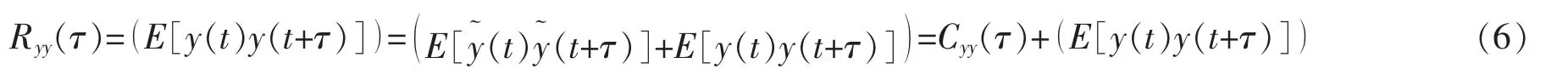
其中，Cyy（τ）为稳态自协方差函数。功率谱密度Ryy（v）是自关联函数Ryy（τ）的傅里叶变换

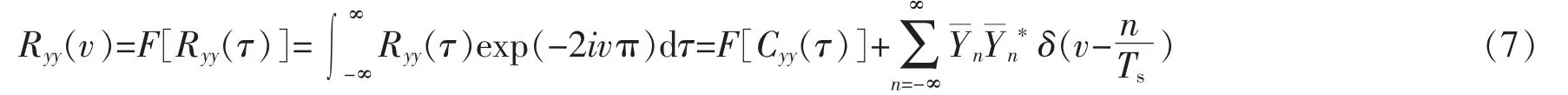
从方程（7）可以看出功率谱密度Pyy（v）由相干频率为n＝Ts幅值为的频谱构成，叠加到Cyy（τ）的傅立叶变换表示的宽带背景噪声中。需要指出的是，表示［y（t）］的非稳态方差，Cyy（0）＝（var［y（t）］）为阵列输出y（t）的稳态方差。稳态自协方差函数Cyy（τ）可以表示为

其中，h（τ）为互关联系数，且其傅里叶变换为F［h（τ）］＝H（v）。这样，方程（7）的功率谱密度可以改写为

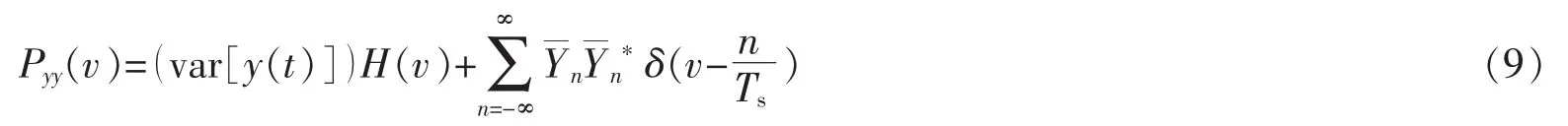
阵列输出信噪比被定义为谱线1/Ts上的功率与以频率1/Ts为中心的附近频带ΔB内的噪声功率之比，即

以同样的方法，可以得到周期性信号加噪声的混合信号s（t）+η（t）的输入信噪比

其中，ση为高斯噪声η（t）的均方根。根据方程（10）和（11），可以得到并联非耦合双稳阵列的信噪比增益，即

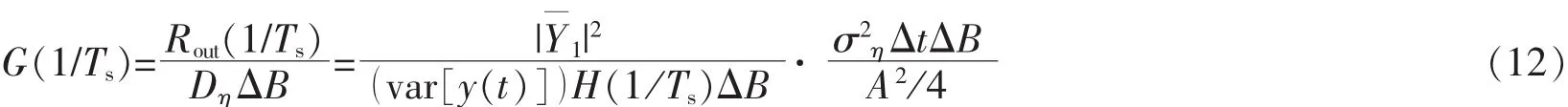
基于方程（10）－（12），本文将通过双稳阵列各子系统及阵列噪声的调控，详尽分析并联非耦合双稳阵列的信噪比及信噪比增益性质。如果该阵列的信噪比增益G（1/Ts）大于1，则说明双稳子系统阵列和阵列噪声的相互作用是一种潜在可靠的控制阵列信号的方法。

2 阵列随机共振和信噪比增益的计算结果

本文已经推导得到了系统的输入、输出信噪比Rin（1/Ts），Rout（1/Ts）及信噪比增益G（1/Ts）的精确表达式。值得指出的是，本文考虑了该阵列系统同时受到两种不同的噪声的作用，即输入的外部加性噪声η（t）以及每个子系统彼此独立的内部乘性噪声ξi（t）。这一点不同于前人的研究[8]。在本文中，信噪比及信噪比增益会受到输入的外部加性噪声及子系统内部乘性噪声的共同影响。

首先，考虑单个双稳振子的情况，即选取并联非耦合双稳振子阵列大小为N=1，则对应的输出。考虑输入信号是一个振幅为A＝0.5，频率1/Ts的正弦信号并包含输入噪声η（t），图1（a）和1（b）分别绘出了输出均值E［y（t）］和稳态自协方差函数Cyy（τ）的时间演化曲线。图1（a）和1（b）均选取了不同的输入噪声强度值，即，ση＝0.5（实线），ση＝1.2（虚线），ση＝2（点线）和ση＝3（点-虚线）。从图1（a）可以看出：随着噪声强度ση的增加，周期性输出均值E［y（t）］有一个相同的频率1/Ts＝0.01，输出均值E［y（t）］的最大振幅出现在输入外部噪声强度为ση＝1.2的位置。此外，从图1（b）的稳态自协方差函数Cyy（τ）可以看出：随着输入噪声强度ση从0.5增加到3，关联时间τ从72逐步减小到18。但是，稳态方差Cyy（0）=（var［y（t）］）表现出非单调特性，即随着输入外部噪声强度ση从0.5，1.2，2增加到3，稳态方差Cyy（0）分别对应为0.394，0.323，0.405和0.781。根据图1的结果，结合输入、输出信噪比Rin（1/Ts）的精确表达式，通过简单的计算就能得到系统存在典型的阵列随机共振现象，这一结果与已有的研究结果是一致的[8]。此外，从信噪比增益G（1/Ts）的表达式也能看出，信噪比增益G（1/Ts）是小于1的。实际上，只要输入的正弦信号的振幅A是亚阈值或稍微超阈值[3]，都不会出现信噪比增益，即G（1/Ts）＜1。但是，当输入的正弦信号的振幅A增加到一个更大的值时，在一定的噪声水平下，才可能实现信噪比增益[3]。

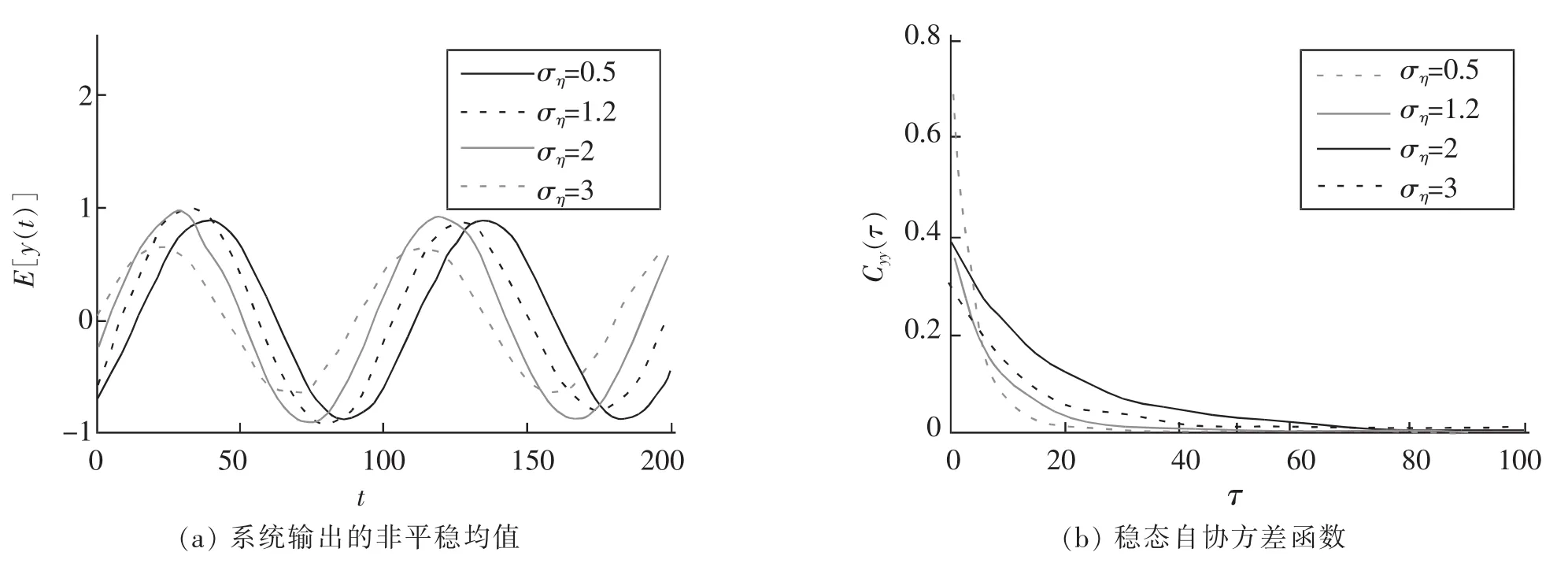
图1 阵列系统输出特性Fig.1 The output properties of the array

接下来，研究并联非耦合双稳振子阵列大小满足N≥2时的信噪比及信噪比增益性质。考虑输入的加性噪声强度值为ση＝1.9，对输入亚阈值信号（A=0.34）及超阈值信号（A=1）两种不同的条件，图2绘出了并联非耦合双稳动态阵列的信噪比增益G（1/Ts）随阵列内部乘性噪声ξi（t）强度σξ的变化曲线。图2（a）-（b）分别选取了不同的输入信号幅值和输入信噪比，即图2（a）A=0.34，Rin=8.89；图2（b）A=1，Rin=76.2。从图2可以看出，当阵列数目N达到一定值时，阵列的信噪比增益G（1/Ts）随阵列内部乘性噪声强度σξ的变化展示为非单调曲线，该类现象是典型的“阵列随机共振”现象[9]。而且，图3的结果也表明，信噪比增益大于1的结果（即G（1/Ts）＞1）不仅在超阈值信号输入时（即A=1）出现，而且在亚阈值信号情况（即A=0.34）时也能有效观察到G（1/Ts）＞1的现象。更重要的是，图2也证明了信噪比增益大于1的参数区间随着阵列数目的增加而扩展，而且，随着输入信号幅值A的增大，对于同等大小的阵列数目N，信噪比增益G（1/Ts）能达到一个更大的局域最大值。例如，从图2（a）和图2（b）的比较，可以看出在阵列大小同为N＝100的情况，信号幅值为A= 0.34时的信噪比增益G（1/Ts）要比信号幅值为A=1时的要小。研究结果表明了阵列随机共振与前面所介绍的随机共振理论[8]不同之处。前人的研究[8]假设了每个双稳子系统仅受一个净正弦信号驱动，仅仅考虑了输入信号的噪声效应，其随机共振的机制归因于输入信号中的加性噪声。而本文中的随机共振是由每个双稳子系统中的乘性噪声诱导的双稳阵列的集振非线性反应。同时，在某些情况下，可以通过调谐内部乘性噪声ξi（t）的强度，使得阵列输出处于最佳工作区域，即G（1/Ts）＞1的区域，这是阵列信号处理中一个很有意义的结果。图2已经证明了阵列信噪比增益G（1/Ts）随阵列数目的增加局部最大值会相应增加，且对应的最优化的内部乘性噪声强度σξ向右偏移；因此，研究阵列数目N→∞时的阵列信噪比增益G（1/Ts）的全局最大值是极有意义的。

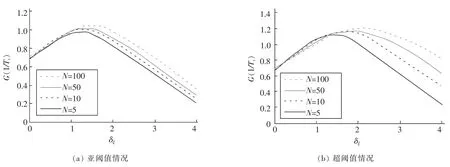
图2 阵列信噪比增益随阵列内部乘性噪声强度的变化曲线Fig.2 The array SNR gain as a function of the amplitude of array noise

在t时刻如果阵列数目N→∞，可以通过稳态自关联函数和稳态自协方差函数极限来进一步分析阵列的信噪比增益性质。在任意时刻t，稳态自关联函数和稳态自协方差函数极限表示为

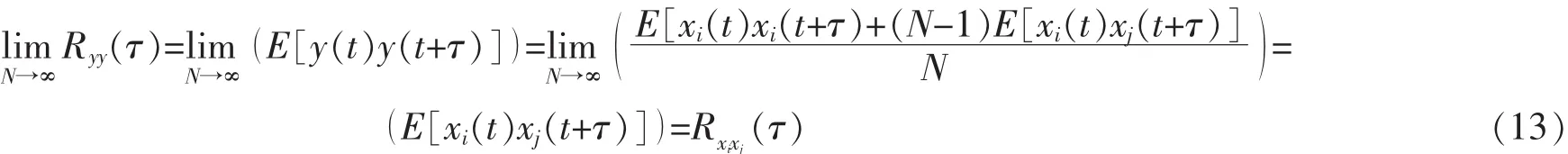
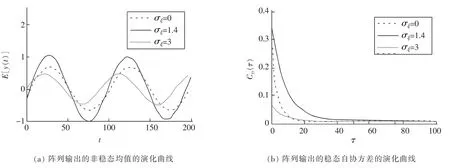
图3 阵列系统输出特性Fig.3 The output properties of the array

其中，方程（13）和（14）中的下标满足i≠j，i，j＝1，2，…，N；因此，可以利用任意两个相互独立内部乘性噪声ξi（t）和ξj（t）中的双稳态振子来代替阵列数目趋于无穷大（N→∞）的情况来计算阵列的信噪比增益G（1/Ts）。图3（a）绘出了阵列数目N→∞时内部乘性噪声强度σξ取不同值时输出y（t）的非稳态均值E［y（t）］的演化曲线。图3（b）绘出了对应于图3(a)的输出y（t）对应的稳态自协方差函数Cyy（τ）的演化曲线。图3（a）和图3（b）中不同的内部乘性噪声强度σξ＝0，1.4，3分别用实线，虚线和点线来表示。本文采用了文献[9]中的数值方法，选取频带ΔB＝1/Ts，采样时间Δt=0.001／ΔB。这样，可以依据非稳态均值E［y（t）］和稳态自协方差函数Cyy（τ）分析阵列输出的信噪比Rout（1/Ts）及信噪比增益G（1/Ts）。

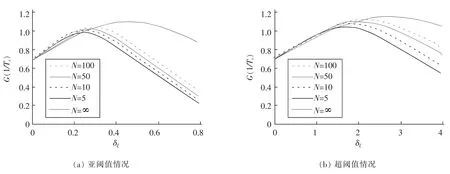
图4 阵列信噪比增益随阵列内部乘性噪声强度的变化曲线Fig.4 Changing curve of array SNR gain with the function of the amplitude of array noise

图4（a）和图4（b）分别绘出了信号幅值为A=0.34和A=0.5所对应的信噪比增益G（1/Ts）随内部乘性噪声强度σξ的变化曲线。为了对比阵列数目不同情况下的信噪比增益，图4给出了不同阵列数目的信噪比演化曲线。从图4可以看出当阵列数目N≥5时，信噪比增益G（1/Ts）开始表现为随内部乘性噪声强度σξ增加而单调增加达到一个峰值，而随着σξ强度的继续增加，信噪比增益呈现单调减小，这是一类典型的阵列随机共振现象。当阵列数目N→∞时，信噪比增益G（1/Ts）的局部最大值也随之增大，且对应于G（1/Ts）的最大值的内部乘性噪声区间向右偏移。此时，信噪比增益的最大值位置对应于乘性噪声强度σξ=1.4，这与图3中输出均值曲线一致。也就是说，噪声强度取σξ=1.4时的输出均值曲线振幅最大，信噪比增益也最大。当阵列数目N=∞，信噪比增益G（1/Ts）能达到全局最大值。值得指出的是，这里对应于阵列数目N=∞的信噪比增益G（1/Ts）数据是由任意两个处于独立的内部乘性噪声中的双稳态振子性能分析得到的。

图2、图3和图4曲线中表现的阵列随机共振及阵列信噪比增益大于1的物理机制，可以通过相互独立的阵列各子系统的内部乘性噪声ξ（t）来解释。一方面，阵列各子系统的内部乘性噪声诱导了阵列集体响应以达到其输出均值E［y（t）］，另一方面，阵列各子系统的内部乘性噪声也能对输入的加性噪声η（t）产生部分抑制作用从而减小输出的统计扰动。正如图3所描绘的结果一样，阵列各子系统的内部乘性噪声能减小稳态方差Cyy（0）和关联时间τ。

3 结论

本文研究了一类并联双稳振子组成的阵列信号处理中的随机共振现象及信噪比增益问题。阵列信号输入为包含加性噪声的正弦信号，当该输入信号通过并联双稳态振子组成的阵列时，受到相互独立的阵列各子系统内部乘性噪声的积极影响，使得该阵列系统中输出信噪比增益出现了典型的随机共振现象。有趣的是，这种由阵列各子系统内部乘性噪声诱导的非线性现象不仅适用于超阈值输入信号，也适用于亚阈值输入信号；因此这是一种新的随机共振现象，即阵列随机共振。

虽然，文献[8]在类似系统中也发现了信噪比增益大于1的现象。但是，该研究仅仅考虑了输入信号的噪声效应，其获得的信噪比增益大于1的结果是由外部输入的加性噪声所诱导的。而在实际情况下，输入信号在到达双稳并联阵列的传播路径中也应该考虑内部噪声效应。对于固定的加性噪声强度，本文证明了并联双稳态振子组成的阵列系统的输出信噪比增益是关于阵列大小的递增函数。当阵列数目增加到一定数目时，阵列的信噪比增益存在大于1的区域，且这一区域随着阵列数目的增加而扩展。本文的研究结果表明了阵列随机共振与文献[8]结果的不同之处。本文中的随机共振及信噪比增益是由每个双稳子系统中的乘性噪声诱导的双稳阵列的集振非线性反应。

此外，通过对并联双稳态振子组成的阵列非稳态输出均值和稳态自协方差函数的极限性质的研究，证明了无限并联双稳态振子组成的阵列信噪比增益问题可以简化为由任意两个相互独立处于不同内部乘性噪声驱动的双稳态振子的统计性能分析。这些研究结果不仅丰富了非线性阵列信号处理理论，也为复杂随机系统理论中噪声作用分析提供了一种新的思路[9-15]。

[1]BENZI R，SUTERA A，VULPIANI A.The mechanism of stochastic resonance[J].Journal of Physics A-Mathematica&General，1981，14：453-458.

[2]NICOLIS C，NICOLIS G.Stochastic aspects of climatic transitions-additive fluctuations Tellus[J].Tellus，1981，33：225-229.

[3]GAMMAITONI L，HANGGI P，JUNG P，et al.Stochastic resonance[J].Review of Modern Physics，1998，70：233-271.

[4]CHAPEAU BLONDEAU F，ROUSSEAU D.Enhancement by noise in parallel arrays of sensors with power-law characteristics[J]. Physical Review E，2004，70：060101（R）.

[5]CASADO PASCUAL J，GOMEZ ORDONEZ J，MORILLO M.Two-state theory of nonlinear stochastic resonance[J].Physical Review Letters，2003，91：210601.

[6]CHIZHEVSKY V N，GIACOMELLI G.Improvement of signal-to-noise ratio in a bistable optical system：comparison between vibrational and stochastic resonance[J].Physical Review A，2005，71：011801（R）.

[7]陈爱喜，陈渊，杨绍海.非对称半导体量子阱中的光学双稳态与多稳态[J].华东交通大学学报，2011，28（3）：65-68.

[8]CASADO J M，GOMEZ ORDONEZ J，MORILLO M.Stochastic resonance of collective variables in finite sets of interacting identical subsystems[J].Physical Review E，2006，73：011109.

[9]孙婧，段法兵.复杂随机系统的信噪比增益研究与阵列随机共振[J].复杂系统与复杂性科学，2006，3（2）：50-54.

[10]YAO C，ZHAN M.Signal transmission by vibrational resonance in one way coupled bistable systems[J].Physical Review E，2010，81：061129.

[11]LIU D，CHANG X，LIU Z，et al.Bistability and oscillations in gene regulation mediated by small noncoding RNAs[J].PLoS One，2011，6：e17029.

[12]WANG C，YI M，YANG K，et al.Noise-induced switches in network systems of the genetic toggle switch[J].BMC System Biology，2012，6：S9.

[13]张诚，冯亚萍.人工神经网络模型的江西省物流需求预测[J].华东交通大学学报，2014，31（4）：26-32.

[14]FENG T Q，YI M.Stochastic multiresonance induced by additive amplitude modulation signal and noise in a gene transcriptional regulatory model[J].Journal of Biological System，2015，23：289-302.

[15]ZENG C，YANG T，HAN Q，et al.Noises-induced toggle switch and stability in a gene regulation network[J].International Journal of Modern Physics B，2014，28：1450223.

Signal-Noise-Ratio Gain from Array of Complex System Induced by Multiplicative Array Noise

Feng Tianquan1，Yi Ming2
（1 School of Teacher Education，Nanjing Normal University，Nanjing 210023，China；2 College of Sciences，Huazhong Agricultural University，Wuhan 430070，China）

We investigated the array stochastic resonance induced by the multiplicative array noise in a parallel uncoupled array of identical bistable systems driven by the mixing signal of sinusoids and additive Gaussian white input noise.Our numerical simulating results showed that the signal-to-noise ratio gain could exceed unity for both subthreshold and suprathreshold sinusoids input when the array size reached a number.Interestingly，the region of SNR gain exceeding unity corresponding multiplicative noises could be extended as the array size arises.By simulating numerically the function limits of non-stationary array mean and stationary auto-convariance，we found that the performance of an infinite array can be approached by an array of two bistable oscillators operating in different noisy conditions.The present nonlinear phenomenon of SNR gain exceeding unity in parallel uncoupled arrays not only represent a promising application in array signal processing of complex random systems but also proved a new scheme for stochastic dynamics induced by the array noises.

array stochastic resonance；signal-noise-ratio（SNR）；bistable dynamic system；multiplicative array noise

O59；N93

A

1005-0523（2016）06-0103-07

（责任编辑 刘棉玲）

2016－09－26

国家自然科学基金项目（31100752，11275259，91330113）

冯天荃(1981—)，女，讲师，博士，研究方向为统计物理和生物物理。