基于混合和声搜索算法求解旅行商问题

曾 毅，朱旭生

（华东交通大学理学院，江西 南昌330013）

基于混合和声搜索算法求解旅行商问题

曾 毅，朱旭生

（华东交通大学理学院，江西 南昌330013）

针对旅行商问题，提出了一种新的混合和声搜索算法。混合算法利用和声算法和蚁群算法机理，重新定义和声算法的即兴创作操作，解决新生成的和声不能很好地保持和声记忆库中和声的优良基因片段的问题。为维持混合算法的多样性，给出新的记忆库更新策略。对旅行商问题进行测试，仿真结果表明混合算法的有效性。

旅行商问题；和声搜索算法；蚁群算法

旅行商问题[1]（traveling salesman problem，TSP）可描述为：给定单个城市和两两城市之间的距离，求一条经过各城市一次且仅一次后在回到原出发城市的最短路线。该问题不仅具有广泛的应用背景和重要理论价值，而且是一典型的组合优化NP难问题,常常用来验证某一算法的有效性。

求解旅行商问题的算法可分为精确算法和启发式算法。精确算法能找到问题的最优解，但随着问题的规模增大，其运行时间按指数增加，所以仅适合求解小规模问题。而启发式算法由于其独特的运行机制能在合理的时间内得到问题的满意解，因而设计有效的启发式算法是求解旅行商问题一个重要的研究方向[2]。

和声搜索算法（harmony search algorithm,HS）[3]是Geem Z W等人受音乐家即兴创作过程的启发而提出的一种元启发式全局搜索算法。算法将乐器对应于优化问题的各个变量，乐器的音调对应于变量的取值，创作的和声对应于解向量，和声评价结果对应于目标函数，和声记忆库对应于种群，而音乐的创作过程即为种群的进化过程。和声搜索算法原理简单，参数较少，且易于实现。最近几年和声搜索算法成功地应用于公交路线设计问题[4]、水网调度问题[5]、竞争选址问题[6]、车辆路径问题[7]及旅行商问题[8]等组合优化问题，本文针对旅行商问题，提出了一种新的混合和声搜索算法。混合算法利用和声算法和蚁群算法的机理，重新定义了和声算法的即兴创作操作，解决了新生成的和声不能很好地保持和声记忆库中和声的优良基因片段问题。为维持算法的多样性，给出了新的记忆库更新策略。对旅行商问题进行测试，仿真结果表明混合算法的有效性。

1 和声搜索算法

设所求的离散型变量非约束最优化问题为

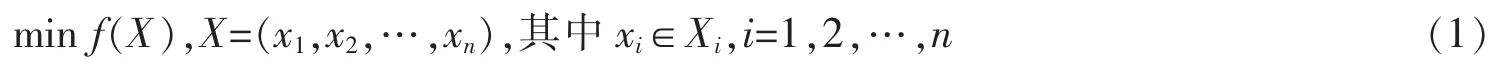
式中：f（X）为目标函数；X为决策变量xi构成的解向量；Xi={xi（1），xi（2），…，xi（ki）}为决策变量xi的取值空间,其中ki是决策变量xi可能的取值个数。

基本和声搜索算法的步骤如下[9]：

步骤1 初始化算法参数。和声搜索算法主要参数：和声记忆库大小（harmony memory size，HMS），和声记忆库的思考概率（harmony memory considering rate，HMCR），音调微调概率（pitch adjusting rate,PAR），创作次数（NI）等。

步骤2 初始化和声记忆库。随机生成HMS个和声：X1，X2，…，XHMS，将和声及相应的目标函数值放入和声记忆库（harmony memory，HM）。设最优化问题决策变量个数为n，其和声记忆库HM可用如下矩阵表示：

步骤3 创作新和声。在这一步骤中，和声搜索算法即兴产生一个新的和声。新和声的产生基于3种操作：①记忆思考；②音调微调；③随机选择音调。具体操作如下：

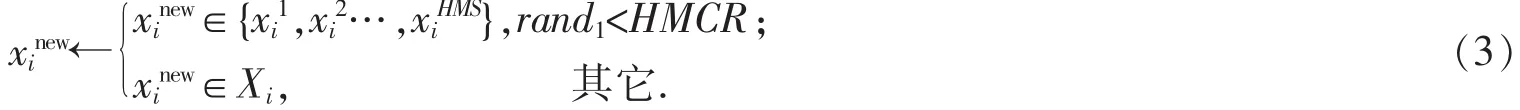
式中：rand1表示［0，1］上均匀分布的随机数。

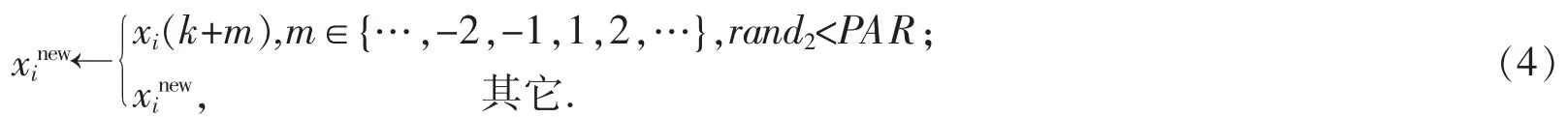
式中：rand2表示［0，1］上均匀分布的随机数；微调之后的取值；xi（k）为微调之前的取值，此时xi（k+m）表示在xi（k）的“左右邻居”中重新选择。

步骤4 更新和声记忆库。若新和声Xnew好于声记忆库中的最差的和声Xworst，即f（Xnew）＜f（Xworst）=max{f（Xj）｜j=1，2，…，HMS}，那么用新和声替代和声记忆库中的最差和声。

步骤5 检查是否达到算法终止条件。如果创作（迭代）次数小于设定的创作（迭代）次数NI，则返回步骤3；否则，停机输出结果。

2 混合和声搜索算法

2.1 编码

旅行商问题采用自然数编码，即利用城市在路线中的位置来表示一条路线。这种编码方式自然、简单，且适用于不同规模的旅行商问题。若9城市的旅行商问题的路线为(5-1-7-8-9-4-6-2-3-5)，则相应的编码为(5 1 7 8 9 4 6 2 3)。

2.2 创作新和声的改进

和声搜索算法最初主要是针对连续变量的优化问题求解。但要使算法成功地求解旅行商问题，关键是要保证迭代过程生成的新和声满足2个条件：①新和声能很好地继承和声记忆库中和声的优良基因片段；②新和声是一个可行解。而按和声搜索算法步骤3生成的新和声很可能是一个不可行解，即生成的和声编码中出现重复的基因码。为此，文献[8]提出分散学习策略和分块学习策略，将不可行解修复为可行解，但在修复的过程中，记忆库中和声的优良基因片段不能很好地被继承下来。考虑到和声搜索算法的新和声的生成过程实质上是一个继承和探索的过程，即新和声从和声记忆库（HM）中以概率HMCR·（1-PAR）所得到的分量就是一个继承过程，而微调和随机产生的分量就是一个探索过程。为此，我们设计了新和声的生成算法，使生成的新和声满足上述的2个条件。

新和声的生成算法如下：

Step1 置s=1。从旅行商问题中的n个城市中随机选择一个城市作为第一个旅行的城市。设城市c1为选择的第一个城市，current_city为当前旅行的城市，置current_city=c1。集合unvisited_city={1，2，…，n}-{c1}为未旅行的城市的集合。

Step2 随机生成1～HMS之间的整数k，设HM中第k个和声中的current_city之后的城市为j。按式(5)确定下一个旅行的城市next_city。

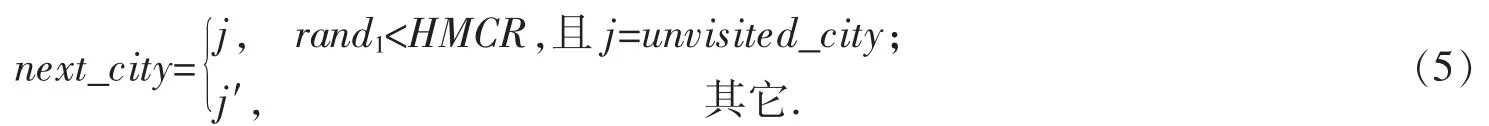
式中，rand1为 ［0，1］上均匀分布的随机数。城市j′依转移概率按轮盘赌法确定，即先计算当前城市current_city到unvisited_city中各城市的转移概率，然后采用轮盘赌法确定下一个访问城市j′。设和声搜索算法的第t次迭代从城市i转移到城市j概率为Pij（t），Pij（t）的值可按式（6）计算。待next_city确定后，置current_city=next_city，unvisited_city=unvisited_city-{next_city}。

式中：τij（t）为城市i与城市j连接路径上的信息素浓度；ηij（t）=1/d（i，j）为启发函数，表示从城市i转移到城市j的期望程度；α为信息素重要程度因子，其值越大，表示信息素的浓度在转移中起的作用越大；β为启发函数重要程度因子，其值越大，表示启发函数在转移中的作用越大。

Step3 置s=s+1，若s≤n，转Step2；否则，将每次取到的当前城市依次排列,得到准新和声。

Step4 准新和声的微调及信息素浓度的更新。考虑到标准的音调微调操作不利于旅行商问题的邻域解的搜索。为此，设计基于进化逆转操作的和声微调操作，即准新和声生成后，若随机数rand1＜PAR，对准新的和声连续实施M次进化逆转操作。进化逆转操作是遗传算法求解旅行商问题常用的一个操作。这里的“进化”是指逆转操作的单方向性，即经进化逆转操作后，得到路径更短的和声，则用此和声替换准和声，并在此基础上进行下一轮的进化逆转操作（注：此时的进化逆转操作的次数小于M）。若实施M次进化逆转操作后没有得到路径更短的和声，则认为M次进化逆转操作无效，准新和声不变。仍以9个城市的旅行商问题为例，说明进化逆转操作的过程：

产生2个1～9之间的随机整数r1，r2，且r1＜r2，不妨设r1=2，r2=7，若逆转操作前的和声为（1|2 6 4 9 8|7 3 5），则逆转操作后的和声为（1|8 9 4 6 2|7 3 5）。

准和声经逆转操作后的和声称之为新和声。当新和声好于和声记忆库中的最差和声时，各个城市间连接路径上的信息素浓度按（7）式进行实时更新；否则，各个城市间的连接路径上的信息素浓度不变。

式中：参数ρ（0＜ρ＜1）表示信息素的挥发因子；△τij表示在城市i与城市j连接路径上新增加的信息素浓度，△τij按（8）式计算。

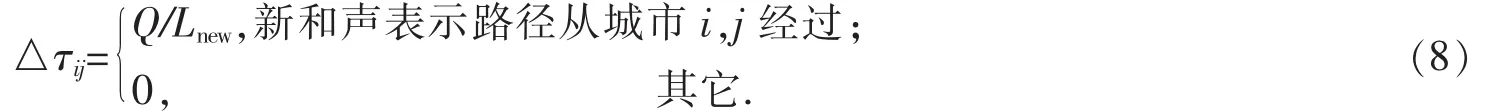
式中：Q为信息素强度；Lnew为新和声对应的路径长度。

2.3 和声记忆库的更新策略的改进

在标准和声搜索算法中，如果新产生的和声优于和声记忆库中的最差和声，则将新和声替代和声记忆库中最差的和声。这种更新策略随迭代的进行必然会降低和声搜索算法的多样性，导致早熟收敛。考虑到和声记忆库的规模一般不大，新的更新策略为：将新产生的和声与和声记忆库的和声逐一比较。当且仅当和声与记忆库中的和声均不相同，并且好于和声记忆库中的最差和声，则将新和声替换记忆库中的最差和声。

3 仿真分析

选文献[10-11]中的旅行商问题作为测试问题。这2个旅行商问题分别称为14-TSP和30-TSP。另外，选遗传算法（GA）、模拟退火算法（SA）及蚁群算法（ACO）3种算法和本文提出的混合和声搜索算法（HS-ACO）作对比测试。GA，SA及ACO算法的参数取值与文献[11]相同，其中GA算法的参数：种群规模Popsize=100，选择概率Ps=0.9，交叉概率Pc=0.9，变异概率Pm=0.05；SA算法的参数：初始温度T0=1 000，结束温度Tend=1e-3，降温速度q=0.966，链长L=200；ACO算法的参数：蚂蚁数量取旅行商问题的城市数，信息素重要程度因子α=1，启发函数重要程度因子β=5，信息素挥发因子ρ=0.1，信息素释放总量Q=20，在初始时刻t=0，各路径上信息量τij（0）=1。HS-ACO算法的参数：和声记忆库的规模HMS=10，最大迭代次数NI=400,和声记忆库取值概率HMCR依迭代次数线性递增从HMCRstart变到HMCRend，即

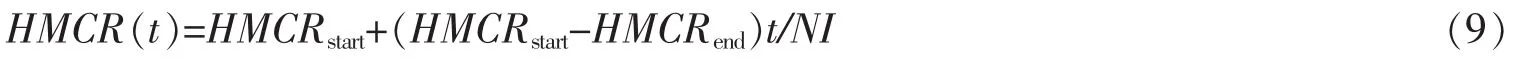
本文HMCRstart=0.60，HMCRend=0.95，和声音调微调概率PAR=0.3，逆转操作次数M=20，其余参量的取值与蚁群算法相同。对选取的2个旅行商问题每种算法重复运行20次，测试结果如表1和表2所示，表中MEAN，BEST，WORST，SD和SR分别表示算法连续运行20次得到的最优解的平均值、最好值、最差值、均方差及达到最优值的比例。图1为收敛曲线，图中横坐标为迭代次数，纵坐标为最短路径平均长度。

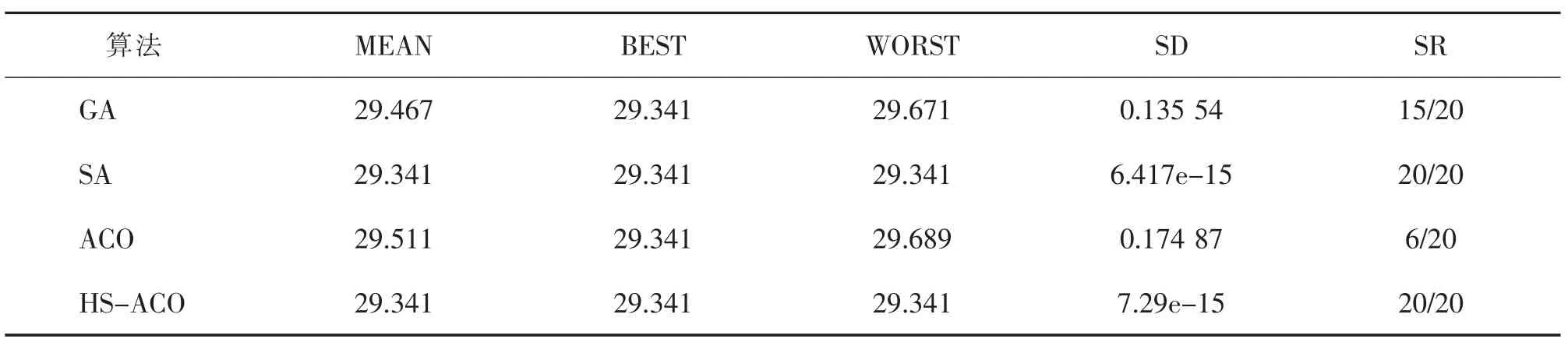
表1 4种算法对14-TSP的仿真实验结果Tab.1 Simulation results of four kinds of algorithms for 14-TSP

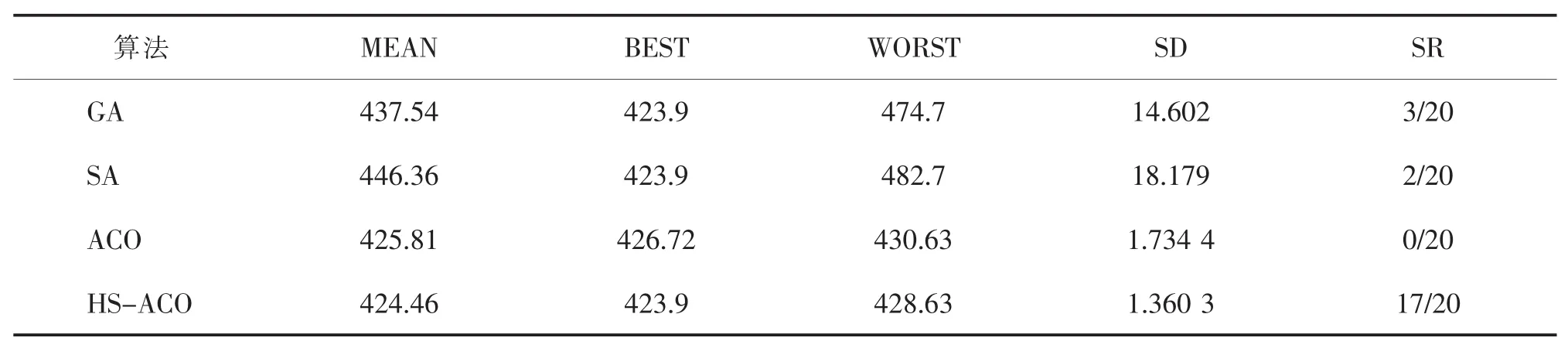
表2 4种算法对30-TSP的仿真实验结果Tab.2 Simulation results of four kinds of algorithms for 30-TSP

从测试问题的计算结果来看，HS-ACO算法的评价指标，即算法最优值、平均值、最差值、均方差及达到最优值的比例都好于算法GA，SA，ACO的评价指标。随着旅行商问题的城市数增加，GA，SA算法的各项评价指标明显变差。虽然ACO算法能找到较优的解，均方差也较小，但由于算法具有较强的鲁棒性，明显地出现停滞现象，收敛到局部最优解，30-TSP达到最优值比例为0/20。而HS-ACO算法的各项评价指标依然很好，与其它算法相比仍然保持了明显的优势，30-TSP达到最优值比例17/20,远远高出其它算法。

从图1测试问题的收敛曲线来看，当旅行商问题的城市数由14个增加到30个时，HS-ACO算法收敛速度和解的质量明显地好于GA，SA，ACO算法。这表明随旅行商问题城市数的增加，单一机制的优化算法很难实现全局优化，效率较低，而混合和声搜索算法将多种优化机制相结合，取长补短，能较好地保持算法的全局优化性能。

图1 测试问题收敛曲线Fig.1 Convergence curves of test questions

4 结语

针对旅行商问题，提出一种新的混合和声搜索算法（HS-ACO）。该算法有以下几个特点：

1）即兴创作的选择操作与传统的基于分量的选择操作不同，利用了旅行商问题中节点与节点的强关联性，能较好地继承记忆库和声的优良基因片段。测试结果表明该选择操作可行性，对其它启发性算法在求解旅行商问题有一定的借鉴作用。

2）微调操作在准新和声生成之后，这与和声搜索算法微调操作在新和声生成的过程中进行不同，避免了微调操作的“随机性”，能保证新的和声“好上加好”。

3）采用了新的记忆库更新策略，保证了算法多样性，使算法更容易跳出局部最优解搜索到全局最优解。

接下来的工作是将本文提出的算法运用到其它的组合优化问题，进一步验证算法的性能。

[1]胡能发，康立山，陈毓屏.构建“基因库”求解TSP问题的混合遗传算法[J].计算机工程与应用，2003，39（11）：75－76.

[2]田贵超，黎明，韦雪洁.旅行商问题(TSP)的几种求解方法[J].计算机仿真，2006，23（8）：153-157.

[3]GEEM Z，KIM J，LOGANATHAN G.A new heuristic optimization algorithm:harmony search[J].Simulation，2001，76（2）：60－68.

[4]GEEM Z W，LEE K S，PARK Y.Application of harmony search to vehicle routing[J].American Journal of Applied Sciences，2005，2（12）：1552－1557.

[5]GEEM Z W.Optimal scheduling of multiple dam system using harmony search algorithm[C]//Computerional and ambient intelligence，Berlin：Springer，2007：316-323.

[6]于宏涛，高立群，吕勇军.基于混合和声搜索算法求解竞争选址问题[J].控制与决策，2013，28（7）：1083-1093.

[7]王英博，王琳，李扬，等.改进的遗传和声算法及其在车辆路径中的应用[J].计算机测量与控制，2011，19（12）：3068-3071.

[8]李俊青，王玉亭，潘全科，等.混合离散和声搜索算法求解旅行商问题[J].微电子学与计算机，2009，26（3）：17-21.

[9]赵玉新，YANG XINSHE，刘利强.新兴元启发式优化方法[M].北京：科学出版社，2013：203-204.

[10]敖友云，迟洪钦.基于遗传算法求解TSP问题的一种算法[J].计算机数字与工程，2006，34（4）：52-55.

[11]史峰，王辉，郁磊，等.MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011：183-185.

Hybrid Harmony Search Algorithm for Traveling Salesman Problem

Zeng Yi，Zhu Xusheng
（School of Science，East China Jiaotong University，Nanchang 330013,China）

Aiming at traveling salesman problem,this paper puts forward a new hybrid harmony search algorithm. By using the mechanism of harmony search algorithm and ant colony algorithm,improvisation operator of hybrid algorithm is redefined so as to solve the problem that the newly-generated harmony doesn’t well maintain the excellent gene segment in harmony memory.In order to maintain the diversity of hybrid algorithm,a new memory updating strategy is given.Finally,the algorithm is applied and tested in traveling salesman problem.The results of simulation indicate the effectiveness of the proposed algorithm.

traveling salesman problem；harmony search algorithm；ant colony optimization

TP301.6

A

1005-0523（2016）06-0131-06

（责任编辑 刘棉玲）

2016－04－10

国家自然科学基金项目（11161021）；华东交通大学科研项目（09111114）

曾毅（1965—），男，副教授，研究方向为智能计算。