电磁开关强非线性系统主共振分析

杨志安，赵利沙

（1.唐山学院 唐山市结构与振动工程重点实验室，河北 唐山 063000；2.华北理工大学 机械工程学院，河北 唐山063000）

电磁开关强非线性系统主共振分析

杨志安1，赵利沙2

（1.唐山学院 唐山市结构与振动工程重点实验室，河北 唐山 063000；2.华北理工大学 机械工程学院，河北 唐山063000）

以电磁开关系统为研究对象，根据拉格朗日麦克斯韦方程建立三阶非线性动力学模型，应用MLP法得到电磁开关强非线性系统主共振的幅频响应方程及位移和电流分别随时间变化的振动规律，分析系统各参数对系统主共振幅频响应曲线的影响。结果表明，系统的幅频响应曲线存在跳跃现象；随着阻尼系数的增大，系统的振幅减小；随着激励电压幅值增大，系统的振幅和共振区域增大；随着电阻增大，系统的振幅和共振区域减小。

振动与波；电磁开关；拉格朗日麦克斯韦方程；MLP法；主共振；强非线性

近年来，随着现代汽车对起动机提出了体积小、重量轻、性能可靠、功率大、寿命长的要求，汽车起动机电磁开关的设计与制造不断向前发展[1]。起动机是启动系统的重要组成部分，由电磁式控制装置、传动机构和直流电动机构成[2]。电磁式控制装置是一种电磁式控制开关，即电磁开关[3]。电磁开关是汽车起动机中的一种重要的控制元件，也是最容易出现故障的元件，它的主要作用就是使驱动齿轮与飞轮能够快速啮合和退出，并将起动机的电枢主电路与蓄电池接通，使起动机电枢在磁场中旋转，进而起动发动机[4]。电磁开关性能的好坏直接关系到起动机能否正常工作，因此对电磁开关的研究具有十分重要的意义，应予以足够的重视。电磁开关在工程中有广泛的应用，在机动车及内燃机起动机中都可以看到电磁开关的存在。电磁开关可以抽象为RLC电路与弹簧耦合系统，是典型的机电耦合系统。以往学者们已经提供一些相关经验可供参考。文献［5-6］研究了RLC电路弹簧耦合系统的非线性振动，得到了受简谐激励的Mathieu方程的级数形式解，并用数值解法验证级数形式解的正确性。文献[7-8]以RLC串联电路与微梁耦合系统为例，应用Lagrange-Maxwell方程建立静电驱动微梁的耦合数学模型。分析了吸合电压和电震荡两种动力学问题。继而又研究了RLC串联电路与微梁耦合系统1∶2型内共振问题。

上述关于RLC电路耦合系统研究多数是基于弱非线性。目前未见对电磁开关系统建立动力学模型的文献，关于RLC电路耦合系统强非线性系统主振动的研究也不多。针对简谐激励作用下的电磁开关强非线性[9]系统进行研究。应用Lagrange-Maxwell方程建立动力学模型，运用MLP法对系统的非线性振动方程[10-11]进行分析，得到系统的幅频响应方程及位移和电流分别随时间变化的振动规律，并分析系统各参数对振幅和共振区域的影响。

1 电磁开关系统强非线性动力学方程

图1是DK114型汽车起动机电磁开关工作原理设计图。从图中可以看出，电磁开关的基本组成部分包括触片回复弹簧、开关触片、触片压簧、静铁芯、维持线圈、吸引线圈、动铁芯、顶齿弹簧、阀芯回复弹簧等[12]。线圈通电后产生电磁吸力，使活动铁芯移动，接通励磁绕组电路，产生励磁，电枢工作，从而带动发动机起动。断电后，活动铁芯在弹簧力下复位，等待下次启动[3]。

图1 电磁开关结构示意图

汽车起动机电磁开关的简化模型如图2所示，电源的电动势为U(t)，电阻为r，电路电流为i，线圈的自感为L(x)，电源、电阻及电感组成回路。电磁铁的质量为m，弹簧刚度为k，电磁铁线圈的自感为Lm(x)，x为自弹簧平衡位置算起的水平位移，电磁铁上线圈激励电压为Um，电磁铁上线圈电阻为R，电磁铁上线圈电流为im，M(x)为电路与电磁铁的互感，rv为线圈与磁铁之间的摩擦阻力系数。

图2 电磁开关结构简图

选位移x、电路电流i、电磁铁上线圈电流为im广义坐标。

拉格朗日函数L=T+Wm-V为

根据拉格朗日麦克斯韦方程[13]，可以建立其非线性动力学方程

电磁开关的数学模型表达式（5）是以位移为广义坐标的2阶振动微分方程和以电流为广义坐标的1阶振动微分方程组成的非线性振动方程组。式（5）是典型的机电耦合系统。

2 运用MLP方法分析电磁开关强非线性系统主共振[14-15]

所谓主共振是指外激励频率Ω接近派生系统固有频率ω0时的共振。根据式（5）中ω02x项与η2x3项系数进行比较可知η2相对较大，是强非线性问题。将式（5）的第二式代入第一式，并引入非小参量ε

式中a为系统稳态解振幅，ω1为调谐值。

在电磁开关强非线性系统的主共振研究中，将式（5）的第二式代入第一式，对x采用摄动法展开，进行求解，得出系统的幅频响应方程，但是得不到系统中位移和电流随时间变化的振动规律。因此，需要进一步对电磁开关强非线性系统主共振的时间历程进行分析。

选择DK114型汽车起动机电磁开关参数：r=12 Ω，k=18 N/m，k1=8×105N/m，rv=0.01 kg ·s/m3，m=2 kg，U0=12 V ，L=0.1 H ，M0=0.15 H ，

图3至图7为电磁开关系统表达式（5）主共振的幅频响应曲线。

图3 不同阻尼值情况下的幅频响应曲线

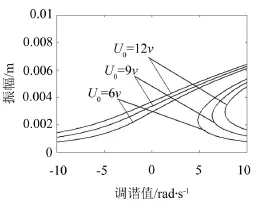
图4 不同电压值情况下的幅频响应曲线

图5 不同电压值情况下的幅频响应曲线

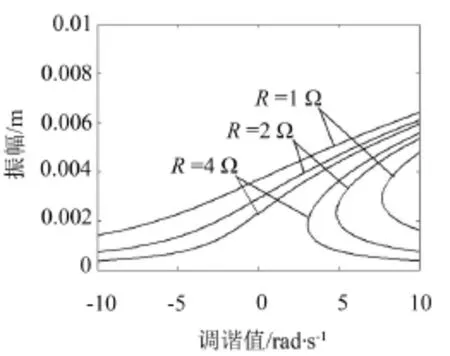
图7 不同电阻值情况下的幅频响应曲线

图3为电磁开关系统主共振随阻尼系数rv变化的幅频响应曲线，由图3可知，当调谐值由低向高或由高向低连续变化时,位移的振幅会出现“跳跃”现象。当增大线圈与磁铁之间的摩擦阻力系数时，系统受到的阻力增大，振幅减小，对共振区域的影响不明显。

图4是电磁开关系统主共振随激励电压幅值U0变化的幅频响应曲线。由图4可知，激励电压幅值U0的改变对系统振幅影响比较大，随着激励电压幅值U0的增大，“跳跃”现象越明显，振幅和共振区域增大，由式（15）可知振幅与激励电压幅值U0是正比关系。

图5是电磁开关系统主共振随电磁铁上线圈电压Um变化的幅频响应曲线。由图5可知，随着电磁铁上线圈激励电压Um的增大，“跳跃”现象越明显，振幅和共振区域增大。

图6是电磁开关系统主共振随电阻r变化的幅频响应曲线。由图6可知，随着电阻r的增大，“跳跃”现象越不明显，振幅和共振区域减小。

图7是电磁开关系统主共振随电磁铁上线圈电阻R变化的幅频响应曲线。由图7可知，随着电磁铁上线圈电阻R的增大，“跳跃”现象越不明显，振幅和共振区域减小。

3 电磁开关强非线性系统主共振时间历程

由电磁开关的数学模型表达式（5）引入非小量参数ε，整理为

对系统进行变换，同时考虑共振响应频率和相位的变化，令H=η6cosθ，K=η6sinθ，则系统重新写为

对x、i采用摄动法展开

将式（9）、式（10）、式（11）、式（12）、式（18）代入式（17），同时比较方程两边α的幂次得

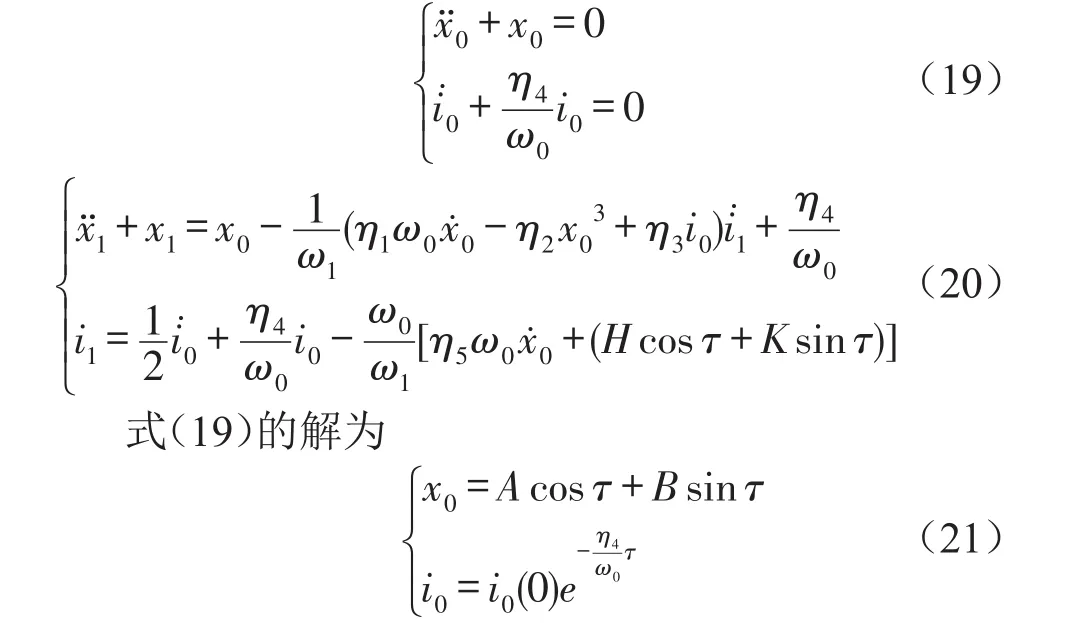
考虑式（19）第一个式子的边界条件可设：x(0)=p，(0)=0

则式（21）转化为

由初始条件可知

可得微分方程的一次近似解为

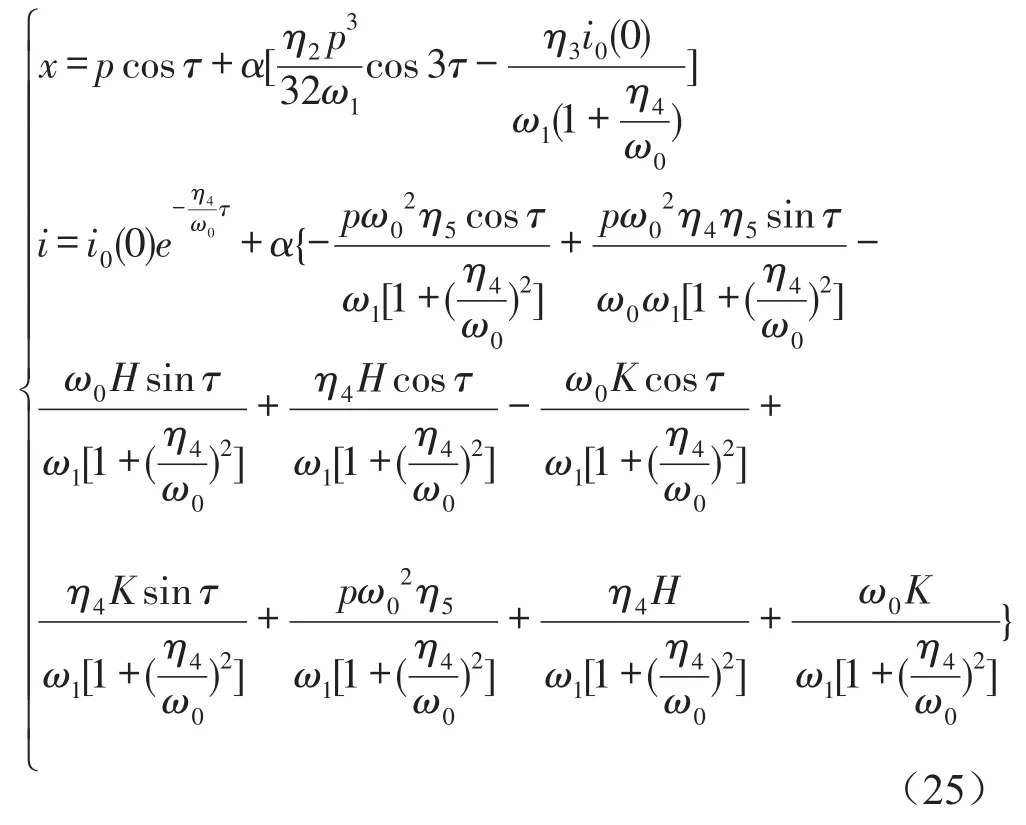
在对电磁开关强非线性系统主共振的时间历程进行分析时，同时对x、i采用摄动法展开，进行求解，得到了系统中位移和电流分别随时间变化的振动规律。

将振幅设定在约束范围之内时，选取ω1=0.1 rad/s，p=α(0)=0.004 m，电流初始值为i(0)=0.05 A。由式（25）可得系统解析解的时间响应曲线。

图8为电磁开关系统位移时间响应曲线。由图8可知，系统的一次近似解与零次近似解曲线相比，一次近似解的精度较高，振幅稍变大，一次近似解存在多频成分。

图8 时间响应曲线

图9、图10为电磁开关系统电流时间响应曲线。由图9可知，随着时间的增大，电流越来越小，直到衰减为零。

图9 时间响应曲线

由图10可知，随着时间的增大，电流迅速衰减为零，时间继续增大，电流开始做简谐振动。

图10 时间响应曲线

4 结语

根据拉格朗日麦克斯韦方程建立电磁开关系统动力学模型，由线性项系数和非线性项系数对比可知为强非线性系统。应用MLP法研究电磁开关强非线性系统主共振问题，得到系统的幅频响应方程及其位移和电流分别随时间变化的振动规律，并分析了系统振幅和共振区域随各参数的变化。结果表明增大磁铁的摩擦阻力系数可以减小振幅，对共振区域的影响不明显；增大激励电压幅值和电磁铁上线圈电压可以使振幅和共振区域增大；增大电阻和电磁铁上线圈电阻能够减小共振的振幅和共振区域。

[1]夏利波.汽车起动机电磁开关的设计研究[D].杭州：浙江大学，2011.

[2]查小净，李骏，吴东盛.起动机直接温控的过热保护电路设计[J].制造业自动化，2011，33(5)：129-131.

[3]于成伟，马秀艳.起动机用电磁开关[J].汽车电器，2009，2：29-33.

[4]张胜川，边建华.汽车起动机电磁开关触片触点烧蚀原因探析[J].汽车电器，2010，4：28-32.

[5]崔一辉，杨志安.RLC电路弹簧耦合系统的级数解[J].振动与冲击，2006，25(4)：76-77.

[6]催一辉，杨志安.RLC电路弹簧耦合系统的非线性动力学分析[J].河北理工大学学报，2005，27(4)：49-54.

[7]杨志安，贾尚帅.RLC串联电路与微梁耦合系统的吸合压电与电震荡[J].应用力学学报，2010，27(4)：721-726.

[8]杨志安，贾尚帅.RLC串联电路与微梁耦合系统1:2内共振分析[J].应用力学学报，2010，27(1)：80-85.

[9]TANG J S,QIAN C Z.The asymptotic solution of the nonlinear Klein-Gordon equation[J].Journal of Sound and Vibration,2003,268(5):1036-1040.

[10]程欧，苟向锋.多自由度齿轮系统非线性动力学分析[J].噪声与振动控制，2015，35(6)：30-35.

[11]关卓怀，蔡敢为.转子弯扭耦合振动共振特征分析[J].噪声与振动控制，2016，36(1)：5-10.

[12]罗石，孙雷.汽车起动机电磁开关动态行程分析[J].淮海工学院学报，2016，25(1)：11-15.

[13]YANG ZHIAN,LI WENLAN,QIU JIAJUN.Lagrange-Maxwellequationsand parameterresonanceofthe generator under magnetic saturation[J].Applied Mathematics and Mechanics,2007,28(11):1379-1386.

[14]钱长照.强非线性Duffing系统分岔响应分析的MLP方法[J].动力学与控制学报，2008，6(2)：126-129.

[15]CHEUNG Y K,CHEN S H,LAU S LA.Modified lindstedt Poincare method for certain strongly nonlinear oscillators[J].International Journal of Non-Linear Mechanics,1991,26(3):367-378.

Analysis of Primary Resonance of Strong Nonlinear Solenoid Switch Systems

YANG Zhi-an1,ZHAO Li-sha2
(1.Key Laboratory of Structure and Vibration Engineering of Tangshan,Tangshan College, Tangshan 063000,Hebei China; 2.College of Mechanical Engineering,North China University of Technology, Tangshan 063000,Hebei China)

A solenoid switch system is studied.Its nonlinear dynamic model of order three is established based on Lagrange-Maxwell equation.The amplitude frequency response equation and the vibration laws of displacement and current changes with time of the strong nonlinear system are obtained by means of the MLP method.The influence of the parameters of the solenoid switch system on the primary resonance response curves is analyzed.Results indicate that the amplitude of the primary resonance of the system reduces with the increasing of the damping coefficient.The amplitude and resonance region of the primary resonance of the system increase with the increasing of the excitation voltage amplitude and decrease with the increasing of the resistance.

vibration and wave;solenoid switch;Lagrange-Maxwell equation;MLP method;primary resonance; strong nonlinearity

O322

：A

：10.3969/j.issn.1006-1335.2016.06.005

1006-1355(2016)06-0021-05+44

2016-04-05

河北省自然科学基金项目（A200900097）

杨志安（1963-），男，河北省秦皇岛市人，博士，教授，硕士生导师，研究方向为机构学与机械动力学。E-mail:yangzhi_an@163.com

赵利沙（1988-）女，河北省邯郸市人，硕士研究生，研究方向为机构学与机械动力学。E-mail:948281620@qq.com