基于多层次蒙特卡罗方法的巴黎期权定价
宋 斌,林则夫,张冰洁
(1.中央财经大学管理科学与工程学院 北京 100081;2.北京航空航天大学管理学院 北京 100191)
基于多层次蒙特卡罗方法的巴黎期权定价
宋 斌1,林则夫1,张冰洁2
(1.中央财经大学管理科学与工程学院 北京 100081;2.北京航空航天大学管理学院 北京 100191)
巴黎期权是由障碍期权发展起来的一种复杂的路径依赖期权,其允许期权持有者在标的资产价格满足在某个给定的价格水平(障碍价格)之上或者之下连续或累计停留预先设定的一段时间的条件下,以预先约定的价格(执行价格)买入或卖出某种标的资产。目前巴黎期权定价的主流数值方法有二叉树方法、有限差分法和蒙特卡罗方法。论文的研究结果表明,在给定的精度条件下,与标准蒙特卡罗方法相比,多层蒙特卡罗方法能够将运算成本从O(ε-3)减少到O(ε-2(logε)2);反之,在给定的计算成本条件下,相对于标准蒙特卡罗方法,多层蒙特卡罗方法能够更快地收敛到真值附近。本文将其应用于巴黎期权的定价计算中,增加了巴黎期权的数值算法选择范围,并提高了巴黎期权定价的精度。
巴黎期权;标准蒙特卡罗算法;多层蒙特卡罗算法;计算成本
1 引言
巴黎期权是一种复杂的路径依赖期权,根据持续时间类型,可以分为累计巴黎期权(Cumulative Parisian Option)和连续巴黎期权(Consecutive Parisian Option)和移动窗口巴黎期权(Moving Window Parisian Option)。目前巴黎期权的主要的研究方法有概率方法、偏微分方程(以下简称PDE)方法以及数值方法。概率方法最先是由Chesney、Jeanblanc和Yor[1]提出,该文得出了巴黎期权价格的拉普拉斯变换形式,但并没有给出相应的逆拉普拉斯数值解Haber、Schonbucher和Wilmott[2]从PDE的角度给出了连续巴黎期权和累计巴黎期权的三维PDE,由于无法得到解析解,文章用显性有限差分的方法对该PDE进行了数值计算。同样,Vetzal和Forsyth[3]也使用了有限差分法对PDE进行求解,得出了相应结果并将该算法用在转换期权(Switch Options)和阶梯期权(Step Options)上。宋斌、周湛满、魏琳和张冰洁[4]重新研究了巴黎期权PDE的边界条件,运用方向导数写出了新的PDE,并运用有限差分方法进行数值计算。Avellaneda和 Wu Lixin[5]提出了计算巴黎期权定价的三叉树方法。Costabile[6]采用二叉树(CRR)方法计算了具有常数障碍水平以及指数障碍水平的巴黎期权的价格。Anderluh[7]在连续时间框架下通过停时模拟的方法来计算累计巴黎期权和连续巴黎期权的价格。郭冬梅、宋斌和汪寿阳[8]给出了巴黎期权的倒向随机微分方程表达式,并将其转化为巴黎期权非线性定价的偏微分方程,并在金融市场收益率不确定的情形以及存贷利率不同的情形下进行定价和具体的数值分析。巴黎期权还可以应用于投资决策领域。谭英双、衡爱民和龙勇[9]在不对称双头垄断期权博弈模型基础上讨论了利润流现值和沉没投资成本为梯形模糊数的情形并进行了扩展,构建了模糊环境下追随者领导者的投资价值和投资临界值的模糊表达式并进行数值分析。

与其他数值方法相比,蒙特卡罗方法一是具有算法灵活、易于实现和改进的优势;二是模拟估计误差及收敛速度与所要解决问题的维数有较强的独立性,因而能够较好地解决复杂衍生证券的高维定价问题。例如在连续时间框架下,移动窗口巴黎期权的PDE将是一个无限维PDE,而蒙特卡罗方法可以较好地解决高维定价问题。当运用蒙特卡罗方法计算路径依赖期权等较为复杂的衍生工具时,会产生较大的估计方差,而传统的方差减少技术也无法达到理想的效果。研究结果表明,在给定精度条件下,与标准蒙特卡罗方法相比,多层蒙特卡罗方法能够有效降低运算成本,因此更适合应用于巴黎期权的定价。巴黎期权提高了交易者操纵股价的成本,保护了交易对手的利益,较好地克服了障碍期权的局限性。
本文首次将多层蒙特卡罗算法用于巴黎期权,一方面在理论上拓宽了多层蒙特卡罗方法的应用领域。另一方面不仅提高了巴黎期权定价的精度,而且扩展了巴黎期权的数值方法选择范围,为巴黎期权的广泛应用奠定了较好的数值方法基础。
2 多层蒙特卡罗方法
2.1 基本原理
假设标的资产价格满足式(2.1)所示的几何布朗运动:
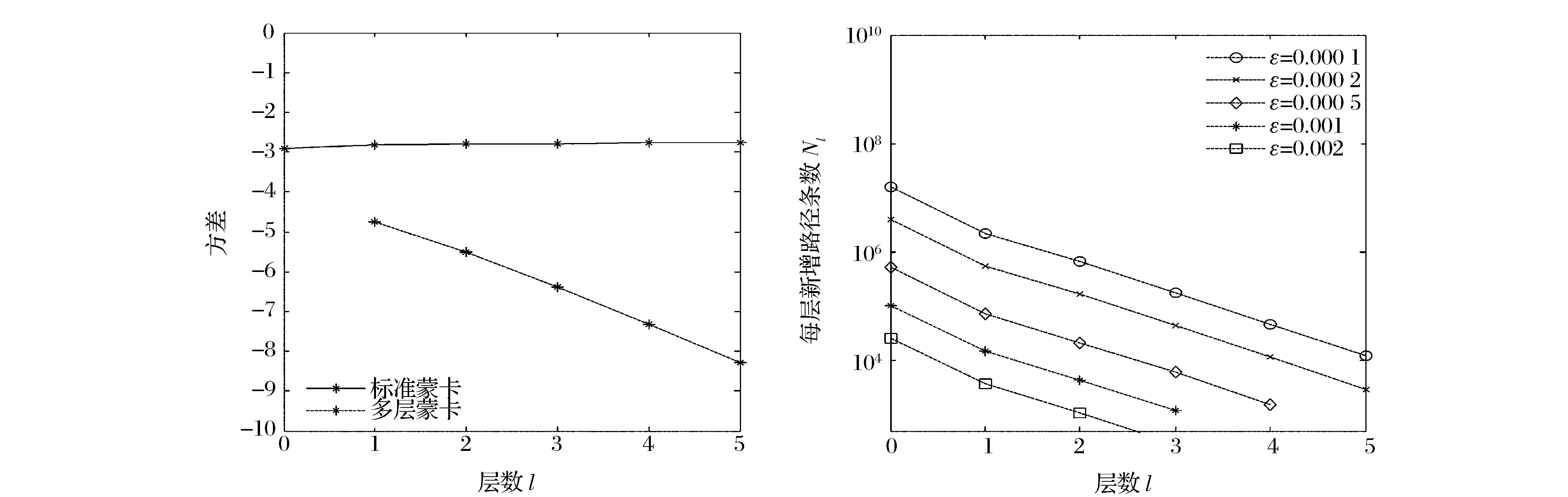
dS(t)=aS(t)dt+bS(t)dW(t),0 (2.1) 由风险中性定价原理可知,对于给定的S0,要计算的期权价格是f(S(T))的期望值。其中,f(S)作为终端支付函数具有一致的Lipschitz边界。即存在常数c,使得对于任意U,V有|f(U)-f(V)|≤c||U-V||。式(2.1)的一个简单的以h为时间间隔的欧拉离散表达形式是: (2.2) (2.3) 为了使均方误差控制在O(ε2)内,即要求N=O(ε-2),h=O(ε),从而计算的复杂性即计算成本就是O(ε-3)。通过多层蒙特卡罗模拟方法,在保持偏差不变的情况下计算成本可以减少到O(ε-2(logε)2)。多层蒙特卡罗方法具有便于实现的优点,并且原则上可以与其他的方差减小技术结合使用从而进一步降低计算成本。 多层蒙特卡罗方法扩展了Kebaier[17]的研究,应用了一个有不同步长的几何序列,hl=M-1T,l=0,1,…,L,其中整数M≥2,最小步长hL对应于最初的h。h决定了欧拉离散偏差的大小。这种多重网格,每个格在每个方向上都比前一个格纤细M倍。通过将精细的网格和较粗网格结合,从而既降低了计算成本,也得到了较高的精确度。多层蒙特卡罗方法的本质是即保留与最小步长关联的偏差,但是用较大步长的计算结果降低计算成本,最终减少方差。 2.2 多层蒙特卡罗方法 (2.4) (2.5) 对于l=1,…,L来说,有下式: 因此: (2.6) 由上可知,虽然我们用不同的层数来估计E[f(X)],且每层都有不同的离散误差,最终结果的精度取决于最优的层数L。 (2.7) (2.8) (2.7)式右边的第二项为偏差的平方,假设O(hl)对于每个l来说都是弱收敛,可以得到整个方法的偏差O(hL)=O(M-L),为了得到想要的精度,我们希望误差接近于ε,因此可以得到: L=-logMε=logε-1(logM)-1=O(logε-1) 由上述估计,可以得到多层蒙特卡罗方法整体计算成本近似于: (2.9) 显而易见,当ε→0时,有ε-1≫(logε)2。由此可以看出多层蒙特卡罗方法的计算成本比标准蒙特卡罗(C=O(ε-3))有显著降低。 2.3 偏差估计 (2.10) (2.11) 在后续研究中算法实现中所用的条件是: (2.12) 这保证了基于两个最优步长的残差都在希望的误差范围内。 3.1 多层蒙特卡罗定价巴黎期权的算法思路 算法思路如下: (2.13) (4)如果L≥2,用等式(2.13)来测试收敛性; (5)如果L≤2或者不收敛,令L=L+1并且回到步骤2; 3.2 连续型巴黎期权 假设股票为标的资产,以St表示标的资产价格,K表示执行价格,T表示合约存续期,r表示无风险利率,σ为标的资产波动率,Wt为标准布朗运动。其中St满足以下几何布朗运动(风险中性测度下): dSt=rStdt+σStdWt 由伊藤引理可得: (3.1) 其中Δt=T/m。巴黎期权与欧式期权最大的差异在于巴黎期权具有持续时间D的条款,而标的资产价格路径仍然满足式(3.1)。令τ表示标的资产价格在障碍水平之上(下)连续时间的长度,那么对于向上的障碍,我们可以如下定义τ: τ(t)=t-sup{t′≤t|S(t′)≤B} (3.2) 同理对于向下的障碍,τ为: τ(t)=t-sup{t′≤t|S(t′)≥B} (3.3) 若以向下敲出看涨巴黎期权为例,任取一条标的资产价格路径,此时累计持续时间τ满足(3.3),当τ(t)≥D时,期权敲出,该条路径期权到期支付与欧式期权相同。根据以上讨论再结合标准蒙特卡罗的求解步骤,可以得到连续型向下敲出看涨巴黎期权定价如式(3.4)所示,其样本路径生成和选取方式的具体选取方法见上述的算法步骤。 (3.4) 图1 层数l与方差之间的关系 图1中Pl为标准蒙特卡罗方法的方差,Pl-Pl-1为多层蒙特卡罗方法的方差,由图1中可知,随着l增加,多层蒙特卡罗的方差比标准蒙特卡罗的方差明显减小,这说明多层蒙特卡罗能够明显减少方差。 图2则说明了层数l与每层新增路径条数ΔNl之间的关系,由图2可知,随着层数的增加,每层增加的路径条数相应减少,即相应增加一层,只需要增加ΔNl条路径即可完成计算,因此计算成本也相应的降低。从图2中还可以看出,当ε减小时,每层新增路径数ΔNl是增加的,这是因为当精度提高时,相应的计算成本增加。在此参数下,由多层蒙特卡罗方法计算得出的连续型巴黎期权价格为3.5563。 图2 层数l与每层新增路径条数ΔNl之间的关系 3.3 累计型巴黎期权 (3.5) 同样取S0=30,K=28,B=29,r=0.04,T=1,σ=0.25,D=0.1,ε=0.001,多层蒙特卡罗计算出累计型巴黎期权的价格为3.1846,而使用标准 蒙特卡罗方法计算出的累计型巴黎期权价格为3.2049。图3是采用多层蒙特卡罗方法计算出的累计巴黎期权精度分析中的相关参数。 由图2可知,在精度一定的条件下,随着计算层数l的增加,多层蒙特卡罗方法的方差逐步减小,远小于标准蒙特卡罗方法的方差。并且随着层数l的增加,每层所需计算的新增路径条数ΔNl减少,计算成本也随之明显下降。即在给定的精度条件下,多层蒙特卡罗方法的相应的计算成本远低于标准蒙特卡罗方法。随着精度要求的提高,每层需要新增加的路径条数ΔNl也相应增加,即对精度要求的提高自然增加了计算成本。 图4对比了多层蒙特卡罗方法与标准蒙特卡罗方法的计算成本,由图4可知,在精度都为0.01的情况下,使用标准蒙特卡罗方法的计算成本为10左右,而使用多层蒙特卡罗方法的计算成本为10-1左右,多层蒙特卡罗方法计算成本远小于标准蒙特卡罗方法的计算成本,由此可知使用多层蒙特卡罗方法可以有效地降低计算成本。 3.4 移动窗口巴黎期权 图3 累计巴黎期权的精度分析示意——多层蒙特卡罗 由此可知,移动窗口向下敲出看涨巴黎期权的价格为: (3.6) 图4 多层蒙卡与标准蒙卡计算精度对比分析 移动巴黎期权的多层蒙特卡罗计算结果和相关精度分析与前两种巴黎期权趋势基本相同。移动窗口巴黎期权除了上述参数之外, 还需要一个窗口期 C,这里给定窗口期C=0.2。下面将比较分析采用多层蒙特卡罗方法和标准蒙特卡罗方法计算的三种巴黎期权的价格,从而进一步展示多层蒙特卡罗方法的正确性和优势。 3.5 多层蒙特卡罗方法与标准蒙特卡罗方法计算结果对比 图5中左图为标准蒙特卡罗方法计算得到的巴黎期权价格,右图为由多层蒙特卡罗方法计算得出的巴黎期权价格。由于移动巴黎期权的窗口期等于0.2,因此当徘徊时间D等于0.2时,移动窗口巴黎期权退化为连续型巴黎期权。无论是从图5还是从表2的数值计算结果都表明,这两个期权的价格在D等于0.2是价格曲线是交于一点的,从而侧面验证了多层蒙特卡罗方法计算巴黎期权的正确性。当然这一关系对于标准蒙特卡罗方法也是成立的。由图5中还可以看出,巴黎期权价格趋势基本相同,但是可以清晰看出多层蒙卡计算结果绘出的价格曲线要比标准蒙特卡罗方法所得到的价格曲线平滑很多,说明多层蒙特卡罗方法明显提升了计算的精度和效率。 表1、表2则分别给出了用标准蒙特卡罗方法和多层蒙特卡罗方法计算的三种巴黎期权价格的具体数值结果。 图5 三种巴黎期权的价格对比分析——标准蒙卡和多层蒙卡 表1 标准蒙特卡罗计算的三种巴黎期权价格 表2 多层蒙特卡罗计算的三种巴黎期权价格 下面主要从与标准蒙特卡罗方法的对比总结中阐述多层蒙特卡罗方法的优势。 4.1 计算精度方面的优势 由图6中的上图可知,当标的资产价格路径为100,000条时,采用标准蒙特卡罗方法得到的计算结果仍然在4.6-4.7之间震荡,此时的计算精度大约为0.1,而从图6中的下图对应的多层蒙特卡罗方法来看,在100,000条路径时,相应的精度已达到0.0002范围内,其精确度与起标准蒙特卡罗方法有大幅提升。 图6 多层蒙特卡罗方法与标准蒙特卡罗计算效率比较 因此可知,当计算成本相同的情况下,多层蒙特卡罗方法克服了标准蒙特卡罗计算期权价格存在的收敛性较差的问题,从而能够更快地达到相同的计算精度。 4.2 计算成本方面的优势 在计算精度一定的情况下,标准蒙特卡罗的计算复杂性即计算成本就是O(ε-3)。而对于多层蒙特卡罗方法,计算成本可以减少到O(ε-2(logε)2),降低了半个数量级左右,在计算规模较大时,就可以明显体现出计算成本的优势。图7很好地说明了两种蒙特卡罗方法同等精度条件下计算成本的优劣。 图7 两种蒙特卡罗方法计算成本对比 由此可知,多层蒙特卡罗方法最大的优势在于:在给定的精度条件下,相对标准蒙特卡罗方法,多层蒙特卡罗方法能够有效地将计算成本从O(ε-2(logε)2)降低到O(ε-3);反之,在给定的计算成本条件下,相对标准蒙特卡罗方法,多层蒙特卡罗方法能够更快的收敛到真实值附近。 由于克服了维度诅咒问题,蒙特卡罗方法更适合给强路径依赖期权定价;而多层蒙特卡罗方法能够有效地改进标准蒙特卡罗方法,在给定的精度条件下,有效的降低了计算成本,将计算成本从标准蒙特卡罗方法的O(ε-3)降低到了O(ε-2(logε)2);同时在给定的计算成本条件下,相对标准蒙特卡罗方法,多层蒙特卡罗方法的能够更快地收敛到真实值附近。 但是该算法还有一些不确定性,首先,它并不能保证一定能得到一个值为O(ε2)的均方误差。其次,每个层次的方差估计值的准确度取决于初始样本集的大小。这将是论文未来研究方向。 [1] Chesney M, Jeanblanc-Picqué M, Yor M. Brownian excursions and Parisian barrier options [J]. Advances in Applied Probability, 1997,29(1): 165-184. [2] Haber R J, Schönbucher P J, Wilmott P. Pricing parisian options [J]. The Journal of Derivatives, 1999, 6(3): 71-79. [3] Vetzal K R, Forsyth P A. Discrete Parisian and delayed barrier options: A general numerical approach [J]. Advances in Futures and Options Research, 1999, 10: 1-16. [4] 宋斌, 周湛满, 魏琳, 等. 巴黎期权的 PDE 定价及隐性差分方法研究[J]. 系统工程学报, 2013, 28(6): 764-774. [5] Avellaneda M, Wu Lixin. Pricing Parisian-style options with a lattice method [J]. International Journal of Theoretical and Applied Finance, 1999, 2(1): 1-16. [6] Costabile M. A combinatorial approach for pricing Parisian options [J]. Decisions in Economics and Finance, 2002, 25(2): 111-125. [7] Anderluh J H M. Pricing Parisians and barriers by hitting time simulation [J]. European Journal of Finance, 2008, 14(2): 137-156. [8] 郭冬梅, 宋斌, 汪寿阳, 等. 基于停时模拟的移动窗口巴黎期权的定价[J]. 系统工程理论与实践, 2013, 33(3): 577-584. [9] 谭英双, 衡爱民, 龙勇, 等. 模糊环境下不对称企业的技术创新投资期权博弈分析[J]. 中国管理科学, 2011, 19(6): 163-168. [10] Kwok Y K, Lau K W. Pricing algorithms for options with exotic path-dependence [J]. Journal of Derivatives, 2001, 9(1): 28-38. [11] Boyle P P, Broadie M, Glasserman P. Monte Carlo methods for security pricing [J]. Journal of Economic Dynamics and Control, 1997, 21(8): 1267-1321. [12] Bernard C, Boyle P. Monte Carlo methods for pricing discrete Parisian options [J]. The European Journal of Finance, 2011, 17(3): 169-196. [12] Joy C, Boyle P P, Tan K S. Quasi-Monte Carlo methods in numerical finance [J]. Management Science, 1996, 42(6): 926-938. [13] Giles M B. Multilevel Monte Carlo path simulation [J]. Operations Research, 2008, 56(3): 607-617. [14] Giles M B, Higham D J, Mao Xuerong. Analyzing multi-level Monte Carlo for options with non-globally Lipschitz payoff [J]. Finance and Stochastics, 2009, 13(3): 403-413. [15] Giles M B, Waterhouse B J. Multilevel quasi-Monte Carlo path simulation [J]. Advanced Financial Modeling, Radon Series on Computational and Applied Mathematics, 2009,(8): 165-181. [16] Primozic T. Estimating expected first passage times using multilevel Monte Carlo algorithm [D]. Oxford:Oxford University, 2011. [17] Kebaier A. Statistical Romberg extrapolation: A new variance reduction method and applications to option pricing [J]. The Annals of Applied Probability, 2005, 15(4): 2681-2705. Pricing Parisian Option by Multi-level Monte Carlo Method SONG Bin1, LIN Ze-fu1, ZHANG Bing-jie2 (1.School of Management Science and Engineering,Central University of Finance and Economics,Beijing 100081,China;2.School of Management,Beihang University,Beijing 100191,China) Parisian option is a complex path-dependent option extended from the barrier options, which allows the holder buy or sell a certain underlying asset at a pre-specified price under the condition that underlying asset price above or below a given level of a continuous or cumulative occupation time before maturity. The numerical methods for pricing Parisian option include binomial tree method, finite difference method and Monte Carlo method. Compared with other numerical methods, Monte Carlo method is more flexible and easy to implement and improve; moreover, its estimation error and convergence speed has stronger independence with the dimensions of the problem to be solved, and thus can solve the target variable of high-dimensional derivative securities pricing better.In this paper the Parisian option is priced using the Monte Carlo method, and improves the standard Monte Carlo algorithm is improved to multi-level Monte Carlo algorithm. Our research results show that under the given accuracy, multi-level Monte Carlo algorithm can reduce the calculation costs fromO(ε-3) to O(ε-2(logε)2) comparing with the standard Monte Carlo method. On the other hand, under given calculation cost, multi-level Monte Carlo method can converge to the true value faster comparing with standard Monte Carlo method. Applying this method to Parisian option pricing not only expanses the choice scope of Parisian options’ numerical algorithms, but also improves the precision of Parisian option pricing, and lays a certain foundation for Parisian options’ application in the domestic market. Parisian option; standard Monte Carlo method; multi-level Monte Carlo method;computation cost 1003-207(2016)02-0011-08 10.16381/j.cnki.issn1003-207x.2016.02.002 2014-12-16; 2015-09-17 教育部人文社会科学研究规划基金(14YJA790048);国家自然科学基金资助青年项目(11301560);国家自然科学基金资助青年项目(71301173) 简介:宋斌(1971-),女(汉族),山西人,中央财经大学管理科学与工程学院投资系,系主任,研究方向:复杂衍生产品的定价与数值计算、倒向随机微分方程在经济与金融中的应用、利率市场微观结构与订单簿建模、利率期限结构建模,E-mail:selviasong@163.com. F830.9 A


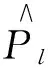


3 多层蒙特卡罗方法的数值分析







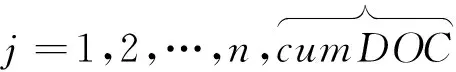

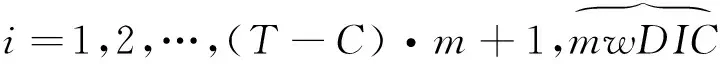
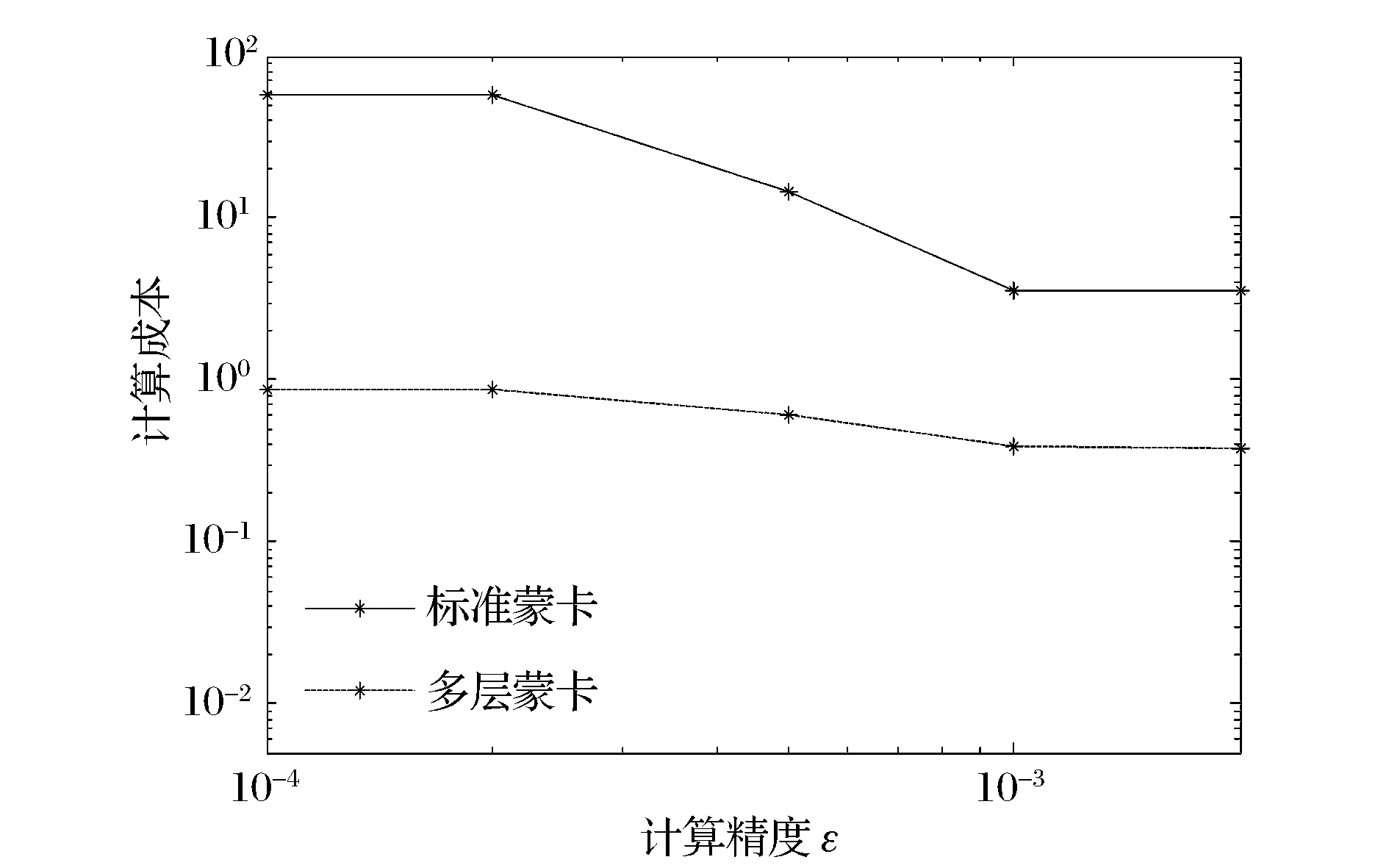
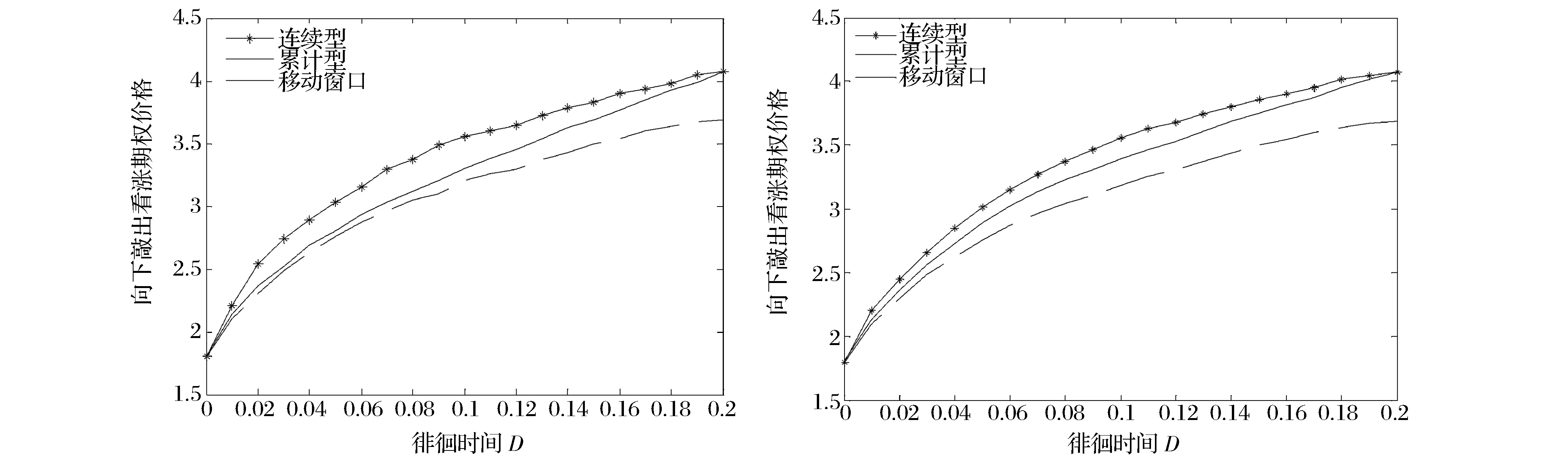


4 多层蒙特卡罗方法的优势


5 结语

