三元效率区间下决策单元的全局绩效评价

范建平，陈 静，吴美琴，田 璇

(1.山西大学经济与管理学院，山西 太原 030006；2.山西大学科学评价研究中心，山西 太原 030006)



三元效率区间下决策单元的全局绩效评价

范建平1,2，陈 静1，吴美琴1，田 璇1

(1.山西大学经济与管理学院，山西 太原 030006；2.山西大学科学评价研究中心，山西 太原 030006)

针对现实生活中投入产出数据的不确定性，许多学者提出从乐观和悲观角度计算决策单元的效率区间，但每个效率区间的上、下界值都是决策单元表现的两种极端情况。本文通过引入心态指标衡量决策者的偏好，获得了一个最有可能的效率值，它与上界值、下界值共同组成了三元效率区间。然后改进了两级排序方法：提出了三元有向距离指数，为所有决策单元获得全序化结果。本文引用前人文中的数例验证了该方法是一种更为精确、可全序化的评价、决策方法，可广泛应用于效率测评中。

数据包络分析；三元效率区间；乐观效率；悲观效率；三元有向距离指数

1 引言

数据包络分析(Data Envelopment Analysis，DEA)是基于1978年Charnes等[1]首次提出经典模型之后发展起来的，它是一种线性非参数模型，用来评价一组具有相同的多投入多产出的决策单元(Decision-Making Units，DMUs)的相对效率。由于DEA无需知道决策单元真实的生产运作函数，相对于其他效率评价方法具有一定的优势，所以它在各个领域中得到了广泛的应用，比如银行业[2-3]、奥运会[4]、环境测评[5]、教育系统[6]、制造业[7]、城市创新能力[8]、电力行业[9]等.

传统的DEA模型[1,10]评价每个决策单元的相对效率时，获取的投入、产出权重对每个决策单元自己是最有利的，这种评价方法是从乐观角度进行的，获得的相对效率称之为最好相对效率或乐观效率。随后，Parkan等人[11]提出了从悲观角度考量决策单元绩效的方法，这时获得的对被评价决策单元最不利的效率被称之为最坏相对效率或悲观效率。乐观效率和悲观效率测评了每个DMU两种完全不同情形下的效率，为了准确的衡量决策单元的全局绩效，我们必须同时考虑乐观和悲观效率。同时考虑每个决策单元乐观和悲观效率的方法，我们称之为“双前沿面分析法”。

使用双前沿面分析法一般需要考虑两个步骤。第一个步骤为如何计算效率区间。最先提出从乐观和悲观角度去评价每个决策单元全局绩效的是Doyle等人[2]，在他们的研究中，悲观效率作为下界，乐观效率作为上界，共同组成了效率区间。Entani等[3]提出了新的模型去计算效率区间，但是它有两个明显的缺点：一是在计算效率区间的下界时只利用了一个投入和一个产出，导致了信息缺失，二是使用了可变生产前沿面，使得计算的效率区间不具有可比性。为了改进这些缺点，Wang Yingming等人[4]提出了一组有界DEA模型，通过引入一个虚拟的非理想DMU和理想DMU去测评乐观和悲观效率，最大程度的利用了投入、产出信息。然而当每项产出或者投入中都有一个数据为零时，有界DEA模型便无法获得效率区间，于是Azizi等[15-16]提出了改进的有界模型，使用乐观效率和悲观效率测评了决策单元的全局绩效。第二是如何整合效率区间使之成为决策单元全局绩效的排序指标。Wang Yingming等[17]将两种效率的几何平均效率作为排序准则，它比只考虑其中一种效率更为全面。Amirteimoori等[18]基于有效和无效前沿面提出了理想和非理想指标，即最大化被评价的DMU到有效和无效前沿面的加权距离。陆志鹏等[19]将决策单元的变量区间划分为若干个子区间，对各个区间上决策单元DEA效率进行集结，得到综合效率区间，作为决策单元的效率评价的基准。Wu Jie等[20]结合了DEA和TOPSIS法，通过优化模型将权重的主观赋值变为客观计算，避免了由于人为因素引起的权重偏差。

不可否认，无论是从乐观还是悲观角度，效率区间测评了DMU的两种极端情况，上述提到的任何一种效率评价方法都没有考虑决策者(Decision Makers，DMs)的偏好。的确，现有的研究要么关注效率的计算过程要么关注其应用领域，很少考虑决策者的个人偏好。这里的偏好是指：在乐观情形下，决策者对决策单元的效率值呈乐观态度，除了乐观效率的最大值和最小值，我们更应该计算一个最有可能的值。同理，我们也可获得最有可能的悲观效率值。本文将反映决策者不同期望偏好的心态指标引入乐观和悲观效率中，获得决策单元的三元效率区间。然后提出了区间数据两级排序决策全序化的一种方法：三元有向距离指数，解决优势度方法排序后出现多于一个决策单元排在同一位置的现象。

2 乐观和悲观效率模型

2.1 乐观效率区间和悲观效率区间

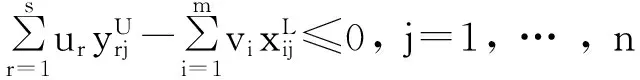
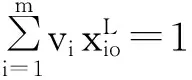
(1)

ur,vi≥ 0, r=1, … ,s ; i=1, … ,m

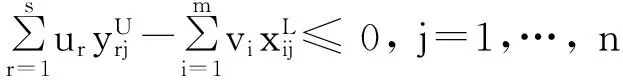
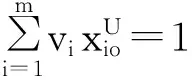
(2)

ur,vi≥0,r=1, … ,s ; i=1, … ,m.

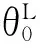
Azizi等[22]于2011年提出评价DMUo相对于其他决策单元的悲观效率线性计算模型：

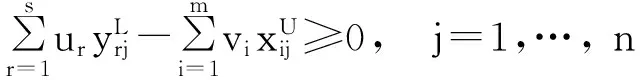
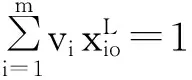
(3)

ur，vi≥0, r=1, …,s;i=1, … ,m

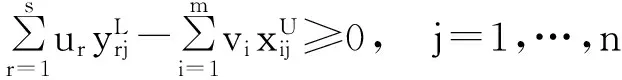
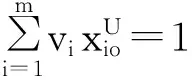
(4)

ur，vi≥0, r=1, …,s; i=1, …,m

2.2 心态指标

定义1：假定一个区间数a ∈[a-,a+]， Ma为区间数的期望值：Ma=(a-+a+)/2，Wa代表区间宽度：Wa=(a+-a-)/2，我们在[0,1]上定义函数[23]: Fa(α): [0,1]→[a-,a+]：

Fa(α)=Ma+ (2α-1) Wa，

α 称为决策者的心态指标，Fa(α)是 [0,1]区间上的单调递增函数，且

(1)当α=0时，Fa(α)=a-，则称α 为下限指标，表明决策者呈悲观心态；

(2)当α=1时，Fa(α)=a+，则称α 为上限指标，表明决策者呈乐观心态；

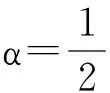
2.3 三元效率区间

现在我们提出加入心态指标的三元效率区间模型。

s.t. 与模型(1)约束相同

(5)

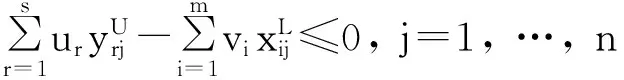
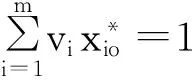
(6)

ur，vi≥0, r=1, …,s; i=1, …,m

s.t. 与模型 (2) 约束相同

(7)

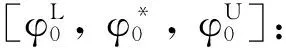
s.t. 与模型 (3) 约束相同

(8)

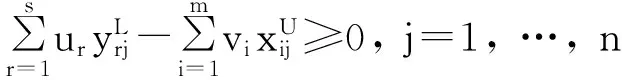
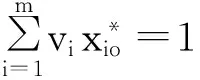
(9)

ur，vi≥0, r=1, … ,s; i=1, … ,m

s.t. 与模型 (5) 约束相同

(10)

3 基于优势度和有向距离指数的两级排序方法

3.1 序信息系统中的优势度和有向距离指数

定义2[24]：称四元组S=(U，AT，V，f)为区间信息系统(IIS)，其中U为有限非空方案集，AT为有限非空属性集，V =∪a∈ATVa，Va是属性a的值域，f: U×AT→V是一个信息函数，表示对于任意的a∈AT, x∈U都有f(x，a)∈Va。这里，方案x在属性a下的值Va为区间数，记做：

f (x, a) =[aL(x), aU(x)]={p | aL(x) ≤p≤aU(x), aL(x), aU(x)∈R}。

若所有的属性均是有序型属性，即所有属性的取值可以按照收益型或者成本型偏好排序，则称区间信息系统S=(U，AT，V，f)为区间序信息系统(IOIS)。

在区间序信息系统中，任意属性a的取值都是可以通过优势关系a来表示的，xay表示在属性a上x优于y。同理，xAy ⟺ ∀a∈A, xay。 基于上述描述，我们可以通过引入优势关系来定义优势类。在区间序信息系统中，关于属性集A ⊆ AT上有y优于x，即yAx，可以通过来定义：

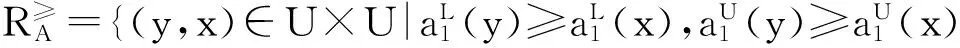
其中A=A1∪A2，A1为收益型属性集，A2为成本型属性集。

我们现在考虑区间数据基于优势度排序方法。

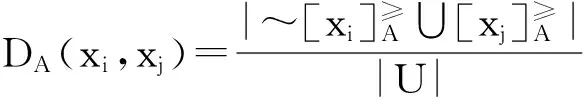
(11)

当(xi, xj) ∈U×U时，基于优势关系可以获得在属性集A上的优势关系矩阵，通过这个矩阵，可以得到方案xi的整体优势度：

(12)

由上可得，DA(xi)的取值越大，方案xi的表现越好。整体优势度DA(xi)即可用来给论域中所有方案进行全局排序。

无论在数例还是实证研究中，基于优势度排序后，常常发现两个或多于两个的方案排在同一位置，并且排序越靠前的方案越容易出现这种并列现象。为了获得方案的全序化，宋鹏[25]提出了有向距离指数作为二级排序方法，它关注于区间数据的取值，是一种更为精确的测量方案xi相对于xj优劣程度的方法。

定义4: f (xi,a)=[aL(xi), aU(xi)]，f(xj,a)=[aL(xj), aU(xj)]为给定的区间数据，在属性a上，方案xi相对于xj的有向距离指数定义为：

(13)

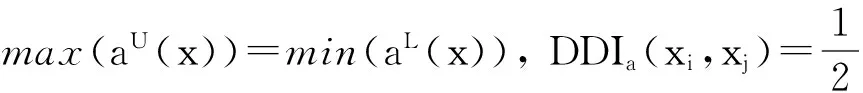
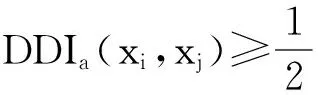
将DDIa(xi,xj)扩展到某一属性集上，属性集A上的有向距离指数定义为：

其中，A∈AT，|A|为属性集里属性个数。

为了获得全序结果，需要获得方案的整体有向距离指数。将方案xi的整体有向距离指数定义为：

整体有向距离指数DDIA(xi)越大，方案 xi排序越好。

3.2 三元有向距离指数

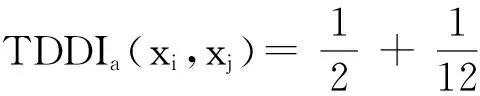
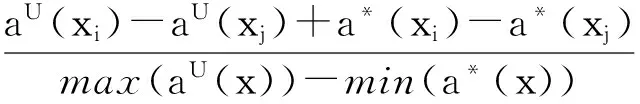
(14)

其中，max(aU(x))=max{aU(x1), aU(x2), … ,aU(x|U|),}，max(a*(x))=max{a*(x1), a*(x2), … ,a*(x|U|),}，min(a*(x))=min{a*(x1), a*(x2), … ,a*(x|U|)}，min(aL(x))=min{aL(x1), aL(x2), … ,aL(x|U|)}，xi, xj∈U。且有：

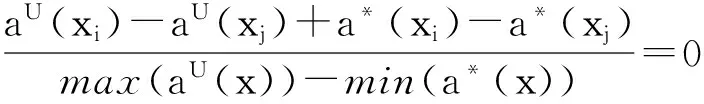
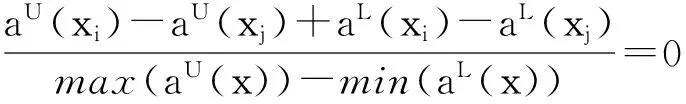
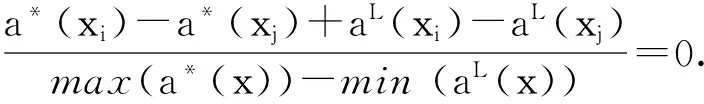
TDDIa(xi,xj) 仅仅考虑了方案 xi相对于xj在属性a上的相对优劣程度，同样我们将TDDIa(xi,xj) 扩展到属性集A上，属性集A 上的三元有向距离指数定义为：

(15)

其中，A ∈ AT，|A|为属性集里属性个数。

同理，方案xi的整体三元有向距离指数定义为：

(16)

这样，每一方案总体优劣的评价则可以通过任意方案两两之间的比较来获得。整体三元有向距离指数TDDIA(xi)越大，方案 xi排序越好。

4 数据结果及分析

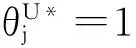
根据优势度，给出所有决策单元关于乐观效率的排名。首先，基于优势关系，找出每个决策单元的优势类。

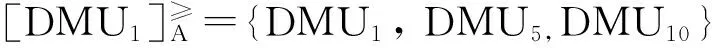
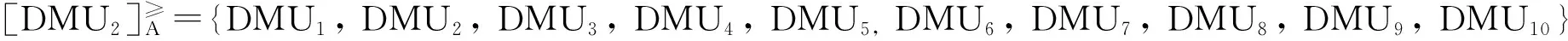
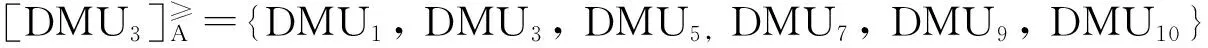
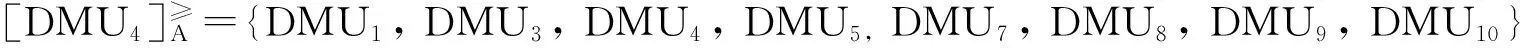
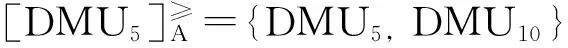
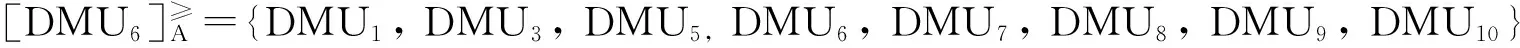
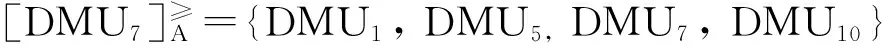
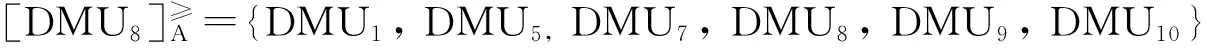
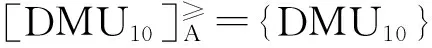
然后，根据公式(11)计算每个决策单元的优势度，可以得到优势度矩阵，如表2所示。利用公式(12)和优势度矩阵，计算得到每个决策单元的全局优势度。

DA(DMU1)=87/90, DA(DMU2)=42/90,

DA(DMU3)=74/90, DA(DMU4)=59/90,

DA(DMU5)=89/90, DA(DMU6)=59/90,

DA(DMU7)=83/90, DA(DMU8)=75/90,

DA(DMU9)=83/90, DA(DMU10)=1

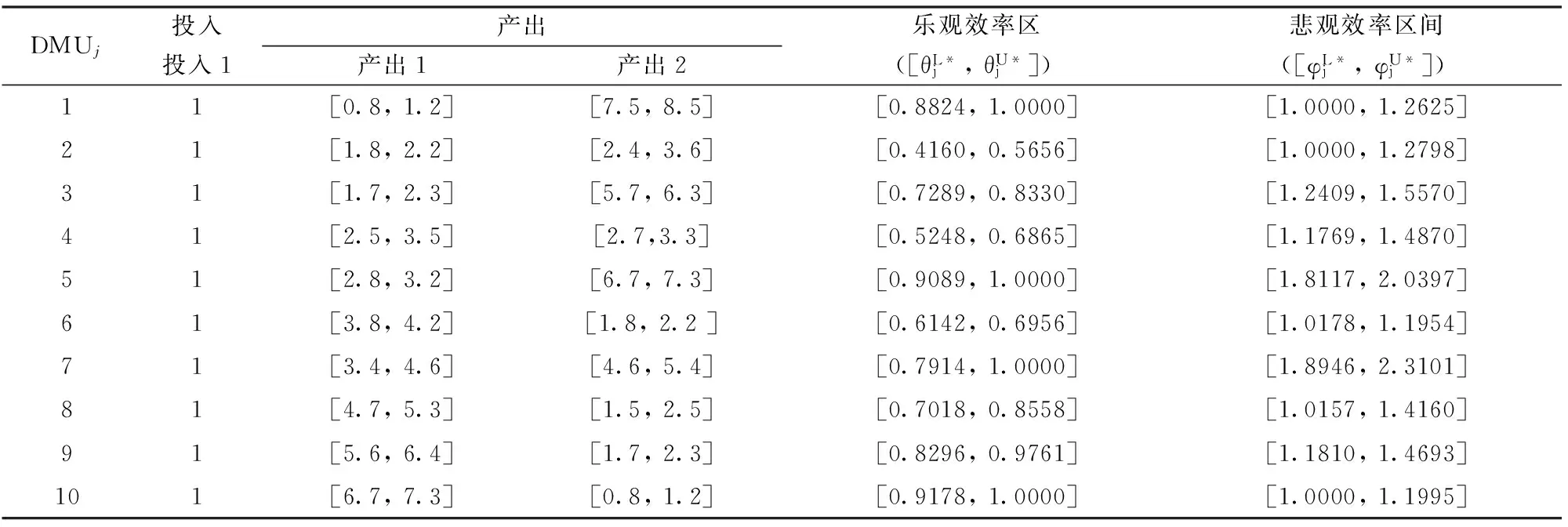
表1 七个制造企业的投入产出数据及效率

表2 决策单元间的优势度矩阵

根据全局优势度的大小，决策单元的排名如下：

DMU10DMU5DMU1DMU3DMU8DMU2。

正如上文中提到的，不止一个决策单元会排在相同的位置，本例中DMU7和DMU9、DMU4和DMU6排在相同位置。现在使用有向距离指数将这些决策单元区别开来。

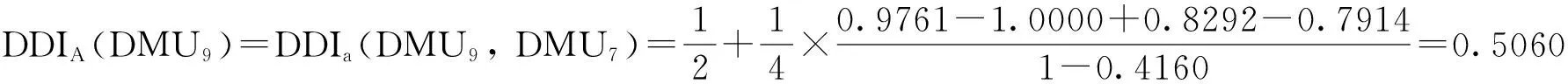
DDIA(DMU7)=DDIa(DMU7, DMU9)=1 - DDIa(DMU9, DMU7)=0.4940，

DDIA(DMU9)>DDIA(DMU7)，所以DMU9DMU7。同理可得DMU6DMU4。

七个决策单元在乐观效率区间下的排序为：DMU10DMU5DMU1DMU9DMU7DMU3DMU8DMU6DMU4DMU2，与我们事前估计的一样，这个排序结果和使用Wang Yingming等[26]提出的偏好度排序方法得出的结果是一致的。因此基于上述描述，全局优势度和有向距离指数是一种合理有效的排序方法，并且能够提供全序化结果。

现在引入反应决策者偏好的心态指标去计算每个决策单元的三元效率区间。在乐观情形下，将投入 α 值设为0.3，产出 α 值设为0.8。在悲观情形下，将投入 α 值定为0.8，产出 α 值定为0.3(投入产出的 α 值是随决策者的期望偏好变化的，决策者可自行设定)。引入心态指标后七个决策单元的乐观和悲观三元区间数据如表3所示，分别计算的效率区间如表4。

基于三元乐观效率区间给决策单元排序时，每个决策单元的优势类为：

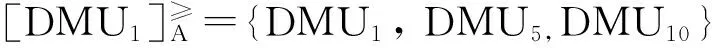
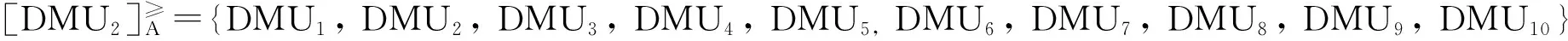
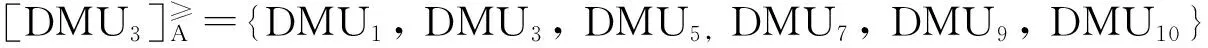
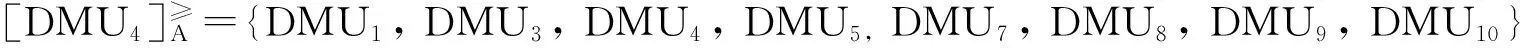
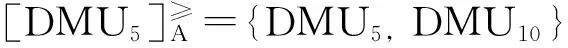
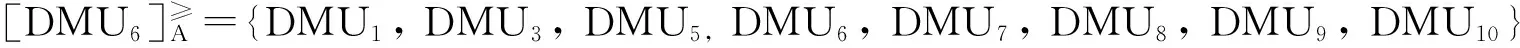
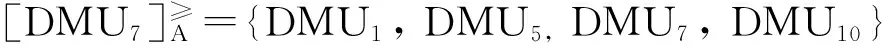
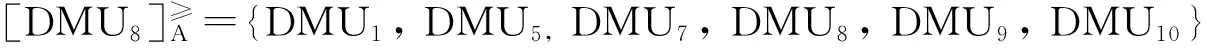
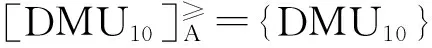
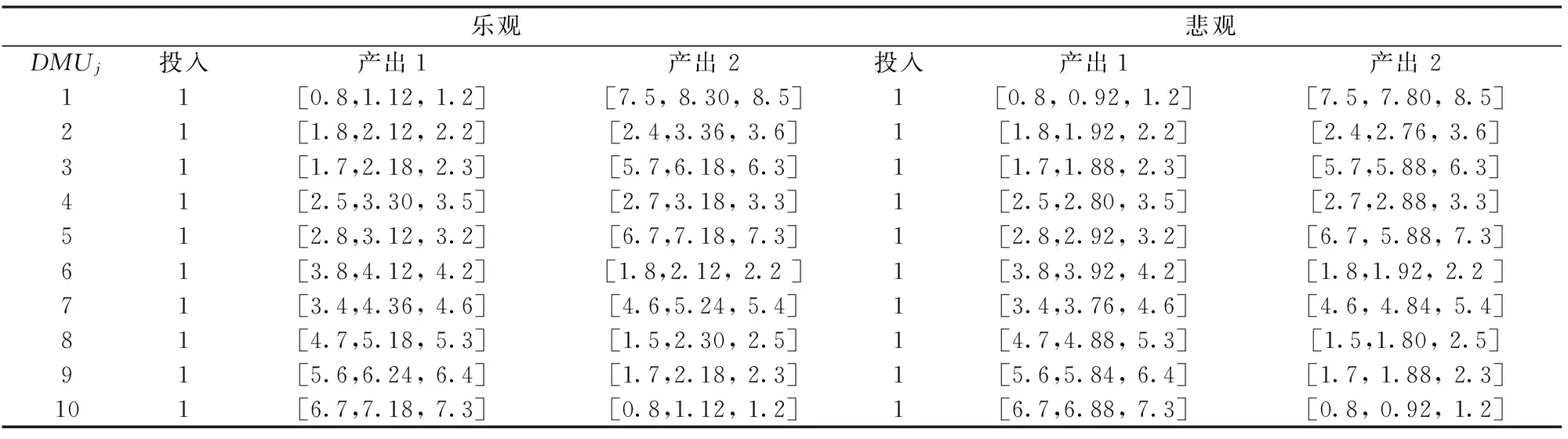
表3 决策单元乐观、悲观情况下投入产出数据

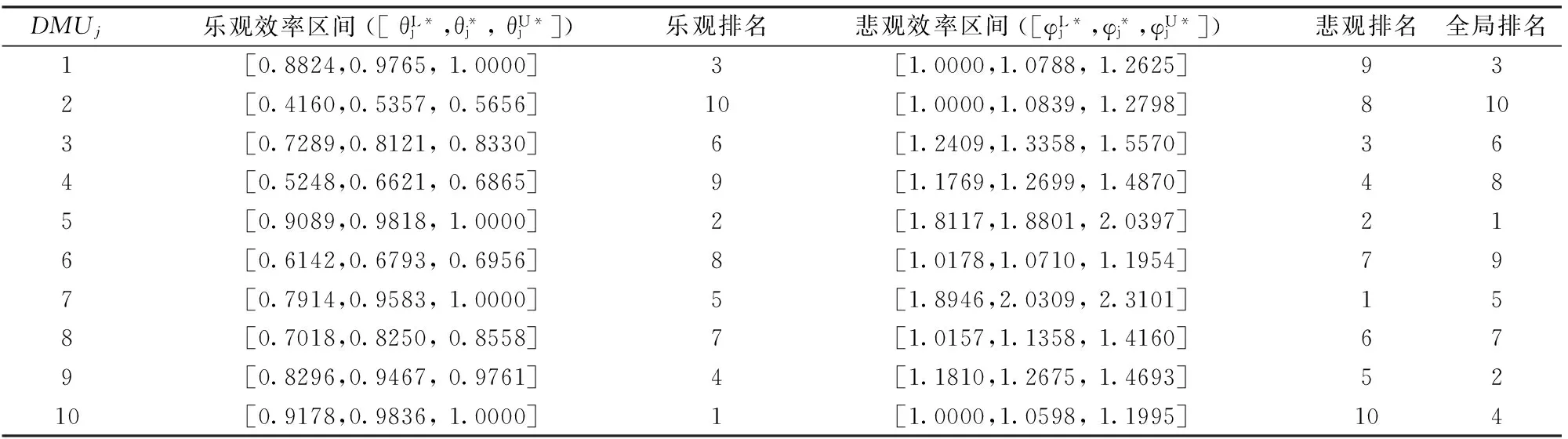
表4 决策单元的三元乐观效率区间和三元悲观效率区间

我们会发现三元乐观效率区间上的优势类与二元乐观效率区间上是一致的，所以用优势关系给决策单元一级排序之后获得的顺序与上述顺序也是一致的，即为：

DMU10DMU5DMU1DMU3DMU2

现在使用三元有向距离指数将获得一样排名的决策单元区别开来：

TDDIA(DMU7)=TDDIa(DMU7, DMU9)=1- TDDIa(DMU9, DMU7)=0.6745

TDDIA(DMU9) ≥ TDDIA(DMU7)，所以 DMU9DMU7，同理可得：DMU6DMU4。

所以在三元乐观效率区间下，决策单元排名为：DMU10DMU5DMU1DMU9DMU7DMU3DMU8DMU6DMU4DMU2。与在二元乐观效率区间的结果相比稍有不同，容易发现DMU7和DMU9排序位置互换。我们称这种排序结果的变化是因为加入了反映决策者偏好的最有可能的效率值引起的。同理，我们可以获得决策单元在三元悲观效率区间下的全序排名，结果为：DMU7DMU5DMU3DMU4DMU9DMU8DMU6DMU2DMU1DMU10。

三元乐观效率区间和三元悲观效率区间下的排序是对决策单元在两种极端情况下的测评，这两种排序结果是完全不同的，如表4第三和第五列所示。既然这两种情况是彼此冲突、互不包容的，那么任何一种只考虑其中一种情况的测评方法一定是片面的、没有说服力的。为了对每个决策单元进行全局绩效测评，将三元乐观效率和三元悲观效率看做决策单元的两个属性，这种方法既同时考虑了两种极端效率，也替代了其他论文中将这两种效率整合成一个效率的方法。计算优势度和整体三元有向距离指数后，七个决策单元的全局排序为：DMU5DMU9DMU1DMU10DMU7DMU3DMU8DMU4DMU6DMU2。

需要说明的是：我们不可能总把乐观有效的决策单元排在乐观非有效决策单元的前面，当将悲观效率考虑进来时，一些乐观有效的决策单元就会获得比其他决策单元更低的排名。如本例中，DMU1、DMU10是乐观有效的，但也是悲观无效的，在全局排序中，DMU9排在了他们前面。

5 结语

在实际应用中，由于观测与统计误差(如经营成本的变动、利润的估计等问题)、信息不完全(如市场或企业信息的不确定性)及实际问题的局限性等原因，往往存在着区间数据的情形。使用DEA区间效率测评具有区间数据的决策单元的绩效是当下使用越来越广泛的方法，本文不仅测评了乐观和悲观情形下效率区间的上界值和下界值，更多的考虑了决策者期望偏好下最有可能的效率值。通过将心态指标引入乐观和悲观效率中，获得了关于每个决策单元的三元乐观效率区间和三元悲观效率区间去评价他们的全局绩效。基于全序化特点和更精确的刻画方案间的优劣程度，我们提出了三元有向距离指数，作为第二级排序方法解决了多于一个决策单元排在同一位置的现象。因此，当决策单元数的数据为区间型、或由于模糊不确定性导致的数据缺失等问题出现时，可应用本文方法进行决策单元的测评和排序。

[1] Charnes A, Cooper W W, Rhodes E. Measuring the efficiency of decision making units[J]. European journal of operational research, 1978, 2(6): 429-444.

[2] 王赫一,张屹两.两阶段DEA前沿面投影问题研究—兼对我国上市银行运营绩效进行评价[J].中国管理科学,2012,20(2)：114-120.

[3] Yang Xiaopeng, Morita H. Efficiency improvement from multiple perspectives: An application to Japanese banking Industry[J]. Omega, 2012, 41(3): 501-509.

[4] Azizi H, Wang Yingming. Improved DEA models for measuring interval efficiencies of decision-making units[J]. Measurement, 2012, 46(3): 1325-1332.

[5] 汪克亮,杨宝臣,杨力.中国省际能源利用的环境效率测度模型与实践研究[J].系统工程,2011,29(1):8-15

[6] Azizi H. A note on data envelopment analysis with missing values: an interval DEA approach[J]. The International Journal of Advanced Manufacturing Technology, 2013,66(9):1817-1823.

[7] 赵萌.中国制造业生产效率评价：基于并联决策单元的动态DEA方法[J].系统工程理论与实践，2012,32(6)：1251-1260.

[8] 杜娟,霍佳震.基于数据包络分析的中国城市创新能力评价[J].中国管理科学,2014,22(6):85-93.

[9] Cook W D, Zhu J. Within-group common weights in DEA: An analysis of power plant efficiency[J]. European Journal of Operational Research, 2007, 178(1): 207-216.

[10] Banker R D, Charnes A, Cooper W W. Some models for estimating technical and scale inefficiencies in data envelopment analysis[J]. Management science, 1984, 30(9): 1078-1092.

[11] Parkan C, Wang Yingming. The worst possible relative efficiency analysis based on inefficient production frontier[R]. Working Paper, Department of Management Sciences, City University of Hong Kong, 2000.

[12] Doyle J R, Green R H, Cook W D. Upper and lower bound evaluation of multiattribute objects: Comparison models using linear programming[J]. Organizational Behavior and Human Decision Processes, 1995, 64(3): 261-273.

[13] Entani T, Maeda Y, Tanaka H. Dual models of interval DEA and its extension to interval data[J]. European Journal of Operational Research, 2002, 136(1): 32-45.

[14] Wang Yingming, Yang Jianbo. Measuring the performances of decision-making units using interval efficiencies[J]. Journal of Computational and Applied Mathematics, 2007, 198(1): 253-267.

[15] Azizi H, Wang Yingming. Improved DEA models for measuring interval efficiencies of decision-making units[J]. Measurement, 2013, 46(3): 1325-1332.

[16] Azizi H, Jahed R. Improved data envelopment analysis models for evaluating interval efficiencies of decision-making units[J]. Computers & Industrial Engineering, 2011, 61(3): 897-901.

[17] Wang Yingming, Chin K S, Yang Jianbo. Measuring the performances of decision-making units using geometric average efficiency[J]. Journal of the Operational Research Society, 2006, 58(7): 929-937.

[18] Amirteimoori A. DEA efficiency analysis: Efficient and anti-efficient frontier[J]. Applied mathematics and Computation, 2007, 186(1): 10-16.

[19] 陆志鹏,王洁方,刘思峰,等.区间DEA模型求解算法及其在项目投资效率评价中的应用[J].中国管理科学,2009,17(4):165-169.

[20] Wu Jie, Sun Jiasen, Song Malin, et al. A ranking method for DMUs with interval data based on dea cross-efficiency evaluation and topsis[J]. Journal of Systems Science and Systems Engineering, 2013,22(2): 191- 201.

[21] Wang Yingming, Greatbanks R, Yang Jianbo. Interval efficiency assessment using data envelopment analysis[J]. Fuzzy sets and Systems, 2005, 153(3): 347-370.

[22] Azizi H, Ajirlu H G. Measurement of the worst practice of decision-making units in the presence of non-discretionary factors and imprecise data[J]. Applied Mathematical Modelling, 2011, 35(9): 4149-4156.

[23] 胡启洲，张卫华. 区间数理论研究及其应用[M]. 北京：科学出版社. 2010.

[24] Qian Yuhua, Liang Jiye, Dang Chuangyin. Interval ordered information systems[J]. Computers & Mathematics with Applications, 2008, 56(8): 1994-2009.

[25] 宋鹏. 基于序化机理的稳健型股票价值投资研究[D]. 太原：山西大学, 2012.

[26] Wang Yingming, Luo Ying, Liang Liang. Fuzzy data envelopment analysis based upon fuzzy arithmetic with an application to performance assessment of manufacturing enterprises[J]. Expert systems with applications, 2009, 36(3): 5205-5211.

第十八届中国管理科学学术年会征文通知

第十八届中国管理科学学术年会将于2016年11月11日-13日在西安交通大学召开，欢迎广大专家学者、科技和教育工作者积极投稿并参加会议。

主办单位：中国优选法统筹法与经济数学研究会 西安交通大学

中国科学院科技政策与管理科学研究所 《中国管理科学》编辑部

支持单位：陕西省科学技术厅 陕西省发展和改革委员会

承办单位：西安交通大学管理学院

会议主题：大数据驱动的管理创新

征文范围：

优选法与优化管理 统筹法与项目管理 经济数学与低碳经济

大数据技术与方法 数据驱动的过程管理决策 健康管理与大数据医疗

金融工程与风险管理 工业工程与运作管理 信息系统与商务智能

物流与供应链管理 营销工程与服务科学 战略管理与认知决策

数据挖掘与知识管理 人力资源与组织绩效管理 创业与小微企业管理

安全与应急管理 资源型产业发展模式 能源与环境管理

公共管理与复杂系统管理 战略型新兴产业与产业金融 企业管理创新理论与实践

大数据与智慧城市(智慧交通、智慧养老、智慧社区) 大数据金融产业研究

征稿要求：

▲ 未在其它学术会议、论文集和刊物上公开发表过。

▲ 文章具体格式可参照《中国管理科学》近期期刊。

▲ 来稿篇幅要求5-8页(5页以内版面费600元，超过5页每增加一页加收版面费150元)。

▲来稿注明：征文类别(从征文范围中选择一个接近的类别填写)、作者简介、单位、通讯地址、邮编、联系电话、E-mail地址 。

截稿日期：2016年6月30日

录用通知：2016年8月15日

论文出版：

出版《中国管理科学》专辑(已被CNKI数字图书馆全文收录(www.cnki.net))，以国家正式出版物的方式出版发行，书中将收录通过评审录用的论文。并在会前将所有录用论文的长摘要编辑成册《第十七届中国管理科学学术年会论文摘要》 。

大会设优秀论文报告奖：

会议论文通过评审录用后可参加本届年会专题会议的交流评议，获《优秀论文报告奖》的论文将颁发获奖证书并安排在《中国管理科学》正刊发表，直接列入2017年刊登计划。

会议具体情况请登陆中国优选法统筹法与经济数学研究会网站:www.scope.org.cn;中国管理科学网站:www.zgglkx.com及中国学术会议网站：www.zgglkxnh.conf.cnki.net 。

大会秘书处:

联 系 人：傅继良、张玲 E-mail：shuangfa@casipm.ac.cn联系电话：010-62542629

西安交通大学联系人：吕文静、贾峰菊E-mail：jia_fj@mail.xjtu.edu.cn电话：029-82665096

中国优选法统筹法与经济数学研究会

2016年2月3日

Overall Performance Evaluation for DMUs with Ternary Efficiency Interval

FAN Jian-ping1,2, CHEN Jing1, WU Mei-qin1, TIAN Xuan1

(1.School of Economics and Management, Shanxi University, Taiyuan 030006,China；2.Research Center for Science Evaluation，Shanxi University, Taiyuan 030006,China)

To deal with the uncertainty of the data for input and/or output in the real world, many experts presented efficiency interval to evaluate the performance for each DMU from optimistic and pessimistic views. Undeniably, the lower and upper bound of the efficiency interval are two extremes of each DMU performance. In this paper, the preference of the decision makers are considered by introducing the attitude index to get the most probable efficiency value, which with the lower and upper bound constitutes the ternary efficiency interval. Then ternary directional distance index is proposed, improving the two-grade ranking method, to get a full ranking for all DMUs. The illustrative example shows this method is more precise and widely used in efficiency evaluation and decision-making field.the effectiveness and practicability of the proposed method.

data envelopment analysis；ternary efficiency interval；optimistic efficiency；pessimistic efficiency；ternary directional distance index

1003-207(2016)02-0153-09

10.16381/j.cnki.issn1003-207x.2016.02.019

2013-12-01；

2014-12-25

简介：范建平(1975- )，男(汉族)，山西武乡人， 山西大学经济与管理学院，博士，副院长，研究方向：预测、评价与决策,E-mail:fjp@sxu.edu.cn.

C93

A