基于微分博弈的供应链质量协调研究

洪江涛, 黄 沛

(1上海对外经贸大学国际经贸学院，上海 201620; 2.复旦大学管理学院，上海 200433)



基于微分博弈的供应链质量协调研究

洪江涛1,2, 黄 沛2

(1上海对外经贸大学国际经贸学院，上海 201620; 2.复旦大学管理学院，上海 200433)

文章以一个制造商和一个供应商所构成的两级供应链为研究对象，应用微分博弈的方法分析了四种不同的质量管理博弈情形下，制造商和供应商的最优质量管理策略、收益和整条供应链的总收益。研究结果表明，当制造商和供应商的收益分配比满足一定条件时，从Nash非合作质量管理博弈情形，到弱激励Stackelberg博弈情形，再到强激励Stackelberg博弈情形，最后到合作质量管理博弈情形，对于制造商、供应商以及整个供应链系统来说都是一种帕累托改进。所以，合作质量管理博弈情形是供应链质量管理所追求的最理想的情形，为了有效促进该情形的实现，文章应用Nash讨价还价模型对该情形下合作双方关于供应链系统的剩余利润分配进行了分析。最后，在对一家电风扇制造商的供应链进行调查来获得仿真数据的基础上，通过算例分析验证了理论推导的结果。

供应链；质量控制；质量改进；微分博弈；激励

1 引言

近年来，各大公司频频爆出供应链质量管理问题。先是2005年苏丹红事件，涉及企业包括世界跨国公司亨氏、肯德基等，在2008年引起社会广泛关注的“三鹿”奶粉事件， 2010年年初闹的沸沸扬扬的丰田汽车“召回门”事件，以及近两年来众多食品企业的“明胶”问题，都对企业的供应链质量管理敲响了警钟。在这种背景下，供应链质量管理对企业来说，显得尤为重要，因为它贯穿于整个供应链中，通过和供应商建立相互合作关系来实现质量管理的改善以及企业整体绩效的提高，这种关系不仅惠及合作双方，更有利于整个供应链水平的提升[1]。而这种有效的质量合作关系的建立主要依赖于供应链上成员企业间高效的质量协调机制，本文的研究视角正基于此，研究将以传统的两级供应链为例，应用微分博弈的方法来探讨如何在供应链上建立最佳的质量协调机制。

在传统的质量管理文献中，质量管理和质量控制主要是运用统计控制技术(如控制图、方差检验等)来进行研究的，质量问题也被当作一人决策问题，即供应商以最小的成本来达到事先设定的质量水平。然而，在供应链环境下，供应链双方均具有自主决策的能力和意愿，且双方自主决策的相关策略参数均不被对方所观测，于是，供应链质量管理的核心是供应链质量协调。现有供应链质量协调的研究主要围绕供应链双方非合作和合作两种情形展开[2]。

非合作情形下的研究主要关注的是供应链双方的质量协调策略的选择，研究的焦点主要放在供应链双方的投资、生产和检验等策略的制定[3-7]。例如：Hsieh和Liu Yute[3]调查了传统两级供应链上供应商和制造商在四种不同程度信息披露的非合作博弈下的质量投资和检验策略，研究了与检测有关的信息对双方均衡策略和利润的影响，并评估了均衡状态下对有缺陷部件进行惩罚的合理性。Xie Gang等[4]研究了全球供应链中基于订单的供应链双方在不确定需求情况下的质量投入和价格决策问题。朱立龙等[5]研究了实际的两级供应链中的质量协调问题，建立了供应链双方的期望收益函数模型，制造商对其生产过程投资水平进行决策并确定其产品质量预防水平，采购商进行质量评价决策并确定其产品质量检验水平。

供应链双方合作情形下质量协调研究主要是围绕基于产品质量的供应链契约设计[8-11]。在该种情形下，供应链双方将通过谈判的形式来实现双赢，契约设计的核心问题是供应链整体利润的合理分配。如：Reyniers[8]建立了供应链双方关于供应链质量控制的矩阵博弈模型，探讨了双方在Nash讨价还价模型下各自质量策略的选取。Yao Dongqing和Zhang Nanyun[9]从总体拥有成本(TCO)的角度运用两阶段领导-跟随博弈分析了供应链上采购商和供应商的质量成本共享契约决策。胡军等[10]研究了各种不同契约类型在供应链质量协调中的有效性。

综上所述，与现有的供应链质量协调文献相比，本文主要有两个特点：一是考虑到质量形成的长期性和动态变化特点，本文试图引入微分博弈的方法从动态角度对典型两级供应链上的质量协调机制进行研究；二是为了系统分析各种供应链质量协调机制的优劣，本文将供应链双方的质量管理行为区分为“质量控制”和“质量改进”，根据供应链双方在不同质量管理行为上的合作程度，本文将对供应链双方在非合作、部分合作和完全合作等四种不同质量管理博弈情形下的质量管理策略进行分析，从而探讨如何建立一种最优的供应链质量协调机制，以实现供应链整体效率的提升。

2 基本假设和模型的构建

本文研究的对象是以制造商作为核心企业的两级供应链。其中，制造商(m)控制产品研发、加工及装配质量；供应商(n)控制着零部件质量。为了确保最终产品的质量，核心企业(制造商)应站在全局的系统的角度对其合作企业(供应商)进行质量管理的协调。

由于质量管理活动可划为两个类型。一类是维持现有的质量，控制系统的偶发性缺陷，其方法是“质量控制”。另一类是改进目前的质量，其方法是主动采取措施，使质量在原有的基础上有突破性的提高，即“质量改进”。本文所研究的供应链上成员企业的质量管理行为将包括这两种类型的工作。这里，用A表示成员企业在质量控制上的努力，B表示成员企业在质量改进上的努力。(Am,Bm)、(An,Bn)分别表示m、n在两种工作上所花费努力的向量。鉴于努力成本的凸性特征，m和n在不同工作上的努力成本可用下面的凸函数表示：

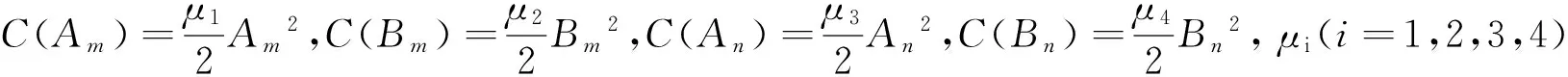
在相关研究并结合实际观察的基础上，特做出如下假设：

(1)由于产品质量是一个动态变化的过程，而产品质量的提升是由供应链上成员企业在质量改进上的努力程度来决定，于是可用式(1)所示微分方程表示产品质量的变化过程：

(1)

其中：Q(t)表示t时刻产品质量，且初始质量Q(0)=Q0；α、β分别表示m和n各自的质量改进努力对产品质量提升的影响系数；γ是质量水平的退化率。该假设条件是受文献[12]中产品声誉变化模型的启发而得到(因为质量是声誉的组成部分，它们的变化规律类似)。

(2)质量控制的目的在于监视过程，使之处于受控状态，并排除质量环中所有阶段导致不满意的原因以取得经济效益。质量改进的目的在于突破原来的质量水平，达到新的质量水平，进而通过影响客户对产品的需求来获得收益。

根据一般性假设，我们认为m和n通过各自质量控制工作所取得的收益函数是与其各自努力程度线性相关的。另外，借鉴张雄会等[13]的研究假设：因产品质量改进而产生的收益函数是与产品质量水平成正比的。

于是，可用式(2)表示m和n在产品质量管理上共同工作所产生的总收益函数：

W(Am(t),An(t),Q(t))=εAm(t)+ηAn(t)+δQ(t)

(2)

其中，ε、η和δ均为常数。ε、η分别代表m和n各自的质量控制努力对收益函数的影响程度；δ为产品质量水平对收益函数的影响系数。

(3)假设m和n联合质量管理产生的收益函数只在m和n之间分配，由于m为供应链上的核心企业，它将确定n获得收益的份额π，π∈(0，1)为常数是预先设定的，同时m将获得剩下的1-π份额。

(4)假设制造商m和供应商n有着相同且为正值的贴现率ρ，双方的目标都是在无限时区内寻求使自身利润最大化的最优质量管理策略。

基于上述假设，参考微分博弈中目标函数设置方法，得到m和n的目标函数分别为

(3)

(4)

3 模型的求解

3.1 Nash非合作质量管理博弈情形

当制造商(m)和供应商(n)进行Nash非合作质量管理博弈时，双方会同时、独立地决定各自在质量控制和质量改进工作上的努力，以最大化自身的利润。那么博弈双方的最优质量管理策略组合即为静态反馈NASH均衡。(为书写方便，后文将省略t)

定理1：在Nash非合作质量管理博弈情形下，m和n的静态反馈Nash均衡策略分别为：

(5)

(6)

证明：运用静态反馈Nash均衡的充分条件来导出对所有的Q≥0满足HJB方程的最优值函数Vm、Vn。在非合作条件下m和n的HJB方程分别为：

最大化HJB 方程式的右端可得：

(7)

(8)

将式(7)、(8)代入到HJB方程式的右端得：

(9)

(10)

由式(9) 、(10) 可知, 关于Q的线性最优值函数是HJB 方程的解。

于是，令Vm(Q)=a1Q+a2，Vn(Q)=b1Q+b2；

a1、a2、b1、b2均为常数。把它们代入到式(9)、(10)中得：

(11)

(12)

由式(11)、(12)可以得到最优值函数系数：

将系数a1、a2、b1、b2代入Vm(Q)、Vn(Q)中，得到m和n的最优值函数分别为：

(13)

(14)

进而可算出整个供应链系统的最优值函数为:

(15)

接着，将式(13)、(14)对Q的导数代入式(7)、(8)，从而得到式(5)、(6)。证毕。

3.2 制造商弱激励政策下的Stackelberg博弈情形

该种情况下，制造商仅对供应商的质量控制工作提供激励，即对供应商的质量控制努力成本进行补贴。这也是现实中比较常见的一种情况：制造商比较重视供应商所提供零部件质量的稳定性。此时，m作为领导者而n作为跟随者，双方就会进行序贯非合作博弈。m首先确定最优的两种质量管理工作努力Am、Bm以及对n质量控制努力An的补贴率h。n作为博弈跟随者在看到m的决策后再决定自己在各项工作上的努力程度，所以双方的最优策略为静态反馈Stackelberg均衡策略。

定理2：在制造商m仅对供应商n的质量控制工作提供激励的Stackelberg博弈情形下，m和n的静态反馈Stackelberg均衡策略分别为：

(16)

(17)

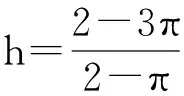
(18)

证明：该种情况m和n的博弈构成Stackelberg博弈，可运用逆向归纳法。于是问题转化为n的单方最优控制问题，其最优值函数Vn(Q)必须满足HJB方程：

(19)

使式(19)最大化的一阶条件为：

(20)

m考虑到n将根据给定的决策Am和Bm采取自身的最优策略，因此应根据n的理性反应来确定自己的最优策略，以满足自身利润最大化的目标。此时m的HJB方程为：

(21)

式(20)代入式(21)可得：

ρVm(Q)=

(22)

使式(22)最大化的关于Am、Bm和h的一阶条件分别为：

(23)

(24)

式(20)、(23)、(24)代入式(19)和(22)整理得：

(25)

(26)

显然，关于Q线性最优值函数满足式(25)和(26)。于是，令Vm(Q)=c1Q+c2，Vn(Q)=d1Q+d2；c1、c2、d1、d2均为常数。把它们及其对Q的导数代入式(25)、(26)，计算可得到最优值函数系数：

将系数c1、c2、d1、d2代入到Vm(Q)、Vn(Q)中，得到m和n的最优值函数分别为：

(27)

(28)

进而可算出整个供应链系统的最优值函数为：

(29)

接着，将式(27)、(28)对Q的导数代入式(20)、(23)，结合式(24)，从而得到式(16)、(17)和(18)。证毕。

3.3 制造商强激励政策下的Stackelberg博弈情形

该种情况下，制造商对供应商的质量控制和质量改进两种工作都提供激励，即对供应商的质量控制和质量改进努力成本都进行补贴。这是现实中比较常见的另外一种情况：制造商重视供应商所提供零部件质量的稳定性的同时，也非常关注供应商在质量改进工作上的表现。此时， m作为领导者而n作为跟随者，双方就会进行序贯非合作博弈。m首先确定最优的两种质量管理工作努力Am、Bm以及对n的质量控制努力An和质量改进努力Bn的补贴率(分别用h和s表示)。n作为博弈跟随者在看到m的决策后再决定自己在各项工作上的努力程度，所以双方的最优策略也为静态反馈Stackelberg均衡策略。

定理3：在制造商m对供应商n的质量控制和质量改进工作都提供激励的Stackelberg博弈情形下，m和n的静态反馈Stackelberg均衡策略分别为：

(30)

(31)

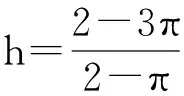
(32)

(33)

证明：同样运用逆向归纳法，证明过程类似定理2的证明过程，篇幅所限，此处省略过程，仅列出m、n以及整个供应链系统的最优值函数：

(34)

(35)

(36)

3.4 合作质量管理博弈情形

当制造商和供应商都能站在整体的角度进行质量管理工作时，双方将进行合作质量管理博弈。本部分将探讨该种理想情形。

(1)合作质量管理博弈情形下的求解

定理4：在合作质量管理博弈情形下，m和n的静态反馈Nash均衡策略分别为：

(37)

(38)

证明：在m和n进行合作质量管理博弈情形下，双方能够以供应链系统利润最优为首要原则共同地来确定各项工作努力的值。证明过程类似定理1的证明过程，篇幅所限，此处省略过程，仅列出整个供应链系统的最优值函数：

(39)

(2)合作质量管理博弈情形下的合作利润分配

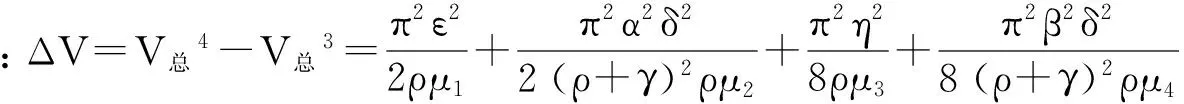
s.t.ΔVm+ΔVn=ΔV

(40)

将条件ΔVm+ΔVn=ΔV代入式(40)后，令∂U/ΔVm=0和∂U/ΔVn=0，即可求出m和n分配后的最优利润。这样就可以有效地激发合作企业参与协同质量管理的积极性。

4 比较分析

(1) 不同博弈情形下制造商和供应商的质量管理行为比较

由式(5)、(16)、(30)、(37)可知：在三种非合作质量管理博弈的情形下，制造商在两种质量管理工作上的努力程度是一样的；而在合作质量管理博弈情形下，制造商在两种质量管理工作上的努力程度要高于在非合作质量管理博弈情形下的对应值。该结论反映了制造商作为供应链上的核心企业，在缺少外界因素激励的情况下，其在两种质量工作上的努力程度是不会因不同的博弈情形而改变；但是，在合作质量管理博弈情形下，由于制造商和供应商作为一个整体，他们之间的质量管理行为存在着互补性。

(2)不同博弈情形下制造商、供应商以及整条供应链系统最优利润的比较

Vm(Q0)、Vn(Q0)是m和n在Q0(Q0≥0)的最优值函数，是无限时区上的总利润。

5 算例分析

制造商和供应商在各种不同质量管理博弈情形下，其最优质量管理工作上的努力和利润依赖模型中参数的选择。为了获得仿真数据，作者调查了一家电风扇制造商的供应链，根据调查结果，假定取ρ=0.1，ε=0.3，η=0.2，δ=0.6，μ1=0.1，μ2=0.2，μ3=0.1，μ4=0.2，α=0.4，β=0.3，γ=1，Q0=0.50，π=1/3，则在各种不同博弈情形下的制造商、供应商以及整条供应链系统的利润，其随时间变化的曲线如图1、2、3所示。

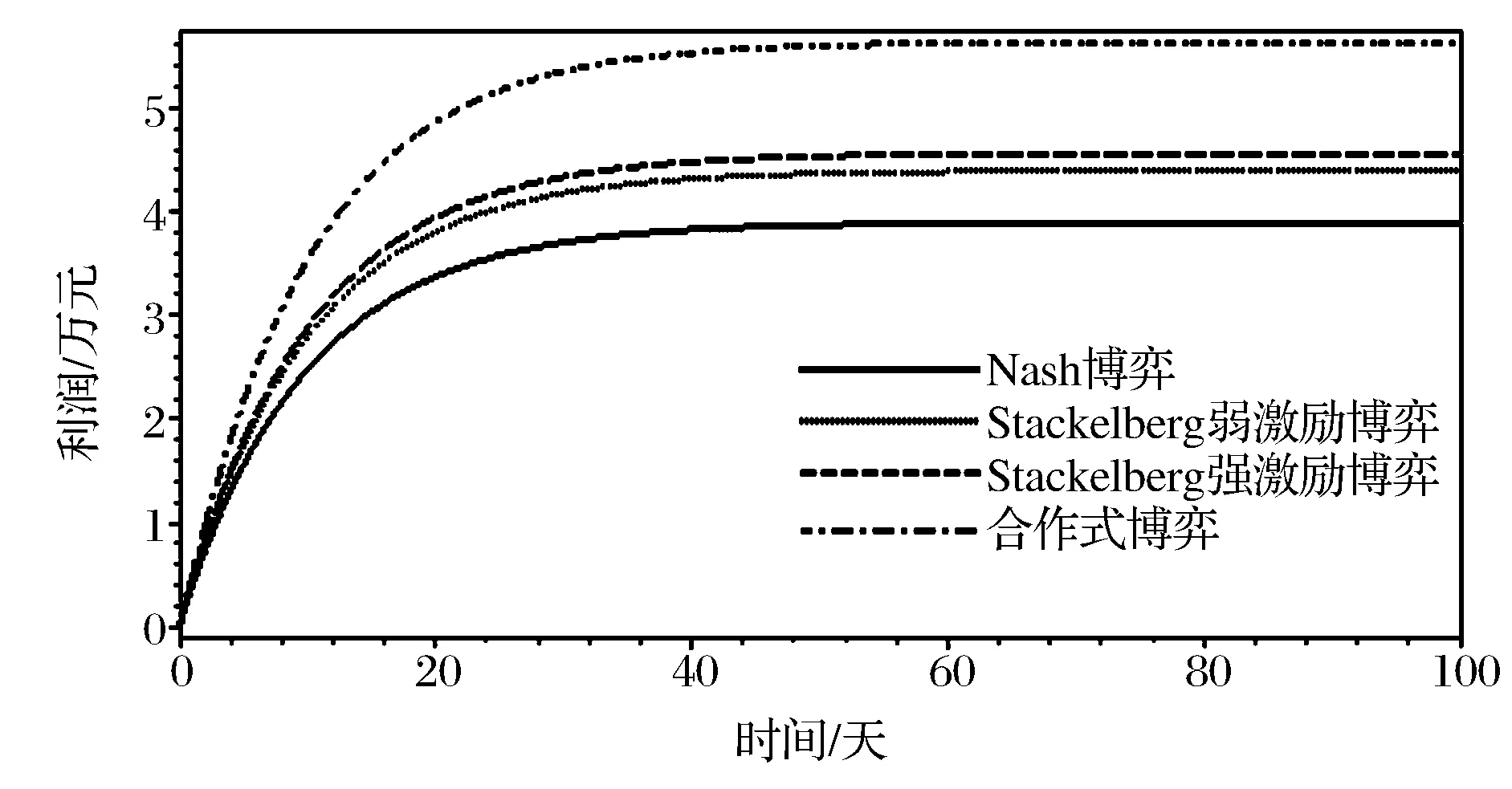
图1 制造商的利润在四种不同博弈情形下的比较

图2 供应商的利润在四种不同博弈情形下的比较

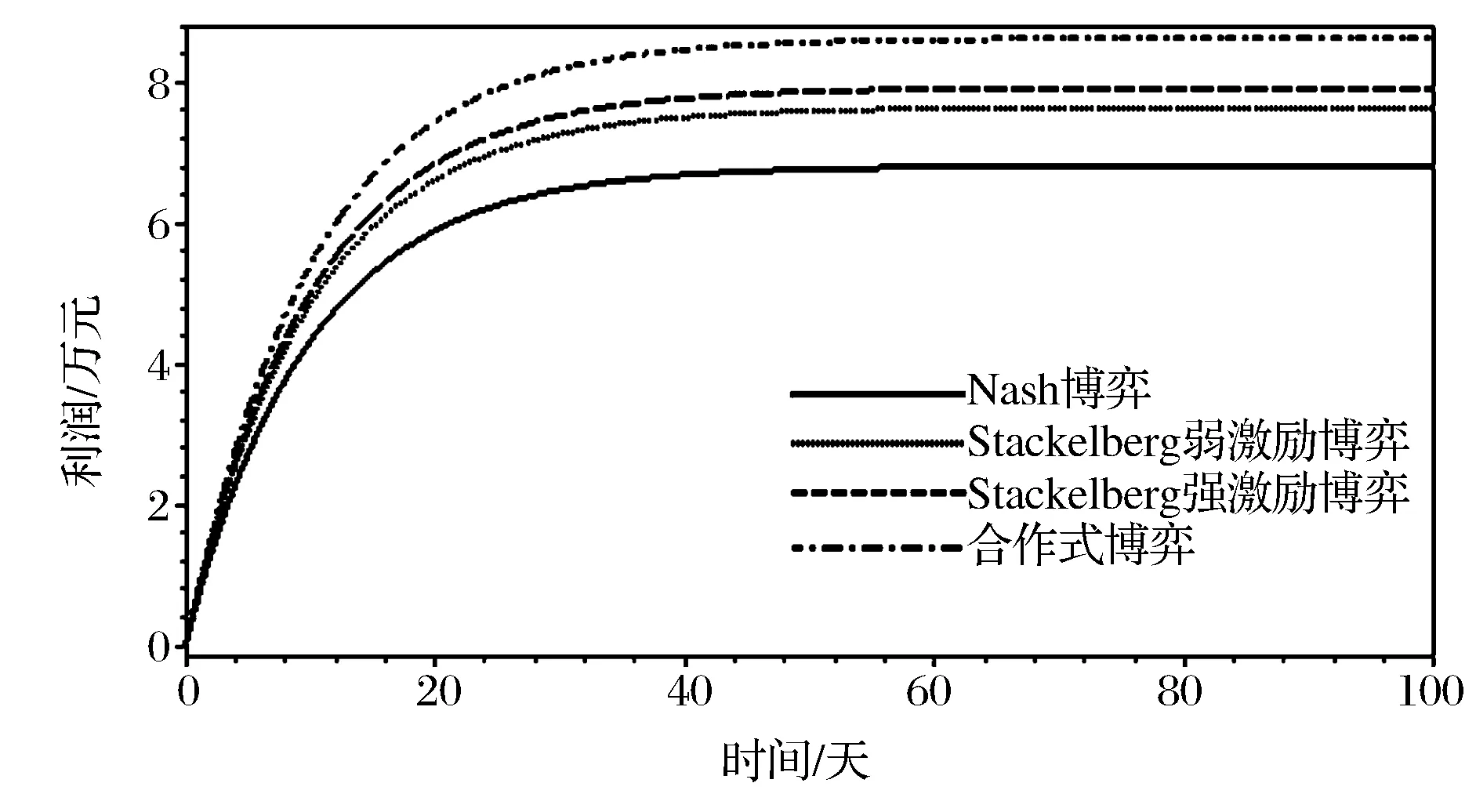
图3 整条供应链系统的利润在四种不同博弈下的比较

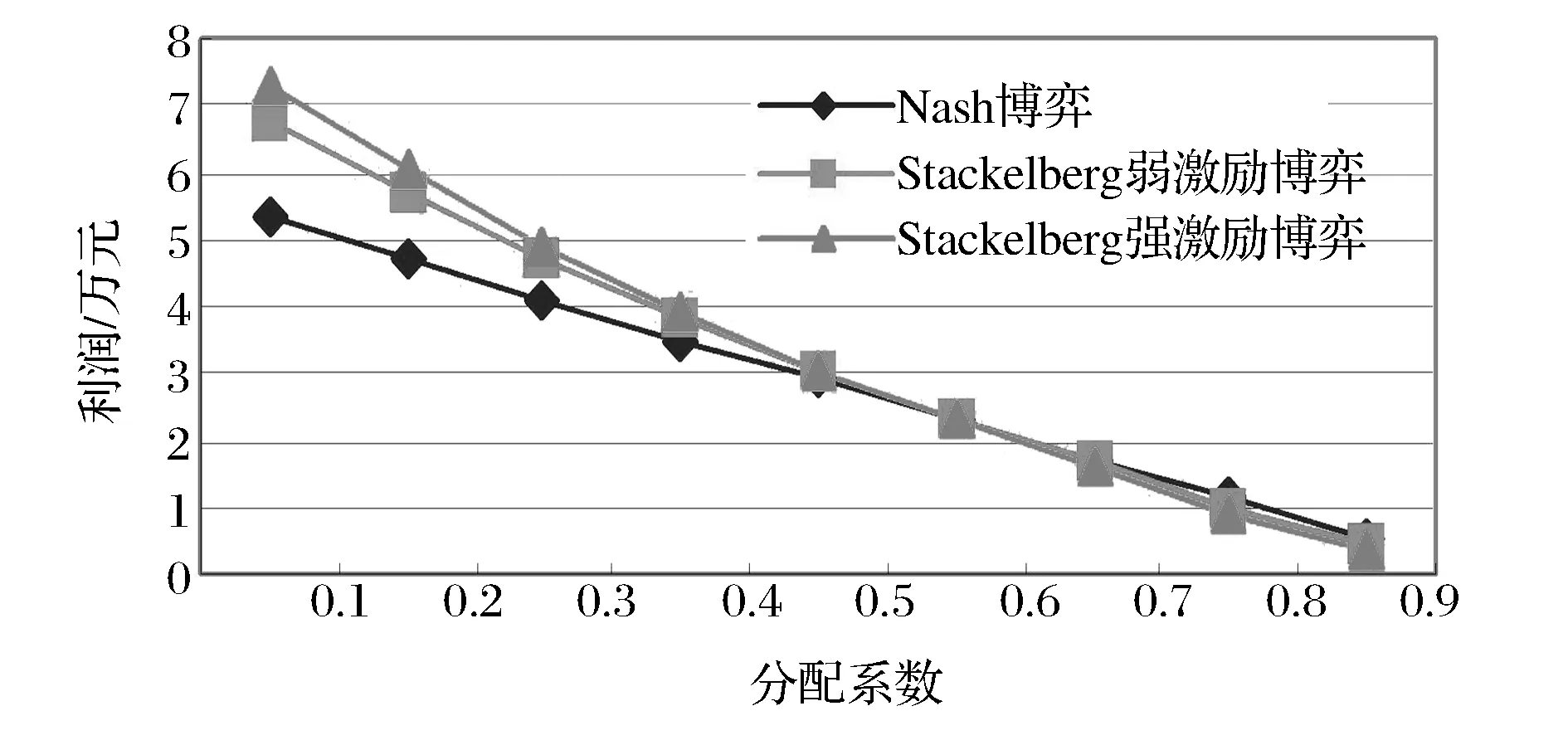
图4 不同的π值对于制造商的利润(Jm)在几种博弈情形下的影响

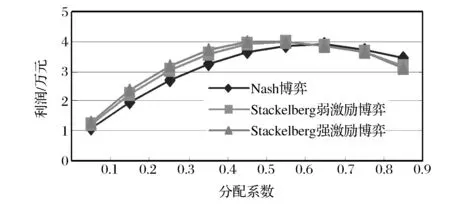
图5 不同的π值对于供应商的利润(Jn)在几种博弈情形下的影响

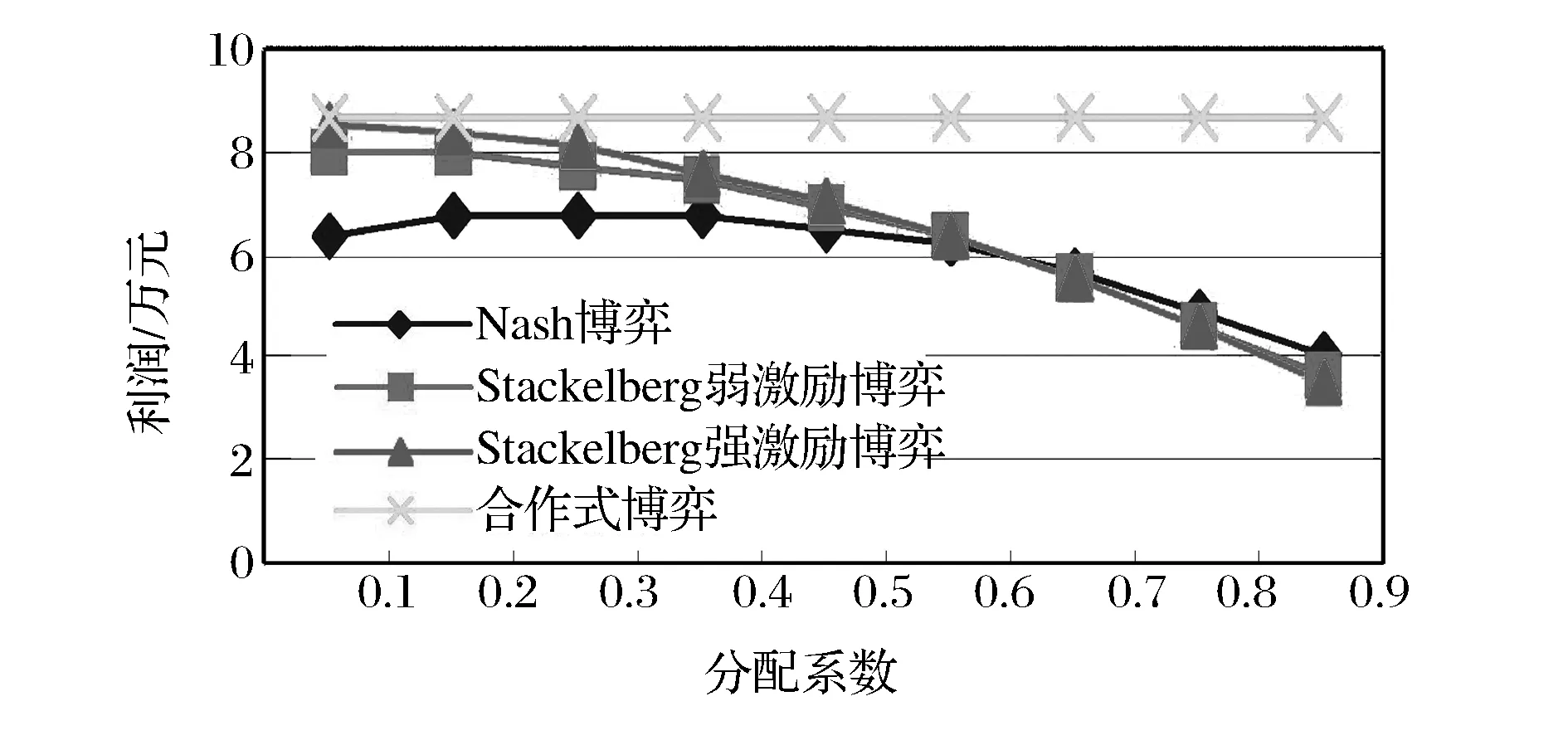
图6 不同的π值对于供应链系统的总利润(Jm+Jn)在几种博弈情形下的影响

从图1、2中可看出, 即使不对合作式博弈下的利润进行重新分配，制造商的收益从Nash非合作质量管理博弈情形，到弱激励Stackelberg博弈情形，再到强激励Stackelberg博弈情形，最后到合作质量管理博弈情形，仍将是一种帕累托改进；然而，类似的结论并不存在于供应商身上，图2反映了从Nash非合作质量管理博弈情形，到弱激励Stackelberg博弈情形，再到强激励Stackelberg博弈情形，供应商的收益是递增的，然而合作质量管理博弈情形下供应商的收益却处于Nash非合作质量管理博弈情形和弱激励Stackelberg博弈情形的收益之间。从图3中可看出, 对于制造商和供应商所组成的供应链系统的总利润来说，从Nash非合作质量管理博弈情形，到弱激励Stackelberg博弈情形，再到强激励Stackelberg博弈情形，最后到合作质量管理博弈情形，将是一种帕累托改进。所以，从图1、2、3中可以看出要想实现对制造商、供应商以及供应链系统在四种博弈情形下的帕累托改进结果，必须对供应链系统在合作质量管理博弈情形的利润增量进行合理分配。显然，以上结论与理论推导吻合。

6 结语

[1] Flynn B B， Flynn E J. Synergies between supply chain management and quality management: Emerging implications[J]. International Journal of Production Research, 2005, 43 (16): 3421-3436.

[2] 蒲国利，苏秦，刘强. 一个新的学科方向——供应链质量管理研究综述[J]. 科学学与科学技术管理, 2011, 32 (10): 70-79.

[3] Hsieh C C, Liu Yute. Quality investment and inspection policy in a supplier-manufacturer supply chain[J]. European Journal of Operational Research, 2010, 202(3): 717- 729.

[4] Xie Gang, Wang Shougang, Lai K K. Quality improvement in competing supply chains[J]. International Journal of Production Economics, 2011, 134(1): 262- 270.

[5] 朱立龙，于涛，夏同水. 两级供应链产品质量控制契约模型分析[J]. 中国管理科学, 2013, 21 (1) : 71-79.

[6] Zhu Kaijie, Zhang R Q, Tsung F. Pushing quality improvement along supply chains[J]. Management Science, 2007, 53(3): 421- 436.

[7] Xie Gang, Yue Wuyi, Wang Shouyang, et al. Quality investment and price decision in a risk-averse supply chain[J]. European Journal of Operational Research, 2011, 214(2): 403-410.

[8] Reyniers D J, Tapiero C S. The delivery and control of quality in supplier-producer contracts[J]. Management Science, 1995, 41(10): 1581-1589.

[9] Yao Dongqing, Zhang Nanyun. Contract design for supply chain quality management [J]. International Journal of Value Chain Management, 2009, 3(2): 129- 145.

[10] 胡军，张镓，芮明杰. 线性需求条件下考虑质量控制的供应链协调契约模型[J]. 系统工程理论与实践, 2013, 33 (3) : 601-609.

[11] Zu Xingxing, Kaynak H. An agency theory perspective on supply chain quality management[J]. International Journal of Operations & Production Management. 2012, 32 (4): 423 - 446.

[12] Nerlove M, Arrow K J. Optimal advertising policy under dynamic conditions[J]. Economica, 1962, 29(114):129-142.

[13] 张雄会，陈俊芳，黄培. R&D过程中供应商纵向知识溢出决策分析[J]. 工业工程与管理,2008, 13(4):29-31.

Research on Quality Coordination in Supply Chain Based on Differential Game

HONG Jiang-tao1,2, HUANG Pei2

(1.International Business School, Shanghai University of International Business and Economics,Shanghai 201620, China;2.School ofManagement, Fudan University, Shanghai 200433, China)

With the two-echelon supply chain consisting of a single manufacturer and a single supplier as its research object, the manufacturer and the supplier’s optimal quality management strategy, revenue and the total revenue of the entire supply chain in four different game situations are anylyzed. The results showed that when the income distribution between the manufacturer and the supplier met certain conditions, it was a Pareto improvement for the manufacturer, the supplier and the whole supply chain system from quality management Nash non-cooperative game situation, to weak incentive Stackelberg game situation, to the strong incentive Stackelberg game situation, and finally to the cooperation quality management game situation. Therefore, the cooperation quality management game situation was the ideal situation during the process of supply chain quality management. In order to promote the realization of the situation effectively, Nash bargaining model was applied to analyze the allocation of the remaining profits in the supply chain system between the parties. Finally, based on the simulation data got from the survey on the supply chain of an electric fan manufacturer, a numerical example was given to verify the results of the theoretical derivation.

supply chain; quality control; quality improvement; differential game; encourage

1003-207(2016)02-0100-08

10.16381/j.cnki.issn1003-207x.2016.02.013

2013-04-09；

2013-09-21

国家自然科学基金资助项目(70672071)；教育部人文社会科学研究项目(10YJC630076)

简介： 洪江涛(1980-)，男(汉族)，安徽东至人，上海对外经贸大学国际经贸学院博士，副教授，研究方向：供应链管理，E-mail:hongjiangtao2006@126.com.

F224.1

A