活用圆锥曲线定义妙解题

王晖

求三角形周长

例1 双曲线[x2a2-y2b2]= 1 （a > 0， b > 0），过焦点F1的弦AB的长为m，另一焦点为F2，则△ABF2的周长为________.

解析 如图所示，因为A，B是双曲线上的两点，

则|AF2|-|AF1|=2a.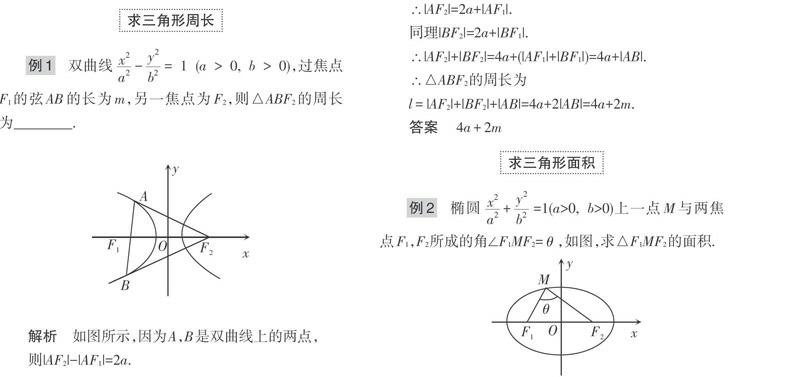

∴|AF2|=2a+|AF1|.

同理|BF2|=2a+|BF1|.

∴|AF2|+|BF2|=4a+（|AF1|+|BF1|）=4a+|AB|.

∴△ABF2的周长为

[l=]|AF2|+|BF2|+|AB|=4a+2|AB|=4a+2m.

答案 [4a+2m]

求三角形面积

例2 椭圆[x2a2+y2b2]=1（a>0， b>0）上一点M与两焦点F1，F2所成的角∠F1MF2=[θ]，如图，求△F1MF2的面积.

解析 根据椭圆定义有，|MF1|+|MF2|=2a.

将上式两边平方得，

|MF1|2+|MF2|2+2|MF1|·|MF2|=（2a）2.

根据余弦定理有，

|MF1|2+|MF2|2-2|MF1|·|MF2|cos[θ]=（2c）2.

以上两式相减得，2|MF1|·|MF2|（1+cos[θ]）=4b2.

∴|MF1|·|MF2|=[2b21+cosθ].

∴[SΔF1MF2]=[12]|MF1|·|MF2|sin[θ]

=[12]·[2b21+cosθ·sinθ=]b2·[sinθ1+cosθ]

= b2tan[θ2].

求距离

例3 如果双曲线[x264-y236]= 1上一点P到它的右焦点的距离为8，那么P到它的左准线的距离是______.

解析 设双曲线的左、右焦点分别是F1，F2，P到左准线的距离为d.

则由双曲线方程可知，a=8， b=6. 这样就不难判定P点在双曲线的右支上.

由双曲线的第一定义有，|PF1|-|PF2|=2a=16，

∴|PF1|=16+|PF2|=16+8=24.

由双曲线的第二定义有，[|PF1|d]= e.

∴d =[|PF1|e]=[2454]=[965].

答案 [965]

有关轨迹问题

例4 如图，已知圆的方程为x2+y2=4，点A，B的坐标分别为（-1， 0），（1， 0），动抛物线过A，B两点，且以圆的切线为准线，求抛物线的焦点F的轨迹.

解析 设抛物线焦点F （x， y），过A，O，B作圆的切线的垂线，垂足分别为C，P，D，

则由抛物线的定义得，|FA|=|AC|，|FB|=|BD|.

从而|FA|+|FB|=|AC|+|BD|=2|OP|=2R=4.

由椭圆定义可知，点F的轨迹是以A，B为焦点的椭圆，且a=2， c=1.

故所求焦点[F]的轨迹方程为[x24+y23]=1.

求定值

例5 已知抛物线y2=4x，如图，过焦点F的弦AB被焦点分成FA，FB两部分，求[1|FB|]+[1|FA|]的值.

解析 由题意得，p=2.

设A，B两点的横坐标分别为x1，x2，过A，B分别作准线的垂线，垂足分别为N，M.

根据定义可知，|FA|=|AM|，|FB|=|BN|.

∴[1|FB|]+[1|FA|]=[1|AM|+1|BN|]=[1x1+p2]+[1x2+p2]

=[x1+x2+px1x2+p2（x1+x2）+p24].

∵AB是过抛物线y2=4x焦点的弦，

∴x1x2 =[p24].

∴[1|FB|]+ [1|FA|]=[x1+x2+pp22+p2（x1+x2）]

=[x1+x2+pp2（x1+x2+p）]=[2p]= 1.

求最值

例6 给定点A （-2， 2），已知点B是椭圆[x225+y216]=1上的动点，F为椭圆的左焦点，求[|AB|+53|BF|]的最小值，并求点B的坐标.

解析 如图，椭圆的左准线l：x=[-253]. 作BN⊥l，垂足为N.

由椭圆第二定义可知，[|BF||BN|]=e=[35].

则[53]|BF|=|BN|.

∴|AB|+[53]|BF|=|AB|+|BN|≥|AN|，当且仅当A，B，N三点共线时，|AB|+[53]|BF|取得最小值|AN|，易得，|AN|=[253]-2=[193].

此时B（x0， 2），且x0<0. 将点B的坐标代入椭圆方程得，x0=[-532].

所以当点B的坐标为（[-532]， 2）时，|AB|+[53]|BF|取得最小值[193].

求离心率

例7 如图，已知F1，F2为椭圆C1的左、右焦点，抛物线C2以F1为顶点、F2为焦点. 设P是椭圆与抛物线的一个交点，椭圆C1的离心率为e，且|PF1|=e|PF2|，求离心率e的值.

解析 设抛物线的准线为l，易得l：x=-3c，其中F1（-c， 0），F2（c， 0）. 作PN⊥l，垂足为N. 点P在抛物线上，F2为抛物线的焦点，由抛物线定义可知，|PF2|=|PN|.

又[|PF1||PF2|]= e，所以[|PF1||PN|]= e.

又点P在椭圆C1上，由椭圆第二定义可知，|PN|为点P到左准线的距离，即椭圆的左准线与抛物线的准线重合，椭圆的左准线方程为x=–[a2c]，

则–[a2c]= -3c，所以e =[ca]=[33].

所以椭圆C1的离心率e =[33].

求轨迹方程

例8 已知圆O的方程为x2+y2=100，点A的坐标为（-6， 0），M为圆O上任意一点，AM的垂直平分线交OM于点P，求P的轨迹方程.

解析 如图，设P点的坐标是 （x， y），连结AP.

∵P在AM的垂直平分线上，

∴|AP|=|PM|.

∵|OP|+|PM|=|OM|=10，

∴|AP|+|PO|=10.

根据椭圆的定义可知，P点的轨迹是以A，O为焦点的椭圆.

∵A（-6， 0），O（0， 0），

∴椭圆中心为（-3， 0）.

由2a=10得，a=5.

又c=3，所以b2=a2-c2=16.

故P点的轨迹方程是[（x+3）225+y216]= 1.

正确地运用圆锥曲线定义求解数学问题，给人一种返璞归真之感. “回到定义上去”这一解题策略要求我们，要懂得数学概念发生作用的那些问题和数学概念在研究这些问题中的特殊用处. 利用此法解题，不仅可以优化解题过程，并且对培养思维的敏捷性，促进解题能力的提高，都是非常有益的.