梁弯曲正应力公式适用条件探讨
韩芳,磨季云,李明方
(1. 武汉科技大学 理学院,湖北 武汉 430081;2. 冶金工业过程系统科学湖北省重点实验室,湖北 武汉 430081)
梁弯曲正应力公式适用条件探讨
韩芳1,2,磨季云1,李明方1
(1. 武汉科技大学 理学院,湖北 武汉 430081;2. 冶金工业过程系统科学湖北省重点实验室,湖北 武汉 430081)
材料力学和弹性力学作为工科类专业的一门基础课,公式较为复杂.针对材料力学和弹性力学中对梁弯曲正应力推导方式的不同,基于弹性力学有限元理论,采用有限元数值仿真软件模拟不同跨高比条件下梁弯曲正应力的数值解,并与材料力学近似解进行对比和误差分析,得到深梁和浅梁弯曲正应力公式的适用条件,为学生更形象直观地理解知识点提供新的视角.
弹性力学;材料力学;弯曲正应力;力学课程
力学是理工科学生的基础课,目前在力学课程教学中,材料力学在求解横力弯曲梁构件的弯曲正应力时沿用了纯弯曲时的计算公式,即采用了平面假定和各纵向纤维无挤压的假定,得出的解是近似的[1];弹性力学采用半逆解法对均布荷载作用下的梁构件进行了受力分析,结果形式复杂但精度较高[2-3].一些研究人员对深梁和浅梁的应力分析也展开了讨论[4-6],授课过程中学生也会对2门课的同一个问题的不同解法产生疑虑.为了更直观地表现应力解随跨高比的变化规律,本文基于弹性力学有限元理论,采用有限元分析软件ANSYS对不同跨高比条件下的梁进行受力分析[7-8],得到其弯曲正应力随跨高比变化的分布规律,为学生更形象直观地理解知识点提供新的视角.
1 材料力学解
材料力学在求解横力弯曲梁构件的弯曲正应力时沿用了纯弯曲时的计算公式,即采用了平面假定和各纵向纤维无挤压的假定,通过应力应变之间的物理关系,找出正应力在横截面上的分布规律,再利用静力平衡条件得到弯曲正应力与横截面上弯矩间的关系,得到近似解[9-10]

其中:M为横截面上的弯矩;Iz为截面的形心主惯性矩;y为横截面上正应力计算点处到中性轴的距离.
2 弹性力学解
取单位宽带的矩形截面简支梁(高度为h,长度为2l,不计体力)分析在均布荷载q作用下简支梁的弯曲正应力,经过假设应力分量函数形式,推求应力函数,由相容方程求解应力函数,由应力函数求解应力分量,代入边界条件等步骤后,得到弯曲正应力解析表达式


3 有限元建模与分析
图1 跨高比为2时的模型(深梁)
图2 跨高比为10时的模型(浅梁)
取跨中节点的应力和位移为考察点,得到不同跨高比条件下的应力解和位移解见表1、表2,应力误差和位移误差见图3、图4.

表1 不同跨高比条件下材料力学解与有限元解应力对比分析

表2 不同跨高比条件下材料力学解与有限元解位移对比分析
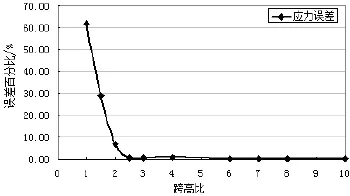
图3 不同跨高比条件下的应力误差

图4 不同跨高比条件下的位移误差
从图3可以看出,随着跨高比的增大,材料力学公式解和弹性力学有限元解之间的误差逐步在减小.当跨高比在1~2.5之间,曲线变化陡降,误差较大;当跨高比大于2.5时,其应力误差已小于工程上所允许的最大误差值5%,在可接受的范围内,此后误差保持在一个相当低的水平,这表明跨高比对节点应力的影响较小,可以忽略不计.换言之,采用材料力学应力公式求解梁的弯曲正应力是符合工程精度要求的.
从图4可以看出,随着跨高比的增大,位移误差逐步在减小.当跨高比在1~5之间,曲线变化陡降,误差较大;当跨高比大于5时,其位移误差已在工程上所允许的范围内.
通过对比材料力学解析解和弹性力学数值解的区别,可以为学生这样解释:深梁在均布荷载作用下,除受弯矩作用产生变形和应力以外,还因剪力作用梁上任意两个相邻截面之间发生了相对错动,产生附加挠度,同时剪应力沿横截面高度的非均匀分布使得截面不再保持为平面而引起翘曲,从而影响弯曲正应力的分布,区别于材料力学中的浅梁解.数值计算表明,当跨高比不小于5时,梁中各节点的正应力公式解和有限元解之间相差不大,已在可允许的范围之内,在工程实际计算中采用材料力学公式解是可行的,但当跨高比小于5时,公式解的误差太大,必须按照弹性力学求解.
4 结论
针对材料力学和弹性力学中对于梁弯曲正应力的公式推导过程的不同,采用数值仿真技术直观显示梁弯曲正应力随梁跨高比的变化,定量得到公式的适用条件,有助于学生对知识点的理解和记忆.
[1] 李卓球.工程力学[M].武汉:武汉理工大学出版社,2009
[2] 徐芝纶.弹性力学简明教程[M].北京:高等教育出版社,2002
[3] 王润富.弹性力学简明教程学习指导[M].北京:高等教育出版社,2004
[4] 孙晔青.对横力弯曲梁的正应力和挠度计算精度的研究[J].南昌航空工业学院学报,2000,14(4):56-60
[5] 梅甫良,曾德顺.深梁的精确解[J].力学与实践,2002,24(1):58-60
[6] 徐礼华,池寅,李荣渝,等.钢纤维混凝土深梁非线性有限元分析ANSYS中的实现[J].岩土力学,2008,29(9):2577-2582
[7] 董冠文,李宗义,王泽萌,等.工程力学的教学改革研究[J].高师理科学刊,2015,35(4):93-97
[8] 胡清明,李东生,郭建华,等.有限元技术在工程力学教学中的应用探索[J].高师理科学刊,2014,34(1):104
[9] 夏桂云,曾庆元.深梁理论的研究现状与工程应用[J].力学与实践,2015,37(3):302-316
[10] 周道祥.用材料力学解的切应力求解弹性力学问题[J].力学与实践,2010,32(2):116-118
Discussion on application conditions of bending normal stress in mechanics
HAN Fang1,2,MO Ji-yun1,LI Ming-fang1
(1. School of Science,Wuhan University of Science and Technology,Wuhan 430081,China;
2. Hubei Province Key Laboratory of Systems Science in Metallurgical Process,Wuhan 430081,China)
Mechanics of materials and elasticity is an important course for engineering major students as its abstract theory and various formulas. For the different derivation process of the bending normal stress for deep beam and shallow beam in elastic mechanics and material mechanics,does research on the numerical solution for the bending normal stress of beams with different span-depth ratio based on the software and elastic finite element method theory. The simulation results are compared with the analytical solution and the application conditions of bending normal stress of deep beam and shallow beam are obtained applying a new viewpoint for understanding.
elastic mechanics;material mechanics;bending normal stress;mechanics
O34∶G642.0
A
10.3969/j.issn.1007-9831.2016.06.027
1007-9831(2016)06-0092-03
2016-05-15
冶金工业过程系统科学湖北省重点实验室基金项目(Y201519)
韩芳(1980-),女,湖北丹江口人,副教授,博士,主要从事工程力学研究.E-mail:hanfang522@163.com

