初中“几何变换”的内容与考法的剖析
周春意

摘要:随着教育教学改革的深入发展,现代数学思想也随之不断渗透,几何变换以运动变换的观点研究几何问题,体现了“形”与“数”的知识融合,把复杂性问题转化为简单性的问题而得到解决,逐渐成为中考考查热点、重点。它的数学思想已越来越引起人们的重视和关注。明确“几何变换”的内容本质特点及中考测试点,有利于提高教学与复习效率。
关键词:初中数学;“几何变换”;内容与考法
中图分类号:G633.6 文献标识码:A 文章编号:1992-7711(2016)07-0093
随着教育教学改革的深入发展,现代数学思想也随之不断渗透,几何变换以运动变换的观点研究几何问题,体现了“形”与“数”的知识融合,把复杂性问题转化为简单性的问题而得到解决,逐渐成为中考考查热点、重点,它的数学思想已越来越引起人们的重视和关注。明确“几何变换”的内容本质特点及中考测试点,有利于提高教学与复习效率。
一、内容剖析
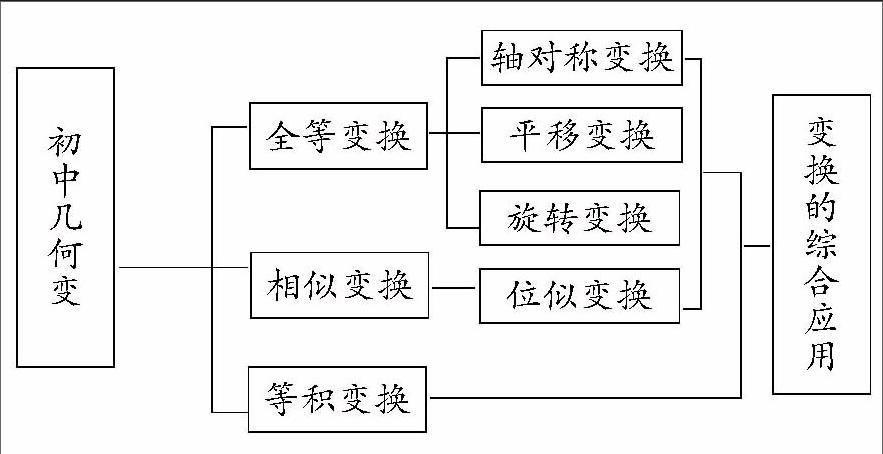
1. 知识结构
2. 知识要点
全等变换问题(轴对称、平移、旋转)全等变换:是指不改变图形形状与大小的变换。
首先要理解运用这种变换的一些基本情况:
(1)按指令语言,按规定的变换移动图形;
(2)按指令语言拼接图形;
(3)根据题目的需要设计变换(需要理解变换的条件与相应的方式与方法;需要解读好题目的直接或隐含的条件)。
相似变换问题。位似变换:是指不改变图形形状只改变图形大小的变换。
由于相似的知识不是建立在以平行线为依据的前提下,所以我们对图形的认识是建立在位似变换的基础之上的,即从位似化为相似,也就是说需要先从相似的角度认识问题.从新课标的角度讲相似问题的知识只是要求为基本认识,纯推理的问题相对困难,所以我们对这部分知识的定位是以数量计算为主要对象的。
等积变换问题。等积变换:是指不改变图形大小只改变图形形状的变换。
这是新课标在重视几何变换的前提下与实际问题相结合而形成的问题,它主要体现在以下问题中:①图形在不改变大小的情况下的移动;②图形的分割与组合;③图形的拼接。
3. 主要思想方法
轴对称你变换:轴对称是平面到自身的变换,若存在一条定直线l,使对于平面上的每一点P及其对应点P′,其连线PP′都被定直线l垂直平分,则称这种变换为轴对称变换,定直线l称为对称轴。轴对称变换有如下性质:(1)把图形变为与之全等的图形;(2)关于l对称的两点连线被l垂直平分。
证题过程中使用翻折变换,可保留原有图形的性质,且使原来分散条件相对集中,以利于问题的解决。
平移变换:平移变换是平面到自身的变换,将平面上任一点P变换到P′,使得:(1)射线PP′有给定的方向;(2)线段PP′有给定的长度,则称这种变换为平移变换。在平移变换下,图形变为与之全等的图形,直线变为与之平行的直线。
在解几何问题时,常利用平移变换使分散的条件集中在一起,具有更紧凑的位置关系或变换成更简单的基本图形。
下面是一些常用到的平移变换的特殊情形:(1)与定长、定向的线段有关的问题,常作平移;(2)与梯形、正方形有关的问题,常可利用梯形、正方形的特性作平移。
旋转变换:旋转变换是平面到它自身的变换,使原点O变换到它自身,其他任何点X变到X′,使得:(1)OX′=OX;(2)∠XOX′=θ(定角),则称这样的变换为旋转变换,O称为旋转中心 。旋转变换保持图形全等,但图形方位可能有变化。在几何解题中,旋转的作用是使原有图形的性质得以保持,但改变其位置,使能组合成新的有利论证的图形。
在运用旋转变换解几何题时,注意下面一些特殊情形:
(1)与等腰三角形有关的问题,常取顶角的顶点为旋转中心,作旋转变换;
(2)与正三角形(或正方形)有关的问题,常可利用正三角形(或正方形)的特性作旋转变换;
(3)与圆有关的问题,常取圆心为旋转中心作旋转变换。
当图形中存在(或适当添加辅助线之后存在)等线段、特别角、全等形、正多边形等情况时,常常可以试探作一个有用的旋转变换,使得这个变换带来新的全等形、相等的线段、相等的角等,从而将巳知条件相对集中,以利于问题的解决。
位似变换:位似变换是两个图形不但相似,且每组对应点所在的直线都经过同一点,那么这就是位似图形。(初中数学中考中暂不命题)
等积变换:等积变换是指在解某些几何问题时,通过几何图形的面积相等,相互间进行转换,从而使问题得到解决。
4. 重点与难点
几何变换的重点:了解图形轴对称变换、平移变换、旋转变换、相似变换的概念;会按要求作出简单平面图形经轴对称变换、平移变换、旋转变换、相似变换后所得的像;理解轴对称变换、平移变换、旋转变换的性质:均不改变原图形的形状和大小;了解图形相似变换的性质;通过对图形变换的欣赏和探索,使学生体会图形变换在现实生活的存在,激发学生的数学学习兴趣,增强审美观念,培养学生的科学探究精神。
几何变换的难点:平移变换得根据所提供的平移方向和移动的距离两个条件作图;旋转变换得根据旋转中心、旋转的方向和角度三个条件作图,“以局部带整体”的作图思想方法,进一步发展学生的空间观念;能利用轴对称、平移、旋转等方法绘制精美的图案。
二、考法剖析
几何变换以运动变换的观点研究几何问题,体现了“形”与“数”的知识融合,逐渐成为中考考查热点、重点,提高了学生运用几何变换的思想分析、解决问题的能力,它的数学思想已越来越引起人们的重视和关注。
1. 概念性问题——考查学生的基本概念
例1. (2015北京市中考题) 剪纸是我国传统的民间艺术,下列剪纸作品中,是轴对称图形的为( )
例2. (2015年哈尔滨市中考题)如图,在RtABC中,BAC=90°,将ABC绕点A顺时针旋转90°后得到AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接C。若CC′B′=32°,则B的大小是( )
A . 32° B. 64° C. 77° D. 87°
2. 开放性问题——考查学生的创造能力
例3. 已知每个网格中小正方形的边长都是1,图1中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成。
(1)填空:图1中阴影部分的面积是 (结果保留π);
(2)请你在图2中以图1为基本图案,借助轴对称、平移或旋转设计一个完整的花边图案(要求至少含有两种图形变换)。
这类开放题不同于在固定条件下研究固定结论,学生可以从日常生活、生产或学习中多角度、多层次、多侧面地思考问题,发展学生的求异思维,对于激发学生的学习兴趣,发挥学生的主体精神,考查学生的个体很有益处。
3. 应用性问题——考查学生的综合应用能力
例4. (2015年葫芦岛中考题)如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形ABnCnCn-1的面积为 。
例5. (2015年庆阳市中考题)在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
4. 探究性问题——考查学生的分析能力
例6. (2015年岳阳市中考题)已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点。
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: 。
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由。
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k。求证:PA·PB=k·AB。
这类题型主要通过学生的观察、分析、探究、猜测、推理、验证等一系列探究活动,从不同的角度和层次来分析和解决问题,体现了新课程标准下要求教师形成开放性、创新性的教学方式,体现了主体性、反思性和合作性等教学思想,要求学生学会“问题——探究——发现——推广”。因此,此题注重研究探究性问题,做到合情推理和演绎推理相结合,较好地考查学生的分析能力。

