巧解一道二元最值问题

广东省佛山市罗定邦中学(528300) 龙宇 孙琼

巧解一道二元最值问题

广东省佛山市罗定邦中学(528300) 龙宇 孙琼

本文应用待定系数法、整体法及该二元问题的几何意义来求解该问题.

待定系数法整体法数形结合

在很多期刊上面都出现了如下这道例题:设实数x,y满足4x2−5xy+4y2=5,求x2+y2的取值范围.该题的解法很多,但大多应用换元的方法求解.如文[1]、[2]、[3].本文转换思路,尝试应用如下方法,求解该题.

1.待定系数法

解对于条件,设

同理,我们也可以得到x2+y2的最小值.不过要将题目变形为:

2.整体法

由方法1可知,在原题干下可得

一般的证明思路都是先证一边,再证另一边.其实该结论也可以同时证明.该不等式等价于

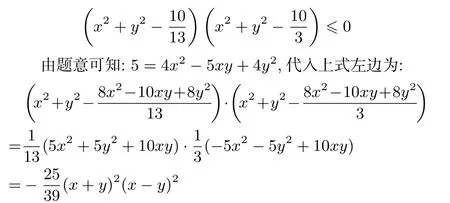
上式显然≤0,原命题成立.

显然方法2属于验证性证明,方法1属于获得性证明.但在多数情形下,题目的答案是未知的,所以方法1的实用性更强一些.

3.数形结合1

由文[4]可知,定理1:当Ax2+Bxy+Cy2=D,D≠0有无数个解时,当B2−4AC＜0时,Ax2+Bxy+Cy2= D,D≠0表示的曲线是椭圆,当B2−4AC＞0,Ax2+Bxy+Cy2=D,D≠0表示的曲线是双曲线.

对于4x2−5xy+4y2=5,A=4,B=−5,C=4,满足B2−4AC＜0.所以该式对应的图像是一个椭圆.但该椭圆的对称轴并不在坐标轴上.现做一个线性代换,将其对称轴旋转到坐标轴上.

令x=u+v,y=u−v.原题干转变为3u2+13v2=5,如图1所示,令u为横轴,v为纵轴.

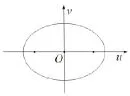
图1

对于x2+y2,转换为2u2+2v2.那么该问题就转换为如下的一道几何题目,已知椭圆C:3u2+13v2=5,求椭圆C上一点P,使点P到原点距离的平方的2倍为最大或最小,即2u2+2v2的最值.

根据椭圆的性质,该最值一定在椭圆的四个顶点处取得,易知

4.数形结合2

将式4x2−5xy+4y2=5,变形为联系余弦定理,x,y可表示为某一个三角形的两条边.且该三角形的一条边为且该边所对角θ的余弦值为弊端:三角形要求各边长必须＞0,而原题干中x,y为实数.所以该方法只能求得当x,y＞0或x,y＜0(若x,y＜0,则有−x.−y＞0,再代入上式.)时,x2+y2的范围.所以不妨设x＞0,y＞0.

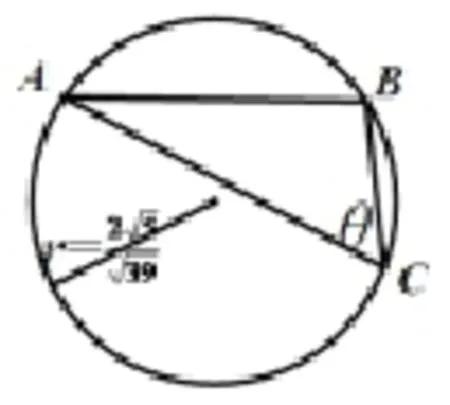
图2

[1]徐元根.二次方程约束条件下的一类取值范围问题[J].数学通报,2007,9.

[2]姜坤崇.一类求取值范围问题的解法[J].数学通报,2006,4.

[3]厐景生.用三角换元巧解二元齐次式的最值[J].中学生数学,2007,5上.

[4]翁锦春,陈文灶.圆锥曲线与二元二次方程[J].福建师大福清分校学报,1993,3.