对一道华附复数题的深入探究和变式分析

广东省汕头市聿怀实验学校(515000) 蔡昇

对一道华附复数题的深入探究和变式分析

广东省汕头市聿怀实验学校(515000) 蔡昇

题目展示若对一切θ∈R,复数z=(a+cosθ)+(2a−sinθ)i的模不超过2,则实数a的取值范围为___.(2011届华附、省实、广雅三校广州一模后联合适应性考试)

1.正常思维—代数求解从正常角度出发,上述题目是复数和不等式结合问题,用代数的方法求解是可以求出来的.

整理得到:0≤(a+cosθ)2+(2a−sinθ)2≤4,

也就是:−1≤5a2+2acosθ+4asinθ≤3,

根据三角函数化简的规律,得

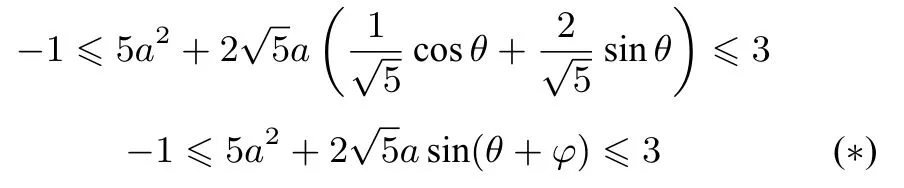
其中φ为定值,因为其不影响后续讨论,故不用求出.

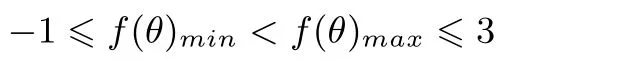
由于自变量取值范围为R时,Asinx函数值的范围由A决定.所以,上述不等式转化成下述表示:

解后反思本题在3个方面设下了困难:(1)在化简的过程中,不能想到采用辅助角,就无法继续完成.(2)化简后无法把三角函数看做整体,从而考虑最大值、最小值问题.(3)抓住了学生的惯性思维,让学生在以为这类题很熟悉的情况下,对a的取值讨论不充分,从而漏掉了解,导致答案出错.

2.灵活变通—数形结合题目解题操作困难,就需要我们去发掘较为简便灵活的解法,本题恰有这样的特点.本题可以通过转化成为:与圆上一点距离值大小问题相关的问题.

笔者从复数z=x+yi得到启发,通过对比z=x+yi与z=(a+cosθ)+(2a−sinθ)i的形式,知道可以尝试设x=a+cosθ,y=2a−sinθ.整理后,得x−a=cosθ,y−2a=sinθ.由于对此题的方向变为将其转化为与圆的方程相关的问题,根据cos2θ+sin2θ=1,有(x−a)2+(y−2a)2=1,这个方程的图像如下图1,也就是圆心在(a,2a),半径为1的圆O,并且可知圆心在直线y=2x上运动.

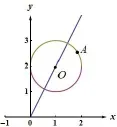
图1

整理后得

解后反思本题新解的好处是通过数形结合的方法,将原本复杂的代数讨论变成距离长度的讨论.而且由于线段长度是正值,减少了部分讨论.并且新解法和圆上移动点相联系,并且涉及到圆心在定直线运动的特点,对于进一步思考圆上动点问题有抛砖引玉之效.

3.思维拓展—变式分析

出于对第二种解法的思考,考虑下述变式:(1)若对一切θ∈R,复数z=(a+cosθ)+(2a−sinθ)i的模不超过3,则实数的取值范围为____.

变式思考:改变解题过程中的呈现的复数的模,从而改变题目.

(2)若对一切θ∈R,复数z=(a+cosθ)+(a−sinθ)i的模不超过2,则实数的取值范围为____.

变式思考:改变解题过程中的圆心所在定直线,从而改变题目.

(3)若对一切θ∈R,复数z=(a+cosθ)+(2a− sinθ)i的模不小于2,则实数的取值范围为____.

变式思考:改变解题过程中的对于模的大小限定范围,从而改变题目.

(4)若对一切θ∈R,复数z=(a+cosθ)+(a−2sinθ)i的模不超过3,则实数的取值范围为___.

变式思考:改变解题过程中的圆锥曲线,将圆变成椭圆,并让学生自行探究椭圆心在定直线上的椭圆,何时距离原点最远,从而改变题目.上述变式只是笔者稍作尝试,读者之后也可以继续思考.