数独的数学模型与LINGO求解程序
柯春梅
(厦门海洋职业技术学院基础部,福建厦门 361101)
数独的数学模型与LINGO求解程序
柯春梅
(厦门海洋职业技术学院基础部,福建厦门 361101)
本文首先从标准数独的条件与规则出发,引入三元0-1变量,建立标准数独的0-1整数规划模型,根据模型设计LINGO求解程序,用一个数独难题进行验证,说明程序计算的准确性;然后将标准数独的LINGO求解程序推广到窗口数独、额外区域数独、奇偶数独等三种变形数独的求解;最后利用数独联盟五段段位考试训练题进行验证,运算时间不超过2秒,准确率达到100%,说明这些LINGO程序求解数独问题,速度快且结果准确可靠。
LINGO软件;标准数独;0-1整数规划;变形数独
LINGO是求解优化问题的专业软件包,它内置建模语言,提供几十个内部函数,从而能以较少的语句、较直观的方式描述大规模的优化模型,它的运算速度快,计算结果可靠[1]。
所谓标准数独,就是用9×9的方阵构成81个格子,其中9个用粗线分隔的区域称为宫,在其中的一些格子里已经填上了1到9之间的数字,还留下若干空格,要求数独参与者将这些格子填满,结果满足每一行、每一列、每个宫的9个数字都是由1到9组成,没有重复数字[2]。数独联盟将标准数独进行变形,推出多种变形数独。数独游戏全面考验做题者的观察能力和推理能力,虽然玩法简单,但数字排列方式却千变万化,所以不少教育者认为数独游戏是训练头脑的绝佳方式。国内许多学者对数独的教学意义进行讨论,用计算机进行快速求解的算法,这些算法多数以回溯法为基础,结合各种预处理提高算法的执行速度[3-7],而对通过建立数学模型、利用数学软件进行求解的算法的研究很少[8-9]。本文将标准数独的求解程序推广到窗口数独、额外区域数独和奇偶数独的求解程序,快速准确求解数独问题,同时训练LINGO软件的使用技巧。该研究实现了运用数学软件快速准确求解变形数独。
1 标准数独的数学模型与LINGO求解程序
宫的行状为3×3正方形的数独称为标准数独,图1就是一个标准数独[3]。

图1 标准数独

图2 标准数独的解
1.1 标准数独的数学模型
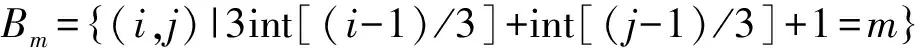
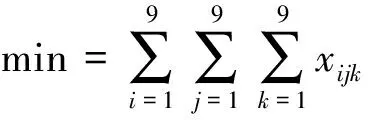
其中,(1)表示yij与决策变量的关系;(2)表示每个格子(i,j)处只能填1~9中的一个数;(3)表示每行1~9中的每个数只能填一次;(4)表示每列1~9中的每个数只能填一次;(5)表示每个区1~9中的每个数只能填一次。
1.2 标准数独的LINGO求解程序
利用LINGO编程语言,对标准数独建立的0-1整数规划模型进行程序设计,其求解程序如下:
model:
sets:
number/1..9/;line/1..9/;col/1..9/;gong/1..9/;
shudu(line,col):y,a;
link(line,col,number):x;
endsets
data:
! 键盘输入;
a=?;
enddata
min=@sum(link:x);
@for(shudu(i,j) | a(i,j) #ge# 1:x(i,j,a(i,j))=1);
@for(line(i):@for(col(j):@sum(number(k):x(i,j,k))=1));
@for(line(i):@for(number(k):@sum(col(j):x(i,j,k))=1));
@for(col(j):@for(number(k):@sum(line(i):x(i,j,k))=1));
@for(line(i):@for(col(j):y(i,j)=@sum(number(k):k*x(i,j,k))));
@for(gong(m):@for(number(k):@sum(link(i,j,k)| 3*@floor((i-1)/3)+@floor((j-1)/3)+1 #eq# m:x(i,j,k))=1));
@for(link(i,j,k):@bin(x(i,j,k)));
End
1.3 标准数独的求解
运用上述程序求解标准数独问题时,只需在键盘输入数独初盘,其中未填数的格子填上0,运行后就可得到数独的解。
图1所示标准数独是文献[3]中的失败案例,在上述程序中,通过键盘中输入数据
a=0 4 0 0 0 6 0 0 5 0 0 0 7 0 0 1 0 0 0 0 0 0 0 0 8 0 2 0 0 0 2 0 1 0 0 0 0 9 0 0 0 0 0 3 0 0 0 0 0 0 8 0 0 0 0 0 0 0 4 0 0 7 0 1 0 5 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0;
运行后得到图1所示数独的解,如图2所示,其中带圈的数字是数独初盘提供的数字(下同)。
2 变形数独的数学模型与LINGO求解程序
所谓变形数独,就是增加或改变标准数独的一些条件或规则,形成的新型数独题目。常见的变形数独有两类:一类是增加标准数独的一些条件或规则,如对角线数独、窗口数独、额外区域数独、奇偶数独等;另一类是改变标准数独的一些条件或规则,如不规则数独(锯齿数独、分区数独)、杀手数独(分组数字和数独)等。
2.1 窗口数独的数学模型与LINGO求解程序
除了标准数独的要求之外,再加上4个灰色窗口内也必须包含1~9的规定的数独,称为窗口数独,即“每行、每列及每个3×3的九宫格、每个灰色窗口都要包含数字1~9”的数独,图3就是一个窗口数独[10]。
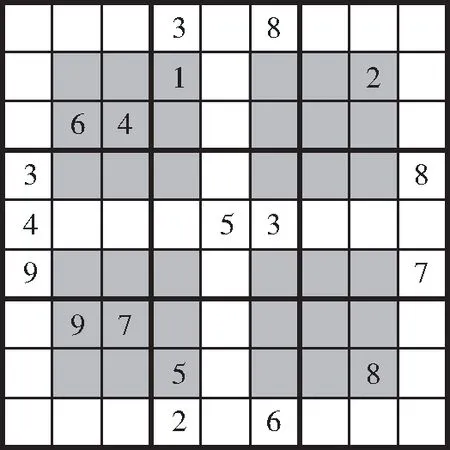
图3 窗口数独
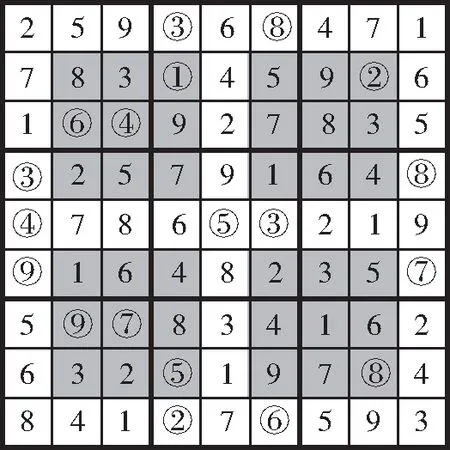
图4 窗口数独的解

在标准数独的LINGO求解程序中增加如下4个语句,就可以得到窗口数独的LINGO求解程序。
@for(number(k):(x(2,2,k)+x(2,3,k)+x(2,4,k)+x(3,2,k)+x(3,3,k)+x(3,4,k)+x(4,2,k)+x(4,3,k)+x(4,4,k))=1);
@for(number(k):(x(6,2,k)+x(6,3,k)+x(6,4,k)+x(7,2,k)+x(7,3,k)+x(7,4,k)+x(8,2,k)+x(8,3,k)+x(8,4,k))=1);
@for(number(k):(x(2,6,k)+x(2,7,k)+x(2,8,k)+x(3,6,k)+x(3,7,k)+x(3,8,k)+x(4,6,k)+x(4,7,k)+x(4,8,k))=1);
@for(number(k):(x(6,6,k)+x(6,7,k)+x(6,8,k)+x(7,6,k)+x(7,7,k)+x(7,8,k)+x(8,6,k)+x(8,7,k)+x(8,8,k))=1);
在窗口数独求解程序中,通过键盘输入数独初盘,运行后可以得到窗口数独的解。例如通过键盘输入数据:
a=0 0 0 3 0 8 0 0 0 0 0 0 1 0 0 0 2 0 0 6 4 0 0 0 0 0 0 3 0 0 0 0 0 0 0 8 4 0 0 0 5 3 0 0 0 9 0 0 0 0 0 0 0 7 0 9 7 0 0 0 0 0 0 0 0 0 5 0 0 0 8 0 0 0 0 2 0 6 0 0 0;
运行后可以得到图3所示窗口数独的解,如图4所示。
2.2 用LINGO软件编程求解额外区域数独和奇偶数独
在标准数独的基础上添加了两组额外区域(每个区域含有9个格子),在满足标准数独规则的基础上,两组额外区域上的数字一样必须是1~9,这种数独称为额外区域数独,图5就是一个额外区域数独[10];在标准数独的基础上,指定36个灰色格子,在满足标准数独规则的基础上,要求灰色格子内的数字为偶数,白色格子内的数字为奇数,这种数独称奇偶数独,图6就是一个奇偶数独[10]。

图5 额外区域数独

图6 奇偶数独
额外区域数独的特点是其额外区域的形状变化无常,奇偶数独的特点是灰色格子变化无常,因此这两种数独的数学模型及LINGO求解程序应根据具体题目具体编写。下面给出图5所示额外区域数独和图6所示奇偶数独的LINGO求解程序。
图5示额外区域数独的LINGO求解程序为:
model:
sets:
number/1..9/;line/1..9/;col/1..9/;gong/1..9/;
shudu(line,col):y,a;
link(line,col,number):x;
endsets
data:
a=0 0 0 1 0 3 0 0 0 0 3 0 0 0 0 6 0 0 0 4 0 0 0 0 0 0 0 8 0 0 0 0 0 0 9 0 4 2 0 0 0 8 0 0 0 0 0 0 0 0 1 0 0 0 0 0 2 0 0 0 0 0 6 0 0 0 5 8 0 0 0 0 0 0 8 0 0 0 3 0 1;
enddata
min=@sum(link:x);
@for(shudu(i,j)|a(i,j) #ge# 1:x(i,j,a(i,j))=1);
@for(line(i):@for(col(j):y(i,j)=@sum(number(k):k*x(i,j,k))));
@for(shudu(i,j)|a(i,j) #ge# 1:x(i,j,a(i,j))=1);
@for(line(i):@for(col(j):@sum(number(k):x(i,j,k))=1));
@for(line(i):@for(number(k):@sum(col(j):x(i,j,k))=1));
@for(col(j):@for(number(k):@sum(line(i):x(i,j,k))=1));
@for(link(i,j,k):@bin(x(i,j,k)));
@for(gong(m):@for(number(k):@sum(link(i,j,k)|3*@floor((i-1)/3)+@floor((j-1)/3)+1#eq#m:x(i,j,k))=1));
@for(number(k):(x(3,3,k)+x(3,7,k)+x(4,2,k)+x(4,4,k)+x(4,5,k)+x(4,6,k)+x(4,8,k)+x(5,3,k)+x(5,7,k))=1);
@for(number(k):(x(6,3,k)+x(6,7,k)+x(7,2,k)+x(7,4,k)+x(7,5,k)+x(7,6,k)+x(7,8,k)+x(8,3,k)+x(8,7,k))=1);
End
运行后得到额外区域数独的解如图7所示。
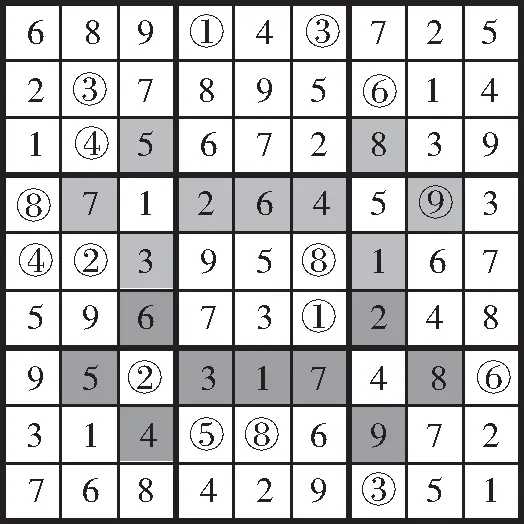
图7 额外区域数独的解

图8 奇偶数独的解
图6所示奇偶数独的LINGO求解程序为:
model:
sets:
number/1..9/;line/1..9/;col/1..9/;gong/1..9/;
shudu(line,col):y,a,t;
link(line,col,number):x;
endsets
data:
a=0 0 6 0 0 0 0 3 0 0 0 1 0 0 0 0 9 0 0 0 0 0 5 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 6 0 5 0 0 0 0 0 0 0 0 0 0 0 4 0 0 0 0 6 0 0 0 0 0 2 0 0 0 0 9 0 0 0 3 0 0 0 0 2 0 0;
enddata
min=@sum(link:x);
@for(shudu(i,j) | a(i,j) #ge# 1:x(i,j,a(i,j))=1);
@for(line(i):@for(col(j):y(i,j)=@sum(number(k):k*x(i,j,k))));
@for(line(i):@for(col(j):@sum(number(k):x(i,j,k))=1));
@for(line(i):@for(number(k):@sum(col(j):x(i,j,k))=1));
@for(col(j):@for(number(k):@sum(line(i):x(i,j,k))=1));
@for(gong(m):@for(number(k):@sum(link(i,j,k)| 3*@floor((i-1)/3)+@floor((j-1)/3)+1 #eq# m:x(i,j,k))=1));
y(1,1)=2*t(1,1);y(1,3)=2*t(1,3);y(1,6)=2*t(1,6);y(1,7)=2*t(1,7);y(2,1)=2*t(2,1);y(2,4)=2*t(2,4);
y(2,6)=2*t(2,6);y(2,7)=2*t(2,7);y(3,2)=2*t(3,2);y(3,6)=2*t(3,6);y(3,8)=2*t(3,8);y(3,9)=2*t(3,9);
y(4,2)=2*t(4,2);y(4,3)=2*t(4,3);y(4,4)=2*t(4,4);y(4,8)=2*t(4,8);y(5,2)=2*t(5,2);y(5,4)=2*t(5,4);
y(5,5)=2*t(5,5);y(5,8)=2*t(5,8);y(6,1)=2*t(6,1);y(6,5)=2*t(6,5);y(6,7)=2*t(6,7);y(6,9)=2*t(6,9);
y(7,4)=2*t(7,4);y(7,5)=2*t(7,5);y(7,8)=2*t(7,8);y(7,9)=2*t(7,9);y(8,2)=2*t(8,2);y(8,3)=2*t(8,3);
y(8,5)=2*t(8,5);y(8,9)=2*t(8,9);y(9,1)=2*t(9,1);y(9,3)=2*t(9,3);y(9,6)=2*t(9,6);y(9,7)=2*t(9,7);
@for(link(i,j,k):@bin(x(i,j,k)));@for(shudu(i,j):@gin(t(i,j)));
End
运行后得到奇偶数独的解如图8所示。
3 计算实验
运用上述程序对文献[10]中50题标准数独、50题窗口数独、50题额外区域数独、50题奇偶数独以及文献[2]中10题四级难度标准数独和4题五级难度标准数独进行求解,运算时间不超过1秒钟,正确率达到100%,对目前公认为世界难题的芬兰数独进行求解,不到1秒就能得出正确答案。
4 结语
本文根据标准数独、窗口数独、额外区域数独和奇偶数独的填数规则,充分利用LINGO软件在求解大规模规划模型的功能,编写求解数独问题的程序,用数独联盟五段段位考试训练题及《竞技数独》中的练习题进行实验,验证所编写的程序运算速度快,结论准确可靠。这种方法,一方面能够快速、准确地得到数独问题的解,另一方面培养了学生的数学建模能力,使他们掌握LINGO软件的使用技巧。我们认为,用LINGO软件编程还能求解不规则数独、杀手数独、连体数独等变形数独问题,这将是下一步研究的问题。
[1]袁新生,邵大宏,郁时烁.LINGO和Excel在数学建模中的应用[M].北京:科学出版社,2007.
[2]严德人.竞技数独[M].北京:中国言实出版社,2007.
[3]张煜东,王水花,霍元恺,等.一种基于稀疏优化的数独求解新方法[J].南京信息工程大学学报:自然科学版,2011(1): 23-27.
[4]程曦,肖华勇,吴林波.数独求解的候选数优化算法设计[J].科学技术与工程,2011(9):6409-6412.
[5]雷蕾,沈富可.关于数独问题的算法的设计与实现[J].电脑知识与技术,2007(2):481-482.
[6]王琼,邹晟.数独问题的求解、评价与生成算法的研究[J].南京师范大学学报:工程技术版,2010(1):76-79.
[7]吴涛.基于排除法填充模型的数独求解算法[J].西安航空学院学报,2014(5):11-80.
[8]胡英武.数独问题的整数规划模型[J].金华职业技术学院学报,2011(6):86-88.
[9]马丽娜.对角线数独的LINGO求解模型[J].电脑知识与技术,2015(4):91-93.
[10]数独联盟.高手数独:数独联盟段位考试训练题集(五段)[M].北京:中国水利水电出版社,2012.
Mathematical Models of Sudoku and LINGO Solution Program
KE Chun-mei
(Xiamen Ocean Vocational College, Xiamen Fujian 361101,China)
Based on the standard Sudoku rules, the ternary 0-1 variables was introduced to build a 0-1 integer programming of standard Sudoku. The LINGO solution program was developed based on the model, and its accuracy was verified by a Sudoku puzzle. Then, the solution method of standard Sudoku was extended to window Sudoku, extra area Sudoku and odd-even Sudoku. The operation time and accuracy of the LINGO programs are validated by Sudoku puzzles in the Grade Five Exam of Sudoku League. The operation time were all less than 2 seconds, and the accuracy rate were 100%, these LINGO programs can be used to solve Sudoku problems with short operation time and highly reliable results.
LINGO software; standard Sudoku; 0-1 integer programming; deformation Sudoku
2016-08-15
柯春梅(1965- ),女,讲师,硕士,从事数学建模与金融数学研究。
O141.4
A
2095-7602(2016)12-0008-06

