基于层次分析法的城市宜居性综合评价

龚 芳，陈秀明

(安徽新华学院信息工程学院，安徽合肥 230088)



基于层次分析法的城市宜居性综合评价

龚 芳，陈秀明

(安徽新华学院信息工程学院，安徽合肥 230088)

本文在宜居城市理论分析研究的基础上，从城市生活中经济富裕度、交通通达度、教育优秀度、环境优美度四个方面选取指标，构建宜居城市评价指标体系，采用层次分析法对北京、杭州、重庆、威海四个城市进行了实例分析，并对上述四个城市宜居情况做了综合评价。

宜居城市；评价体系；层次分析法

宜居城市建设是城市水平进入高质量阶段的必然，是随同城市建设过程衍生出来，而逐步被认识并开始频繁使用的概念。宜居性是城市的基本特性，城市建设的最终目的不是规模的庞大，而是身处其中的人感受如何。国内对于宜居城市这一概念的研究起始于1990年居住环境评价的研究，中国是目前世界上城市化进程发展最快的国家之一，正需探索适合中国特色的城市发展之道，以提高城市环境质量和人民生活满意度[1-2]。城市宜居性是当前国际城市发展研究的一个热点，也是目前城市居民和政府密切关注的焦点之一。

1 研究对象的基本情况

本文既考虑到城市的经济状况和城市综合知名度，也参考了近五年的国内宜居城市排行榜以及国内城市地形、地理位置等相关因素，最终确定了北京、杭州、重庆、威海四地作为研究对象。根据统计年鉴和相关资料收集到的四个城市的基本情况，可以归纳总结出以下与本文相关的数据和情况(表1～表4)。

表1 经济情况

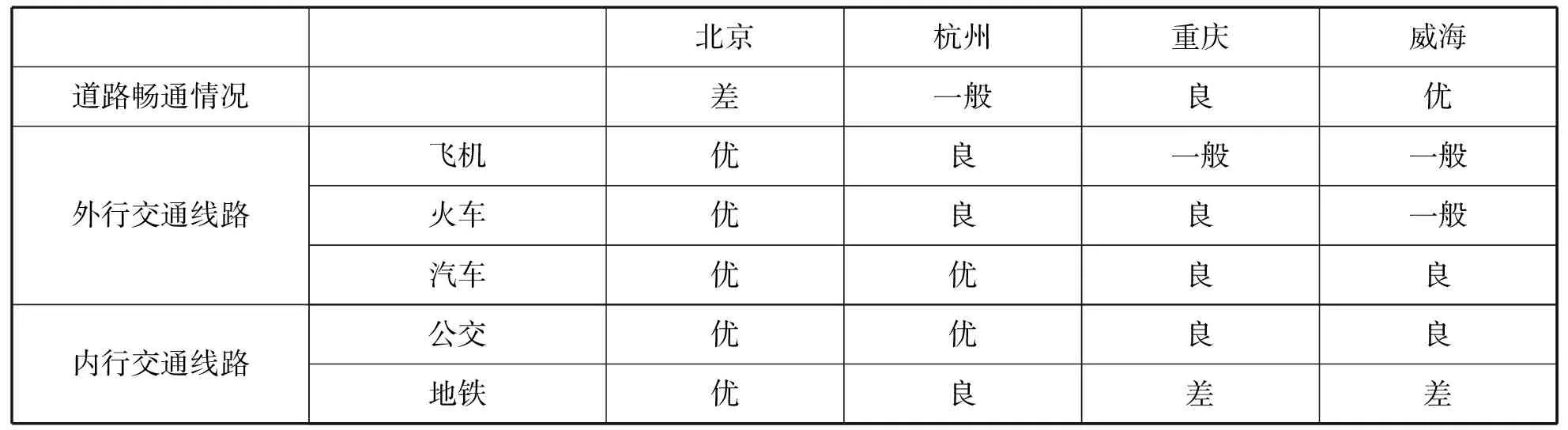
表2 交通情况

表3 学校数目

表4 环境情况数据

2 城市宜居性综合评价

2.1 指标体系及权重

本文参考了《中国城市科学研究会“宜居城市”课题组第二主干课题“宜居城市科学评价指标体系”研究组》，该文件较权威地给出了各个评价指标因素的权重，在此基础上对权重归一化处理，结果如表5所示。

表5 指标权重

2.2 层次分析法的应用

本文采用层次分析法[3-4]对四个城市的宜居性进行综合评价，具体过程如下。

2.2.1 评价指标综合排序计算

2.2.1.1 经济富裕度排序

以经济富裕度来说可以从人均GDP、城镇可支配收入、商品房价格、高校毕业生就业率四个方面来考虑，而需要排列的城市有北京、杭州、重庆、威海四地。

(1)建立层次结构即层次分析图(图1)。

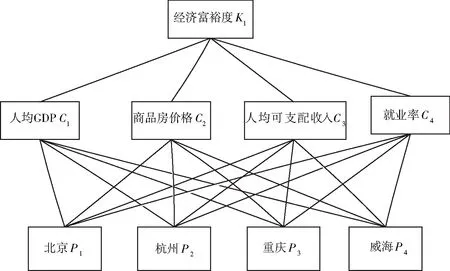
图1 层次分析图

(2)构造判断矩阵。根据上述指标权重表格可知，人均可支配收入比商品房价格和就业率稍重要，而人均GDP重要性最低，以0.5的权重差为一个范围，则相差在0到0.5之间为稍微重要，标度为3；在0.6到1之间的为稍显重要标度为5；在1.1到1.5之间的为强烈重要，标度为7；在1.6到2之间的为极端重要，标度为9，则通过计算可得出表6。

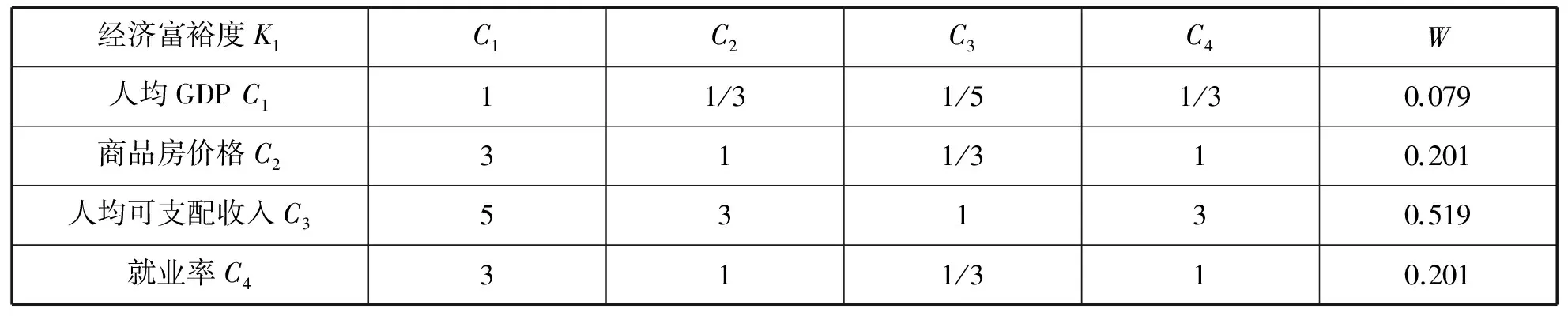
表6 判断矩阵K1—C

由以上数据可以得出矩阵：

将矩阵A的每一行正规化，得到按正规化后的判断矩阵：

将正规化后的矩阵B按行加总得到向量Wi；再将向量Wi正规化，得到W：

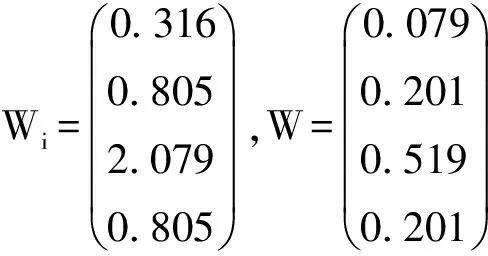
则所求特征向量为W=(0.079 0.201 0.519 0.201)T，计算判断矩阵的最大特征根：

由于CI=0.015，RI=0.90，CR=CI/RI=0.017<0.10，通过一次性检验。

同理，可得到四个城市分别关于人均GDP、房价、可支配收入、就业率四个指标的判断矩阵，并全部通过一致性检验，见表7～表10。

表7 判断矩阵

表8 判断矩阵C2—P

表9 判断矩阵C3—P

表10 判断矩阵C4—P

(3)所有判断矩阵均具有满意的一致性，则进行层次总排序，如表11所示。

表11 层次排序表

通过层次总排序，我们可以看出，根据项指标的具体数值，四种方案的优先次序为杭州、北京、威海、重庆。

2.2.1.2 交通通达度排序

在交通通达度上四个城市排序依次为杭州、重庆、威海、北京。

2.2.1.3 教育优秀度排序

四个城市的排序依次为北京、重庆、杭州、威海。

2.2.1.4 环境优美度排序

环境优美度的顺序为威海、杭州、重庆、北京。

2.2.2 城市宜居性综合评价排序

2.2.2.1 建立层次结构

用AHP对此问题进行分析，可以建立如图2所示的宜居城市方案层次分析图。

图2 层次分析图

2.2.2.2 构造判断矩阵，进行层次单排序

根据《中国城市科学研究会“宜居城市”课题组第二主干课题“宜居城市科学评价指标体系”研究组》中发布的经济、交通、教育、环境的指标权重，经济为10，交通为6，教育为3，环境为30，可以确定层次分析法的各指标的标度如下：差值1到4时标度为2，差值5到8时标度为3，差值9到12时标度为4，差值13到16时标度为5，差值17到20时标度为6，差值21到24时标度为7，差值25到28时标度为8，差值29到32时标度为9，则可得出判断矩阵如表12所示。

表12 判断矩阵 A—K

(1)由以上数据可以得出矩阵：

(2)将矩阵A的每一行正规化，得到按正规化后的判断矩阵：

(3)将正规化后的矩阵B按行加总，得到向量Wi；再将向量W正规化，得到W：

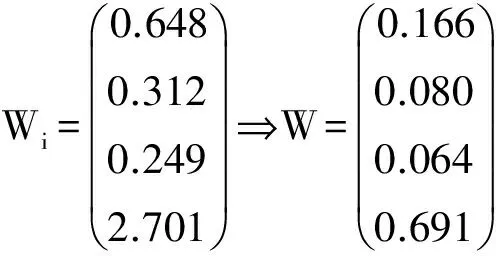
则所求特征向量为W=(0.166 0.080 0.064 0.691)T.

(4)计算判断矩阵的最大特征根：

(5)以上矩阵为四行四列矩阵，查表可知RI=0.90，可计算出CI为：

CR=CI/RI=0.049<0.10，通过一次性检验。

由以上计算可知，在经济排列中顺序为杭州、北京、威海、重庆，则这四个城市的标度为差一级则为稍微重要标度为3，差两级为稍显重要标度为5，差三级则为强烈重要标度为7，极端差则为极端重要标度为9，标度确定后层次判断矩阵如表13所示。

表13 判断矩阵K1—P

计算过程如下：

CI=0.040，RI=0.90，CR=CI/RI=0.044<0.1，通过一次性检验。

同理，可得到其余判断矩阵和计算结果，如表14～表17所示。

表14 判断矩阵K2—P

CI=0.039，RI=0.90，CR=CI/RI=0.043<0.1，通过一次性检验。

表15 判断矩阵K3—P

CI=0.039，RI=0.90，CR=CI/RI=0.043<0.1，通过一次性检验。

表16 判断矩阵K4—P

CI=0.039，RI=0.90，CR=CI/RI=0.043<0.1，通过一次性检验。

表17 宜居方案总排序

通过层次总排序，我们可以看出，根据已有数据的计算，四个城市的优先次序为威海、杭州、重庆、北京。四个城市的总体优先权权值分别为0.42、0.327、0.131和0.124。从权值可以看出，四个城市的宜居度威海最高，其次是杭州、重庆、北京。

3 结语

综上所述，本文在分析了北京、杭州、重庆、威海等城市的基本情况后，构建宜居城市的评价指标体系，采用层次分析法对四所城市的宜居度进行综合评价，评价结果客观、合理。

[1]杨敏.城市宜居性研究与评价[D].重庆:重庆师范大学,2012.

[2]张杨波.宜居城市研究局限与突破[J].湖北行政学院学报,2012(4):86-90.

[3]邓童,吕斌,张纯.基于模糊评价法的宜居社区评价研究[J].城市发展研究,2011(18):118-124.

[4]张市芳.几种模糊多属性决策方法及应用[D].西安:西安电子科技大学,2012.

[5]王若晨.关于宜居城市的拙见[J].城市建筑,2013(14):269.

[6]张建高.四川各主要城市宜居度综合评价[J].城市住宅,2015(3):118-121.

Comprehensive Evaluation of Livable City Based on the Analytic Hierarchy Process

GONG Fang,CHEN Xiu-ming

(Information Engineering College, Anhui Xinhua University, Hefei Anhui 230088,China)

Based on the theoretical analysis and research of livable city, the paper chooses the city’s economy, traffic conditions, education and ecological environment as four aspects to build livable city evaluation index system. A numerical example of Beijing, Hangzhou, Chongqing and Weihai is examined using AHP approach, and the result of comprehensive evaluation is presented in the paper.

livable city; evaluation system; analytic hierarchy process

2016-07-14

安徽省教育厅重点自然科学项目“犹豫模糊语言环境下的群推荐方法研究”(KJ2015A300)。

龚 芳(1984- )，女，讲师，硕士，从事信息资源管理与综合评价研究。

YU984

A

2095-7602(2016)12-0088-07