风电场风速对风机叶片性能影响的模拟分析

胡 斌， 刘 双

(中国特种设备检测研究院，北京 100029)



风电场风速对风机叶片性能影响的模拟分析

胡 斌， 刘 双

(中国特种设备检测研究院，北京 100029)

建立了风机叶片的三维数学模型，采用计算流体动力学软件Fluent对风机叶片流场进行了模拟分析，通过调用Static Structural模块进行叶片形变分析，并在Workbench平台下实现了流固耦合.基于该方法研究了不同风速下的流场分布情况和叶片变形情况.结果表明：本文计算值与文献[14]中的测量值吻合较好，两者最大误差不超过5%，验证了本文数学模型和计算方法的正确性；随着风速的增大，叶轮表面的速度值也在增大，气动压强分布的不均匀性更加明显；当风速由5 m/s增大至12.5 m/s时，叶片的最大形变量增大了0.91 m，叶片形变量与风速呈非线性变化关系；挥舞是叶片的主要振动形式.

风机叶片； 流固耦合； 风速； 流场； 形变

风能是一种重要的绿色可再生能源，具有良好的发展前景.近几年，我国的风电建设在逐步扩大，加强风电关键技术的研究对于提高风机运行的安全性与可靠性具有重要意义.

风机叶片是风电机组的关键部件，对于其流场研究而言，风洞试验和现场测量经费较高，风机的CFD数值模拟己成为当前国际上最活跃的研究领域之一[1].近年来，多采用数值模拟的方法研究风机叶片的流场[2-11].邱兴克[2]利用Fluent软件对风机叶片进行了二维流场分析，研究在不同风速下叶片受到的压强和表面风速的变化情况.李媛[5]建立了基于CFD的三维风机叶片模型，研究了不同风速下风轮的气动弹性特征，选用的是Sparlart-Allamaras单方程湍流模型，分析了叶片变形与载荷分布的相互影响机理.王博等[6]利用Fluent软件对多个风速工况下的风机叶片进行了气动流场模拟仿真，湍流模型为RNGk-ε，得到了压强和流速等气动参数的分布特点.张昇龙[7]利用Fluent软件对水平轴风力机进行了三维定常数值模拟，应用的湍流模型是Spalart-Allmaras单方程模型，同时对风机尾迹流场及不同截面处的压强和速度分布进行了分析.笔者建立了风机叶片的三维数学模型，采用计算流体动力学软件Fluent对风机叶片进行流场模拟分析，并调用Static Structural模块进行形变分析，在Workbench平台下实现了流固耦合，湍流模型选用SSTk-ω，主要研究了不同风速下流场分布情况和叶片变形情况，这对叶片的失效分析和运行维护将起到重要作用.

1 数学模型

选取风速作为过程参数，其具体大小见表1.由表1可见，实验模型与计算模型的转速并不相同，这是为了保证相同风速下的叶尖速比一致.设计参数见表2.几何模型如图1所示.旋转流场与外流场的网格见图2，网格总数量为2 846 019，另外旋转域采用了边界层网格，可以保证计算精度.

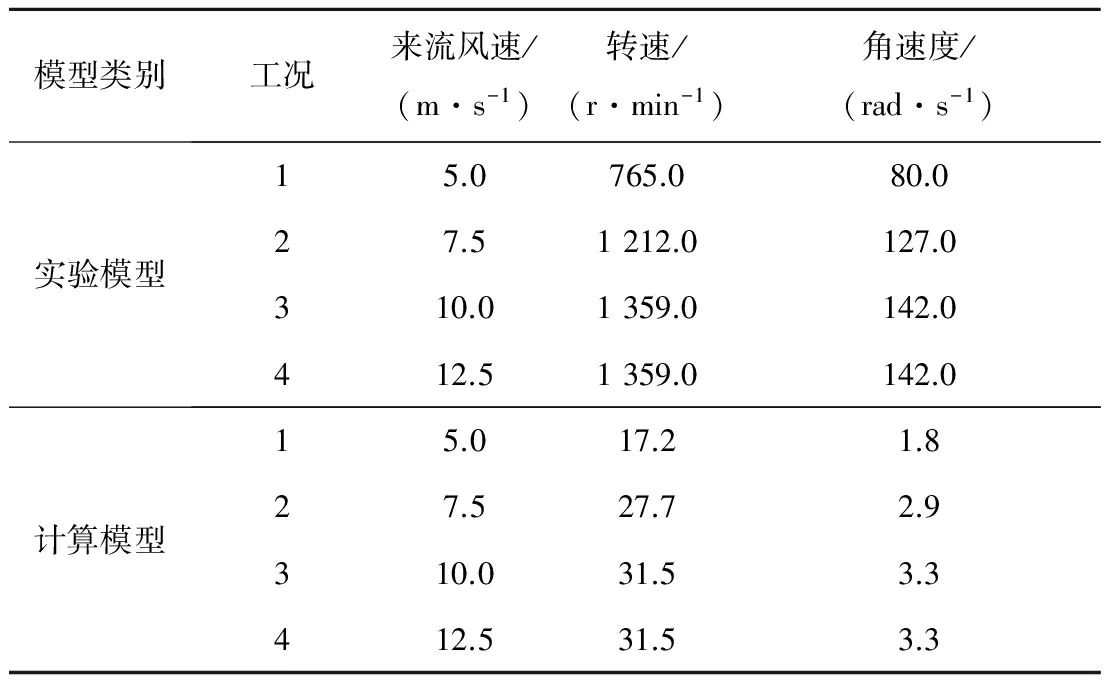
表1 过程参数

1.1 流体控制方程

连续性方程：

(1)

动量方程：

表2 风机叶片的设计参数

图1 风机叶片的几何模型

(a) 旋转流场

(b) 外流场

(2)

式中:ρ为密度;u为速度矢量;p为静压;μeff为有效黏性系数;F为体积力.

1.2 边界条件

根据风机叶片在流场中的实际运行情况，边界条件设置如下：(1)旋转域.该区域随着叶片旋转，转速为叶轮转速，定义为rotor.(2)静止域.该区域为静止外流场，定义为stator.(3)进口.即外流场来流处，定义为 velocity-inlet.(4)出口.即外流场出流处，定义为pressure-outlet.由贝兹理论可知，叶片前方远处的静压与后方远处的静压应该相等，因此设置为压力出口.(5)壁面.外流场壁面定义为wall，旋转域与静止域的交界面定义为interface，二者均采用无滑移边界条件.

1.3 模型选择与求解设置

考虑到风机的流场特点及来流条件，选择基于压力的隐式求解器进行计算，其收敛性优于分离式和显式.采用Simple方法对压力和速度进行耦合，压力插值采用Standard方式，动量和湍流动能及湍能耗散率均选用二阶离散迎风格式，有利于提高计算精度.

由于风机叶片附近流场流动情况的复杂性，选择SST(shear-stress transport)k-ω模型作为湍流模型，该模型与Sparlart-Allamaras单方程模型和RNGk-ε模型相比，对截面压力分布和转矩的预测更为准确[12]，它是标准k-ω模型的改进.使用混合函数将标准k-ε和k-ω模型结合起来，并包含转捩和剪切选项，这对边界层流动及分离流动均有较好的模拟效果[13]，因此比较适用于风机叶片的流场模拟.

SSTk-ω湍流模型方程如下：

(3)

(4)

其中有效扩散项方程：

式中:Gk、Gω分别为k与ω的湍流动能;Γk、Γω分别为k与ω的有效扩散项;μt为湍流黏性系数；Yk、Yw分别为k与w的发散项;Dω为正交发散项;Sk、Sω均为用户自定义项;k为紊流脉动动能;ω为比耗散率;ui为i向速度分量.

1.4 模型验证

为验证数学模型与计算方法的正确性，采用与实验模型尺寸相同的数学模型进行计算，将计算值与文献[14]中的测量值进行比较，结果示于图3.由图3可见，计算值与试验测量值吻合较好，且最大误差不超过5%，所以该数学模型和计算方法可用来预测风机叶片的流场分布与形变量变化.鉴于此，笔者采用相同的建模方法与计算方法对大尺寸在役风机叶片的流场分布和形变量变化进行模拟，从而提高模拟结果的可参考性.

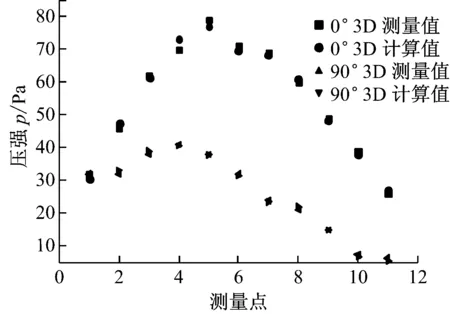
(a) 压强对比

(b) 速度对比

2 结果与分析

2.1 不同风速下的速度场分布

图4给出了叶轮的速度场分布.由图4可见，在不同的风速条件下，沿叶展方向的速度场分布趋势基本一致，轮毂处的速度值最小，叶尖处的速度值最大，这与周向速度公式v=2πR/T=ωR(式中R为风轮半径,T为周期,ω为角速度)所计算出的结果相符.从叶根到叶尖处的速度值依次增大，随着来流速度增大，叶轮表面的速度值也增大.图5为单个叶片的速度场分布，由图5可以更好地观察出这一现象.

图6给出了叶轮后截面的速度场分布.距离叶轮中心3 m的位置，由于叶轮前截面的流场并未受到叶轮的阻碍作用，速度场不会发生明显变化，因此主要分析了叶轮后截面的速度场分布.由图6可以看出，叶轮的旋转会影响到周围区域的流体流动，导致叶轮附近区域流体速度相对较大，而远离叶轮区域的流体速度相对较小.另外，由图6还可以看出，随着来流速度的增大，叶轮影响区域的速度值也增大，而且具有紊流现象，符合实际流场的空气流动特性. 图7给出了速度场分布矢量图.从图7可以直观地看出叶片在旋转过程中流场的分布特性.叶尖处速度值较大，而且在旋转过程中，叶轮主要受哥氏力和离心力的影响.哥氏力引起逆压力梯度降低，使得流域出现附加的加速流动，而离心力促使吸力面上分离区域的气流沿叶尖方向移动，在这2种力的共同作用下，流动分离延迟，同时气流的稳定性增强，这样可起到增大升力和减小阻力的效果，从而增强了风机的动力输出，保证在额定工况下满足功率输出要求.通过对不同工况下叶片性能的分析，对本文中的风机进行了风机效率计算，风机效率随转速变化的曲线见图8.由图8可见，当风速为10 m/s时，风机的气动效率较好；当风速继续增大时，风机输出功率保持恒定后有所降低.

(a) 5 m/s

(b) 7.5 m/s

(c) 10 m/s

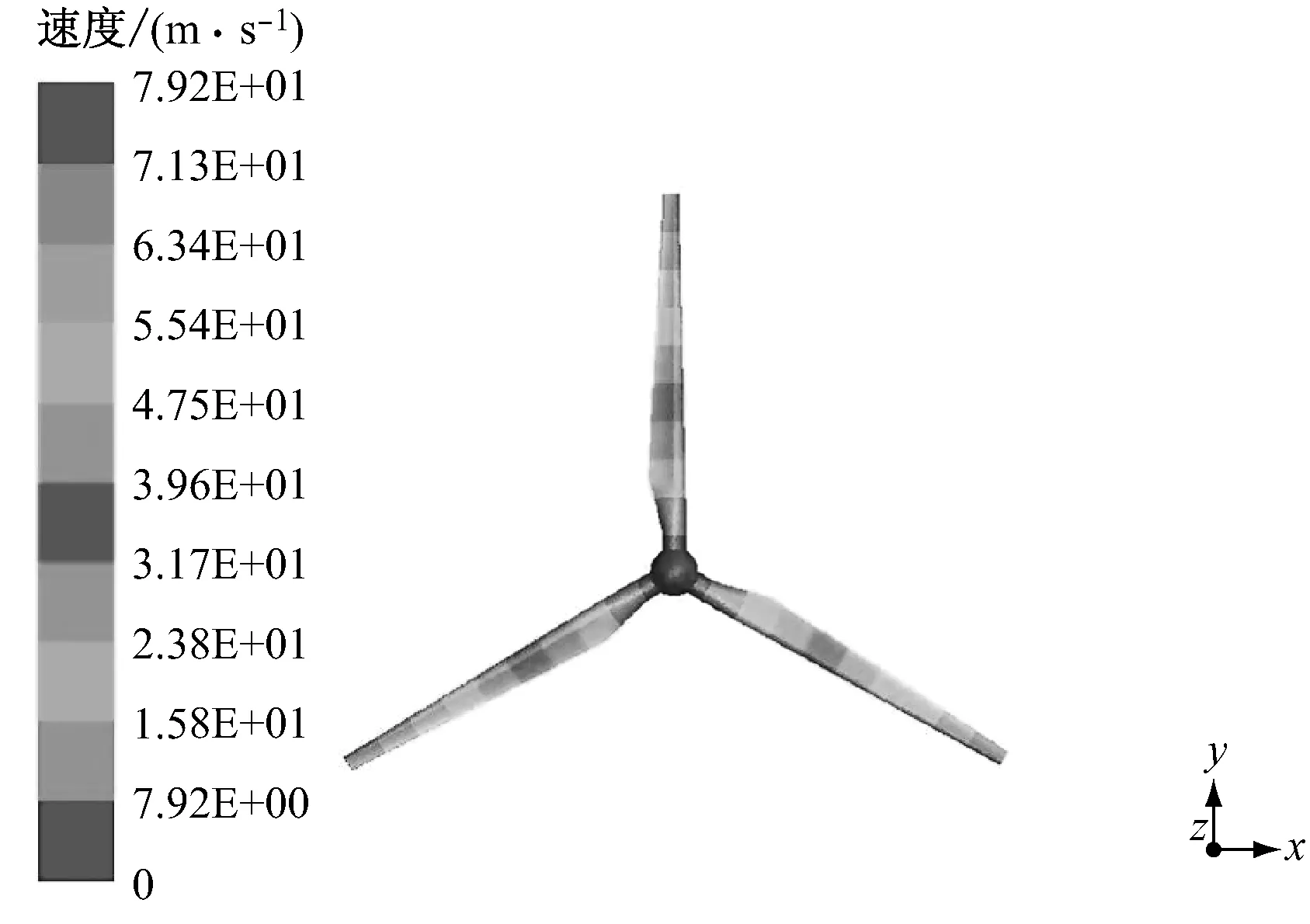
(d) 12.5 m/s

2.2 不同风速下的压强分布

图9给出了叶轮的压强分布.由前文分析可知，叶轮前截面的压强分布均匀，因此主要分析叶轮后截面的压强分布.由图9可以看出，在叶轮的旋转作用下，叶片周围区域的空气气流速度受到影响，使叶轮及周围区域的气流压强随之发生变化，呈现出与速度场相呼应的分布特点.随着风速的增大，紊流现象更加强烈，导致叶片表面流场发生较大变化，故气动压强分布表现出明显的不均匀性.图10给出了单个叶片的压强分布,从图10可以看出叶片根部压强相对较大.

(a) 5 m/s

(b) 7.5 m/s

(c) 10 m/s

(d) 12.5 m/s

(a) 5 m/s

(b) 7.5 m/s

(c) 10 m/s

(d) 12.5 m/s

图7 不同风速下叶轮速度场分布矢量图

Fig.7 Velocity vector field distribution at different wind speeds

图8 风机功率随风速的变化曲线

2.3 不同风速下的形变分析

图11给出了不同风速下叶片在旋转过程中发生的形变.叶片由静止到旋转过程中，所受的外力逐渐增大，进而使叶片发生形变.随着风速的增大，形变量也逐渐增大，当风速由5 m/s增大到12.5 m/s时，形变量由0.15 m增大到1.06 m，显然形变量是比较大的.值得一提的是，形变量与风速呈非线性变化，如图12所示.由图11(b)也可以发现，在风载的作用下，叶片在垂直于旋转平面方向上发生了弯曲振动，从而也体现出挥舞是叶片的主要振动形式，挥舞形式的振动对叶片的整体结构相当不利，是造成疲劳损伤的重要原因之一.

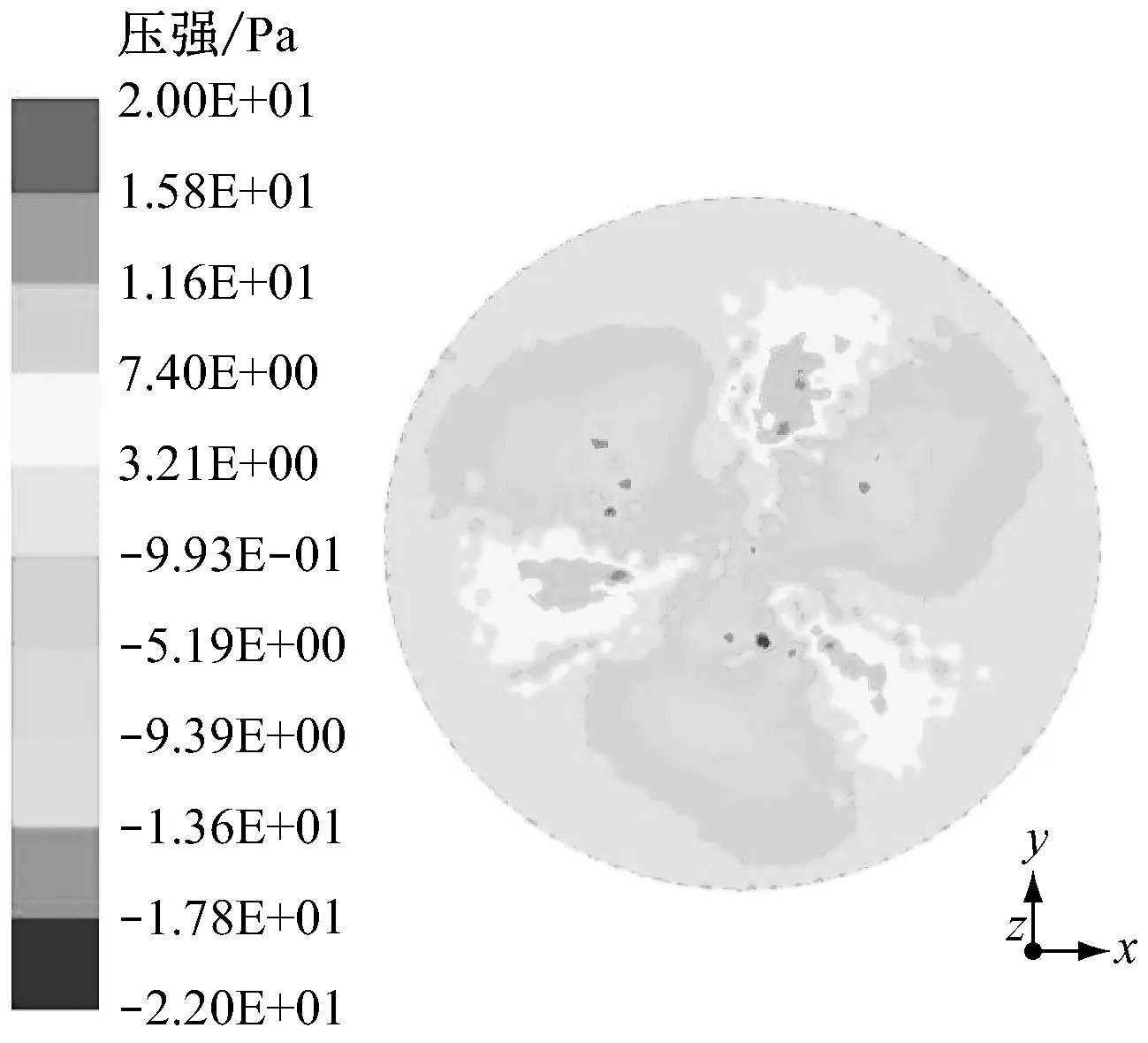
(a) 5 m/s

(b) 7.5 m/s

(c) 10 m/s

(d) 12.5 m/s

图10 叶片压强分布

3 结 论

(1)通过对风机叶片在不同风速下的模拟分析，得到了相应风速下的叶轮速度场和压强分布.随着风速的增大，叶轮表面的速度值增大，气动压强分布的不均匀性更加明显.当风速为10 m/s时，风机的气动效率较好.

(2)叶片的形变量随风速变化呈非线性变化.在风载的作用下，叶片在垂直于旋转平面方向上会发生弯曲振动，说明挥舞是叶片振动的主要形式，挥舞形式的振动对叶片结构的稳定性造成不利影响.

(a) 5 m/s

(b) 7.5 m/s

(c) 10 m/s

(d) 12.5 m/s

图12 不同风速下叶片形变量的大小

[1] 刘丹, 李军向, 薛忠民, 等. 风力发电机叶片数值模拟综述[J]. 电气技术, 2010(7): 7-11, 18.

LIU Dan, LI Junxiang, XUE Zhongmin,etal. The review of numerical simulation of wind turbine blade[J]. Electrical Engineering, 2010(7): 7-11, 18.

[2] 邱兴克. 风力发电机三维建模与分析[D]. 乌鲁木齐: 新疆大学, 2006.

[3] 魏义利. 大型风力机叶片的外形设计与数值模拟分析[D]. 大连: 大连理工大学, 2010.

[4] 戴彬彬. 风力机叶片优化设计与流固耦合特性研究[D]. 湘潭: 湘潭大学, 2013.

[5] 李媛. 风力机叶片流固耦合数值模拟[D]. 北京: 华北电力大学, 2013.

[6] 王博, 祁文军, 孙文磊, 等. 风力发电机叶片气动性能数值模拟[J]. 机床与液压, 2013, 41(7): 166-171.

WANG Bo, QI Wenjun, SUN Wenlei,etal. Numerical simulation of aerodynamic performance for wind turbine blades[J]. Machine Tool & Hydraulics, 2013, 41(7): 166-171.

[7] 张昇龙. 水平轴风力机尾流场及其气动性能的研究[D]. 兰州: 兰州理工大学, 2014.

[8] LI Yuwei, PAIK K J, XING Tao,etal. Dynamic overset CFD simulations of wind turbine aerodynamics[J]. Renewable Energy, 2012, 37: 285-298.

[9] YU D O, KWON O J. Predicting wind turbine blade loads and aeroelastic response using a coupled CFD-CSD method[J]. Renewable Energy, 2014, 70: 184-196.

[10] KOÇ E, YAVUZ T, KILKIB,etal. Numerical and experimental analysis of the twin-blade hydrofoil for hydro and wind turbine applications[J]. Ocean Engineering, 2015, 97: 12-20.

[11] LI Y, CASTRO A M, SINOKROT T,etal. Coupled multi-body dynamics and CFD for wind turbine simulation including explicit wind turbulence[J]. Renewable Energy, 2015, 76: 338-361.

[12] 刘磊, 徐建中. 湍流模型对风力机叶片气动性能预估的影响[J]. 工程热物理学报, 2009, 30(7): 1136-1139.

LIU Lei, XU Jianzhong. The effects of turbulence model on the aerodynamic performance prediction of wind turbine blade[J]. Journal of Engineering Thermophysics, 2009, 30(7): 1136-1139.

[13] 钟伟, 王同光. 转捩对风力机翼型和叶片失速特性影响的数值模拟[J]. 空气动力学学报, 2011, 29(3): 385-390.

ZHONG Wei, WANG Tongguang. Numerical analysis of transition effect on stall performance of wind turbine airfoils and blades[J]. Acta Aerodynamica Sinica, 2011, 29(3): 385-390.

[14] 王久鑫. 水平轴风力机尾流结构及其性能的实验研究[D]. 兰州: 兰州理工大学, 2014.

Influence of Wind Speed on the Performance of Wind Turbine Blades

HU Bin, LIU Shuang

(China Special Equipment Inspection and Research Institute, Beijing 100029, China)

Based on the three-dimensional mathematical model of wind turbine blade, a simulation analysis was carried out on the turbine flow field using CFD software Fluent, while a stress analysis of the blade was performed with Static Structural module, in which case fluid-solid coupling was realized in the Workbench platform. The method proposed was used to study the flow field and stress distribution of wind turbine blades at different wind speeds. Results show that the calculated values agree well with actual measurements in literature [14], and the maximum error is less than 5%, proving the calculation method and mathematical model to be correct. With the rise of wind speed, the velocity on impeller surface also increases, and the pressure distribution becomes obviously non-uniform. When the wind speed rises from 5 m/s to 12.5 m/s, the maximum deformation of blade would be increased by 0.91 m, and the blade deformation is nonlinearly related to the wind speed. The vibration of blade is mainly in the wave form.

wind turbine blade; fluid-solid coupling; wind speed; flow field; deformation

2015-12-15

2016-03-01

国家质检公益性行业科研专项基金资助项目(201210076)

胡 斌(1977-)，男，河南信阳人，高级工程师，硕士研究生，研究方向为无损检测与安全评价. 电话(Tel.)：010-59068300;E-mail：hubin@csei.org.cn．

1674-7607(2016)12-0993-07

TK83

A 学科分类号：470.30