利用遗传算法进行离心压缩机整级优化设计

程 超， 秦国良

(1．西安交通大学 能源与动力工程学院，西安 710049；2．西安陕鼓动力股份有限公司，西安 710075)



利用遗传算法进行离心压缩机整级优化设计

程 超1,2， 秦国良1

(1．西安交通大学 能源与动力工程学院，西安 710049；2．西安陕鼓动力股份有限公司，西安 710075)

建立了离心压缩机整级的物理损失模型，编制用于离心压缩机整级性能参数优化的遗传算法程序，并对优化前后该离心压缩机整级性能进行了数值模拟分析，以证实损失模型的可靠性以及将CHC遗传算法引入离心压缩机级性能参数优化的可行性.结果表明：与优化前相比，优化后整级的性能得到了一定程度的提升，级内流动更加合理，消除了分离，减少了损失.

离心压缩机； 遗传算法； 参数优化； 整级设计

众所周知，压缩机在国民经济建设中发挥了重要作用，被称为能源工业的心脏，在能源日益紧缺的今天，开发和研究高效率的离心压缩机以减少能源消耗就显得尤为重要.目前,离心压缩机的设计[1-3]大多是针对某一具体部件的，如进口部分、叶轮内部、扩压器、弯道、回流器和蜗壳等，这样既可以对所研究的部件有深入的认识，而且随着计算流体力学(CFD)数值模拟技术的快速发展，通过对流场进行数值模拟，可以详细考虑形状参数对该部件性能影响的程度.但同时也有可能产生其他一系列相关问题，如虽然各部件的优化程度都较好，但是各部件之间的匹配可能出现不协调；各部件优化所采用的标准也不一样，如何将其结合起来以达到预期的性能等.压缩机整体性能涉及的范围较广，国内外也有一些研究成果，但是多部件组合复杂性的存在使得问题变得复杂.针对压缩机整级性能优化设计[4-15]的方法比较多，主要的难点有：(1)构造适当的物理模型，物理模型必须合理而且有足够的精确度；(2)提供最优化函数，也就是按照所构造的物理模型找到合理的性能函数，性能函数的自变量就是所要优化的参数；(3)采用的优化算法必须高效，全局和局部收敛性都较好.

遗传算法[4]是一种鲁棒性很好的优化算法，起于20世纪五六十年代，其基本思想是通过使用类似于自然遗传选择和变异的操作算子，不断进化一群候选解，最终得到问题的最优解或满意解.其涉及到5大要素：参数编码、初始群体的设定、适应度函数的设计、遗传操作的设计和控制参数的设定.近年来，由于遗传算法在全局方面的收敛性很好，该算法得到了充分的发展.其中CHC遗传算法是Eshelman于1991年提出的一种改进的遗传算法，第一个C代表跨世纪精英选择(Cross generational elitist selection)策略，H代表异物种重组(Heterogeneous recombination)，第二个C代表大变异(Cataclysmic mutation).在选择时，上一代的种群与通过新交叉方法产生的新种群混合，从中按一定概率选取较优个体，在交叉时，仍采用均匀交叉方法，在变异时，进化前期不采取变异操作，当种群进化到一定收敛时期后，从优秀个体中选择一部分个体进行初始化，初始化是通过选择一定的比例来随机决定它们的位置.

笔者建立了离心压缩机级的物理损失模型，并以该损失模型为基础构造以效率为适应度值的适应度函数，引入CHC遗传算法对该适应度函数求最优解，从而将离心压缩机级参数优化问题转化为求解适应度函数最大值的问题，计算结果表明优化后的级参数能使适应度函数达到最大值，也就是使效率达到最高，最后通过数值计算验证了优化结果的合理性.

1 损失模型的建立

离心压缩机损失的计算是不断发展的，不同时期对损失的认识不同，处理方法也不一样.从物理机理上可以把离心压缩机整个中间级的损失体系分为4部分[3]：叶轮内部损失、叶轮外部损失、扩压器损失以及弯道和回流器损失.

叶轮内部损失包括叶轮表面摩擦损失Δqsf、叶轮叶片载荷损失Δqbl、叶片尾流混掺损失Δqmi和叶轮前盘间隙损失Δqcl(闭式叶轮不存在该项损失)；叶轮外部损失包括圆盘摩擦损失Δqdf、叶轮边缘回流损失Δqre以及叶轮轮盖的泄露损失Δqlk；扩压器损失包括无叶段损失Δqld、叶片扩压器损失Δqd和出口损失Δqex；弯道和回流器损失Δqtb则主要考虑到弯道和回流器里的摩擦损失和分离损失等.各项损失的求解公式详见相关资料[1-3]，下面着重描述叶轮叶片载荷损失.

叶轮叶片载荷损失可采用简化的边界层理论方法，从叶片表面边界层动量厚度的计算求得总压损失，进而求得压头损失.由湍流边界层的冯·卡门方程作为出发的基本方程，可以得到沿叶片的积分动量厚度近似为

(1)

式中：θ为边界层动量厚度；l为计算点距叶片前缘的距离；wmax和wmin分别为气流沿叶片表面速度的最大值和最小值.

总压损失近似表示为

(2)

式中：Z为叶片数；θ2为叶轮出口处的边界层动量厚度；r2为叶轮出口半径；g为重力加速度；ρ为气流密度；w2为气流在叶轮出口处的相对速度.

将式(1)代入式(2)可得出对于整个叶轮通道的无量纲叶片载荷损失：

(3)

式中：ws1为叶轮进口处气流在轮盘侧的相对速度；u2为叶轮出口圆周速度；lb为流动长度[3].

由于损失模型中包含了叶片表面速度分布的求解，所以为了尽快得到叶片表面的速度分布，又不能在精度方面降低标准，就采用了通流模型理论，利用流线曲率法对叶片内的三维流场进行求解，以获得叶片表面的速度分布.目前，工程界通用的通流模型理论是在平均s2m流面流动分析的基础上进行一组s1回转流面的分析来作为三元流动的近似解，将叶型的中心面近似当成平均s2m流面处理，主要考虑的是s1回转流面的流动情况，因此相对速度求解公式如下：

(4)

式中：β为流面上的流动角；φ为子午流线倾角；r为半径；θ、m分别代表圆周方向和子午流线方向.

最终采用式(3)和式(4)就可以顺利求解出叶轮叶片载荷损失.

2 适应度函数的建立

综上所述，离心压缩机整级的内部损失∑qin和外部损失∑qex的表达式如下：

∑qin=Δqsf+Δqbl+Δqmi+Δqcl+Δqld+Δqd+Δqtb

(5)

∑qex=Δqdf+Δqre+Δqlk

(6)

总效率ηov被定义为

(7)

其中，Δpth为对应于叶顶速度平方的无量纲化理论压头，表达式为

(8)

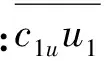
(9)

其中，滑移率σ由Eckert的经验公式给出：

(10)

式中：r1为叶轮进口半径.

将推导出的总效率表达式作为适应度函数，选定二进制编码，采用CHC遗传算法，给定具体的参数优化区间就能进行求解，得出所需的5大要素.

图1和图2为详细的程序流程图.

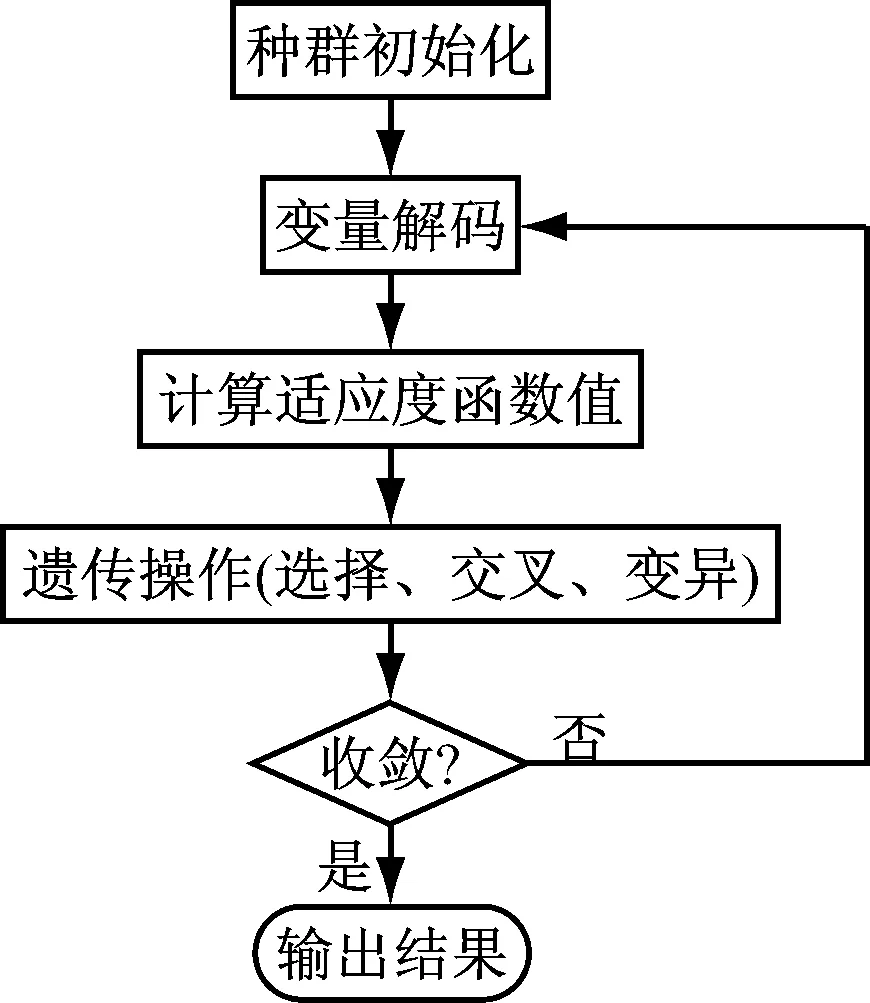
图1 程序流程

3 优化过程

利用损失模型和CHC遗传算法，编制Fortran程序对某工程项目用离心压缩机的级进行了优化.

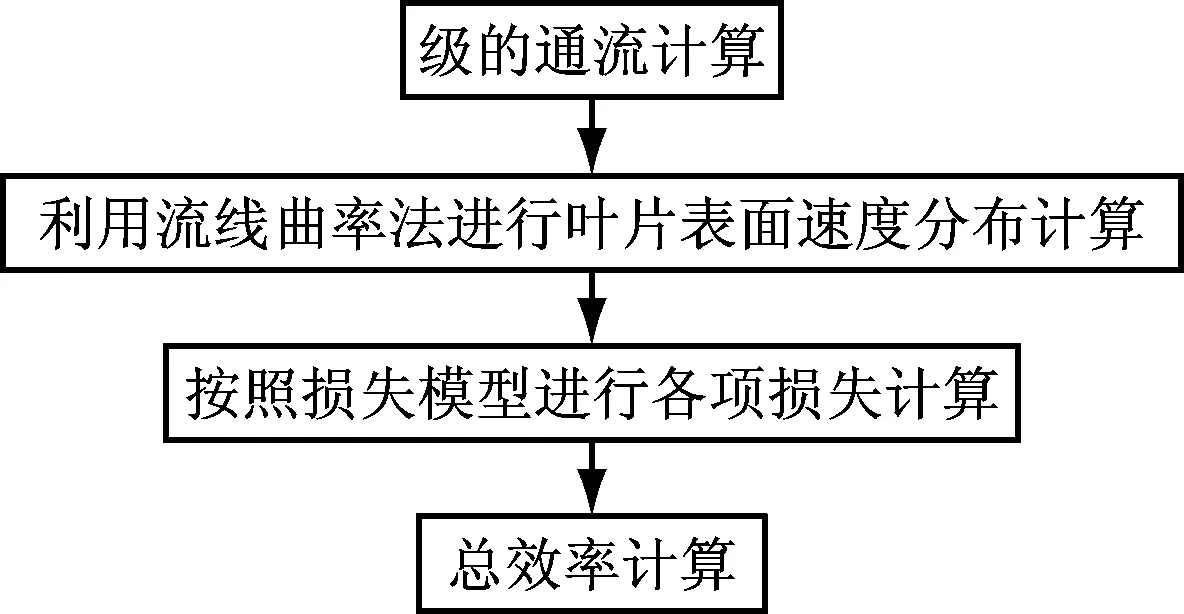
图2 数学模型流程

该离心压缩机的级为20世纪80年代从国外引进，叶轮叶片为三维直纹面叶型，扩压器和回流器叶片为二维圆弧形结构.级进口气流参数为：进口压力pin=0.10 MPa，进口温度Tin=300 K，进口密度ρin=1.158 kg/m3，进口体积流量qV,in=1.45 m3/s，转速n=13 860 r/min.

首先设置该级的几个主要参数：叶轮外径D2、叶轮叶片出口安装角β2A、轮盖密封直径Ds、叶轮叶片数Z、轮盖密封间隙S、叶片扩压器的叶栅稠度(l/t)i(t为两叶型周向的间距)、回流器的叶栅稠度(l/t)b、叶轮叶片厚度δ1、叶片扩压器叶片厚度δ2、回流器叶片厚度δ3等，这些参数在优化过程中保持不变，如表1所示.

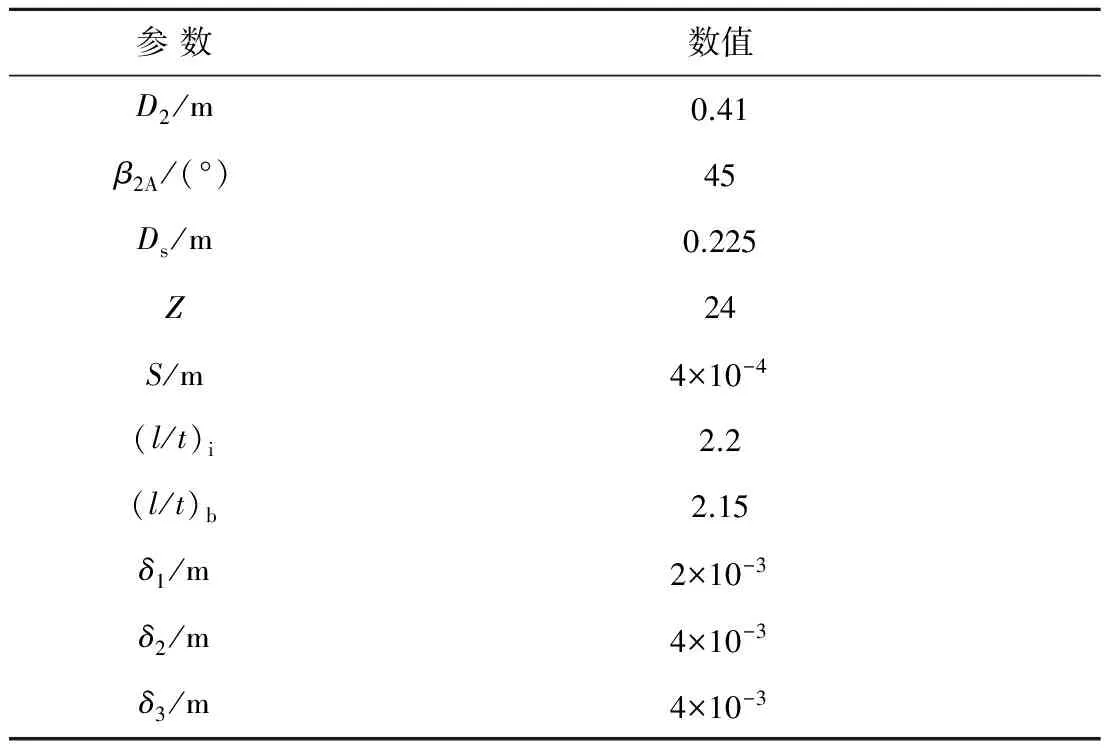
表1 固定参数

综合考虑各参数对级性能的影响, 选定8个待优化的参数：轮毂直径比d/D2、速度系数Kc、叶轮叶片冲角i、叶片扩压器的折转角Δα、叶道进口直径比D1/D2、无叶扩压段的出口直径比D3/D2、叶片扩压器出口直径比D4/D2和流量系数Ψ2r.这些参数的优化区间见表2.

表3给出了参数优化后的结果，其中初始值为级优化前的值.从表3可以看出，优化到60代时的参数与优化到150代时的参数基本一致，说明该算法能迅速收敛得到最优值，同时优化后级的总效率提高了2.24%.从优化前后叶轮参数的变化可以看出，优化后的d/D2小于优化前的d/D2，而叶轮中的损失与气流在叶片进口相对速度(W1)的平方成正比，d/D2增大使得W1增大，因此优化后的叶轮通过减小d/D2可以提高叶轮效率.徐忠[1]通过不同轮毂直径比下叶轮的级性能曲线指出，叶轮效率确实随轮毂直径比的增加而降低.优化后的叶轮轮盖进口段的曲率(r/b1)远大于优化前的曲率，这样可以大大改善轮盖转弯处气流速度的不均匀性，提高叶轮效率；速度系数Kc接近于1，实验证明Kc接近于1有利于提高叶轮效率[1]；优化后的叶道进口直径比D1/D2大于优化前的D1/D2，有利于减少叶道长度，从而减少摩擦损失，提高叶轮效率；叶片扩压器出口直径D4和叶片扩压器的折转角Δα共同决定了其出口面积，经过计算得出优化后的叶片扩压器出口面积比优化前的叶片扩压器出口面积大，也就是说扩压程度提高，有利于提升级压力，而且优化后的Δα变小还可以防止吸力面上气流的分离[1].

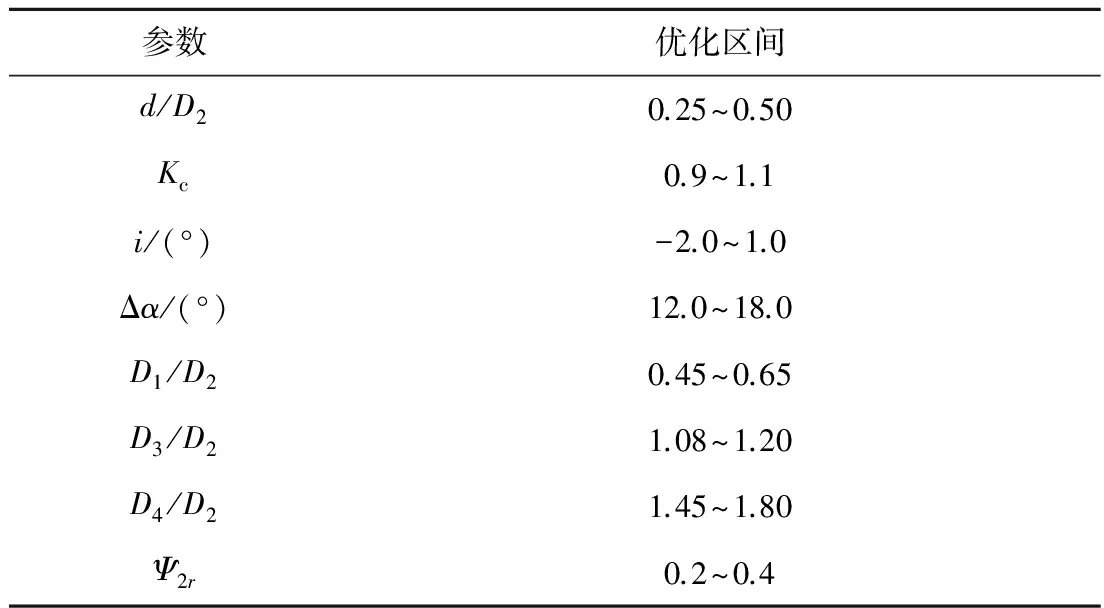
表2 参数优化区间

表3 参数优化结果的比较

4 数值模拟验证

为了深入验证损失模型的优化效果，采用商业软件Numeca对优化前后离心压缩机级内的流动进行数值模拟计算.由于叶轮机械的周期性，对叶轮流道、叶片扩压器流道和回流器流道进行单通道求解.所有流道采用Autogrid划分网格，最后在IGG里进行网格设置.叶轮流道、叶片扩压器流道和回流器流道的网格数分别为40万、30万和30万，总网格数为100万，所有网格均为六面体结构化网格.

湍流模型采用标准k-ε模型，空间差分采用二阶精度的中心差分格式，时间项采用4阶Runge-Kutta方法迭代求解.入口边界条件为在0-0截面处给定总压、总温及流动方向，出口边界条件为回流器出口6-6截面处给定质量流量.动/静交接面采用周向平均法进行相关物理量的传递，最后利用euranus求解器求解三维定常Navier-Stokes方程组.优化前后，计算收敛时的进、出口质量流量残差均小于0.1%.

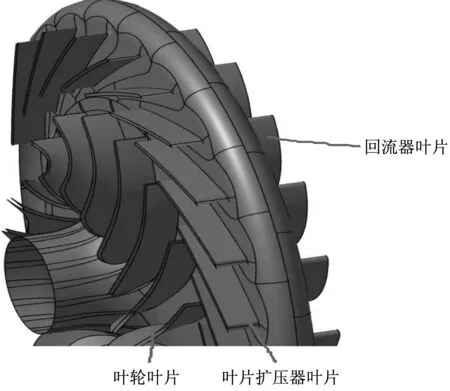
图3 整级模型图

从表4可以看出，优化后的级在同样的流量系数下，总压多变效率提升了2.36%，总能头系数增大了4.29%.为了更有效直观地观察优化前后离心压缩机级的性能变化，对优化前后的子午流面和50%叶高处的流面进行对比分析，结果如图5～图10所示.图中左、右分别为优化前和优化后的流场.

从图5可以看出，优化后级的进口静压分布更加均匀，通过叶轮旋转对气流做功，级优化后的叶轮出口静压有一定提升，然后气流在扩压器中将大部分的动能转化为压力能，由于级优化后扩压器的扩压能力得到了有效提升，其优化后的出口静压大约是优化前的1.053倍，进而增大了级的总能头系数，同时气流在扩压器、弯道和回流器中的静压分布更加均匀，沿流线方向和叶片高度方向的压差变化小，只是在回流器盖盘处局部有低压力区存在，表明气流经过该处时并没有放散扩压，而是处于收敛减压，因此回流器盖盘半径可以适当放大，以提升该处的压力，便于与主流压力保持一致.

图4 整级网格分布图

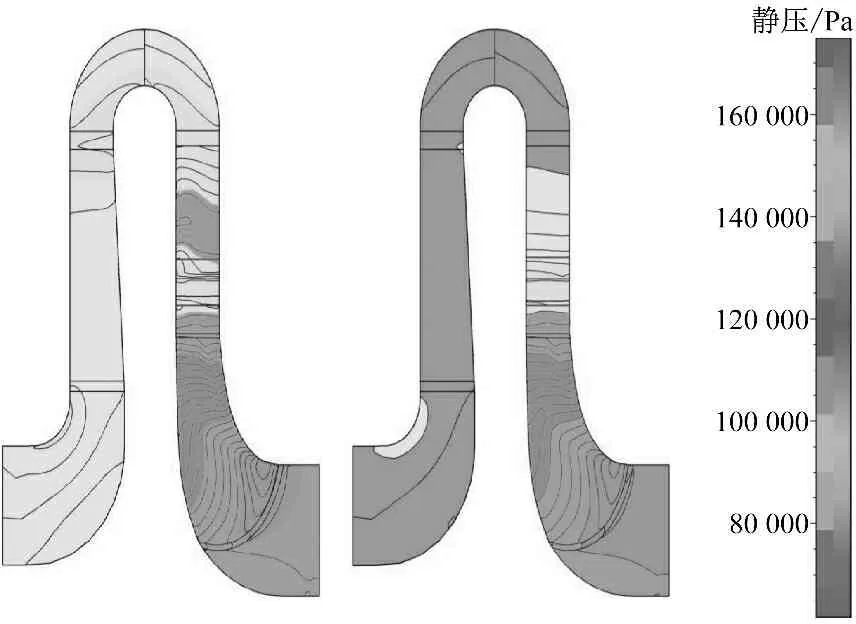
图5 子午流面优化前后静压分布

从图6可以看出，级在优化前后的扩压器中静温变化较大，温差大约为5 K，优化前气流的静温提升主要在弯道和回流器中，而气流经过弯道和回流器时并没有提升压力，因此气流静温的提升表明气流存在较大损失，而优化后气流的静温提升直接在扩压器中就实现了，在弯道和回流器中出口静温变化很小，这也充分说明级优化后气流在扩压器中的动能大幅减小，在后面的弯道和回流器中并没有产生很大的摩擦损失，因而对级效率的提升起到重要作用.

图6 子午流面优化前后静温分布

Fig.6 Static temperature distribution on meridional flow surface before and after optimization

图7为优化前后叶轮通道内50%叶高处气流的相对马赫数分布.从图7可以看出，优化后通过增大叶轮进口面积，降低了叶轮叶片进口的相对马赫数，叶轮叶片进口气流的冲击损失减少，气流均匀性有所改善，其在叶片内部流动时的流动状况也有所改善.一般来说，气流在叶片内部流动时相对速度减小，绝对速度增大，优化前靠近叶片出口吸力面区域存在大量相对速度很小的流体，阻碍气流顺利流出叶轮通道，而优化后靠近叶片出口的气流相对马赫数有所提高，避免在叶片出口存在大量低能涡，为气流进入扩压器创造了较好的流动条件.

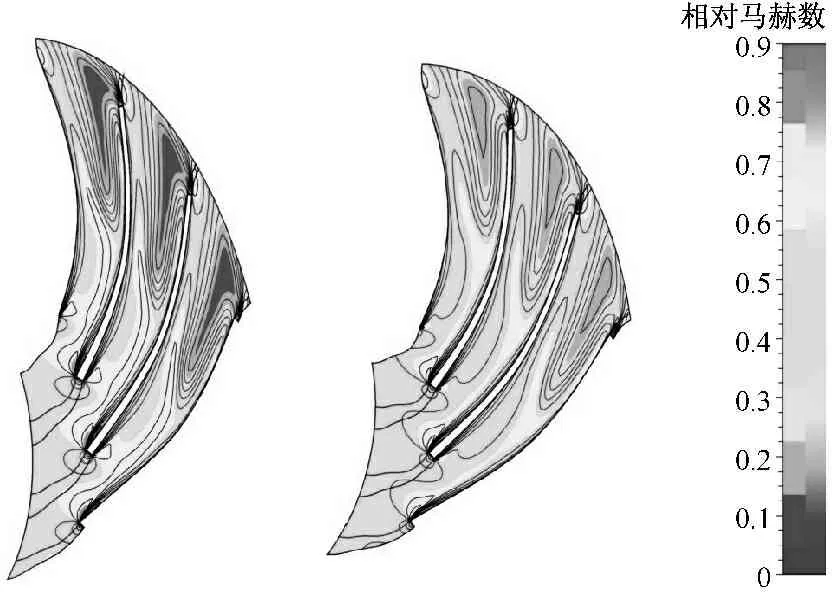
图7 优化前后叶轮通道内50%叶高处流面的相对马赫数分布

Fig.7 Relative mach number distribution at 50% blade height of impeller before and after optimization

图8为优化前后叶轮通道内50%叶高处气流的相对速度流线分布图.从图8可以看出，优化前，叶片吸力面尾部有部分涡旋产生，表明由于相对速度减小过快，更多的主流受到壁面黏性影响，动能不足以摆脱边界层的黏性，使得叶片吸力面的边界层增厚，主流向压力面偏移，同时该边界层低能涡会与叶片尾迹低能涡相互掺混，流动趋于恶劣.优化后，流动状况大为改善，不仅减小了叶片吸力面尾部边界层，而且降低了叶片尾迹区域对流动的恶劣影响，提高了叶片出口气流的均匀性，有利于改善气流在后续扩压器中的流动状况.

图8 优化前后叶轮通道内50%叶高处相对速度流线的分布

Fig.8 Relative velocity streamline at 50% blade height of impeller before and after optimization

图9为优化前后扩压器通道内50%叶高处气流绝对速度的流线分布图.从图9可以看出，优化前由于叶片扩压器的折转角过大，导致气流在扩压器中流动时，较短的流程里需要实现较大幅度的扩压，气流容易产生扩压损失，因而在扩张度最大的叶片背弧中部产生尾涡，该尾涡的影响区域较大，而且与尾迹气流相互影响，使流动效率降低；优化后气流在扩压器中的流程变长，叶片扩压器的折转角减小，气流在扩压器中扩压比较均匀，避免了流动扩压分离，流动效率较高.

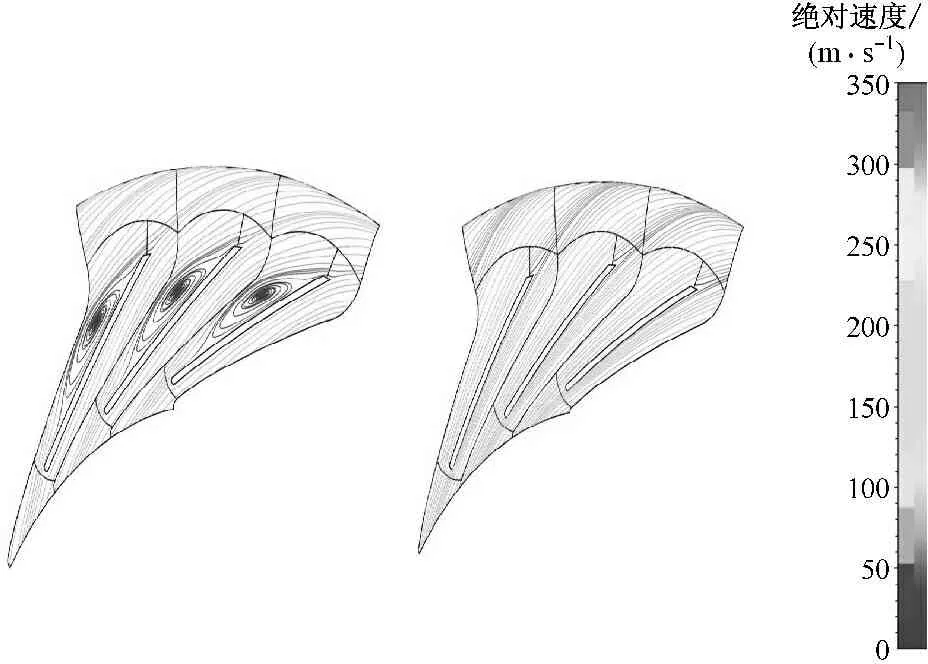
图9 优化前后扩压器通道内50%叶高处绝对速度的分布

Fig.9 Absolute velocity distribution at 50% blade height of diffuser before and after optimization

图10为优化前后回流器通道内50%叶高处气流绝对速度的流线分布图.从图10可以看出，优化前进入回流器的气流进口速度偏大，容易造成较大的流动损失，而优化后的回流器气流进口速度小，流动损失小，流动效率高.

图10 优化前后回流器通道内50%叶高处绝对速度的分布

Fig.10 Absolute velocity distribution at 50% blade height in return channel before and after optimization

从图5～图10可以看出，通过级的优化，可以改善级内各部件的匹配，使得气流在级内的流动更加合理，消除了分离，减少了损失，提高了整个级的流动效率.

5 结 论

(1)建立了离心压缩机级的物理损失模型，根据损失机理对各项损失进行了分类与分析，得出各项损失的计算公式，针对损失模型精确计算所需的速度分布，引入准三维方法即二类相对流面(s1/s2m流面)法，并最终通过流线曲率法进行速度分布求解，使得损失模型的精确计算变为可能.

(2)以所建立的损失模型为基础，构造了以效率为适应度值的适应度函数，通过编制相关程序将CHC遗传算法引入到离心压缩机级的参数优化中，对其进行参数优化，计算结果表明优化后的级参数能使适应度函数达到最大值，即效率达到最高，验证了损失模型和基于离心压缩机级参数优化的遗传算法的优越性.

(3)通过数值计算方法对优化前后离心压缩机的级进行了内部流动特性分析，计算结果表明级的优化有效改善了级内各部件的匹配，使得气流在级内的流动更加合理，消除了分离，减少了损失，提高了整个级的流动效率.

[1] 徐忠.离心压缩机[M].西安：西安交通大学出版社，1990.

[2] 王尚锦.离心压缩机三元流动理论及应用[M].西安：西安交通大学出版社，1991.

[3] 沈天耀.离心叶轮的内流理论基础[M].杭州：浙江大学出版社，1986.

[4] 王小平.遗传算法-理论应用与软件实现[M].西安：西安交通大学出版社，2002.

[5] 彭满家.离心通风机整机损失计算模型的研究[D].西安：西安交通大学，1994.

[6] 樊会元.基于演化计算技术的离心压缩机静止叶栅设计方法的研究[D].西安：西安交通大学，2000.

[7] 李敏强.遗传算法的基本理论与应用[M].北京：科学出版社，2002.

[8] 任平，朱芳，赵连会. 跨音轴流压气机气动设计与数值优化[J]. 动力工程学报，2015，35(5)：373-379.

REN Ping, ZHU Fang, ZHAO Lianhui. Aerodynamic design and numerical optimization of a transonic axial flow compressor[J]. Journal of Chinese Society of Power Engineering,2015,35(5):373-379.

[9] 程航，闻苏平，徐梓轩,等.小流量系数离心式压缩机叶轮的优化设计[J].风机技术，2013(3)：44-47.

CHENG Hang,WEN Suping,XU Zixuan,etal. Optimization design of centrifugal compressor impeller with low flowrate coefficient[J].Compressor Blower & Fan Technology,2013(3):44-47.

[10] HILDEBRANDT A. Aerodynamic optimization of a centrifugal compressor return channel and u-turn with genetic algorithms[C]//ASME 2011 Turbo Expo Turbine Technical Conference Exposition. British Columbia, Canada: International Gas Turbine Institute, 2011.

[11] CHO S Y, AHN K Y, LEE Y D,etal.Optimal design of a centrifugal compressor impeller using evolutionary algorithms[J]. Mathematical Problems in Engineering,2012:752931.

[12] KIM J H, CHOI J H, HUSAIN A,etal.Multi-objective optimization of a centrifugal compressor impeller through evolutionary algorithms[J].Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy,2010,224(5):711-721.

[13] WANG X D, HIRSCH C, KANG Sh,etal.Multi-objective optimization of turbomachinery using improved NSGA-II and approximation model[J].Computer Methods in Applied Mechanics and Engineering,2011,200(9/10/11/12):883-895.

[14] MOHAN S C, MAITI D K.Structural optimization of rotating disk using response surface equation and genetic algorithm[J].International Journal for Computational Methods in Engineering Science and Mechanics,2013,14(2):124-132.

[15] 张鹏，刘波，王雷,等.高负荷吸附式压气机气动设计与分析[J].推进技术，2015，36(7)：989-995.

ZHANG Peng,LIU Bo,WANG Lei,etal. Aerodynamic design and analysis of a highly-loaded aspirated compressor[J].Journal of Propulsion Technology, 2015,36(7):989-995.

Whole Stage Optimization Design of a Centrifugal Compressor Based on Genetic Algorithm

CHENG Chao1,2, QIN Guoliang1

(1. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China;2.Xi'anShaanguPowerCo.,Ltd.,Xi'an710075,China)

A whole stage physical loss model of centrifugal compressor was founded, while a genetic algorithm procedure was programmed for optimization of the whole stage performance parameters. To verify the reliability of the physical loss model and to study the feasibility using CHC genetic algorithm to optimize the whole stage performance parameters, numerical simulations were carried out on the whole stage performance before and after optimization. Results show that compared with the performance before optimization, the whole stage performance has been improved after optimization, with more reasonable inner flow field obtained in the stage, where flow separations are avoided and flow loss is reduced.

centrifugal compressor; genetic algorithm; parameter optimization; whole stage design

2015-09-25

2015-12-30

国家重点基础研究发展计划资助项目(2012CB026000)

程 超(1980-)，男，湖北崇阳人，在职博士生，主要从事真实气体压缩机性能改进和试验方面的研究. 电话(Tel．)：13772491137；E-mail：shangu_cc@126.com．

1674-7607(2016)12-0963-07

TH452

A 学科分类号：470.30