颗粒帘换热器中颗粒空隙率的计算方法与实验研究
李 恒, 陈冬林, 程松青, 吴秀珍, 叶 托, 文 聪, 熊 颖
(1. 长沙理工大学 能源与动力工程学院, 长沙 410114;2. 株洲新时代环保科技有限公司, 湖南株洲 412007 )
颗粒帘换热器中颗粒空隙率的计算方法与实验研究
李 恒1, 陈冬林1, 程松青2, 吴秀珍2, 叶 托1, 文 聪1, 熊 颖1
(1. 长沙理工大学 能源与动力工程学院, 长沙 410114;2. 株洲新时代环保科技有限公司, 湖南株洲 412007 )
运用流动过程能量守恒原理与Ergun公式,推导出基于颗粒帘工况条件与运行参数的颗粒空隙率计算公式,并根据实验测试结果计算得到各工况条件对颗粒空隙率的影响规律.结果表明:颗粒空隙率沿下落行程呈现先减小后增大的规律;颗粒空隙率随进气速度及颗粒帘初始厚度的增大而增大,随颗粒粒径及颗粒质量流量的增大而减小;进气速度、颗粒帘初始厚度对颗粒空隙率的影响大于颗粒粒径、颗粒质量流量对颗粒空隙率的影响.
颗粒帘换热器; 颗粒空隙率; 计算公式; 实验研究
基于气固两相快速热平衡原理的颗粒帘换热器[1-5]以其系统布置灵活、换热性能卓越和换热能力实时可调等诸多优点日益受到关注.该换热器以微米级粒径的硅砂作为载热体,将烟气余热传递给载热体,再由载热体将热量传递给燃烧用空气,实现烟气余热用于预热燃烧用空气的深度回收.
颗粒空隙率是研究颗粒帘换热器中气固两相间动量传递、质量传递和热量传递的重要参数之一[6-9].但由于颗粒下落过程中具有随机性,且颗粒粒度在同一横截面上往往呈现不同的分布状态,颗粒空隙率测试困难且复杂,国内外相关研究报道较少.笔者推导了颗粒帘换热器中颗粒空隙率的数学计算公式,并通过对颗粒空隙率进行实验研究,分析了各实验工况对颗粒空隙率的影响,得到颗粒帘换热器中颗粒帘横截面平均空隙率的分布规律,为颗粒帘换热器的设计和优化操作提供依据.
1 实验装置及方法
1.1 实验装置
颗粒帘换热器冷态实验台如图1所示,该装置主要由换热单元本体、颗粒给料系统、颗粒收集系统和气体变径均流装置等组成,其中换热室通道为长×宽×高=2 000 mm×800 mm×1 000 mm的矩形通道.颗粒帘换热器中,颗粒空隙率分布实验采用3种粒径硅砂颗粒,其特性参数如表1所示.

图1 基于单级换热单元的颗粒帘换热器示意图
Fig.1 Schematic diagram of the particle curtain heat exchanger based on single-stage unit

表1 硅砂颗粒的特性参数
1.2 颗粒空隙率的计算
颗粒空隙率ε[10]定义为颗粒帘中某一横截面内颗粒间的空隙总面积(即自由截面)与整个横截面积之比,可由下式计算:
(1)
式中:qm,s为下落颗粒的质量流量,kg/s;ρs为颗粒密度,kg/m3;Vs,i为i点高度位置处颗粒帘横截面上的颗粒运动速度,m/s;Ai为i点高度位置处的颗粒帘横截面积,m2.
由于同一高度位置处颗粒帘横截面上各颗粒的运动速度难以测量或计算出来,式(1)也未考虑不同高度位置处的颗粒帘横截面颗粒浓度变化规律,因此,使用式(1)来计算颗粒空隙率时会与实际情况相差较大.
如图2所示,取某一高度位置颗粒帘横截面处的微元作为研究对象,微元长度取颗粒帘厚度Δb,宽度取换热室宽度W.定义气流与颗粒帘最后(最先)接触的颗粒帘边界线分别为颗粒帘前(后)沿,根据能量守恒原理[11-12]有:

(2)
式中:V1g为气流穿越颗粒帘前的水平速度,m/s;V2g为气流穿越颗粒帘后的水平速度,m/s;V1s为气流穿越颗粒帘前颗粒运动水平速度,m/s;V2s为气流穿越颗粒帘后颗粒运动水平速度,m/s;ρ1g为颗粒帘前部气体密度,kg/m3;ρ2g为颗粒帘后部气体密度,kg/m3;ρ1s为颗粒帘前部颗粒密度,kg/m3;ρ2s为颗粒帘后部颗粒密度,kg/m3;p1为气流穿越颗粒帘前压力,Pa;p2为气流穿越颗粒帘后压力,Pa;Δps为因颗粒存在而造成的附加压力损失,Pa;Δpg为纯气流流动时的压力损失,Pa.

(a)换热室内颗粒帘流动示意图(b)A⁃A剖面图
图2 颗粒帘微元示意图
Fig.2 Schematic diagram of the particle curtain micro-element
由于换热室内紊流运动十分强烈,可认为同一时刻同一颗粒帘横截面上的颗粒运动速度沿换热室水平方向变化很小,则可近似认为:
(3)

(4)
Δpg包括摩擦损失和气流的重力压头,可由下式[11]计算得出:
(5)
式中:fg为纯气流时的摩擦阻力因数;ρg为气体密度;Vg为气流速度;W为颗粒帘横截面当量直径,即换热室宽度;g为重力加速度.
Δps的表达式[11]为
(6)
(7)
式中:Δpsg为固体颗粒重力引起的压力损失;Δpsf为物料与壁面接触冲击和摩擦引起的压力损失;Δpss为物料颗粒彼此之间摩擦和碰撞造成的压力损失.根据文献[13]记载:
(8)
式中:fs为考虑颗粒存在时的阻力因数;qm,g为气体质量流量,kg/s.
将式(5)~式(8)代入式(4)可得:
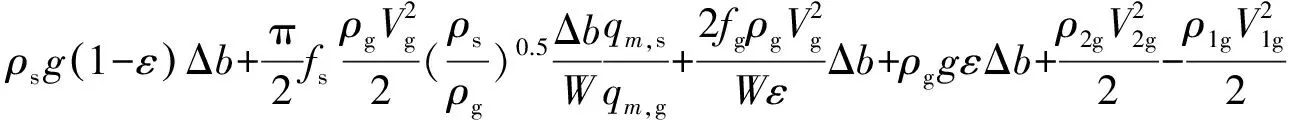
(9)
在已知实验工况条件和物料特性的情况下,由所测实验数据计算表明,物料重力引起的压降比其他各项大一个数量级以上,则可近似忽略其他各项.故气流穿越颗粒帘前后的压差Δp可简化为
(10)
利用上述公式进行计算比较复杂,影响因素较多,且实验中颗粒帘前后气流压差Δp难以准确测量.笔者试图通过建立Δp分布与颗粒空隙率分布的另一关系式,将其与式(10)联立来研究颗粒空隙率的分布.
颗粒帘换热器中气流与颗粒呈错流形式穿过颗粒帘,经计算,在本实验中换热室通道气流Re>1 000,气流穿越颗粒帘的压降可参考气流通过颗粒移动床时的压降计算方法Ergun公式[14-17]:
(11)
式中:Ф为颗粒球形度,本实验中取Ф=0.8;dm为颗粒当量直径,m;H为颗粒层高度,本实验为颗粒帘厚度Δb,m;Ure为气体与固体颗粒之间表观相对速度,m/s,可由下式[18]计算.
(12)
式中:ug为水平方向上气体实际速度,本实验中ug即为V1g;us为水平方向上颗粒实际速度,由于颗粒帘换热器中水平方向上固体颗粒之间的相互位移很小,故us可忽略不计,则可认为:
(13)
联立式(10)和式(13),得到式(14),在已知实验工况条件和物料特性的情况下测得相应实验数据,通过迭代求解即可得出各实验工况下的颗粒帘横截面颗粒空隙率ε:
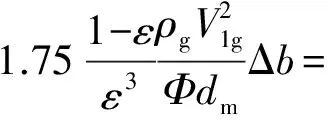
(14)
1.3 测量方法
如图3所示,在距换热室入口250 mm和出口850 mm的直线上分别设置5个直径为25 mm的测孔,各测孔间距为166 mm.各测点设置在换热室断面宽度方向的中心线上.实验时在换热室前壁的玻璃窗口粘贴透明格子薄膜,并用彩色笔记录各测点高度位置处颗粒帘前后沿边界点,测量其距离,即为此高度位置处的颗粒帘厚度.同时,为保证实验数据的准确性和可信性,使用1 076帧/s的高速数码相机对下落颗粒运动轨迹捕捉成像,将照片中处理提取出的颗粒帘厚度值与实测值加权平均即得本实验工况下的颗粒帘厚度值.实验时用热线风速仪测量并记录测点1~测点5处的气流速度,用皮托管测量并记录测点6~测点10处的气流速度(测点离测孔深度400 mm).

(a)换热室侧壁测孔示意图(b)B⁃B剖面图
图3 换热室侧壁测孔及测点布置示意图
Fig.3 Schematic diagram of measurement holes and points on side wall of the heat chamber
2 实验结果及分析
2.1 进气速度对颗粒空隙率的影响
实验中进气速度V0的调节是通过变频器调节通风机配套电机的转速来实现的,不同进气速度下的颗粒帘沿程厚度和颗粒帘后部气流速度分别如图4和图5所示,根据式(14)计算得出不同进气速度下的颗粒帘横截面颗粒空隙率(见图6),其中dp为颗粒粒径,b0为颗粒帘初始厚度.由图6可知,当进气速度由1.45 m/s增大到1.88 m/s时,颗粒空隙率也随之增大,且最大增幅出现在距换热室顶部垂直距离为166 mm处,达16.76%.其原因在于,随着进气速度的增大,颗粒与颗粒间的团聚数量减少,使得气泡通过颗粒的频率增大,气泡总体积增大,颗粒帘横截面上颗粒浓度减小,反映为颗粒帘横截面颗粒空隙率增大.

图4 不同进气速度下的颗粒帘沿程厚度
Fig.4 Curtain thickness along longitudinal direction at different inlet velocities

图5 不同进气速度下的颗粒帘后部气流速度
Fig.5 Downstream gas velocity of particle curtain at different inlet velocities
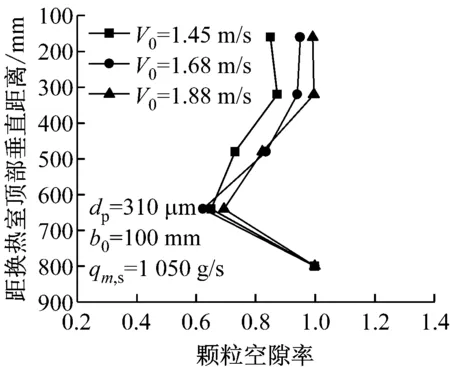
图6 不同进气速度下的颗粒空隙率
2.2 颗粒帘初始厚度对颗粒空隙率的影响
颗粒帘初始厚度b0即为颗粒刚进入换热室通道时的宽度,实验中通过改变颗粒均流装置中最下面一层筛网的有效下落宽度来改变颗粒帘初始厚度.不同颗粒帘初始厚度下的颗粒帘沿程厚度和颗粒帘后部气流速度分别如图7和图8所示,根据式(14)计算得出不同颗粒帘初始厚度下的颗粒帘横截面颗粒空隙率(见图9).由图9可知,当颗粒帘初始厚度由60 mm增大到140 mm时,颗粒帘横截面的颗粒空隙率也随之增大,且最大增幅出现在距换热室顶部垂直距离为500 mm处,达32.43%.其原因在于,在保持下落颗粒质量流量不变的情况下,随着颗粒帘初始厚度的增大,颗粒与颗粒间分布越稀疏,颗粒帘横截面上颗粒浓度减小,故颗粒帘横截面颗粒空隙率增大.

图7 不同颗粒帘初始厚度下的颗粒帘沿程厚度
Fig.7 Longitudinal thickness of particle curtain at different initial thicknesses
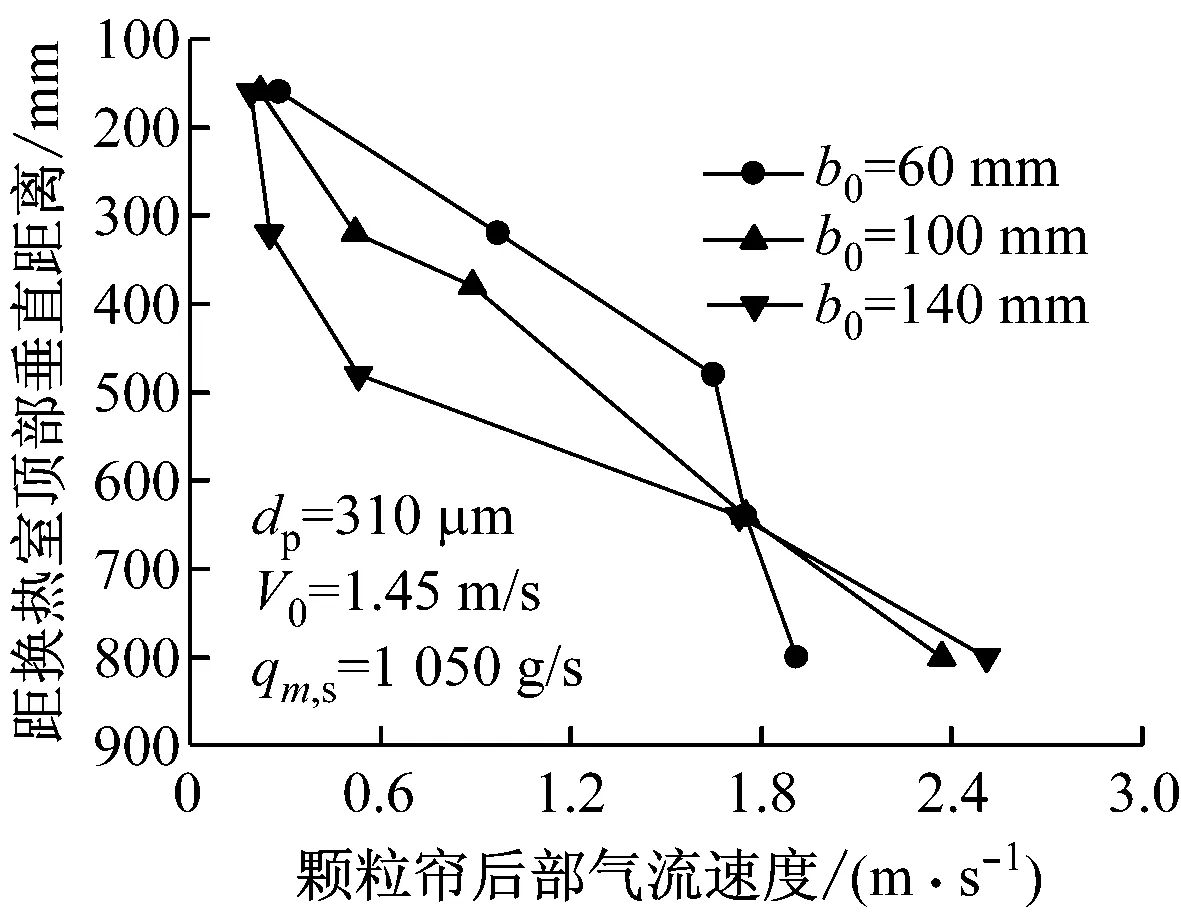
图8 不同颗粒帘初始厚度下的颗粒帘后部气流速度
Fig.8 Downstream gas velocity of particle curtain at different initial thicknesses

图9 不同颗粒帘初始厚度下的颗粒空隙率
Fig.9 Particle voidage at different initial thicknesses of particle curtain
2.3 颗粒粒径对颗粒空隙率的影响
实验中不同颗粒粒径(取颗粒平均粒径)dp的硅砂颗粒通过不同孔径的筛网来分级获得.不同颗粒粒径下的颗粒帘沿程厚度和颗粒帘后部气流速度分别如图10和图11所示,根据式(14)计算得出不同颗粒粒径下的颗粒帘横截面颗粒空隙率(见图12).由图12可知,当颗粒粒径dp由215 μm增大到310 μm时,颗粒空隙率呈减小趋势,且最大减幅出现在距换热室顶部垂直距离为500 mm处,达13.9%.其原因在于,当颗粒粒径增大时,颗粒比表面积随之减小,使得气固两相相互作用的面积减小,两相间动量交换程度减弱,颗粒水平方向速度分量减小,颗粒帘横截面上颗粒浓度增大,表现为颗粒帘横截面颗粒空隙率减小.

图10 不同颗粒粒径下的颗粒帘沿程厚度
Fig.10 Longitudinal thickness of particle curtain at different particle sizes
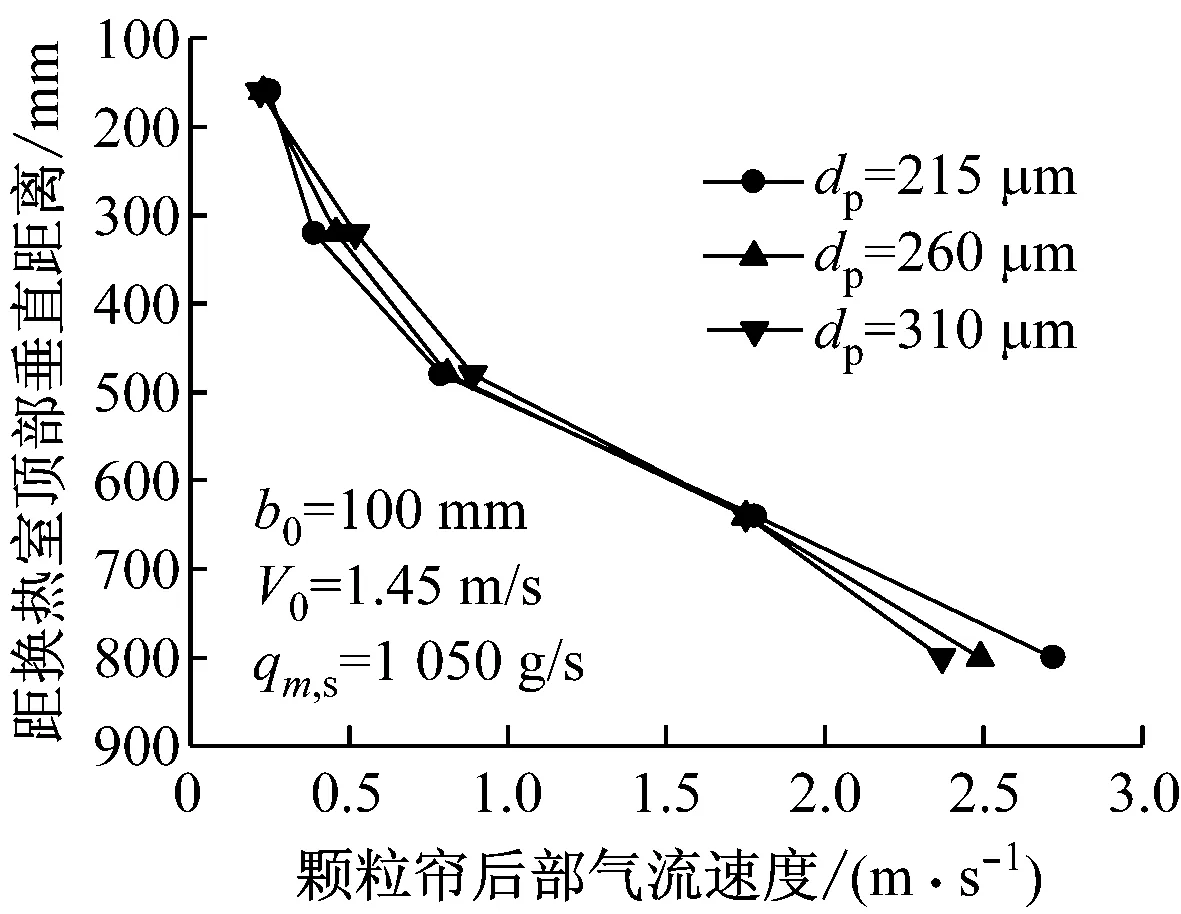
图11 不同颗粒粒径下的颗粒帘后部气流速度
Fig.11 Downstream gas velocity of particle curtain at different particle sizes
2.4 颗粒质量流量对颗粒空隙率的影响
颗粒质量流量qm,s的调节是通过控制位于给料料罐和颗粒均流装置之间的放料蝶阀开度来实现的.不同颗粒质量流量下的颗粒帘沿程厚度和颗粒帘后部气流速度分别如图13和图14所示,根据式(14)计算得出不同颗粒质量流量下的颗粒帘横截面颗粒空隙率(见图15).由图15可知,当颗粒质量流量qm,s由550 g/s增大到1 650 g/s时,颗粒空隙率呈减小趋势,且最大减幅出现在距换热室顶部垂直距离为666 mm处,达7.61%.其原因在于,在保持颗粒帘初始厚度不变且颗粒沿下落截面分布均匀的情况下,随着颗粒质量流量的增大,下落颗粒帘横截面上颗粒数量越多且颗粒帘中颗粒之间的致密程度也增加,表现为颗粒帘横截面平均空隙率减小.
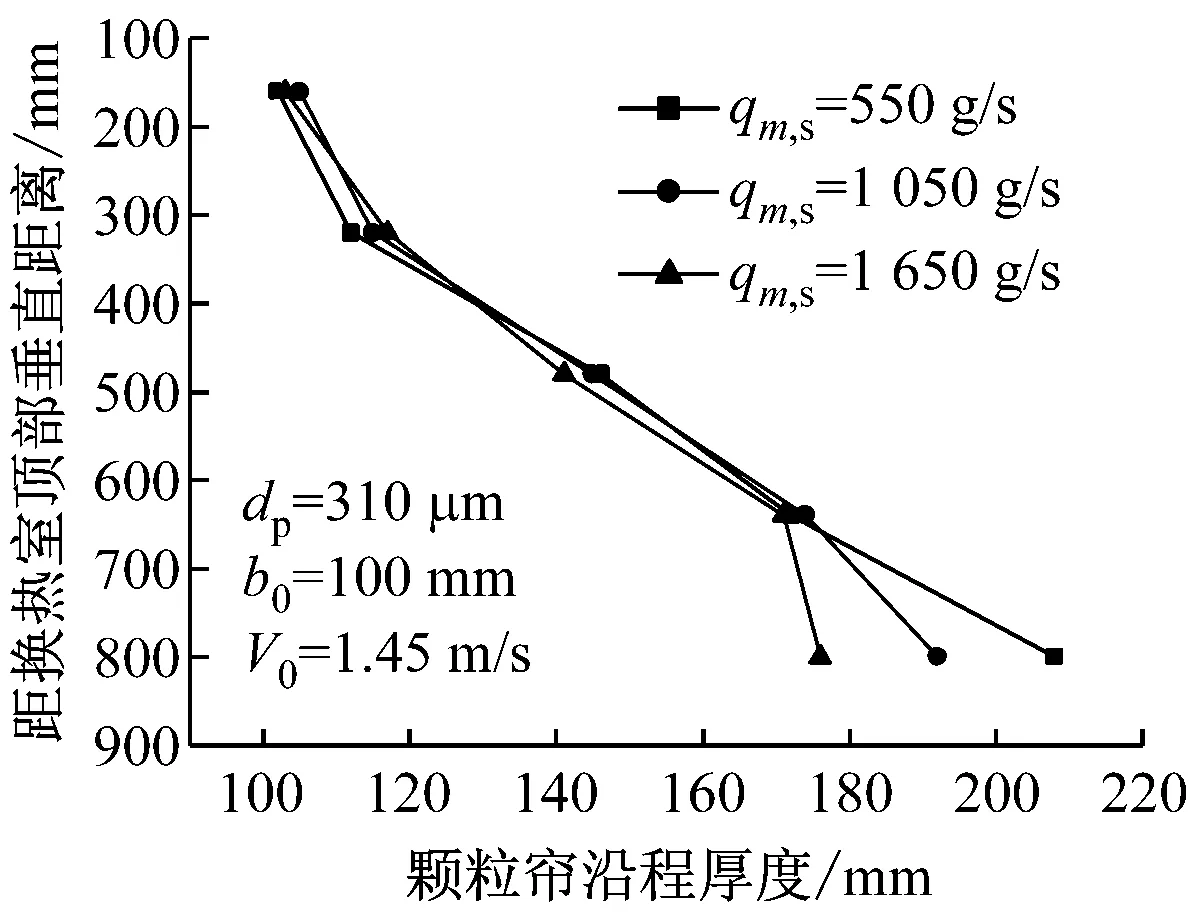
图13 不同颗粒质量流量下的颗粒帘沿程厚度
Fig.13 Longitudinal thickness of particle curtain at different mass flow rates of particles

图14 不同颗粒质量流量下的颗粒帘后部气流速度
Fig.14 Downstream gas velocity of particle curtain at different mass flow rates of particles
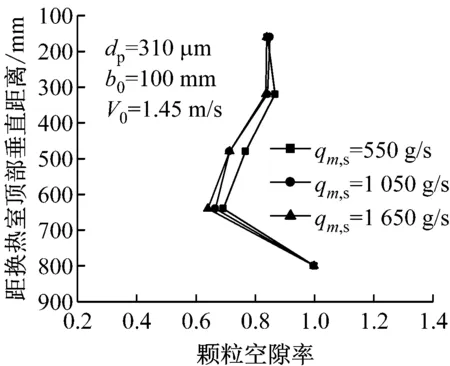
图15 不同颗粒质量流量下的颗粒空隙率
由图6、图9、图12和图15可知,各实验工况下的颗粒帘横截面颗粒空隙率随颗粒帘下落高度的增加先减小后增大,越接近换热室底部,颗粒帘横截面颗粒空隙率越大.这是因为颗粒在下落过程中综合运动速度的逐渐增大使得颗粒帘横截面上颗粒浓度逐渐增大,尽管颗粒帘下落过程中颗粒帘沿程厚度在逐渐增大,但颗粒帘下落初期颗粒帘沿程厚度增加较缓慢,此时颗粒浓度的增幅超出颗粒帘沿程厚度的增幅,因此颗粒帘横截面颗粒空隙率逐渐减小;当颗粒帘下落至某一高度位置处(距换热室顶部约650 mm)时颗粒帘横截面的颗粒空隙率减小至最小值,此后颗粒帘沿程厚度的增幅大大超出颗粒浓度的增幅,因而颗粒空隙率又快速增大.
3 结 论
(1) 在一定的操作条件下,颗粒帘换热器中颗粒空隙率随进气速度及颗粒帘初始厚度的增大而增大,随颗粒粒径及颗粒质量流量的增大而减小.
(2) 随着下落高度的增加,颗粒空隙率先减小后增大.
(3) 进气速度、颗粒帘初始厚度对颗粒空隙率的影响大于颗粒粒径、颗粒质量流量对颗粒空隙率的影响.
[1] 陈冬林, 秦小林.无管换热器: 201120261405.2[P]. 2011-07-22.
[2] 陈冬林, 秦小林. 无管换热器及余热回收系统: 201110206635.3[P]. 2011-07-22.
[3] 陈冬林, 邹婵, 杜洋, 等. 颗粒帘换热单元的稳态换热特性研究[J]. 热力发电, 2014, 43(3): 37-42.
CHEN Donglin, ZOU Chan, DU Yang,etal. Steady heat transfer characteristics of a particle curtain based heat exchanger[J]. Thermal Power Generation, 2014, 43(3): 37-42.
[4] 陈冬林, 王甘泉, 王安. 颗粒帘换热器颗粒均流装置的设计与实验[J]. 电力科学与技术学报, 2014, 29(1): 75-79.
CHEN Donglin, WANG Ganquan, WANG An. Design and experimental investigation of the uniforming device of particles from particle curtain heat exchanger[J]. Journal of Electric Power Science and Technology, 2014, 29(1): 75-79.
[5] 陈冬林, 杨建波, 程松青, 等. 颗粒帘换热器中气体变径均流装置的设计与实验研究[J]. 电力科学与技术学报, 2015, 30(1): 93-98.
CHEN Donglin, YANG Jianbo, CHENG Songqing,etal. Design and experimental investigation in the airflow uniform device for particle curtain heat exchangers[J]. Journal of Electric Power Science and Technology, 2015, 30(1): 93-98.
[6] ANDALIB M, ZHU J, NAKHLA G. A new definition of bed expansion index and voidage for fluidized biofilm-coated particles[J]. Chemical Engineering Journal, 2012, 189-190: 244-249.
[7] ANAND A, CURTIS J S, WASSGREN C R,etal. Predicting discharge dynamics from a rectangular hopper using the discrete element method (DEM)[J]. Chemical Engineering Science, 2008, 63(24): 5821-5830.
[8] ZHANG Huili, DEGRVE J, BAEYENS J,etal. The voidage in a CFB riser as function of solids flux and gas velocity[C]//New Paradigm of Particle Science and Technology Proceedings of the 7th World Congress on Particle Technology. Beijing, China: Elsevier, 2015.
[9] 陶贺, 金保昇, 钟文琪. 不同物性对椭球形颗粒在移动床中流动特性影响的模拟研究[J]. 中国电机工程学报, 2011, 31(5): 68-75.
TAO He, JIN Baosheng, ZHONG Wenqi. Effect of particle properties on the flow behaviors of ellipsoidal particles in the moving bed[J]. Proceedings of the CSEE, 2011, 31(5): 68-75.
[10] 张朋刚, 董辉. 散料层的空隙率检测方法[J]. 材料与冶金学报, 2012, 11(2): 146-151, 156.
ZHANG Penggang, DONG Hui. Measurement of void fraction in packed beds[J]. Journal of Materials and Metallurgy, 2012, 11(2): 146-151, 156.
[11] 骆仲泱, 岑可法, 倪明江. 循环流化床流体动力特性的试验研究[J]. 浙江大学学报(自然科学版), 1987, 21(6): 84-92.
LUO Zhongyang, CEN Kefa, NI Mingjiang. Experimental research on hydrodynamical properties of circulating fluidized bed[J]. Journal of Zhejiang University (Natural Science), 1987, 21(6): 84-92.
[12] CEN Kefa, LUO Zhongyang. Experimental research on hydrodynamical properties of circulating fluidized bed[C]//Proceedings of 9th International Conference on Fluidized Bed Combustion. Hangzhou: Journal of Zhejiang University: 1987: 529-533.
[13] KUNII D, LEVENSPIEL O, BRENNER H. Fluidization engineering[M]. 2nd ed. Boston, USA: Butterworth-Heinemann, 1991.
[14] 王奎升. 工程流体与粉体力学基础[M]. 北京: 中国计量出版社, 2002.
[15] 龙文宇, 范怡平, 卢春喜, 等. 气固错流移动床内空腔与贴壁研究现状及发展[J]. 应用化工, 2015, 44(11): 2091-2096.
LONG Wenyu, FAN Yiping, LU Chunxi,etal. An overview of cavity and pinning in cross-flow moving beds[J]. Applied Chemical Industry, 2015, 44(11): 2091-2096.
[16] 向杰, 李清海, 张衍国, 等. 卧式循环流化床锅炉压降和颗粒体积分数分布[J]. 动力工程学报, 2014, 34(4): 253-259, 266.
XIANG Jie, LI Qinghai, ZHANG Yanguo,etal. Distribution of pressure drop and particle concentration in a horizontal circulating fluidized bed boiler[J]. Journal of Chinese Society of Power Engineering, 2014, 34(4): 253-259, 266.
[17] MAYERHOFER M, GOVAERTS J, PARMENTIER N,etal. Experimental investigation of pressure drop in packed beds of irregular shaped wood particles[J]. Power Technology, 2011, 205(1/2/3): 30-35.
[18] 郜时旺. 移动床颗粒层过滤系统高温高压除尘研究[D]. 西安: 西安交通大学, 2002: 73-74.
Calculation Method and Experimental Study of Particle Voidage in Particle Curtain Heat Exchanger
LI Heng1, CHEN Donglin1, CHENG Songqing2, WU Xiuzhen2,YETuo1,WENCong1,XIONGYing1
(1.School of Energy and Power Engineering, Changsha University of Science and Technology,Changsha 410114, China; 2. Zhuzhou New Times Environmental Protection Technology Co., Ltd.,Zhuzhou 412007, Hunan Province, China)
A calculation formula of particle voidage was deduced using energy conservation principle and Ergun formula based on particle curtain working conditions and operation parameters, while the effects of various working conditions on the voidage were studied according to the experimental data of a particle curtain heat exchanger. Results show that the voidage in particle curtain first decreases and then increases along the descending direction, which increases with rising inlet velocity and initial curtain thickness, and with reducing particle size and mass flow rate. Both the inlet gas velocity and initial curtain thickness affects more on the voidage than the particle size and mass flow rate.
particle curtain heat exchanger; partical voidage; calculation formula; experimental study
2015-12-11
2016-03-26
湖南省科技计划资助项目(2013KG3193);湖南省教育厅科学研究基金重点资助项目(10A004)
李 恒(1991-),男,江西萍乡人,硕士研究生,主要从事节能原理与技术方面的研究. 陈冬林(通信作者),男,教授,博士生导师,电话(Tel.):13974837965;E-mail:chendl_01@sina.com.
1674-7607(2016)12-0970-06
TK172
A 学科分类号:470.20

