基于高斯过程回归的燃煤烟气汞排放预测

钟 美， 赵兵涛， 黄 朔

(上海理工大学 能源与动力工程学院，上海 200093)



基于高斯过程回归的燃煤烟气汞排放预测

钟 美， 赵兵涛， 黄 朔

(上海理工大学 能源与动力工程学院，上海 200093)

选取对烟气汞排放影响显著的特征参数，采用一类新的随机过程方法——高斯过程回归模型来预测烟气中单质汞、氧化汞和颗粒汞的排放浓度,分别讨论了协方差函数和样本比例对模拟预测精度的统计学影响.结果表明:平方指数协方差函数优于有理二次协方差函数和Matern协方差函数；预测精度随样本比例的增大而提高；高斯过程回归模型优于常规非线性模化方法并显示出更好的鲁棒性，对烟气中汞的形态预测有较好的适用性.

燃煤烟气； 汞形态； 高斯过程回归； 模化； 预测

化石燃料燃烧特别是煤燃烧过程中生成的污染物已经成为一类重要的能源与环境问题.除SO2、NOx和CO2以外，汞的排放以其剧毒性、累积性和持久性越来越受到重视[1-3].燃煤烟气中汞通常有3种形态：单质汞(Hg0)、氧化汞(Hg2+)和颗粒汞(Hgp).不同形态的汞之间可以相互转化，且煤的特性(如煤的热值，煤中Hg、Cl、S的含量等)和操作条件(如炉膛的温度和压力)等众多因素对汞的形态都会产生影响.

为了有效预测燃煤烟气汞排放的形态与浓度，近十年来已发展出相关的理论和方法，如神经网络(ANN)、基于组的数据处理诱导神经网络法(GMDH-ANN)、支持向量机(SVM)和贝叶斯正则化人工神经网络(BRANN).但是这些方法本身仍存在问题，如神经网络法存在最优网络结构(隐层神经元个数)难以确定和过拟合的问题；SVM的核函数的最优化参数需要经过优化算法耦合，以交叉验证的复杂过程确定.同时，上述方法的结果大多是孤立、单次的预测结果，缺乏实际统计学指导意义.

高斯过程回归(GPR)是近年来发展的一种新型贝叶斯非参数模型[4-5]，它是一种定义在无限维参数空间上的贝叶斯模型，可以很好地自适应接收到数据.笔者应用该方法对燃煤过程中不同形态的汞排放浓度进行模化和预测，以期对其评估和控制提供有效方法和手段.

1 高斯过程回归模型的基本原理

在高斯过程回归模型中，给定训练集D={(xi,yi)|i=1,2,…,n}，其中xi、yi分别表示D中的第i个输入和输出向量.高斯过程回归模型对输入向量与目标输出之间的关系f进行推断，即给定输入向量时确定目标输出的条件分布[6].

假定f是一个以m为均值函数、k为协方差函数的高斯过程，即f～GP(m，k).高斯过程是一个随机过程，可由其均值函数与协方差函数完全确定[7].

根据高斯过程的定义可知，f(x1)，f(x2)，…，f(xn)服从多元高斯分布，且该多元高斯分布的均值向量为m(xi)，协方差矩阵为K，因此

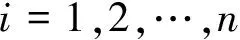
(1)

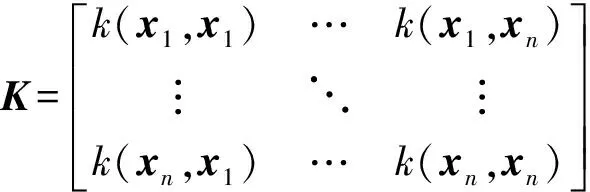
实际中的目标输出通常会包含一些噪声：y=f(x)+ε，其中ε～N(0,σn2).

于是问题转换为已经观测到训练集D：yi=f(xi)+εi(i=1，2，…，n)，需要在测试集D*={(xi*,yi*)|i=n+1,n+2,…,n+n*}预测对应的输出值f*.设置高斯过程的均值函数为零常函数，训练集的输出向量y和测试集的预测值f*的多元高斯分布为

(2)

其中，K*=[k(x*,x1),k(x*,x2),…,k(x*,xn)],K**=k(x*,x*).

式中：σn为噪声的标准差.

根据多元高斯分布的条件分布形式，可得出高斯过程回归模型预测方程的关键：

(3)

式中：矩阵X由训练集的输入xi的列向量组成；矩阵X*由测试集的输入xi*的列向量组成.

(4)

(5)

协方差函数对于高斯过程至关重要，在高斯过程回归模型中协方差函数(即核函数)必须满足Mercer条件.采用了3种协方差函数：

平方指数协方差(SE)函数：

(6)

有理二次协方差(RQ)函数：

(7)

Matern协方差(Matern)函数

(8)

式中：σf2为核函数的信号方差;M=diag(l-2)；l为关联性测定超参数；δij为克洛内克尔符号，i和j相同时为1，不同时为0，其值越大，说明输入与输出的相关性越小，表示控制局部相关性的程度；α为核函数的形状参数；j=1,2，…，n.

令超参数θ=(l，σf，σn)，可通过极大似然法自适应获得最优解.首先建立训练样本条件概率的负对数似然函数，并令其对超参数求偏导，然后采用共轭梯度法对该偏导数进行最小化，以得到超参数的最优解.

2 基于GPR的汞排放浓度预测的模化方法与过程

2.1 变量参数与数据样本

影响烟气中各种形态汞排放浓度的因素较多，选取6个较为显著的影响因素来分析其对烟气中汞排放浓度的影响.

研究表明，在温度高于400 K的还原性气氛及温度高于600 K的氧化性气氛的烟气中，99%以上的汞以单质汞的形态存在[8].分析S对汞形态的影响，结果表明，在燃烧产生的氧化性气氛烟气中，随着烟气温度的降低，单质汞将发生化学反应生成氧化汞，S的存在可以促进汞元素以固相硫酸汞的形式沉积下来[9].Cl对汞形态的影响在氧化性气氛中表现为，烟气中Cl的含量越大，生成稳定相氯化汞的温度范围越宽[8].烟气中单质汞的浓度基本随着煤中Cl含量的增加而降低[10].汞吸附量随飞灰烧失量的增加而增加.飞灰中不同类型介质的气相汞吸附特性差异显著，其中未燃尽碳吸附性能最强，吸附剂的比表面积与其汞吸附量呈正相关关系.燃煤飞灰碳粒所具有的多孔隙结构和巨大比表面积有利于吸附、脱除烟气中的汞，使得烟气中氧化汞和单质汞含量降低[11].烟气中的NOx与飞灰相互作用还可以催化氧化单质汞[12].煤中的汞可以在150 ℃左右的低温下挥发，在炉膛内燃烧温度下，汞将蒸发并以单质汞的形态存在于气相中，随着烟气温度降低，单质汞会与烟气中的其他成分发生一系列化学反应，最终大部分汞将以单质态随烟气排放到环境中[13].汞元素和氯元素都是煤中最易挥发的元素，它们在煤热解过程中迅速蒸发，然后在气相中相互反应[10].煤的部分发热量可间接地反映在锅炉负荷上，随着锅炉负荷的降低，烟气中汞的排放总量降低，烟气中汞的浓度略有下降[14].

基于上述分析，选取煤的发热量，煤中Hg含量、Cl含量和S含量，以及灰分和温度作为GPR的输入变量，3种形态的汞浓度作为输出变量.数据库共计82组数据，均来源于文献[15].高斯过程回归模型模拟预测分为2个步骤，首先确定训练样本和测试样本，再以训练样本对高斯过程回归模型进行训练，以测试样本进行验证，最后评估其模拟和泛化性能.

2.2 归一化处理

不同评价指标往往具有不同的量级和单位，会影响到数据分析的结果.为消除数据指标之间的量级影响和解决其不可比性的问题，对数据进行归一化处理.将所有数据转化成处于同一数量级的无量纲数，且全部落在0～1，以进行综合对比评价.最后，对模拟结果进行反归一化处理，得到具有量纲单位的汞形态浓度作为输出.

2.3 评价指标

采用均方误差(E2)和确定系数(R2)对预测结果和模型进行评价.

(9)

(10)

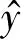
为了避免单次模拟结果的随机性影响，采用上述指标的10次均值统计结果进行评估.

3 结果与讨论

3.1 协方差函数的影响

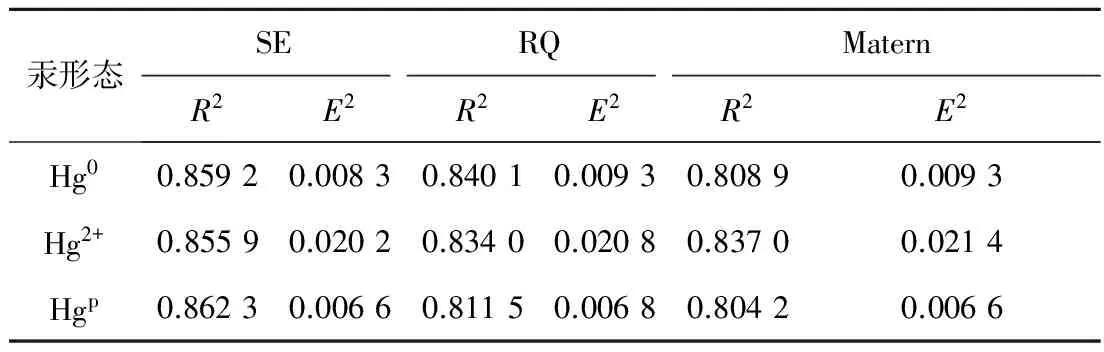
为了比较不同协方差函数对高斯过程回归模型模拟结果的影响，固定训练样本和测试样本比例为85%∶15%，即训练组为70组数据，测试组为12组数据，采用3种协方差函数进行了10次随机模拟，测试组统计结果见表1.

表1 不同协方差函数随机10次预测结果的统计值

Tab.1 Statistics of random 10 times of prediction results by different covariance functions

汞形态SERQMaternR2E2R2E2R2E2Hg00．85920．00830．84010．00930．80890．0093Hg2+0．85590．02020．83400．02080．83700．0214Hgp0．86230．00660．81150．00680．80420．0066

从预测结果可以看出采用不同核函数时测试样本的预测精度不同.对测试样本预测精度的比较表明，SE核函数具有更好的性能.尽管对于训练样本而言，3个核函数均可达到较高的预测精度，SE的R2为0.94～0.96，RQ的R2为0.94～0.97，Matern的R2为0.98～1，三者的R2≥0.94.基于Matern核函数的模型可以达到近似1的确定系数以及近似0的误差精度，但这同时可能导致过拟合现象.由于测试样本的预测精度更能反映模型本身的鲁棒性和泛化性能，因此最优协方差函数为SE.

3.2 样本比例的影响

为比较不同训练样本与测试样本的比例对汞排放浓度预测结果的影响，现固定SE为优化选择的协方差函数，分别比较训练样本与测试样本比例为80%∶20% (66组和16组)、85%∶15%(70组和12组)及90%∶10%(74组和8组)时10次随机预测结果的统计值，测试组结果见表2.

总体上，预测精度随样本比例的增大而提高，尽管样本比例对训练样本的预测精度影响不大，R2为0.93～0.97，但是随着样本比例的增大，测试样本的预测精度有所提高.这与模型获得的学习信息的健全度有关，对于汞排放浓度数据挖掘的深度和广度有助于模型泛化性能的提高.

3.3 与其他模型的比较

为了表征最优化的GPR预测性能，图1～图3给出了以85%∶15%作为训练组和测试组的样本比例，平方指数协方差(SE)函数作为核函数，在对单质汞(Hg0)、氧化汞(Hg2+)和颗粒汞(Hgp)的10次随机预测结果中最优的模拟结果.对于单质汞和颗粒汞，测试组的均方误差(MSE)均比训练组小.就确定系数而言，训练组的确定系数(0.926～0.954)远小于测试组的确定系数(0.957～0.986)，说明对于未知的数据，高斯过程回归模型具有良好的预测性能，并且可以得出比训练组更准确的预测结果.

表2 不同样本比例时10次随机预测结果的统计值

Tab.2 Statistics of random 10 times of prediction results for different sample ratios

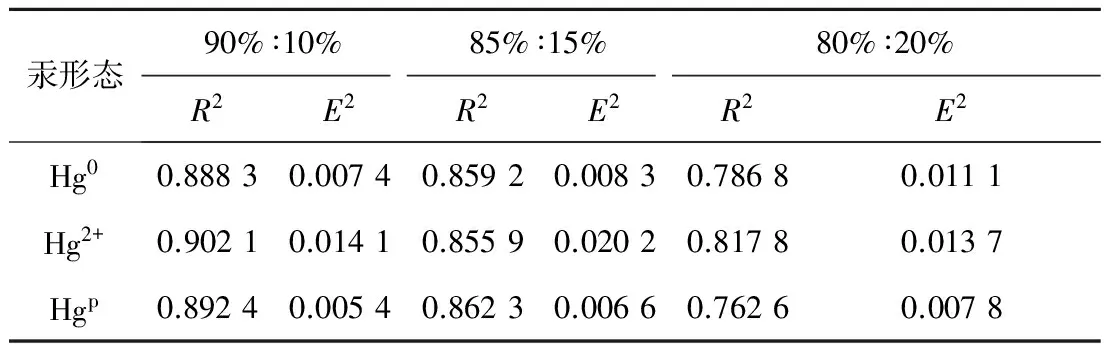
汞形态90%∶10%85%∶15%80%∶20%R2E2R2E2R2E2Hg00．88830．00740．85920．00830．78680．0111Hg2+0．90210．01410．85590．02020．81780．0137Hgp0．89240．00540．86230．00660．76260．0078

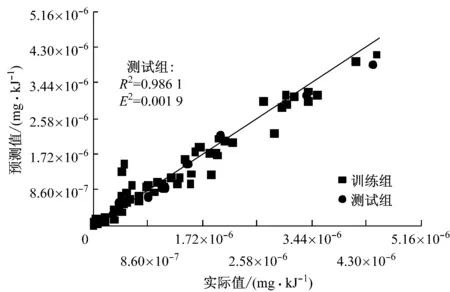
图1 对单质汞的模拟结果

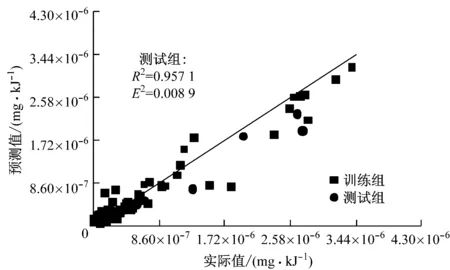
图2 对氧化汞的模拟结果

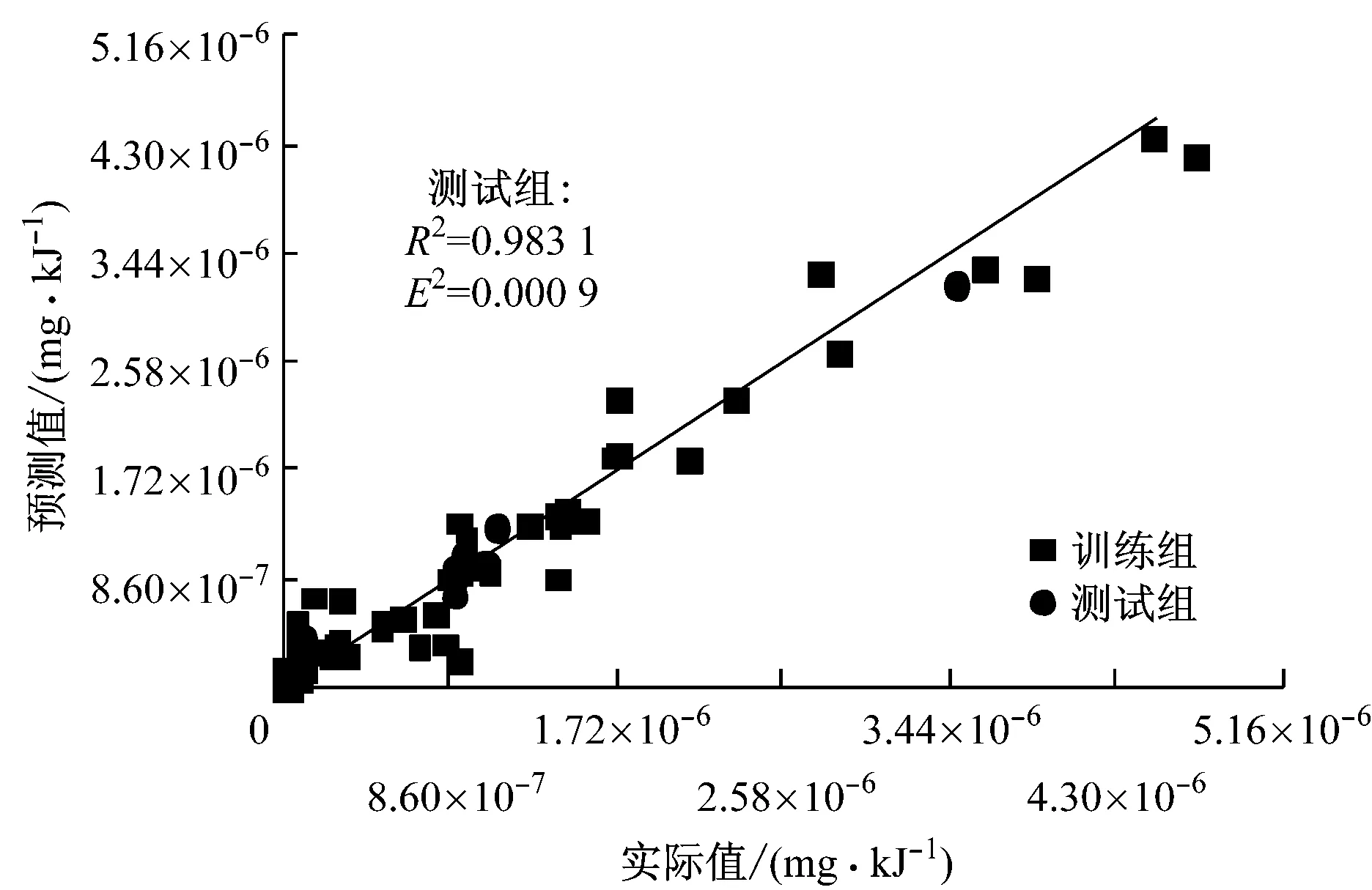
图3 对颗粒汞的模拟结果

表3给出了不同模型对烟气中汞形态预测的模拟结果，所有模型模拟数据均来源于参考文献[15].

表3 烟气汞形态预测的其他方法

Tab.3 Other methods for prediction of mercury speciation in coal-fired flue gas

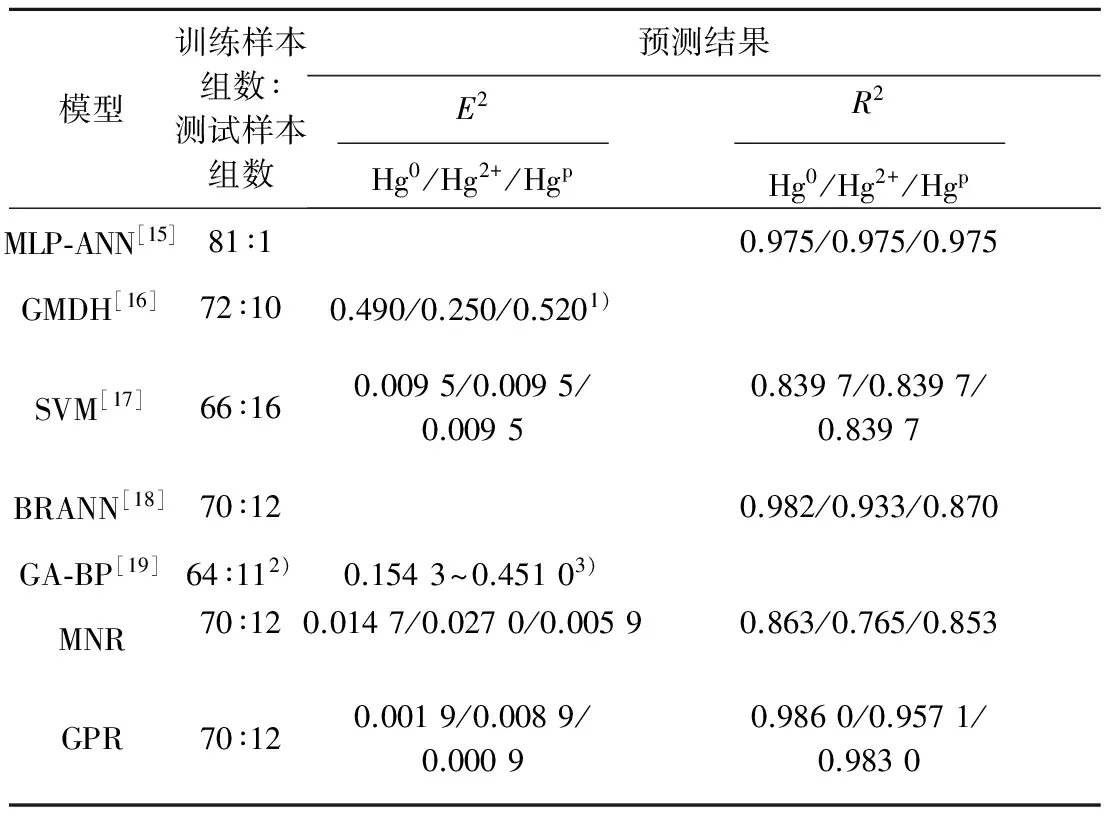
模型训练样本组数∶测试样本组数预测结果E2 Hg0/Hg2+/Hgp R2 Hg0/Hg2+/Hgp MLP⁃ANN[15]81∶10．975/0．975/0．975GMDH[16]72∶100．490/0．250/0．5201)SVM[17]66∶160．0095/0．0095/0．00950．8397/0．8397/0．8397BRANN[18]70∶120．982/0．933/0．870GA⁃BP[19]64∶112)0．1543～0．45103)MNR70∶120．0147/0．0270/0．00590．863/0．765/0．853GPR70∶120．0019/0．0089/0．00090．9860/0．9571/0．9830

注：1)绝对平均误差(MAE)；2)选取了82组中的75组；3)向量误差.

Jensen等[15]使用多层感知器-人工神经网络(MLP-ANN)对烟气中汞的形态进行模拟.MLP-ANN具有3层网络结构：输入层、隐藏层和输出层.优化结果表明，隐藏层的节点数为8时具有最好的性能.MLP-ANN的结构通过反向传播进行训练，以优化权重集使得预测值与实际值间的误差最小为目的.其对预测值的确定系数为0.975，虽然结果较好，但只取一组数据并不能全面表征网络的泛化性能，并且神经网络自身存在隐藏层神经元个数难以确定和过拟合的问题.

基于组的数据处理算法(GMDH)的诱导网络[16]与神经网络相比，可以更快建立模型，且很少或不需要用户的干预，模型收敛更快，不陷于局部最小值，可自动选择有效的输入变量、自动配置模型的结构.GMDH对训练组的模拟结果确定系数为0.945/0.884/0.869(Hg0/Hg2+/Hgp).虽然2种方法采取的样本容量稍有不同(GMDH训练组为72组)，且GMDH在研究输入对输出的影响权重方面有很好的指示性，但其预测性能不如高斯过程回归模型.

支持向量机(SVM)[17]是一种基于核函数的学习机器，其泛化能力在很大程度上依赖于所选择的核函数.且SVM核函数的选定及其最优化参数需要通过优化算法与交叉验证的方法确定.SVM在核函数参数寻优过程中花费的中央处理器(CPU)时间成本高于高斯过程回归模型.从模拟结果来看，SVM对训练组的拟合程度很高，确定系数为0.979 5，高于本文中的高斯过程回归模型，但对于测试组而言，确定系数仅为0.839 7，远低于高斯过程回归模型的预测结果.比较训练组与测试组的确定系数可以看出，SVM较容易出现过拟合，对未知数据的预测性能较高斯过程回归模型差.

贝叶斯正则化人工神经网络(BRANN)[18]使用的是3层前馈网络，输入层、隐藏层和输出层节点数分别为6、12和3.通过各层之间的连接权重和偏差值对输入进行转化，最后得到输出值.模拟结果表明，虽然训练组的确定系数0.956/0.951/0.962(Hg0/Hg2+/Hgp)较高，但是对于测试组的确定系数，高斯过程回归模型优于贝叶斯正则化人工神经网络模型.可见贝叶斯正则化人工神经网络模型测试组的预测结果准确性低于训练组模拟结果的准确性，而高斯过程回归模型模拟结果则表明测试组预测结果的准确性可以远高于训练组，这说明高斯过程回归模型对未知数据的泛化性能远优于贝叶斯正则化人工神经网络模型.

为进一步比较高斯过程回归模型与传统的多元非线性回归(MNR)模型的预测精度，表3给出了其比较结果.由表3可以看出，高斯过程回归模型的模拟结果远优于多元非线性回归模型，表明变量对汞排放的影响不是简单的指数关系.此外，多元非线性回归模型需要预先定义经验模型，而高斯过程回归模型只需要提供训练组数据就可以对模型进行训练，且多元非线性回归模型不适用于复杂、高度非线性数据的拟合.

4 结 论

(1)高斯过程回归模型自适应性强，与神经网络和支持向量机相比,具有容易实现、超参数自适应获取等优点.将其应用于燃煤烟气中不同形态汞排放浓度的预测是可行的.由于燃烧过程中汞形态和浓度的影响因素众多，在自变量的选取上没有考虑飞灰的理化特性和锅炉负荷等因素的影响，后续将会对此进行研究.此外，由于数据样本规模的限制，仅对82组数据进行了模拟，如有更多数据样本，可进一步提高模型的准确性和可靠性.

(2)随机模拟的统计学性能表明，核函数的选取对高斯过程回归模型的结果产生影响.平方指数协方差函数作为核函数时，其泛化性能优于有理二次协方差函数和Matern协方差函数.

(3)训练样本与测试样本的比例发生变化时，预测结果也随之发生变化.预测结果的统计学精度随训练样本与测试样本比例的增大而提高.

(4)与已有的预测模型和传统多元非线性回归模型相比，GPR具有较高的预测精度和泛化性能.

[1] LI P, FENG X B, QIU G L,etal. Mercury pollution in Asia: a review of the contaminated sites[J]. Journal of Hazardous Materials, 2009, 168(2/3): 591-601.

[2] GRAYDON J W, ZHANG X, KIRK D W,etal. Sorption and stability of mercury on activated carbon for emission control[J]. Journal of Hazardous Materials, 2009, 168(2/3): 978-982.

[3] 杨建平, 赵永椿, 张军营, 等. 燃煤电站飞灰对汞的氧化和捕获的研究进展[J]. 动力工程学报, 2014, 34(5): 337-345.

YANG Jianping, ZHAO Yongchun, ZHANG Junying,etal. Research process on mercury oxidation and capture with fly ash of coal-fired power plant[J]. Journal of Chinese Society of Power Engineering, 2014, 34(5): 337-345.

[4] RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. Cambridge, Massachusetts USA: MIT Press, 2006.

[5] KOTTAS A, BEHSETA S, MOORMAN D E,etal. Bayesian nonparametric analysis of neuronal intensity rates[J]. Journal of Neuroscience Methods, 2012, 203(1): 241-253.

[6] 何志昆, 刘光斌, 赵曦晶, 等. 高斯过程回归方法综述[J]. 控制与决策, 2013, 28(8): 1121-1129, 1137.

HE Zhikun, LIU Guangbin, ZHAO Xijing,etal. Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121-1129, 1137.

[7] PARK C, HUANG J Z, DING Y. Domain decomposition approach for fast Gaussian process regression of large spatial data sets[J]. The Journal of Machine Learning Research, 2011, 12(4): 1697-1728.

[8] 刘迎晖, 郑楚光, 游小清, 等. 氯元素对烟气中汞的形态和分布的影响[J]. 环境科学学报, 2001, 21(1): 69-73.

LIU Yinghui, ZHENG Chuguang, YOU Xiaoqing,etal. Effect of chlorine on the speciation of mercury in flue gases[J]. Acta Scientiae Circumstantiae, 2001, 21(1): 69-73.

[9] 王泉海, 邱建荣, 吴昊. 硫元素对烟气中汞的形态和分布的影响[J]. 燃烧科学与技术, 2003, 9(2): 135-138.

WANG Quanhai, QIU Jianrong, WU Hao. Effect of sulfur on the speciation of mercury in flue gases[J]. Journal of Combustion Science and Technology, 2003, 9(2): 135-138.

[10] CAO Yan, DUAN Yufeng, KELLIE S,etal. Impact of coal chlorine on mercury speciation and emission from a 100 MW utility boiler with cold-side electrostatic precipitators and low-NOxburners[J]. Energy & Fuels, 2005, 19(3): 842-854.

[11] 彭苏萍, 王立刚. 燃煤飞灰对锅炉烟道气汞的吸附研究[J]. 煤炭科学技术, 2002, 30(9): 33-35.

PENG Suping, WANG Ligang. Study on Hg adsorption of flying ash in flue gas[J]. Coal Science and Technology, 2002, 30(9): 33-35.

[12] LAUDAL D L, BROWN T D, NOTT B R. Effects of flue gas constituents on mercury speciation[J]. Fuel Processing Technology, 2000(65/66): 157-165.

[13] 杨祥花, 江贻满, 杨立国, 等. 燃煤汞形态分布和排放特性研究[J]. 洁净煤燃烧与发电技术, 2006(1): 13-16.

YANG Xianghua, JIANG Yiman, YANG Liguo,etal. Research summary on phase distribution and emission characteristics of Hg of burned-coal[J]. Energy Research & Utilization, 2006(1): 13-16.

[14] 朱珍锦, 薛来, 谈仪, 等. 负荷改变对煤粉锅炉燃烧产物中汞的分布特征影响研究[J]. 中国电机工程学报, 2001, 21(7): 87-90, 94.

ZHU Zhenjin, XUE Lai, TAN Yi,etal. Studies on characteristics of mercury distribution in combustion products at various loads of A P. C.-fired utility boiler[J]. Proceedings of the CSEE, 2001, 21(7): 87-90, 94.

[15] JENSEN R R, KARKI S, SALEHFAR H. Artificial neural network-based estimation of mercury speciation in combustion flue gases[J]. Fuel Processing Technology, 2004, 85(6/7): 451-462.

[16] ABDEL-AAL R E. Predictive modeling of mercury speciation in combustion flue gases using GMDH-based abductive networks[J]. Fuel Processing Technology, 2007, 88(5): 483-491.

[17] ZHAO Bingtao, ZHANG Zhongxiao, JIN Jing,etal. Modeling mercury speciation in combustion flue gases using support vector machine: prediction and evaluation[J]. Journal of Hazardous Materials, 2010, 174(1/3): 244-250.

[18] TICKNOR J L, HSU-KIM H, DESHUSSES M A. A robust framework to predict mercury speciation in combustion flue gases[J]. Journal of Hazardous Materials, 2014, 264C(2): 380-385.

[19] 吴成军, 段钰锋. 燃煤烟气中汞形态分布的神经网络预测研究[J]. 电站系统工程, 2007, 23(6): 15-18.

WU Chengjun, DUAN Yufeng. Forecasting the distribution of mercury speciation in coal-fired flue gas based on neural networks[J]. Power System Engineering, 2007, 23(6): 15-18.

Prediction of Mercury Emission from Coal-fired Flue Gas Based on Gaussian Process Regression

ZHONG Mei, ZHAO Bingtao, HUANG Shuo

(School of Energy and Power Engineering, University of Shanghai for Science and Technology,Shanghai200093,China)

By selecting the parameters which significantly influence the mercury emission from coal-fired flue gas, the concentration of elemental, oxidized and particulate mercury in flue gas was predicted using Gaussian process regression, a new random process method, while the effects of covariance function and train-test sample ratio on the simulation accuracy were respectively studied. Results show that the squared exponential covariance function is better than rational quadratic and Matern covariance function; the predicted accuracy increases with the rise of train-test sample ratio; Gaussian process regression is superior to traditional modeling methods of nonlinear regression, and displays good generalization ability, which therefore has strong applicability in prediction of mercury speciation in coal-fired flue gas.

coal-fired flue gas; mercury speciation; Gaussian process regression; modeling; prediction

2016-01-12

2016-03-08

国家自然科学基金资助项目(50806049，51278095)；上海市自然科学基金资助项目(08ZR1415100)；沪江基地建设资助项目(D14001)

钟 美(1990-)，女，江西赣州人，硕士研究生，研究方向为燃烧污染物排放控制. 赵兵涛(通信作者)，男，副教授，电话(Tel.)：021-55271751；E-mail: zhaobingtao@usst.edu.cn.

1674-7607(2016)12-0987-06

TK16

A 学科分类号：470.30