应用于高动态接收机的分数阶傅里叶变换实现

董俊翔，赵健康，朱程广，夏 轩

（上海交通大学 仪器仪表工程，上海200240）

应用于高动态接收机的分数阶傅里叶变换实现

董俊翔，赵健康，朱程广，夏 轩

（上海交通大学 仪器仪表工程，上海200240）

针对传统的FFT在高动态环境下难以长时间对高动态信号进行相干累积的难题，以及为了达到对高动态信号进行更有效跟踪的目的，利用FrFT运算瞬时频率随时间呈线性变化的性质，将其应用到高动态接收机中去，对多普勒频率和多普勒频率变化率同时进行补偿。运用基于Closed-form算法实现FrFT运算，并设计高动态接收机信号跟踪环模块，通过基于matlab的一、二维搜索仿真，根据测量得到的结果计算多普勒频率和多普勒频率变化率，将测量值与真实值相比较。仿真证明该跟踪环提高了高动态接收机的跟踪性能和抗干扰能力。

分数阶傅里叶变换；接收机；高动态；Closed-form算法

高动态GNSS系统已经越来越广泛地应用于军事领域之中，尤其是制导武器方面，弹载高动态卫星接收机的难点主要在于导弹的飞行时间短，在飞行过程中导弹弹体的速度、加速度和加加速度的变化非常剧烈，这导致接收机的接收信号它的载波多普勒变化剧烈，从而使接收机信号跟踪难度增大[1]。此时多普勒频移往往会超出一般锁相环的捕获带宽，如果载波多普勒频偏过大，将导致接收机信号跟踪失锁[2]的情况发生。

若在短时间内将加速度视为恒定，则GNSS载波信号等效于一个线性调频信号（Chirp信号）。Chirp信号最主要的性质是瞬时频率随时间呈线性变化。FrFt作为一个有效的Chirp信号检测工具，可以应用到高动态接收机中去，增加其抗噪声干扰，抗多径干扰等能力，并能够更有效地跟踪到高动态信号。使用FrFT可以同时对多普勒频率和多普勒频率变化率分量进行有效补偿，解决了传统的FFT在高动态环境下难以对高动态信号进行长时间相干累积的难题[3-4]。

文中为了实现对高动态信号的分析检测和参数估计，分析了整个接收机系统以及分数阶傅里叶变换在高动态卫星信号跟踪的应用并经由结合Closed-form算法，设计了基于分数阶傅里叶变换的高动态接收机跟踪环模块，通过二维搜索对测试信号进行检测及估值，以达到对其精确跟踪的目的。以此来证明该模块具有能实现跟踪高动态信号的能力。

1 接收机跟踪环设计及分数阶傅里叶变换

文中所设计的接收机整体主要由以下几个部分组成：相关积分模块，信号参数估计模块和相位估计器；相关积分模块负责对伪码对齐后的中频载波信号进行分段相关积分；信号参数估计模块负责计算信号的FrFT，并对载波频率和频率变化率进行估计；相位估计器负责精确计算载波相位，最终对载波NCO进行精确调整，对信号进行跟踪。

初始中频信号经过载波NCO1的初始解调后进入相关积分器，经由FrFT模块处理并计算得到多普勒频率和多普勒频率变化率后进入相位估计器，经过载波NCO2的再解调后留下电文。

FrFT（Fractional Fourier Transform，分数阶傅里叶变换），是广义的传统傅里叶变换[5]，它含有变量p，被称为p阶傅里叶变换。函数x（t）的分数阶傅里叶变换的表达式如下[6]：

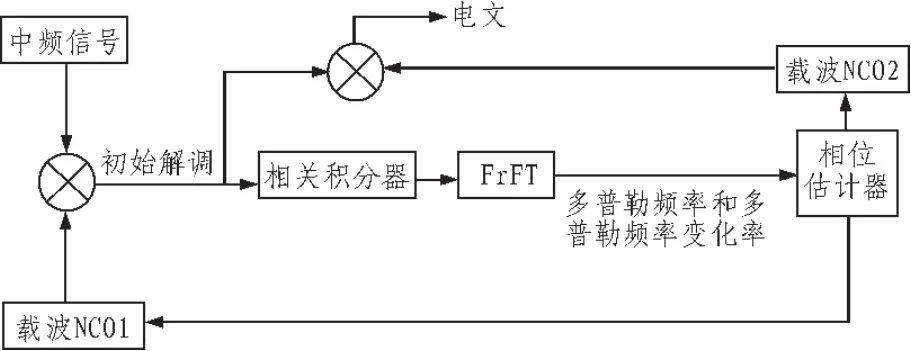
图1 高动态接收机跟踪环设计

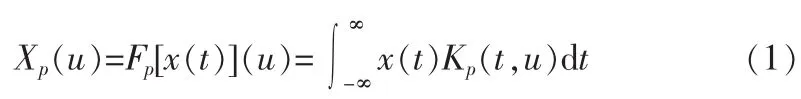
Fp[x（t）]（u）为连续分数阶傅里叶变换的运算符。

变换核

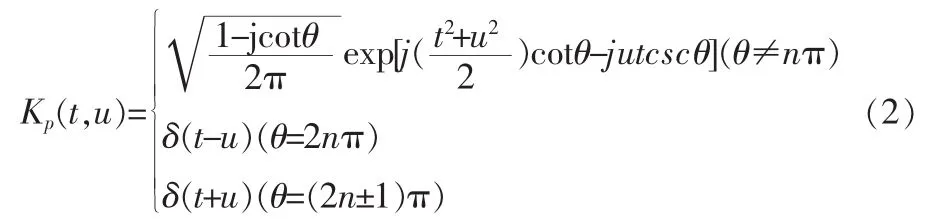
其中0＜|p|＜2，变换角度θ=pπ/2。

变换角度为θ=pπ/2的p阶傅里叶变换的时频图如图1所示。若我们将Fourier变换看作为一种线性算子，在时频平面中当时θ=2nπ+π/2，时域转为频域。那么FrFT算子就是一个可旋转任意角度θ的算子，所以我们可以认为FrFT是广义的傅里叶变换[7]。

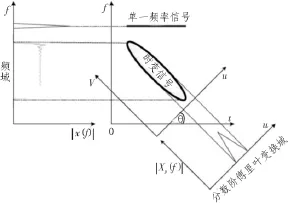
图2 分数阶傅里叶变换时频图

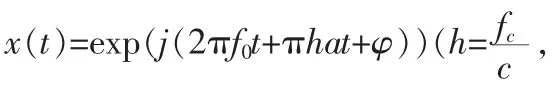
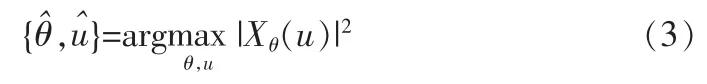
我们使用FrFT，通过上述计算得到了高动态环境下的多普勒频率和多普勒频率变化率，并运用之后的跟踪模块来跟踪高动态信号。

2 算法分析

离散FrFT常用的方法有两种，一种是由Ozaktas提出的分解型算法，将FRFT的定义式积分变换分解为几步简单的计算步骤，然后经过离散化处理得到离散卷积表达式，这样可以利用FFT来计算FrFT；另一种是Pei、Ding等人研究出的一种闭合的DFrFT算法，从连续Fourier变换的特征函数是Hermite函数出发，对特征函数Hermite函数经过离散正交处理，得到DFT矩阵的正交向量，而此正交向量也同样是Hermite特征向量。因此可以构造离散分数阶Fourier变换核矩阵。最后通过对信号的时域和分数阶Fourier域选择合适的采样间隔，得到离散分数阶Fourier变换。

2.1 Ozaktas算法

Ozaktas的分解型算法[10-12]将FRFT定义式的计算过程分为了3个步骤：

可以看出该算法运用了3步FFT的运算来得到分数阶傅里叶变换结果。

2.2 Closed-form算法

我们将采样函数x（t）和输出函数Fp[x（t）]（u）分别按Δt，Δu的间隔进行采样，y（n）=x（n*Δt）；Yα（m）=X（m*Δu），其中n=-N，-N+1，…，N；m=-M，-M+1，…，M；这里值得注意的是我们采样的起始点并不在t=0以及uθ=0处。我们将DC成分置于中心位置[13-14]。于是我们将上式转化为：

这样Yα（m）可逆；当M≥N时将Yα（m）的反变换表示为Fα（m，n）的赫米特转置形式，可以得到[15]：

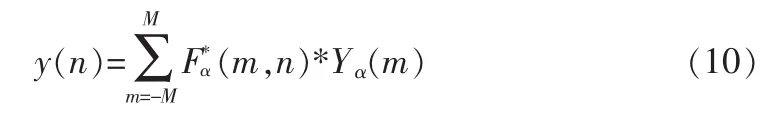
根据式（8）和（9），

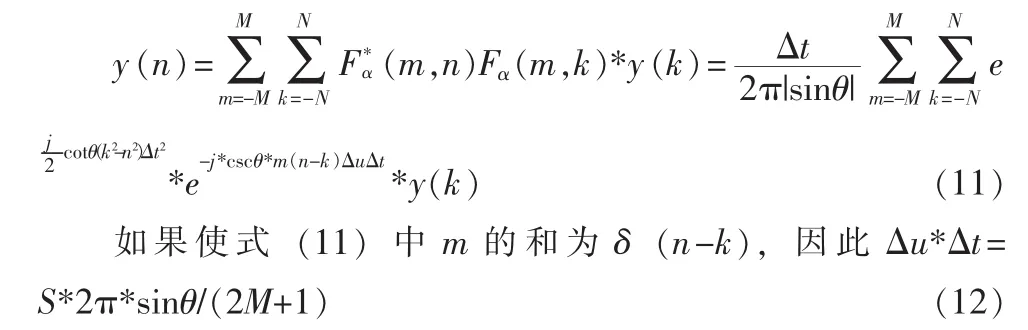
其中|S|是2M+1的一个整数质数，这样的话式（9）可以变成

由式（16）我们可以看出Closed-form算法[13-14]相对于Ozaktas算法更简便，它避免了Ozaktas算法中繁琐的卷积计算，从计算量出发来考虑的话，Closed-form算法的1次FFT运算所需的计算量要远远小于Ozaktas算法卷积运算中用到的3次FFT运算。所以总体来说Closed-form算法计算复杂度相较Ozaktas法要小。

3 算法实现与模块仿真

经过对两种算法的比较，Closed-form算法的结构相对更简单，复杂度更小，故选择该法作为FrFT模块[16]的算法。

具体模块实现步骤如下：

1）原信号与某一线性调频函数相乘；

2）对1）的结果进行Fourier变换（其变元乘以尺度系数）；

3）将2）的结果再与（1）中的线性调频函数相乘；

在仿真测试信号选方面，选择载波信号参数如下：加速度a=200 g，g=10 m/s2，加加速度为0，初始相位为φ≠0，采样频率为fs=10 MHz，中频频率为2.046 MHz，初始多普勒频率为fd0=50 Hz，滤波器点数为512点，信号观测时间为；将载波信号x（t）=exp（j（2πf0t+πhat+φ））作为输入信号，在分数阶傅里叶变换阶次p分别为p=1，p=1.136时，仿真结果分别如图3所示。

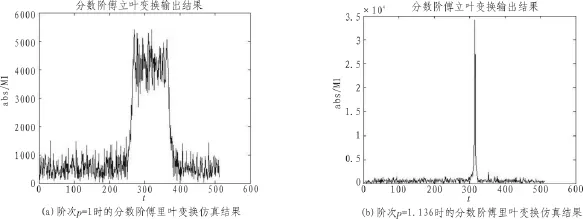
图3 阶次p=1、p=1.136的分数阶傅里叶变换仿真结果

从仿真图中图3可以看出，仿真信号聚集成为一个冲激函数，证明了当且仅当分数阶傅里叶变换阶次p为最佳阶次时，Chirp信号能量聚集为一个冲激函数的结论，即对我们的仿真信号在阶次p=1.136时达到最佳阶次，其信号积聚性最好，从而验证了该模块应用的正确性。

之后我们在一维算法实现的基础上，通过改变分数阶傅里叶变换阶次，对chirp信号分数阶傅里叶变换结果作出二维分布，并对其峰值进行搜索，得到图4所示。

将搜索范围定在p∈[1，1.2]，搜索步长Δp=0.001，时间步长为Δu=0.2 ms，得到峰值坐标为（1.136，315，3.412*104）。由上得出在p=1.136，即旋转角度θ=0.568π=102.24°时可搜索到仿真信号峰值。此时我们将得到的计算结果代入式（4），得到多普勒频率变化率为，多普勒频率为：

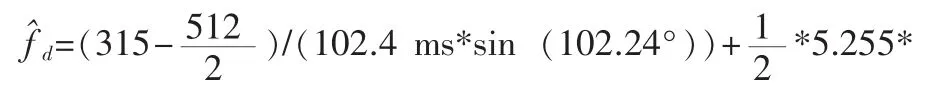
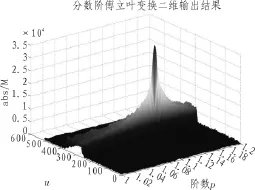
图4 仿真信号分数阶傅里叶变换二维分布图

而当加速度a=100g时（其余参数不变），得到二维分布结果图如图5所示。

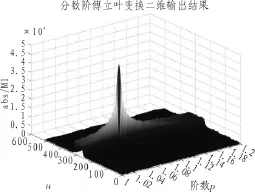
图5 a=100g时，仿真信号分数阶傅里叶变换二维分布图

峰值坐标为（1.068，289，4.514*104），即在p=1.068，旋转角度θ=0.534π=96.12°时可搜索到仿真信号峰值。此时的多普勒频率变化率为，多普勒频率为：

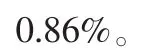
加速度a=50g时，得到二维分布结果图6如下。

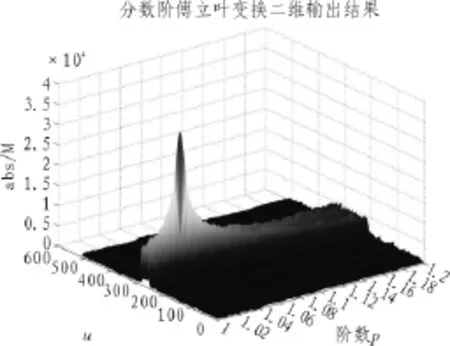
图6 a=50g时，仿真信号分数阶傅里叶变换二维分布图

峰值坐标为（1.034，275，3.611*104），即在p=1.068，旋转角度θ=0.517π=93.06°时可搜索到仿真信号峰值。此时的多普勒频率变化率为，多普勒频率为

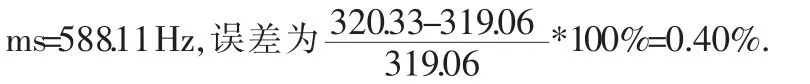
表1 不同加速度下仿真信号多普勒频率的测量值和计算值及其误差

整理以上计算结果，得到下表：

经过对在不同加速度的高动态信号下的多普勒频率估计值与计算真实值的比较，误差都在1%以内，可见该模块可以实现对高动态信号的跟踪，且精度较高。

4 结束语

文中针对接收机的高动态环境下多普勒频移大，跟踪信号相对困难的特点，研究了分数阶傅里叶变换针对跟踪高动态信号的应用，利用Closed-form算法和FrFT运算设计了高动态接收机信号跟踪环模块，并计算得出高动态信号的多普勒频率和多普勒频率变化率，以达到跟踪到高动态信号的目的；该方法在保证精度的同时，尽量减小了运算量，最后给出对仿真测试信号的一维仿真以及二维搜索仿真结果，对该算法应用进行了验证，证实了该算法的可行性和正确性。可以在之后将此模块运用于实际工程项目中去，以体现其满足高动态信号跟踪的精确性和实时性。

[1]潘曦，聂玉平.精确打击武器中高动态跟踪算法及改进研究[J].兵工学报，2011，32（12）：70-74.

[2]曾广裕，申强.弹载高动态卫星接收机环路设计及参数优选[J].北京理工大学学报，2014，34（12）：1299-1304.

[3]王璇，郇浩，赵玉梅，等.高动态GPS接收机捕获技术研究[J].导航天地，2014（2）:14-21.

[4]Simirankit Singh，Rajesh Khanna，Manjeet Singh Patterh. Analysis of FRFT based MMSE Receiver for MIMO Systems [J].Wireless Pers Commun，2013，73:555-562.

[5]陶然，邓兵，王越，等.分数阶傅里叶变换及其应用[M].北京：清华大学出版社，2009.

[6]郭斌，分数阶Fourier变换的基本原理与应用[D].成都：电子科技大学，2006.

[7]金翔，分数阶Fourier变换的高动态信号参数估计[D].重庆：重庆邮电大学，2011.

[8]葛雄强，弹载GPS接收机设计及相关算法研究[D].南京：南京理工大学，2012.

[9]Ashutosh Kumar Singh，Rajiv Saxena.Doppler Estimation from Echo Signal Using FRFT[J].Wireless Oers Commun，2013，72:405-413.

[10]Bargmann V.On a hilbert space of analytic functions and an associated integral transform[J].PartI.Comm.Pure.Appl.Math，1961:187-214.

[11]宋威.基于FRFT水声通信算法的FPGA实现[D].哈尔滨：哈尔滨工程大学，2012.

[12]RAN Tao，LIANG Guang-ping，ZHAO Xing-Hao.An efficient FPGA-based implementation of fractionalfourier transform algorithm[J].J Sign Process Syst，2010，60:47-58.

[13]PEI Soo-Chang，DING Jian-Jiun.closed form discrete fractional and affine fourier transform[J].IEEE Trans Signal Processing，2000，48，（5）:1338-1353.

[14]Sanjay Kumar，Kulbir Singh，Rajiv Saxena.Closed-form analytical expression of fractional order differentiation in fractional fourier transform domain [J].IEEE Circuits Syst Signal Process（2013）32:1875-1889.

[15]刘洋，刘争红，林基明.分数阶傅里叶变换在Chirp调制信号中的应用[J].信阳师范学院 学报：自然科学版，2012，25（2）：178-181.

The application and realization of Fractional Fourier Transformation to high-dynamic GNSS receiver

DONG Jun-xiang，ZHAO Jian-kang，ZHU Cheng-guang，XIA Xuan
（Instrument Engineering，Shanghai Jiaotong University，Shanghai 200240，China）

For the problem that traditional FFT can't accumulate coherently under high-dynamic environment during a longtime period，and in order to track high-dynamic signal more efficiently，we use the feature of FrFT that its instantaneous frequency varies with time，to compensate Doppler frequency and Doppler frequency rate in the high-dynamic receiver. Closed-form algorithm is used to realize FrFT and design the tracking loop of high-dynamic receiver.Through one-dimension and two-dimension simulation based on Matlab，calculating Doppler frequency and Doppler frequency rate，and compare measurement value with the real value.The simulation proves that this tracking loop improve the tracking performance and the ability of anti-interference of the high-dynamic receiver.

fractional Fourier transformation；GNSS receiver；High-dynamic；closed-from algorithm

TN911

A

1674－6236（2016）24-0070-04

2015-12-09 稿件编号：201512113

董俊翔（1991—），男，上海人，硕士研究生。研究方向：高动态接收机。