大型薄壁件的多点支承/定位方法研究
王少锋,洪军,王建国,李宝童,杨朝晖
(1.内蒙古科技大学机械工程学院,014010,内蒙古包头;2.西安交通大学机械制造系统工程国家重点实验室,710049,西安;3.西北工业大学航空学院,710072,西安)
大型薄壁件的多点支承/定位方法研究
王少锋1,2,洪军2,王建国1,李宝童2,杨朝晖3
(1.内蒙古科技大学机械工程学院,014010,内蒙古包头;2.西安交通大学机械制造系统工程国家重点实验室,710049,西安;3.西北工业大学航空学院,710072,西安)
为了解析工件的加工变形与其多支承/定位点布局之间的内在关联,提出了一种新颖的多点支承/定位布局优化方法。利用有限差分方法表征加工变形敏感度的思路,建立了工件加工变形对于支承/定位点布局的解析敏感度表达式,沿减小加工变形最敏感的方向调整支承/定位点分布,可以有效抑制工件加工变形、改善工艺系统刚度。以常见的大型薄壁件的多点支承/定位为研究案例,使用提出的方法对其多支承/定位点初始布局进行了搜索,以此作为全局优化初值,并对优化后的工件加工轨迹变形计算结果进行了比对,结果表明,工件最大加工变形被控制在0.669 4 mm内,相对优化前的1.022 mm减小了34.5%,由此验证了该优化方法的正确性与合理性,并且为多支承/定位点布局优化的创新思维模式提供了理论指导。
薄壁件;多点定位;布局优化
大尺度合金或复合材料薄壁件常用作现代大型飞行器的外蒙皮,其制造过程一般采用先加工后成型工艺,但成型工序所引起的外轮廓大变形极易影响飞行器的气动和隐身性能。
为克服上述问题,逐渐形成了先成型后加工的工艺,但成型后的半成品属于弱刚度薄壳类零件,定位与支承难度增大,且面向刚性体的3-2-1的6点定位原理已不再适用。鉴于此,文献[1]提出了N-2-1定位原理,削弱了薄壁工件在测量和化铣刻线等工艺过程中的变形;文献[2-3]对上述研究进行了拓展,提出了X-2-1动态定位原理,旨在抑制切边等工艺过程中部分定位点逐渐失效所导致的相应加工区域刚度减弱的状况。从目前已查阅文献的内容看,该理论对于如何寻找最优X的研究积累还不够充分。
传统的装夹方案确定依赖于直观判断和经验积累,或者有针对性地对工件弱刚度部位进行加固。其缺陷主要在于:弱刚度部位的针对性加固需长时间地尝试和调整。为此,大量研究围绕着工件装夹定位布局的优化展开。文献[4]以最小化加工位置处的结点变形总和为优化目标,实现了对工件静态支承/定位点布局的优化。文献[5]延伸了文献[4]的研究,将优化目标修正为最小化工件法向变形的平方和。此外,文献[6-7]提出了一种结合有限元计算迭代优化求解的遗传算法,旨在解决工件多支承/定位点的布局优化及定位误差与加工轨迹变形的最小化问题。类似地,文献[8-9]通过遗传算法实现了对工件已知支承/定位点布局的优化。由此可看出,上述研究不约而同地选定定位误差与加工轨迹变形为工件支承/定位点布局优化的目标,但整个优化过程均在工件初始支承/定位点布局已知的条件下进行。然而,恰恰是获取工件支承/定位点布局最优方案对其初始布局,即优化过程的初值异常敏感,因此上述方法往往只是一种改进,而不是全局最优方案。
本文依据课题组前期针对大型薄壁件多支承/定位点初始布局搜索算法的研究成果[10],确定薄壁工件支承/定位点的初始布局,将工件支承/定位点布局优化过程表达为旨在减小加工变形下的多支承/定位点调整问题。同时,设计了优化策略的数学表达,并研究分析了目标最优值与约束边界之间的内在联系,提出了工件多点支承/定位布局优化方法与流程,为装配件的多点支承/定位布局优化提供了新的理论支持与依据。
1 多支承/定位点的初始布局方案
文献[10]以满足工件夹紧力和外形精度为目标,提出了跟随加工区域布置支承/定位点策略,由此为大型薄壁件多支承/定位点布局的全局优化提供了一种可靠的支承/定位点初始布局方案。方案不仅实现了对工件不同加工区域定位误差的针对性的重点防控,而且为进一步优化支承/定位点布局,以此控制工件加工变形、提高工艺系统刚度,为改善加工质量奠定了基础。
本文4.1.1节给出了课题组前期研究案例中针对大型薄壁件定位的多支承/定位点初始布局方案搜索结果。
2 多支承/定位点布局优化策略设计
自然界植物的生长过程特性,如向重性、向水性和向氧性等,可被看作是一个具有功能目标自适应性的最优化过程。受此启发,将大型薄壁件多支承/定位点布局的优化转化为如何沿减小加工变形的最敏感方向调整支承/定位点分布的问题,由此实现工件加工路径处的加工变形逐渐趋于最小。显然,搜索减小加工变形的最敏感方向是该优化研究的关键。
2.1 优化策略设计
借鉴优化设计中的灵敏度概念,通过计算比较工件加工变形相对各支承/定位点单位量移动下的变化率,移动方向选为对应工装各支承/定位柱的驱动方向,由此确定减小加工变形的最敏感支承/定位点及其移动方向,并以此作为装配件多点支承/定位布局优化过程中应遵循的优化策略,即调整相应支承/定位点沿减小工件加工变形的最敏感方向移动。
为便于计算,使用中心差分对上述优化策略进行计算,以支承/定位点沿x轴移动的灵敏度为例
(1)
式中
Pi、Δpx分别表示第i号支承/定位点空间坐标与其沿x轴的单位移动增量。
支承/定位点沿y轴移动的灵敏度计算类似。
2.2 优化策略决策实例
基于式(1)所示工件多支承/定位点布局优化策略的数学内涵,构造如图1所示的4支承/定位点的工件加工变形敏感度计算模型,以此分析相应支承/定位点沿x、y轴的移动对载荷受力处工件变形的影响,并实现对应灵敏度的计算。以#4支承/定位点的分析为例,分别将各支承/定位点沿x、y轴分别正、负偏置Δpx、Δpy时,分析对工件表面法向载荷受力处变形的影响,可得对应敏感度的计算结果,如表1所示。其他支承/定位点的计算类似。
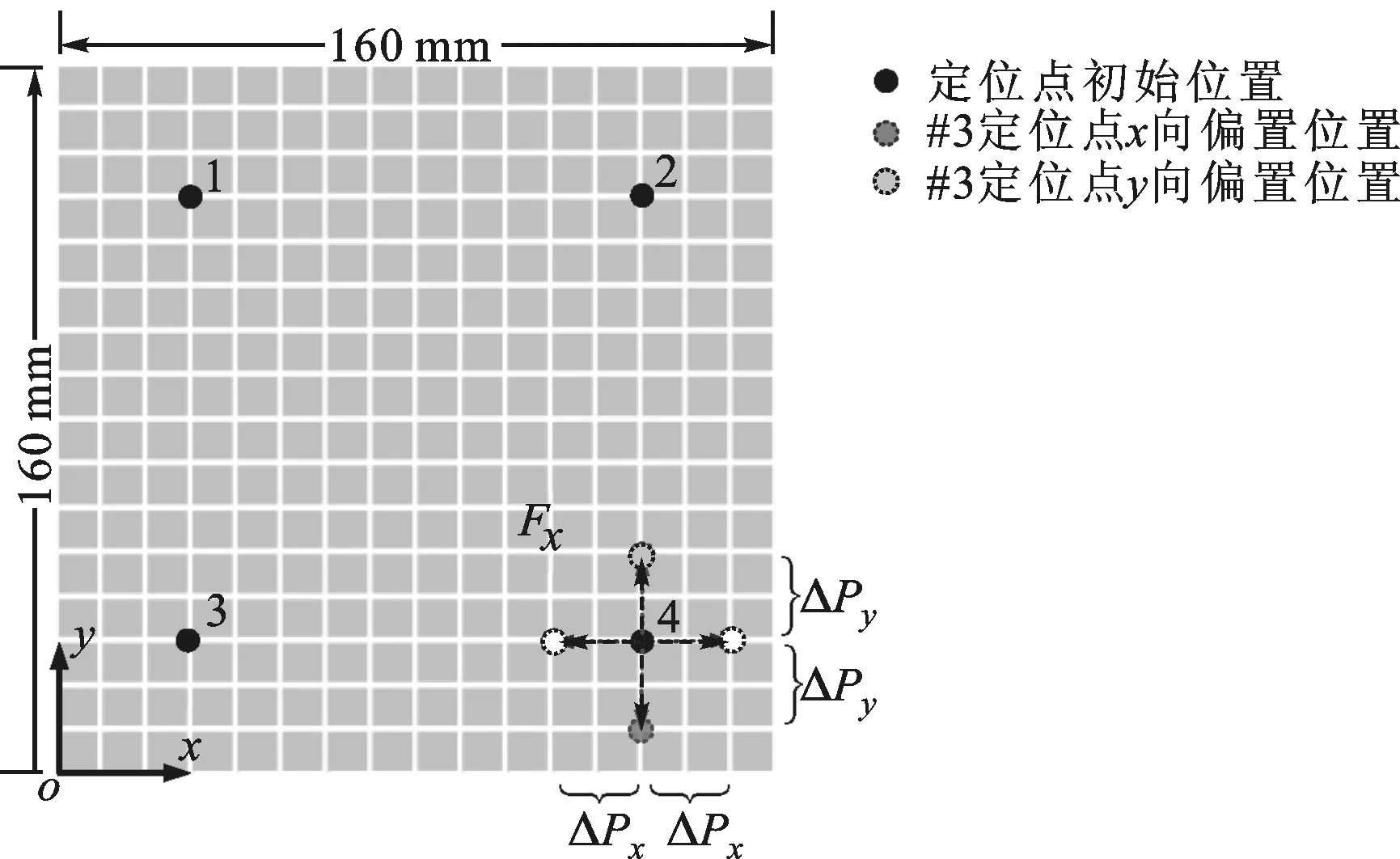
材料:Al Alloy;弹性模量:70 GP;泊松比:0.3;单元:Shell[8]; 厚度:3 mm; ΔPx:20 mm; ΔPy:20 mm图1 #4支承/定位点工件加工变形敏感度计算模型

定位/支承点SxSy1900×10-5900×10-52240×10-4535×10-43535×10-4240×10-44438×10-3438×10-3
由此可以看出,工件表面法向载荷受力处变形的波动相对#4支承/定位点沿y轴的单位增量移动最为敏感(Sy=4.38×10-3),而#1支承/定位点沿x、y轴的单位增量移动对于削弱载荷受力处变形几乎无影响(Sx=Sy=0.9×10-5)。显然,调整支承/定位点布局的决策为沿y轴正向移动#4支承/定位点。
3 多支承/定位点布局优化方法
多支承/定位点布局优化方法的研究关键在于:找出一个合适的多点支承/定位布局P,在满足所有约束时,使工件加工载荷下的工件加工变形最小。显然,数学简化多点支承/定位工装原型、构建优化模型(包括优化目标和约束条件)与优化算法是该研究的重点。
3.1 多点支承/定位阵列工装的数学简化
为了便于对文献[10]所提出的多点柔性支承/定位阵列工装原型进行数学描述,将其简化为图2所示的通用模型。
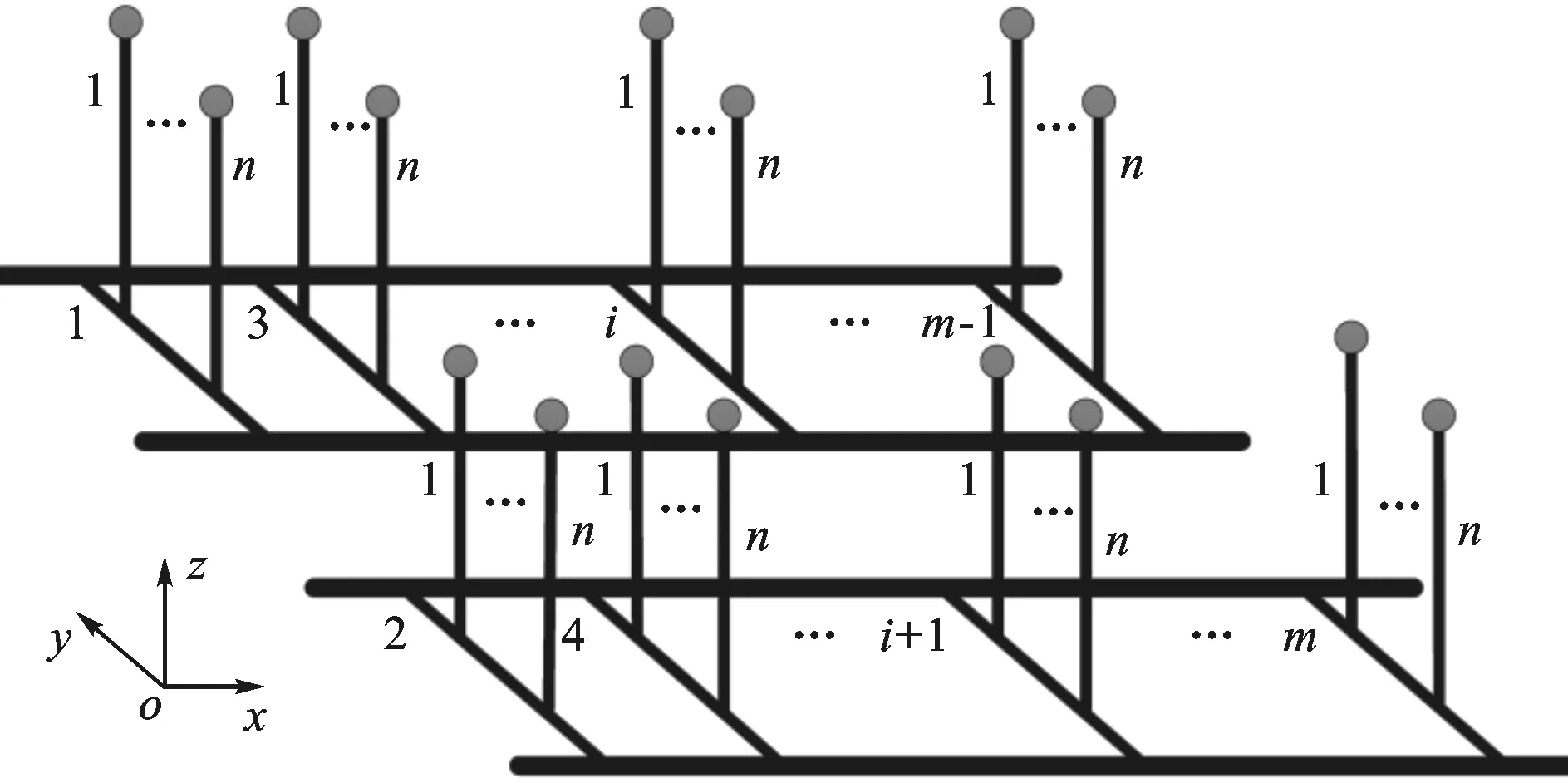
图2 多点柔性支承/定位阵列工装简化模型
如图2所示,假设该系统具有滑枕的总数为m,每个滑枕具有n个支承/定位单元,则工件的任意支承/定位点布局形式可表示为
P=(P1,P2,…,Pm)
(2)
式中:Pi=(pi,1,pi,2,…,pi,n)T(i=1,2,…,m)表示第i号滑枕上n个支承/定位单元末端定位点坐标;pi,j=(pi,j_x,pi,j_y,pi,j_z)T(j=1,2,…,n)为相应支承/定位单元末端定位点的空间坐标。显然,同一滑枕上各支承/定位点具有相同的x轴坐标。为此,以pi_x表示对应同一滑枕上的支承/定位点x坐标,那么第i号滑枕上第j号滑座上定位/支承单元末端定位点的空间坐标可表示为
pi,j=(pi_x,pi,j_y,pi,j_z)T
(3)
3.2 构建优化模型
3.2.1 构建目标函数 为描述大型薄壁件装夹定位后抗拒加工变形的能力,构建优化目标如下
(4)
式中:kD为加工路径各离散点处的系统工艺刚度;δm为工件加工路径上不同位置的加工变形;Fp为加工载荷;n为加工路径上各受力点处的法向量。
由式(4)可以判断支承/定位点布局的优劣:若对应加工位置周围存在足够合理的支承/定位点布局,则该处刚度趋于无穷大,说明该加工位置已被充分支承与定位,加工变形近似为0;若该刚度很小,表明对应加工位置处变形较大,加工质量扰动大,应调整支承/定位点布局。因此,该指标反映了工件在相应加工位置处对支承/定位点布局优化的需求程度。
基于文献[10]得到的支承/定位单元初始布局P,在保证加工区域支撑刚度和装夹精度的前提下,调整支承/定位点分布以减少实际加工变形,进而使式(4)所给优化目标取得极大值的优化过程可表述为如下优化目标函数
max(kD)=f(P1,P2,…,Pm)
(5)
3.2.2 构建约束条件 为了避免不当支承/定位点布局所引起的支承/定位夹持机构间的几何运动干涉,对图2所示支承/定位夹持机构各驱动组件的运动极限进行约束如下。
(1)滑枕移动约束。第i号滑枕沿x轴的移动范围受第i-1、i+1号滑枕所在位置限制,即
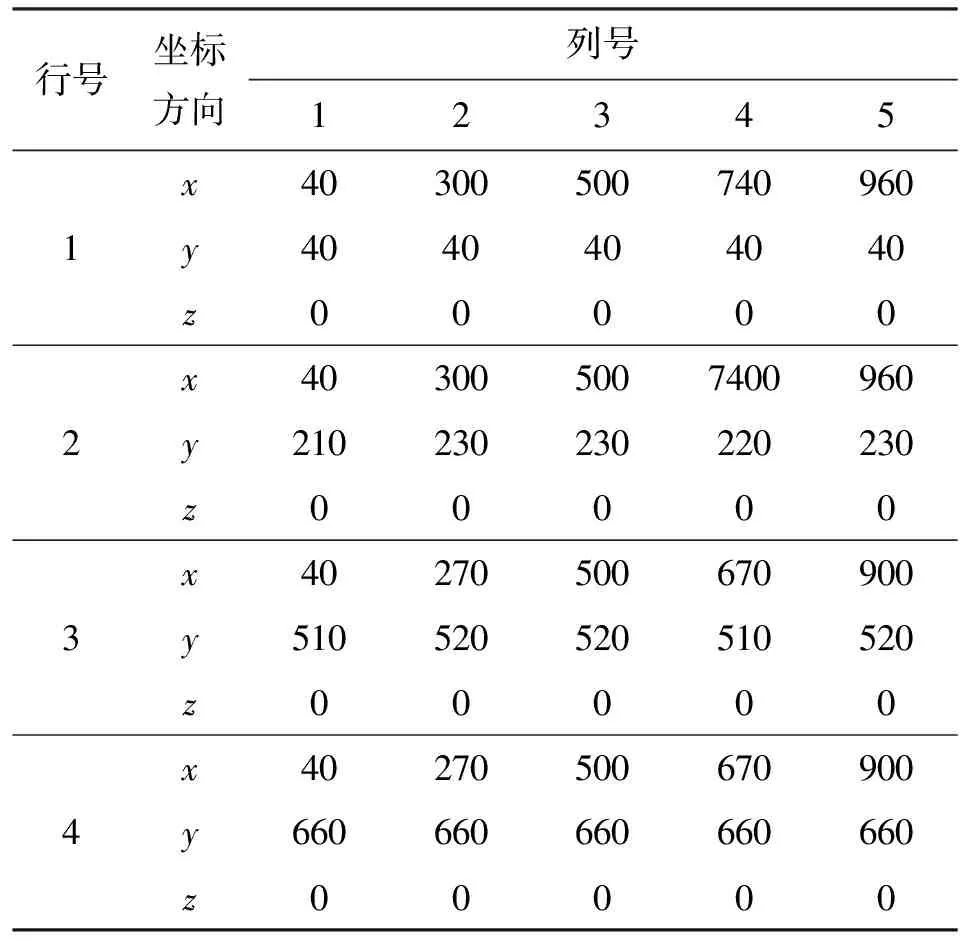
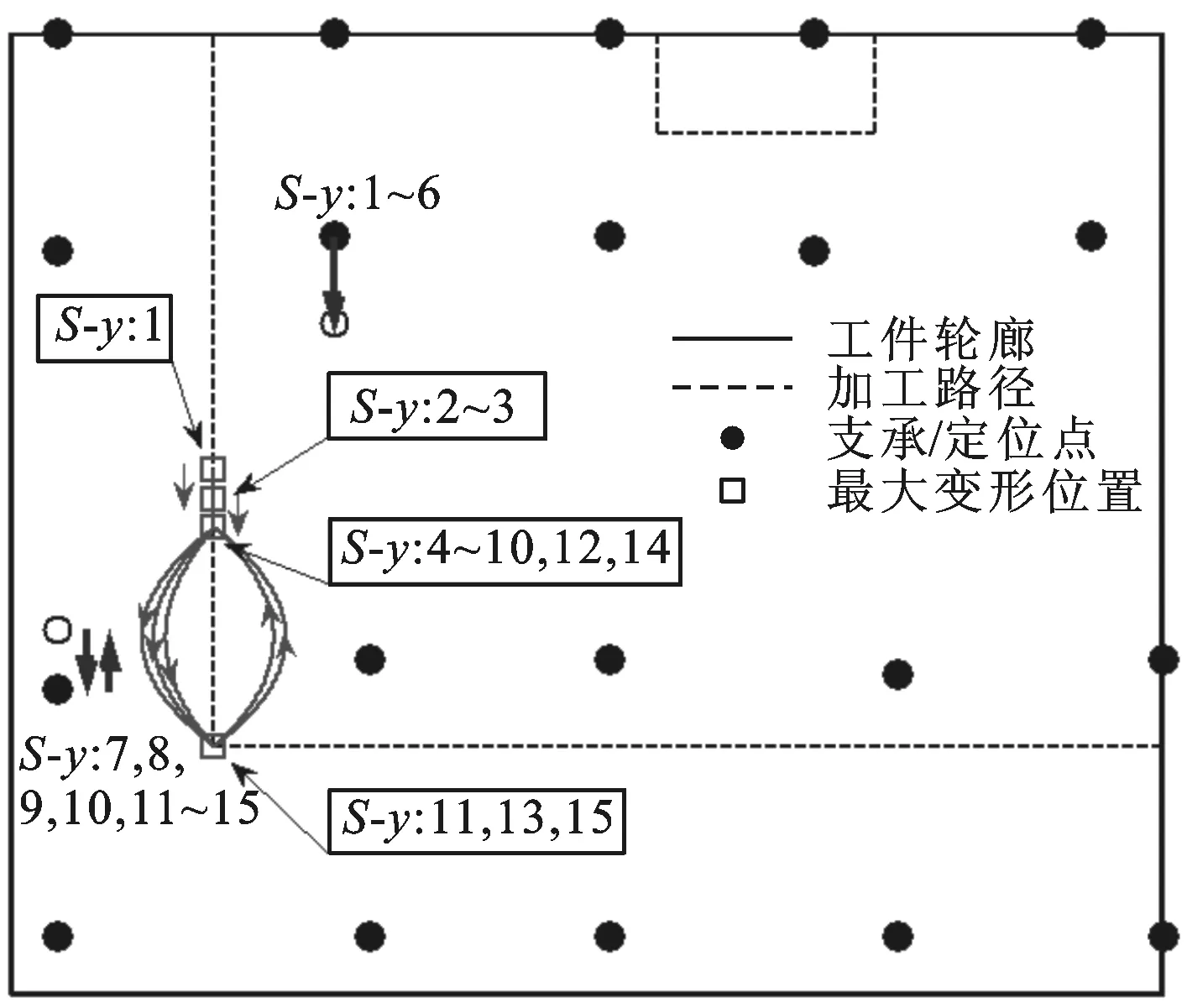
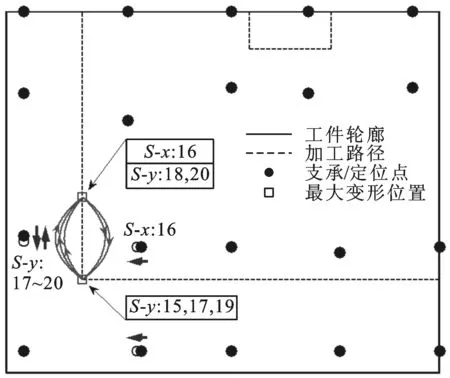
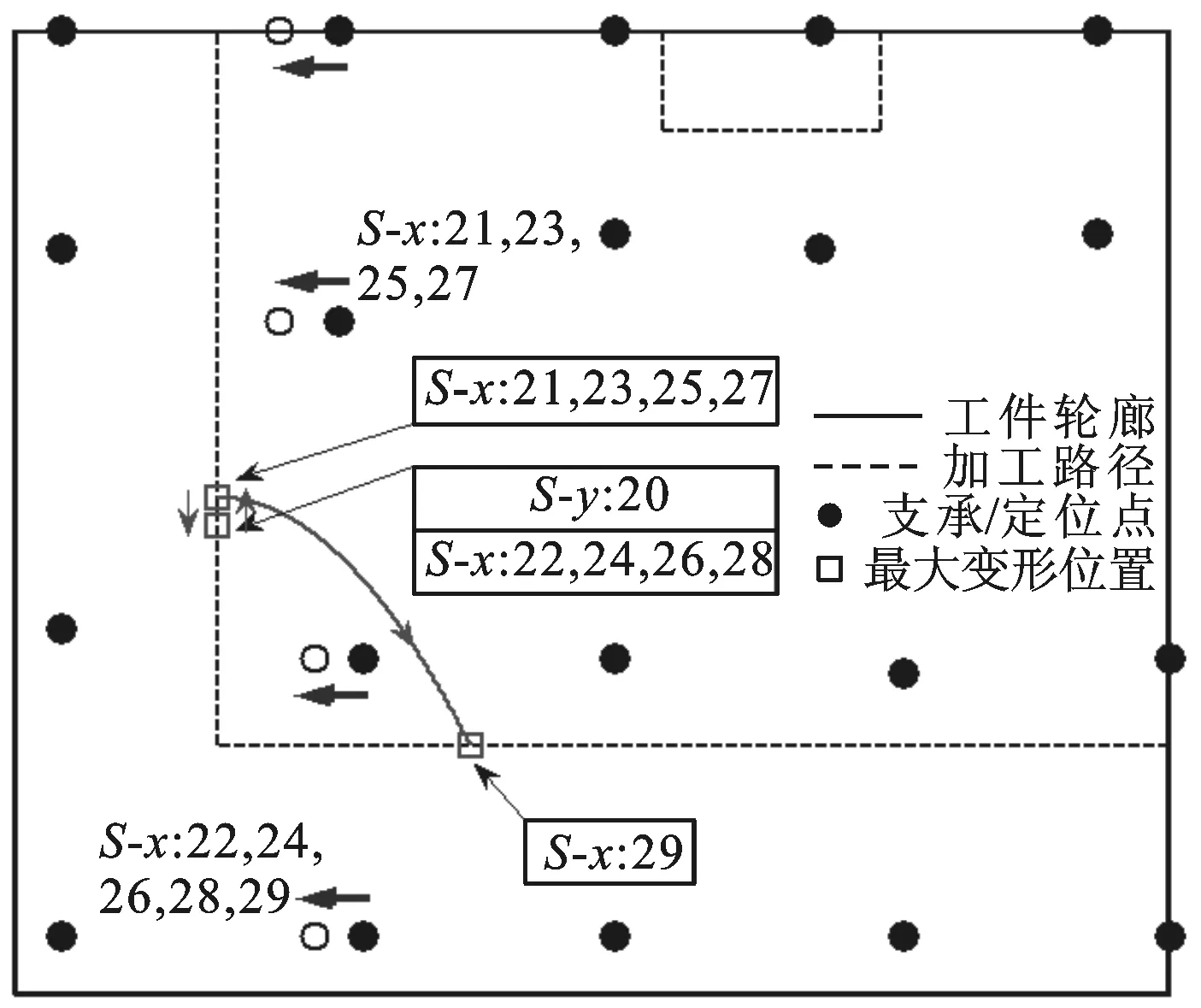
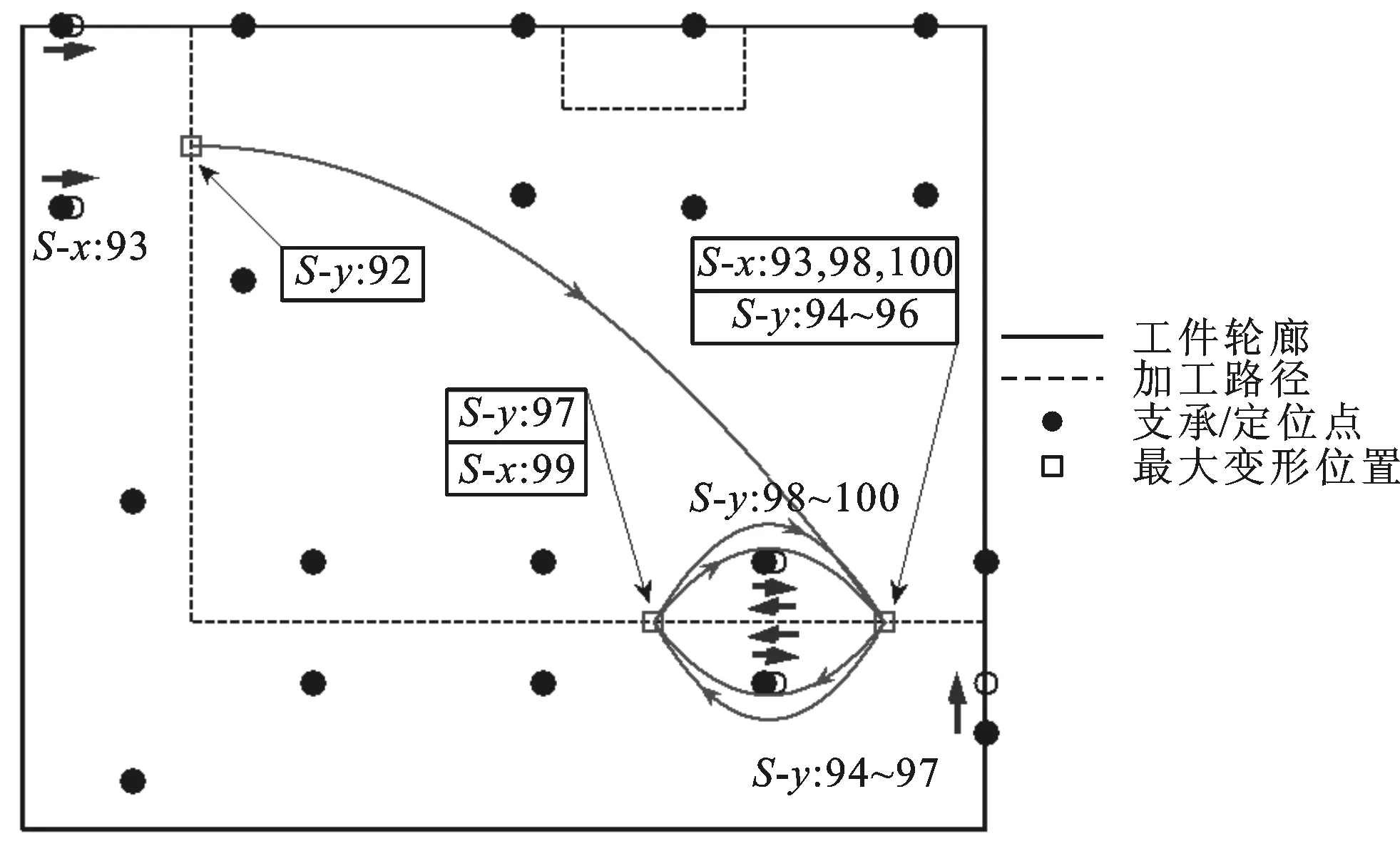
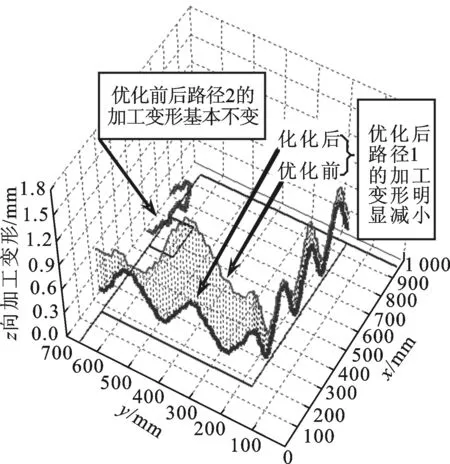
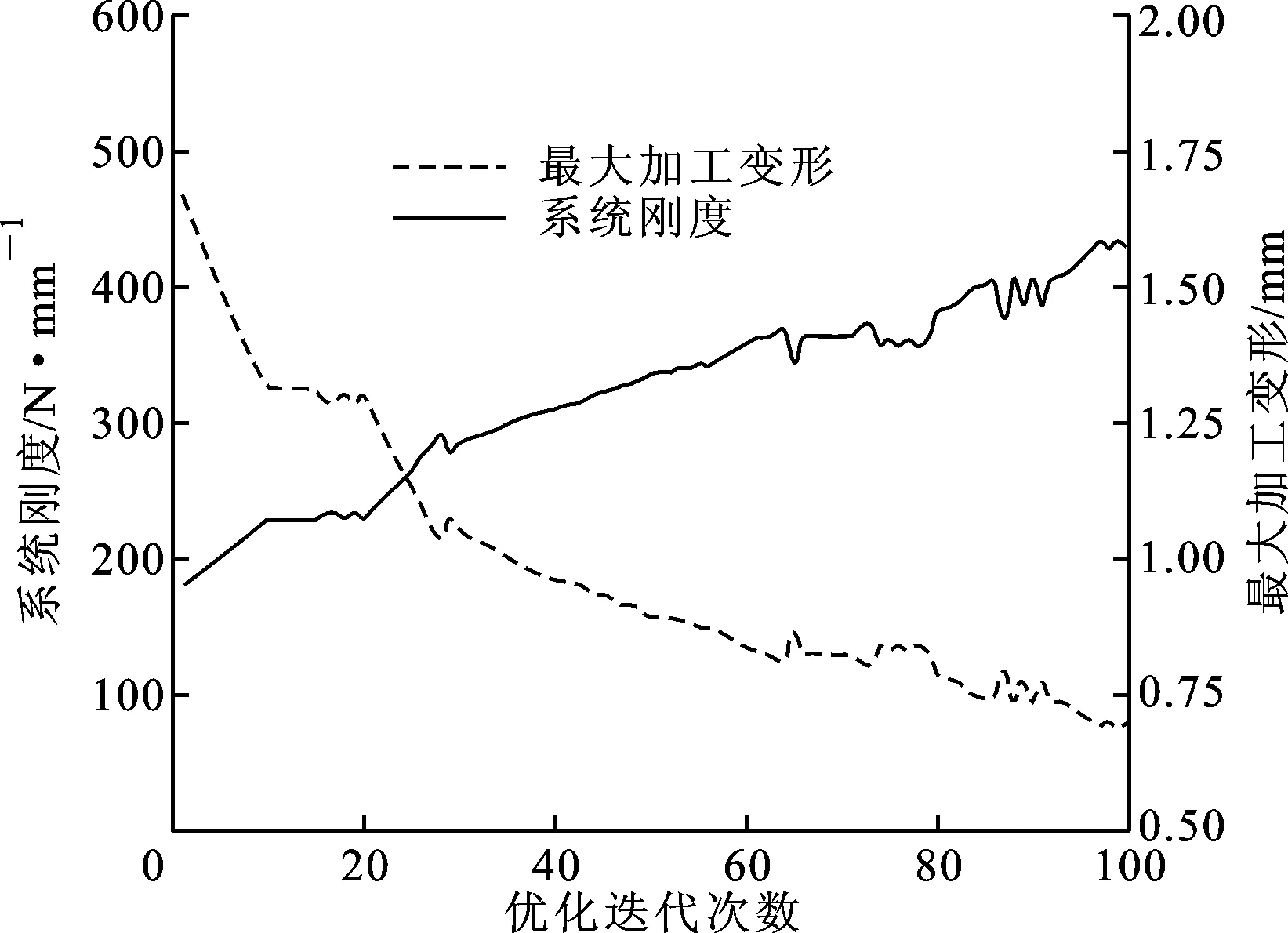
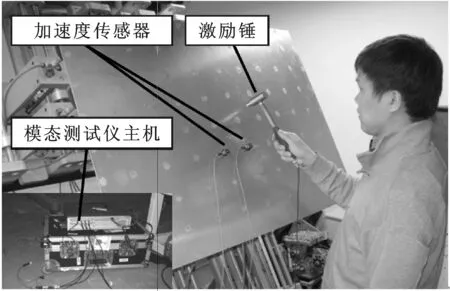
pi-1_x+umin i=2,3,…,m-1 (6) 式中:umin为相邻滑枕接触时相应支承/定位单元末端定位点间的最小x向间距。 最外侧两滑枕(i=1,m)的移动范围受工装系统基座外缘x向尺寸的限制,即 xmin (7) pm-1_x-umin (8) 式中:xmin、xmax分别为第1、第m号滑枕沿x轴正负向所能移动到的最远处。 (2)滑座移动约束。第i号滑枕上的第j号滑座沿y轴的移动范围受第j-1、第j+1号滑座上支承/定位单元所处位置的限制,即 pi,j-1_y+vmin i=1,2,…,m;j=2,3,…,n-1 (9) 式中:vmin为相邻滑座接触时相应支承/定位单元末端定位点间的最小y向间距。 最外侧两滑座(j=1,n)的移动范围受工装基座外缘y向尺寸的限制,即 ymin (10) pi,n-1_y-vmin (11) 式中:ymin、ymax分别为第i(i=1,2,…,m)号滑枕上第1、第n号滑座沿y轴正、负向所能移动到的最远处。 3.3 构建优化算法 通过求解优化变量P1,P2,…,Pm,可确定支承/定位点分布,从而实现对工件加工变形及其动刚度的控制。需特别注意的是:支承/定位点的灵敏度计算通常只需考虑加工载荷附近区域,因距离较远的支承/定位点对加工变形几乎无任何影响,这样可大大节省计算资源,提高优化效率。由此,该优化过程实现的具体步骤如下。 步骤1 初始化设置。设置支承/定位点初始布局P=(P1,P2,…,Pm),具体过程见文献[10]。 步骤2 于支承/定位点布局P的工件有限元数值分析建模,求解工件的加工变形。 步骤3 求解工件加工路径各离散加工位置处的系统工艺刚度。提取加工路径各离散加工位置处最大变形,求解对应各离散加工位置处刚度kD,若kD>kD_max,表明该支承/定位单元分布P满足工件加工质量需求,优化计算结束;否则,需对支承/定位点布局进行调整。 步骤5 沿x轴方向调整加工路径上最大加工变形处周围支承/定位点位置。利用式(1)计算各支承/定位点沿x方向移动的灵敏度Sy[f(P)],沿影响加工变形最敏感方向移动相应支承/定位点。若移动后支承/定位点满足约束条件式(6)~式(8),则支承/定位点未触界,重构支承/定位点布局P=(P″1,P″2,…,P″m),返回步骤2;否则,支承/定位点触界,优化过程结束,布局P为最终优化结果。 上述多点支承/定位布局优化流程如图3所示。 图3 多点支承/定位布局优化流程 本节沿用文献[10]所构建的有限元数值计算模型,并基于文献[10]所得到的大型薄壁件多支承/定位初始布局方案,修正模型中支承/定位点的初始位置。沿工件加工路径依次施加300 N法向加工载荷分量,利用2.1节所设计的优化策略,通过3.3节所构建的优化算法对相应支承/定位点进行调整,以此展示其逼近最大加工变形位置的整个过程。最终获取对应加工位置的最优刚度,以此削弱加工变形,进一步验证本文所提优化算法的正确性和合理性。 4.1 理论计算分析 4.1.1 多支承/定位点初始布局搜索 算例依据本课题组前期针对大型薄壁件多支承/定位点初始布局搜索算法的研究[10],在保证工件可靠夹持及对工件不同加工区域定位误差有针对性重点防控的前提下,确定了工件支承/定位点的初始布局,其空间坐标如表2所示。 表2 支承/定位点空间坐标 mm 图4 调整阶段I 图5 调整阶段II 图6 调整阶段III 图7 调整阶段XII 图8 优化前后加工路径的加工变形对比 图9 加工变形与工艺系统刚度变化历程 4.1.3 工件加工路径变形分析 工件加工路径上各离散加工位置处的加工变形在优化前后的对比如图8所示。由此可看出:加工路径1的加工变形在优化后大大减小,而路径2的加工变形基本不变。原因在于:相对加工路径1,加工路径2周围的支承/定位点密度更大,最大加工变形未出现在路径2上,优化过程未改变加工路径2周围的支承/定位点分布。同时,最大加工变形与工艺系统刚度的变化趋势如图9所示,可以发现,最大变形比优化前减小了34.5%,且大大提高了工件加工过程的刚度,保障了工件的加工质量。 4.2 模态实验测试分析 4.2.1 模态实验系统组成 如图10所示,构建了模态测试系统,主要由薄壁件、多点柔性支承/定位阵列工装、086D50型PCB力锤(208C03型力传感器)、压电式ICP三向加速度传感器、LMS SCADAS III多通道数采、Test.Lab模态分析软件和计算机组成。该测试系统主要用于获取外界激振下薄壁件与多点柔性工装系统在对应支承/定位点布局下的响应信号,以及完成信号的滤波、放大等功能。 图10 模态测试系统示意框图 4.2.2 模态实验方法设计 采用单点激励、多点拾取的方法对工件模型进行动态特性测试。选择薄壁件上表面的中央位置作为激励点,在工件模型上布置99个测点。在LMS分析软件中,以薄壁件一个角点为原点建立坐标系,输入所有测点的三维坐标,建立模型结构的点框图。图11显示了模态实验测试环境。 图11 模态实验测试环境 在建立测点点框模型之后,完成多通道动态信号采集系统的连接,测试中使用2个三向加速度传感器获取三维振型。对每个测量点进行5次敲击测试,取平均值,确保每次数据采集准确可靠。在完成一组测试之后将传感器移至下一组测量点,最终获得整个模型99个测点的频响函数。将频率带宽设置为0~200 Hz,利用LMS软件中的Time MDOF模块对测试结果进行分析。 4.2.3 模态参数识别、分析与系统修正 如图12所示,提取对应本节所得到的支承/定位点布局下薄壁件的1、2阶模态振型,特别显示1阶模态振型。由此可以看出:工件在宽度方向上的刚度较差,其下侧边缘较长的悬出部分产生了弯曲振动变形;工件的长度方向相对宽度方向刚度较弱,产生了弯曲振动变形,且中间无支撑区域产生了沿垂直方向的弯曲。表3对其前2阶振型的特点进行了描述。 图12 薄壁件1阶模态振型 阶数频率/Hz振型描述特点140516左侧边缘、中间无支撑区域沿垂直方向弯曲垂直方向弯曲265203左下部边缘沿宽度方向扭曲垂直方向微弱扭曲宽度方向扭曲 4.2.4 支承/定位点布局修正 鉴于本实验室多点支承/定位系统工装结构设计的约束,选择整体向左移动最外侧第2号滑枕上的p2,1和p2,2,以此修正支承/定位点布局。实验结果表明,与未调整p2,1和p2,2时薄壁件固有频率相比,其1阶固有频率由未修正时的40.516 Hz提高到修正后的43.782 Hz。图13所示为模态振型实测结果,修正后,其变形演变为左下边角的翘曲,且中间无支承/定位点部位振型明显变小,较好地抑制了振动。 图13 薄壁装配件1阶模态振型(修正后) 本文紧密结合薄壁件多点支承/定位布局优化的数学建模这一基础理论问题,提出了多支承/定位点布局的优化策略——沿减小加工变形最敏感方向调整支承/定位点分布。在此基础上,提出了抑制加工变形的多点定位布局优化方法。以常见的大型薄壁件的多点支承/定位为案例,并以本课题组前期研究中所提出的跟随加工区域布置定位点的方法,对大型薄壁件的多支承/定位点初始布局进行搜索,以此作为优化初值,进而全程展示了多支承/定位点布局的优化流程。对优化后的工件加工轨迹变形计算结果进行了比对,发现最大加工变形被控制在0.669 4 mm内,相对优化前的1.022 mm减小了34.5%,由此验证了该优化方法的正确性与合理性。此外,通过模态实验进一步对相应支承/定位点布局下工件固有频率以及振型等进行了测试,并以此提出了修正支承/定位点布局或添加辅助支承/定位点抑制振动变形的方法。 [1] CAI W, HU S J, YUAN J. Deformable sheet metal fixturing: principles, algorithms, and simulations [J]. J Manuf Sci Eng, 1996, 118: 318-324. [2] 胡福文, 李东升, 李小强, 等. 面向飞机蒙皮柔性夹持数控切边的定位仿真系统及应用 [J]. 计算机集成制造系统, 2012(5): 993-998. HU Fuwen, LI Dongsheng, LI Xiaoqiang, et al. Locating simulation for aircraft skins NC trimming based on flexible holding fixture [J]. Computer Integrated Manufacturing Systems, 2012(5): 993-998. [3] 胡福文, 李东升, 李小强, 等. 蒙皮柔性夹持数控切边的工艺设计方法 [J]. 北京航空航天大学学报, 2012, 38(5): 675-680. HU Fuwen, LI Dongsheng, LI Xiaoqiang, et al. Process planning of aircraft skins NC trimming based on reconfigurable fixture [J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(5): 675-680. [4] MENASSA R J, DEVRIES W R. Optimization methods applied to selecting support positions in fixture design [J]. Trans ASME J Eng for Ind, 1991, 113: 412-418. [5] CAI W, HU S J, YUAN J X. Deformable sheet metal fixturing: principles, algorithms and simulations [J]. Trans ASME J Manufact Science and Engng, 1996, 118: 318-324. [6] WU N H, CHAN K C. A genetic algorithm based approach to optimal fixture configuration [J]. Comput Ind Engng, 1996, 31(3/4): 919-924. [7] KULANKARA K, SATYANRAYANA S, MELKOTE S N. Iterative fixture layout and clamping force optimization using the genetic algorithm [J]. Transactions of the ASME Journal of Manufacturing Science and Engineering, 2002, 124: 119-125. [8] 秦国华, 张卫华, 周孝伦. 夹紧方案的数学建模及夹紧力的优化设计 [J]. 机械科学与技术, 2008, 24(4): 438-446. QIN Guohua, ZHANG Weihua, ZHOU Xiaolun. Modeling and optimal design of fixture clamping scheme [J]. Mechanical Science and Technology, 2008, 24(4): 438-446. [9] 陆俊百. 飞行器大型薄壁件柔性工艺装备系统研究 [D]. 北京: 清华大学, 2010. [10]王少锋, 洪军, 王建国, 等. 大型薄壁件多点定位的初始布局优化算法研究 [J]. 西安交通大学学报, 2016, 50(5): 38-44. WANG Shaofeng, HONG Jun, WANG Jianguo, et al. Initial distribution optimization for multi-point location of large-scale thin-wall component [J]. Journal of Xi’an Jiaotong University, 2016, 50(5): 38-44. [本刊相关文献链接] 王少锋,洪军,王建国,等.大型薄壁件多点定位的初始布局优化算法研究[J].2016,50(5):38-44.[doi:10.7652/xjtuxb 201605006] 吴继琸,朱刚贤,陆斌,等.自愈合效应对光内送粉激光变斑熔覆成形薄壁件的影响[J].2016,50(1):145-150.[doi:10.7652/xjtuxb201601022] 周强,刘志刚,洪军,等.卡尔曼滤波在精密机床装配过程误差状态估计中的应用[J].2015,49(12):97-103.[doi:10.7652/xjtuxb201512016] 王少锋,张进华,刘志刚,等.大型飞机机身壁板装配位姿调整系统的运动规划[J].2011,45(3):102-106.[doi:10.7652/xjtuxb201103019] 丁建军,蒋庄德,李兵,等.线结构光扫描测头误差分析与补偿方法[J].2008,42(3):286-290.[doi:10.7652/xjtuxb2008 03007] (编辑 杜秀杰) Multi-Point Location Method of Large-Scale Thin-Wall Component WANG Shaofeng1,2,HONG Jun2,WANG Jianguo1,LI Baotong2,YANG Zhaohui3 (1. School of Mechanical Engineering, Inner Mongolia University of Science and Technology, Baotou, Inner Mongolia 014010,China; 2. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China;3. School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China) To analyze the relationship between workpiece machining deformation and multi-point location/support distribution, a new optimization method is proposed to amend multi-point location/support distribution. Depending on the idea of representing the sensitivities of machining deformation with finite difference method, the analytic expressions for sensitivities of machining deformation with respect to location/support distribution are established. The location/support distribution is adjusted along the most sensitive direction to restrain machining deformation and improve process system stiffness. A multi-point location of large-scale thin-wall component is taken as an example, and the searched initial distribution of location/support point is regarded as the initial value for the global optimization of multi-point location/support distribution. A comparison with non-optimized workpiece machining path deformation shows the maximum machining deformation is reduced by 34.5%, which is limited below 0.669 4 mm far less than the non-optimized value of 1.022 mm. thin-wall component; multi-point location; distribution optimization 2015-12-16。 作者简介:王少锋(1980—),男,讲师;洪军(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金青年基金资助项目(51405377)。 时间:2016-03-11 10.7652/xjtuxb201606019 TH161 A 0253-987X(2016)06-0122-08 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160311.1711.002.html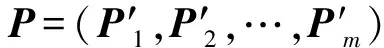

4 算例研究


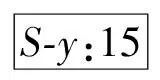
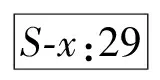
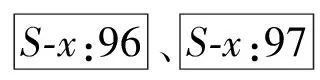




5 结 论

