用于孤立数字语音识别的一种组合降维方法
宋青松,田正鑫,孙文磊,吴小杰,安毅生
(长安大学信息工程学院,710064,西安)
用于孤立数字语音识别的一种组合降维方法
宋青松,田正鑫,孙文磊,吴小杰,安毅生
(长安大学信息工程学院,710064,西安)
针对孤立数字语音识别的噪声鲁棒性问题,提出了一个组合降维方法。该方法由梅尔频率倒谱系数(MFCC)特征提取、线性降维、受限玻尔兹曼机(RBM)、Softmax分类器4个功能模块依次组成;基于主成分分析(PCA)基本原理对MFCC特征向量实现了降维并且统一维度的目的;通过RBM对降维后的特征向量进行学习,改善了后端Softmax分类器的分类性能,RBM的预训练由对比散度算法完成,微调过程使用共轭梯度算法。采用TI-46孤立数字语音库和NOISEX-92典型噪声数据库对方法进行了测试,实验结果表明,该方法可以获得96.09%的正确识别率,相对于常规神经网络识别方法,噪声鲁棒性得到了提高。
语音识别;主成分分析;受限玻尔兹曼机
孤立数字语音识别有着广阔的研究和应用价值,诸如动态时间规整(dynamic time warping,DTW)、隐马尔科夫(hidden markov model,HMM)、矢量量化(vector quantization,VQ)、主成分分析(principal component analysis,PCA)、人工神经网络(artificial neural network,ANN)等方法用于求解孤立数字语音识别问题[1-3]。DTW算法基于动态规划的思想解决发音长短不一的模板匹配问题,但是存在运算量大、识别性能依赖端点检测精度等不足。VQ算法基于聚类识别,运算量小但是最优码书较难得到。PCA算法可以实现数据降维,并且能够统一数据维数,但本质上是一种基于最优正交变换的线性降维方法,对于非线性问题难以得到满意的结果。ANN算法特别是Hinton等提出的受限波尔兹曼机(restricted Boltzmann machine,RBM)及其快速学习算法,在模式识别与分类问题中表现出良好的非线性降维与特征表征能力,但是通常需要适当的特征参数提取等预处理手段配合使用[4]。常用的数字语音信号特征通常是高维的,分类前需要对数据进行降维处理。因此,为改善数字语音识别效果,本文基于PCA线性降维和RBM特征学习基本原理,提出了一种用于孤立数字语音识别的组合降维方法,待分类的数字语音信号依次经过线性降维和RBM非线性特征表征处理,最终识别性能得到改善。
首先阐述组合降维识别方法涉及的线性降维、RBM、Softmax分类器等功能模块,然后给出用于RBM预训练和微调的学习算法,最后在TI-46数据库和NOISEX-92噪声数据集上验证了所提算法的先进性。
1 组合降维识别方法
1.1 功能模块组成
组合降维识别方法由梅尔频率倒谱系数(Mel-frequency cepstral coefficients,MFCC)特征提取、线性降维、RBM、Softmax分类器4个功能模块组成,如图1所示。首先提取MFCC及其一阶差分作为原始语音信号的特征参数,然后对MFCC进行线性降维,再将降维后的特征参数输入RBM进行特征学习,学习的结果作为后端Softmax分类器模块的输入,Softmax输出分类结果。

图1 组合降维语音信号识别方法的功能模块
1.1.1 MFCC特征提取 MFCC[5]是将人耳的听觉特性与语音产生机制相结合的一种特征参数,在语音识别领域具有广泛应用。标准MFCC参数只反映语音参数的静态特性,MFCC差分则反映语音参数的动态特性,在语音特征中加入表征语音动态特性的MFCC差分,通常能提高系统的识别性能。因此,本文提取标准MFCC及其一阶差分共同作为待识别语音信号的特征参数。MFCC特征提取的结果是得到一个F行24列大小的特征向量矩阵T,F为当前语音信号的帧数。
1.1.2 线性降维 MFCC特征提取结果存在两个问题:一是每个语音信号由不同数量的帧组成,导致矩阵T大小不同;二是F取值大导致矩阵T过大,存在降维计算需要。因此,基于PCA基本原理对特征矩阵T作进一步变换,实现其降维并且大小一致的目的。使用的方法是将T转置,再与原矩阵T相乘,得到24×24的方阵S;求S的特征值并从大到小排序,取前两个特征值对应的特征向量并串接,得到一个48维的特征向量,作为线性降维后当前语音信号的特征向量。
1.1.3 受限波尔兹曼机 降维后的特征向量输入RBM模块进行特征学习,学习结果输出到后端Softmax分类器中。
RBM本质上是通过无监督学习最大可能地对输入数据进行特征表征。RBM由可见层和隐含层构成,如图2所示。可见层由一组可见单元v构成,用于输入数据;隐含层由另一组隐藏单元h构成,用于输出无监督学习获得的对输入数据的特征表示。RBM的特点是层内无连接,层间全连接。

图2 RBM结构示意图[6]
1.1.4 Softmax分类器 采用Softmax分类器实现RBM输出特征分类。记类标y可以取r个不同的值,对于训练集{(x(1),y(1)),…,(x(m),y(m))},类标签为y(n)∈{1,2,…,r},r为分类数。对于给定的输入x(n),用假设函数hλ(x(n))针对每一个类k估算出概率值p(y(n)=k|x(n)),k=1,…,r。hλ(x(n))输出一个r维的列向量(和为1),每行表示为当前类的概率。
定义假设函数hλ(x(n))[7]为
(1)
式中:λ1,λ2,…,λr是模型参数。将x(n)分为第k类的概率记为
(2)
对于样本x(n),选择概率p(y(n)=k|x(n);λ)值最大的对应的类别k作为当前样本的分类标签,并与样本本身的标签做比对,如果一致则分类正确,否则分类错误。
1.2 学习算法
组合降维识别方法的学习分为RBM预训练和微调两部分。
1.2.1 RBM预训练 预训练的目的是对线性降维后的特征向量作无监督学习,以获取更好的特征表征。鉴于可见层节点语音特征向量服从高斯分布的特点,使用高斯-伯努利RBM,定义能量函数[6]
(3)
式中:θ={ai,bj,wij}是RBM模型参数;ai和bj分别是可见层节点i和隐含层节点j的偏置;wij是可见层节点i和隐含层节点j之间的连接权值。当参数确定时,可以得到联合概率分布
P(v,h;θ)=exp(-E(v,h;θ))/Z
(4)


(5)
RBM的模型参数使用最大似然准则通过无监督训练得到,训练的目标函数为
(6)
对目标函数求偏导,可以得到权值的更新公式
Δwij=Edata(vihj)-Emodel(vihj)
(7)
式中:Edata(vihj)是训练集数据对应的可见层和隐含层状态的期望值;Emodel(vihj)是对所有可能的(v,h)的模型期望值。
Emodel(vihj)直接计算很困难,通常采用对比散度进行近似计算[4]。可见层单元的状态被设置为任取一个训练样本,算法开始,通过一步吉布斯采样获得“重构”的可见单元状态〈vi〉recon,再用〈vi〉recon更新隐含层单元状态,得到〈hj〉recon。学习率ε大使收敛速度快,但过大会引起算法不稳定,ε小可消除不稳定,但会减慢收敛速度,为克服该矛盾,在更新参数时增加动量项c,使得本次参数修改的方向由上一次参数修改方向和本次的梯度方向一起决定,而不是完全由当前样本下的似然函数梯度方向决定。因此,各参数的更新准则为
Δwij=cΔwij+ε(〈vihj〉data-〈vihj〉recon)
(8)
Δbi=cΔbi+ε(〈vi〉data-〈vi〉recon)
(9)
Δaj=cΔaj+ε(〈hj〉data-〈hj〉recon)
(10)
使用重构误差对RBM进行评估。重构误差就是以训练数据作为初始状态,根据RBM的分布进行一次吉布斯采样所获得的重构样本与原始样本的差异。
1.2.2 微调 RBM预训练完成之后,对RBM和Softmax进行微调。为改善学习效率,在微调开始的前5次,只对Softmax分类器的模型参数进行有监督学习,从第6次开始对RBM和Softmax的全部参数进行学习。
代价函数定义为
J(λ)=
(11)
式中:1{·}是一个指示性函数,当{·}中的值为真时,该函数值为1,否则为0。采用PRP共轭梯度算法求解minJ(λ)无约束最优化问题[8]。
微调结束后得到RBM和Softmax最终的模型参数。给定任意的孤立数字语音信号,依次通过图1所示的各个功能模块,可以输出分类结果。
2 实验设计与结果分析
2.1 实验设计
组合降维识别方法的性能测试在TI-46数字语音数据库上进行,语音信号的采样频率为12.5 kHz,16 b量化。选择3 000个样本作为训练集,0~9共10个数字各300个样本,选择另外的1 000个样本作为测试集,每个数字各100个[9]。
MFCC特征提取模块中帧长取256,帧移为80,窗函数使用汉明窗。RBM预训练过程中,可见层输入数据归一化到(0,1)之间,连接权重初始化为正态分布N(0,0.01)随机数,可见层和隐含层的偏置均初始化为0。将数据集分成小批量进行预训练,每个批量为50个。学习率ε为0.001,最大训练次数为50次,动量项c在前5次训练中取0.5,之后取0.9。微调过程PRP共轭梯度算法中线性搜索步长为3,微调次数为200次。
计算机配置为内存4 GB、双核i5、处理器2.67 GHz、GPU为 NVIDIA GT540。
设计一个3层前馈神经网络(feedforward neural network,FNN)取代图1中RBM和Softmax分类器两个功能模块,采用相同的训练集和测试集,相同的MFCC特征提取模块和线性降维模块,训练采用经典的误差反向传播算法作对比实验。通过交叉验证确定隐层神经元数量为78的FNN对应最佳识别性能,即FNN模型结构取为48-78-10。记录FNN识别结果,与本文方法结果作对比。
2.2 结果分析
本文方法与FNN方法各自独立完成10次实验,测试结果见表1。在无噪声情形下,FNN方法正确识别率平均为93.07%,而本文方法为96.09%,优于前者。图3给出了无噪声情形下本文方法和FNN方法针对0~9单个数字语音信号的正确识别率及其标准差,针对数字0、1、3、5、6、7、8、9,本文方法正确识别率均高于FNN方法,而且正确识别率的标准差均小于FNN的,表明无噪声情形下本文方法与FNN方法相比,不仅正确识别率高而且性能更加平稳。

图3 本文方法与FNN方法针对10个孤立数字语音信号的性能测试结果
对测试集以20 dB的信噪比(signal-noise ratio,SNR)分别加入白噪声、汽车噪声、工厂噪声及F16机舱噪声等4类典型噪声用于评价方法的噪声鲁棒性[10],结果见表1,FNN方法4类噪声情形下正确识别率的平均结果由93.07%降低为91.44%,降低了1.63%,而本文方法的正确识别率从96.09%降低为95.08%,降低了1.01%,小于前者,表明有噪声情形下本文方法性能下降慢于FNN,并且降低后本文方法的正确识别率为95.08%,仍然高于FNN的91.44%。

表1 本文方法与FNN方法正确识别率测试结果

(a)白噪声情形

(b)汽车噪声情形
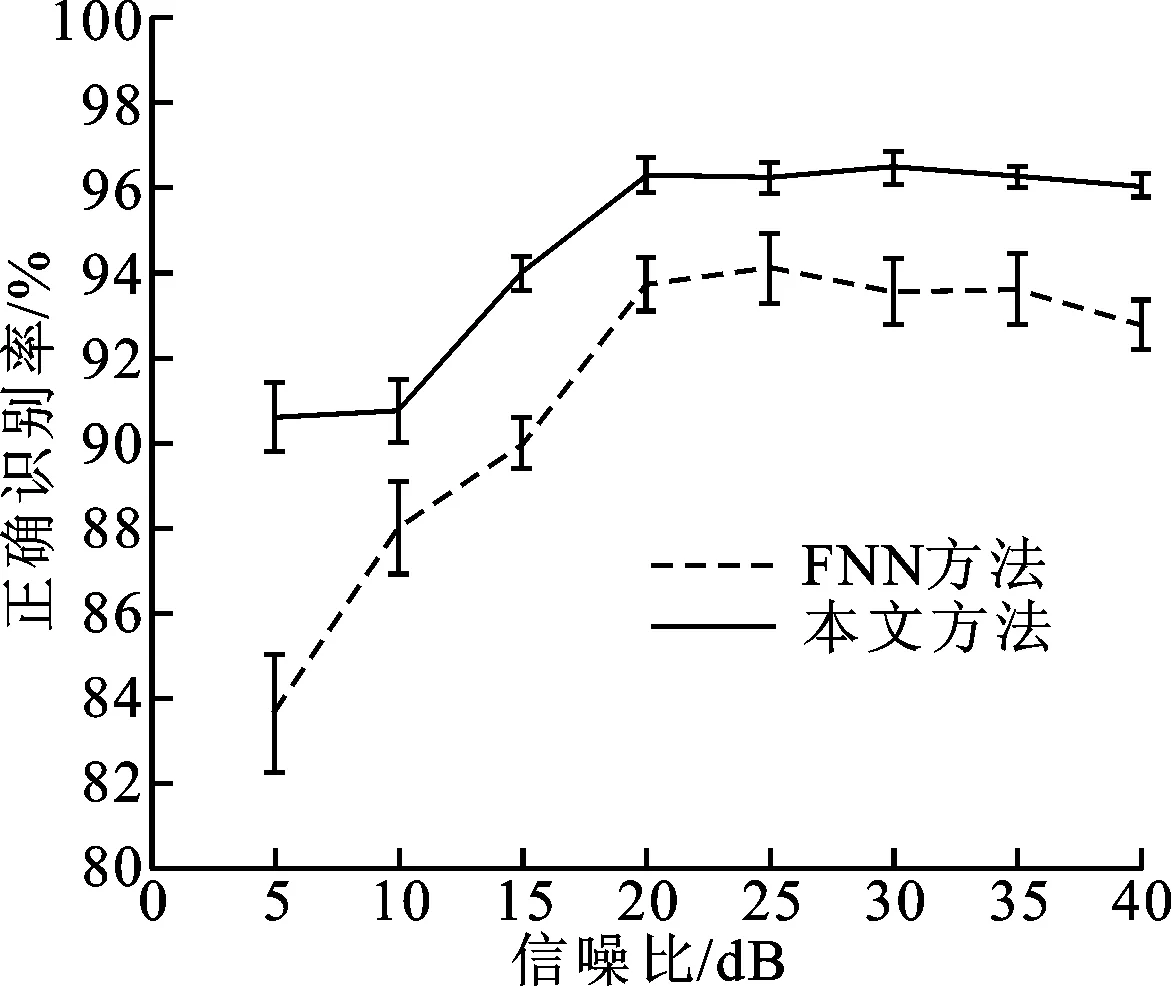
(c)工厂噪声情形
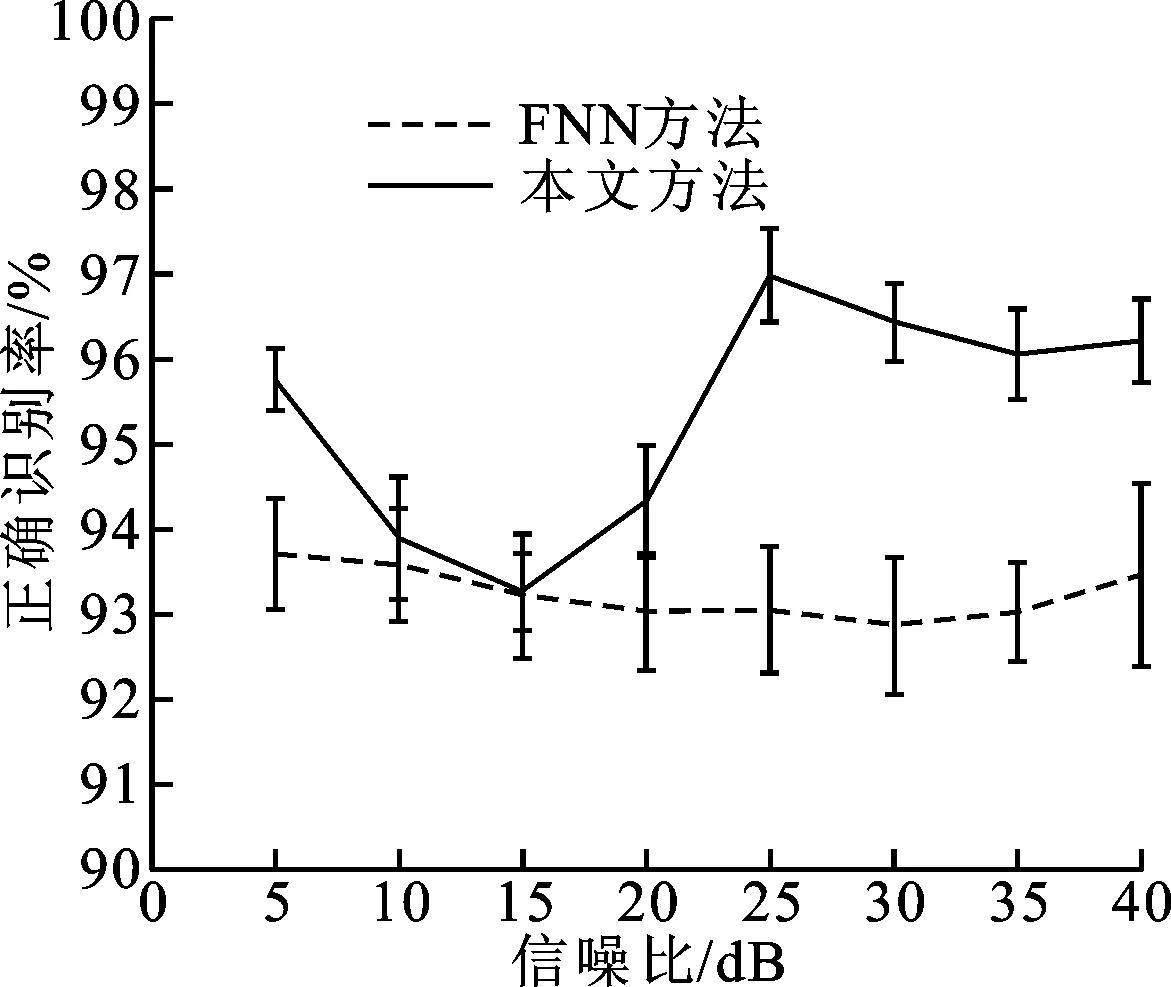
(d)F16机舱噪声情形图4 典型噪声情形下本文方法与FNN方法性能测试结果
图4给出了5~40 dB信噪比范围内本文方法和FNN方法在上述4类典型噪声情形下正确识别率的测试结果。如图4a~图4c所示,白噪声、汽车噪声、工厂噪声3种情形下,本文方法的正确识别率均高于FNN方法,而且前者的正确识别率标准差比后者要小,说明本文方法的性能更加平稳。图4d表明F16机舱噪声情形下两种方法在10~20 dB范围内的正确识别率无明显差别,但是本文方法获取的正确识别率标准差更小,性能更平稳。
上述实验结果表明,针对孤立数字语音识别问题,在有、无噪声两种情形下,本文方法均能够获得优于FNN方法的正确识别率,具有一定的噪声鲁棒性,并且性能平稳。
3 结 论
针对孤立数字语音识别问题,基于PCA线性降维和RBM特征学习基本原理,提出一种组合降维语音识别方法。该方法具有MFCC特征提取、线性降维、RBM特征自动表征等方法的综合优势,特别地,基于PCA基本原理对MFCC特征向量实现了降维并且统一维度的目的,通过RBM非线性特征学习,改善了后端Softmax分类器的分类性能。基于TI-46孤立数字语音库和NOISEX-92典型噪声数据库的测试结果表明,本文方法能够获得优于常规前馈神经网络的正确识别率,并且识别性能更平稳,具有改善的噪声鲁棒性。
[1] SCHAFER P B, JIN D Z. Noise-robust speech recognition through auditory feature detection and spike sequence decoding [J]. Neural Computation, 2014, 26(3): 523-556.
[2] SLOIN A, BURSHTEIN D. Support vector machine training for improved hidden Markov modeling [J]. IEEE Transactions on Signal Processing, 2008, 56(1): 172-188.
[3] TAKIGUCHI T, ARIKI Y. PCA-based speech enhancement for distorted speech recognition [J]. Journal of Multimedia, 2007, 2(5): 13-18.
[4] HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks [J]. Science, 2006, 313(5786): 504-507.
[5] FANG Z, ZHANG G, SONG Z. Comparison of different implementations of MFCC [J]. Journal of Computer Science and Technology, 2001, 16(6): 582-589.
[6] 张春霞, 姬楠楠, 王冠伟. 受限波尔兹曼机 [J]. 工程数学学报, 2015(2): 159-173. ZHANG Chunxia, JI Nannan, WANG Guanwei. Restricted Boltzmann machines [J]. Chinese Journal of Engineering Mathematics, 2015(2): 159-173.
[7] SALAKHUTDINOV R, HINTON G E. Replicated Softmax: an undirected topic model [C]∥Proceedings of the Advances in Neural Information Processing Systems. Cambridge, MA, USA: MIT Press, 2009: 1607-1614.
[8] 黄海, 林穗华. 一个PRP型共轭梯度法的收敛性 [J]. 西南大学学报: 自然科学版, 2012, 34(3): 28-31. HUANG Hai, LIN Suihua. Convergence of a PRP type conjugate gradient method [J]. Journal of Southwest University: Natural Science Edition, 2012, 34(3): 28-31.
[9] DODDINGTON G R, SCHALK T B. Speech recognition: turning theory to practice [J]. IEEE Spectrum, 1981, 18(9): 26-32.
[10]VARGA A, STEENEKEN H J M. Assessment for automatic speech recognition: II. NOISEX-92: a database and an experiment to study the effect of additive noise on speech recognition systems [J]. Speech Communication, 1993, 12(3): 247-251.
(编辑 武红江)
Combined Dimension Reduction Method for Isolated Digital Speech Recognition
SONG Qingsong,TIAN Zhengxin,SUN Wenlei,WU Xiaojie,AN Yisheng
(School of Information Engineering, Chang’an University, Xi’an 710064, China)
A combined dimension reduction method is proposed to improve the noise-robustness in isolated digital speech recognition. The method consists of four functional modules in sequence: a Mel frequency cepstrum coefficient (MFCC) module for feature extraction, a linear dimension reduction module, a restricted Boltzmann machine (RBM) module, and a Softmax classifier module. The dimension of the MFCC feature vector is reduced and its dimensionality is unified based on the basic principle of the principal component analysis (PCA); the obtained reduced features are learned by RBM in order to improve the classification performance of the end Softmax classifier module. The pretraining of the RBM is completed by the contrastive divergence algorithm and the finetuning process is fulfilled by the conjugate gradient algorithm. The proposed method is verified on the TI-46 isolated digital speech corpus and the NOISEX-92 noise datasets. The experimental results and comparisons with the conventional feedforward neural network methods show that the proposed method achieves at a 96.09% recognition accuracy and obtains improved noise robustness.
speech recognition; principal component analysis; restricted Boltzmann machine
2015-11-30。 作者简介:宋青松(1980—),男,副教授。 基金项目:国家自然科学基金资助项目(61201406);中国博士后科学基金资助项目(2013M531998);中央高校基本科研业务费专项资金资助项目(310824162022,310824162021)。
时间:2016-04-15
10.7652/xjtuxb201606007
TP301.6
A
0253-987X(2016)06-0042-05
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160415.1612.008.html

