人体下肢行走关节连续运动表面肌电解码方法
陈江城,张小栋
(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
人体下肢行走关节连续运动表面肌电解码方法
陈江城,张小栋
(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
为实现人体下肢步态动作的连续识别,提出了一种利用表面肌电信号进行下肢关节运动角度连续解码的方法。首先利用光学运动捕捉实现下肢关节运动角度的计算,然后采集下肢运动相关主力肌肉的表面肌电信号并提取其活动强度信息;在此基础上,基于受限玻尔兹曼机构建深度自动编码器(DAE),实现多路表面肌电信号强度时间序列的低维空间编码和最优特征提取;最后,利用BP神经网络建立特征量与关节矢状面运动角度之间的非线性回归模型。实验结果表明:该方法提取的信号特征信息优于传统的主量分析方法,采用提出的模型能够更精确地估计下肢关节连续运动角度,其估计值与真实值的均方误差较传统方法降低25%~35%。研究结果为人机交互接口技术的开发、实现下肢可穿戴智能装备的生物电连续控制、提高人机运动平稳性奠定了基础。
表面肌电信号;连续运动识别;玻尔兹曼机;深度自动编码器;BP神经网络
新一代具有强大交互能力的人机合作智能装备是目前机器人领域研究的热点,如康复训练机器人、助力助行外骨骼机器人及智能假肢等[1-3]。随着生物信息技术的发展,通过脑电、肌电等生物电信号来实现人与协同对象和外界环境的交流,将生物电蕴含的人体运动信息作用于机器人,是人机交互实现的新途径。表面肌电信号(sEMG)是从肌肉表面通过电极记录的生物电信号,蕴含了丰富的肌肉活动与肢体运动信息,具有采集技术成熟、时间分辨率高、记录无创等优点,是现代人机交互接口技术中最常用的生物电信号。
近年来,国内外已有不少关于利用表面肌电信号进行肢体运动信息解码的研究,包括运动状态辨识和运动量连续解码。对于运动状态的辨识,过去研究重点多集中在表面肌电信号的特征提取、表达以及多模式分类算法的改进上[4-7]。由于基于分类模型只能对有限的离散动作进行辨识,识别结果仅作为机器人运动模式切换的控制信号,影响人机运动的平稳性和协调性。相比之下,表面肌电信号的运动量连续解码能够弥补这一不足。
目前,采用生物力学建模[8]、神经网络[9-11]和高阶多项式拟合[12]等方法构建表面肌电信号与运动量之间的函数模型。生物力学建模方法从肌骨系统运动机理出发,建立表面肌电信号与关节运动量之间的关系,过程复杂,实用性降低。因此,通过神经网络回归方法建立表面肌电信号与运动量之间的映射关系就显得简单快捷。然而,在利用神经网络进行模型回归之前,如何从复杂的、多通道的表面肌电信号中提取连续的、鲁棒的和无冗余信息的信号特征是问题关键。对于多路表面肌电信号的处理,现有方法多采用主分量分析(PCA)获得表面肌电信号的最优特征表达[10,12]。由于PCA是一种基于线性子空间映射的降维方法,不能够发掘隐藏在高维空间中的非线性结构,因此对于随机性高且具有强非线性特性的表面肌电信号存在局限。
本文以人体下肢行走关节角度连续识别为目标,在对人体下肢运动捕捉和关节角度计算方法研究的基础上,同步获取关节角度信息和主力肌肉表面肌电信号,并构造深度自动编码网络(DAE)进行多路表面肌电信号的非线性降维和特征提取,最终建立表面肌电信号特征与关节运动角度之间的BP网络回归模型。实验结果验证了本文方法的正确性和可靠性。
1 人体下肢运动捕捉与关节角度计算
人体下肢运动系统具有关节隐蔽、自由度多及不存在固定基座的特点,增加了关节运动信息准确捕捉的难度。目前对于人体运动信息的捕捉和分析,主要有视觉方式和非视觉方式两种[13],相比而言,视觉方式可以采集更准确和丰富的信息。本节给出一种基于光学捕捉的关节运动角度计算方法,基本过程如图1所示。

图1 人体下肢关节运动计算过程
1.1 关节中心的确定与局部坐标系的建立
从机构学角度看,人体下肢系统包括骨盆、大腿、小腿和足4个肢体节段,由髋、膝和踝关节连接,为了准确描述肢体节段的姿态及相对关系,除世界坐标系外,需要建立各自的局部坐标系。利用光学运动捕捉系统记录16个体表关键标记点在世界坐标系下的三维运动轨迹,标记点布置与世界坐标设置如图2所示,其中x轴方向指向人体正前方,z轴竖直向上,两者构成平面为矢状面,而x轴与y轴构成水平面,y轴与z轴构成额状面。
(1)基于标记点的位置坐标确定髋、膝和踝关节中心点的位置坐标(以肢体左侧为例)。对于膝关节和踝关节,以关节内外侧标记点的中点作为关节中心,即
pkjc=(p5+p6)/2
(1)
pajc=(p7+p8)/2
(2)
式中:pkjc为膝关节中心位置矢量;pajc为踝关节中心位置矢量。对于髋关节中心位置矢量phjc,首先以两髂前上棘的中心为基准点,建立骨盆坐标系,其坐标轴单位矢量定义如下
j4=(p1-p2)/|p1-p2|
(3)
(4)
i4=j4×k4
(5)
式中:psacrum=(p3+p4)/2。然后,根据文献[14]给出的线性回归方程确定髋关节中心在骨盆坐标系中的位置,方程如下
(6)
式中:ld表示骨盆深度,为两髂前上棘中点与两髂后上棘中点之间的距离;lw表示骨盆宽度,为两髂前上棘之间的距离。最后,通过坐标变换将髋关节中心从骨盆坐标转换至世界坐标系下表示。
(2)利用关节中心位置坐标和标记点位置坐标确定大腿、小腿和足的局部参考坐标系,所有坐标系原点位于质心位置。以大腿为例,其局部坐标系单位矢量为
k3=(phjc-pkjc)/|phjc-pkjc|
(7)
(8)
j3=k3×i3
(9)
1.2 矢状面关节旋转角度计算
根据解剖学分析,下肢所有关节可视为球关节,包括3个自由度,分别为矢状面的屈、伸,水平面的内收、外展和额状面的内旋、外旋,它们是绕空间转动副转动的三维分量,相互联系协调。考虑下肢行走过程中主要是矢状面运动,而且一般下肢可穿戴机电设备都将髋、膝两个关节的矢状面作为主动驱动自由度,如瑞士的LOKOMAT下肢康复训练机器人、荷兰的LOPES下肢康复训练机器人和日本的HAL助力助行外骨骼机器人等[1,3]。因此,本文重点讨论髋、膝两关节屈、伸角度的识别,结果作为机器人关节驱动的信息源,实现机器人与其使用者的运动同步。
针对1.1小节建立的局部坐标系,定义髋关节屈、伸角θhip为k3在骨盆坐标系矢状面的投影与竖直轴的夹角,定义膝关节屈、伸角θknee为k2在大腿坐标系矢状面的投影与竖直轴的夹角,计算公式为
(10)
(11)

2 表面肌电信号的运动连续解码
2.1 表面肌电信号的采集与活跃强度的提取
根据人体生理学知识,选定肌肉表皮测量位置,利用表面差分电极同步采集行走过程中股直肌、股外侧肌、股内侧肌、股二头肌、半膜肌、腓肠肌外侧、腓肠肌内侧、比目鱼肌、胫骨前肌、胫骨长肌10块主力肌肉的表面肌电信号。
原始表面肌电信号存在噪声干扰,包括设备固有噪声、工频干扰和移动伪迹噪声等。首先利用零滞后的四阶巴特沃斯滤波器对其进行带通滤波,通频带为20~500 Hz,同时进行50 Hz工频陷波,在降噪和伪迹消除的基础上,对信号进行全波整流和低通滤波,得到肌电活跃强度,截止频率为4 Hz。最后,以运动轨迹采集频率对信号进行重采样和归一化处理,得到的表面肌电信号强度时间序列可表示为Xp,q,其中q表示表面肌电信号通道数,p表示采样点数。
2.2 基于DAE的特征降维
特征的选择对模型的学习效率和估计准确性的影响毋庸置疑。文献[4]指出,如果表面肌电信号特征选取得不恰当,会造成信息冗余,另外肌肉活动之间存在一定的相关性,也存在冗余信息。文献[15]提出了一种通过训练多层神经网络进行特征提取和数据降维的深度学习方法,其主要思想是对原始数据进行逐层编码,再逐层解码进行数据重构,当重构数据与原始数据吻合时,那么中间低维空间数据相当于保留了原始数据的全部信息,实现了特征提取和数据降维。相比于PCA方法,深度学习属于非线性变换,通过多层学习能够获得更加本质的特征[16]。本节给出一种基于受限玻尔兹曼机(RBM)的DAE网络,实现多路表面肌电信号强度序列的低维编码,网络拓扑结构如图3所示。

(a)单向预训练网络 (b)双向对称网络图3 基于受限玻尔兹曼机的DAE网络
DAE网络由多个RBM叠加形成,网络的构建与学习可以分为两个步骤:一是通过逐层无监督贪婪学习获得网络的初始参数,称为网络预学习;二是由初学网络参数构造对称结构的双向DAE网络,利用误差反向传播的方法对网络参数进行有监督的学习,称为细调。网络参数预学习解决了传统误差反向传播来训练深度网络时容易陷入局部最优或者产生梯度弥散的问题[15]。误差反向传播方法较为成熟,下面重点论述网络的预学习过程,即RBM学习方法。
RBM是一类具有两层结构,层内无连接、层间全连接的能量模型,且每个神经元只有0或1两种状态,如图4所示。图中h、w和v分别代表隐藏层单元状态向量、连接权值向量和可见层状态向量。RBM在给定一组状态(v,h)后,都有一个标量形式的能量与之对应,其能量函数为
Eδ(v,h)=-aTv-bTh-hTwv
(12)

图4 受限玻尔兹曼机模型
式中:δ=(w,a,b)表示RBM模型参数,其中a和b分别为可见层和隐藏层单元的偏置向量。根据能量函数定义状态(v,h)的联合概率分布函数为
(13)
对于实际问题,我们更关心的是观测数据v的概率分布Pδ(v),即似然函数,具体定义如下
(14)
实质上,RBM学习的任务是求出参数δ,使模型定义的概率分布与观测数据的概率分布一致。参数δ可以通过最大化RBM在给定样本下定义的对数似然函数lnPδ(v)得到,利用随机梯度上升法,参数调整规则如下[17]
(15)
式中:〈·〉data和〈·〉Recon分别表示关于条件概率分布Pδ(h|v)和联合概率分布Pδ(v,h)的数学期望。
由于联合概率分布难以获得,通常采用吉普斯采样计算其近似值,其过程为:首先初始化可见层,然后用条件概率Pδ(h|v)计算隐藏层,再根据条件概率Pδ(v|h)计算可见层,如此循环交替采样k次,可以得到满足RBM定义的联合概率分布样本,最终求得期望。另外,文献[15]提出了RBM的对比分散度快速学习算法,将可见层初始化为样本值,仅进行一次吉普斯采样就能获得很好的效果。在上述采样过程中,需要用到的两个条件分布概率计算公式为
(16)
(17)
式中:f(·)为sigmoid激活函数。
根据上述RBM学习方法,以原始表面肌电信号强度时间序列Xp,q初始化RBM-1的可见层,如图3a所示,通过对比分散度快速学习算法进行训练,然后以RBM-1的输出初始化RBM-2的可见层并进行RBM-2的训练,依次类推进行逐层单独训练,完成DAE所有网络参数的预学习。在此基础上,构造对称结构的DAE网络,如图3b所示,利用误差反向传播的方法对网络参数进行细调,使重构误差最小化[15],即使原始表面肌电信号强度时间序列Xp,q与重构信号XRp,q之间的误差最小。最后获得网络中间层的低维编码Yp,nm,作为原始信号的最优特征矢量。
2.3 基于BP网络的关节角度估计
为确定表面肌电信号特征与关节角度之间的关系模型,建立3层BP神经网络模型,中间层和输出层分别采用正切S型函数和线性函数,如图5所示。
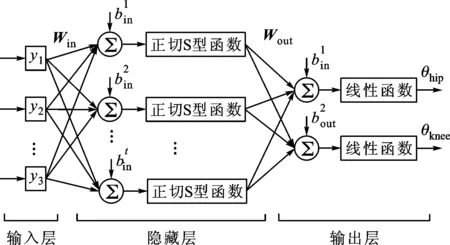
图5 BP网络结构
根据图5可知,BP网络的输出可以表示为
(18)
式中:y=[y1,y2,…,yl]为表面肌电信号特征构成的输入矢量,且l=nm,表示特征维数;θ=[θhip,θknee]为髋关节和膝关节估计角度;Win和Wout分别为隐藏层和输出层的权值矩阵;bin和bout分别为隐藏层和输出层的偏置矩阵。在构建神经网络拓扑结构中,输入神经元和输出神经元个数已经确定,而隐藏层神经元数目采用经验公式确定
t=(l+2)1/2+10
(19)
式中:2表示输出层个数。确定神经网络拓扑结构之后,以深度自动编码网络得到的表面肌电信号最优低维特征值和对应的关节角度为训练样本,采用误差反馈和快速梯度下降方法对网络的权值和偏置进行学习。
3 实验验证
选取4名健康男性对象A、B、C和D(平均年龄为(29±5.5)岁,平均身高为(172±4.3)cm,平均体重为(63.9±5.0)kg)进行步态数据采集,包括标记点运动轨迹和动态表面肌电信号。实验中,测试者被要求在Vicon光学运动捕捉系统工作空间中以不同速度行走(约0.8、1.0和1.2 m/s),12台T40 MX高精度摄像机以120 Hz的频率采集16个标记点在世界坐标系下的位置坐标,配合第三方测试系统(16通道无线生理信号记录仪)同步采集右侧大腿10块主力肌肉的动态表面肌电信号,分别对应1~10个通道,每种步速下得到4组实验数据。实验装置与测试场景见文献[18]。
首先,对所有原始数据进行预处理,包括表面肌电信号活跃度的提取和利用标记点运动轨迹计算关节角度。图6给出测试者A某次行走3 s的关节运动角度,包括了超过两个步态周期的运动,其轨迹曲线变化规律与文献[19]给出的步态数据一致,证明了关节角度计算方法的正确性。在数据预处理的基础上,将所有实验数据分成训练数据和测试数据两部分,即每个部分数据都包括不同速度行走下的2组实验数据,分别用于DAE网络和BP网络的学习与测试。
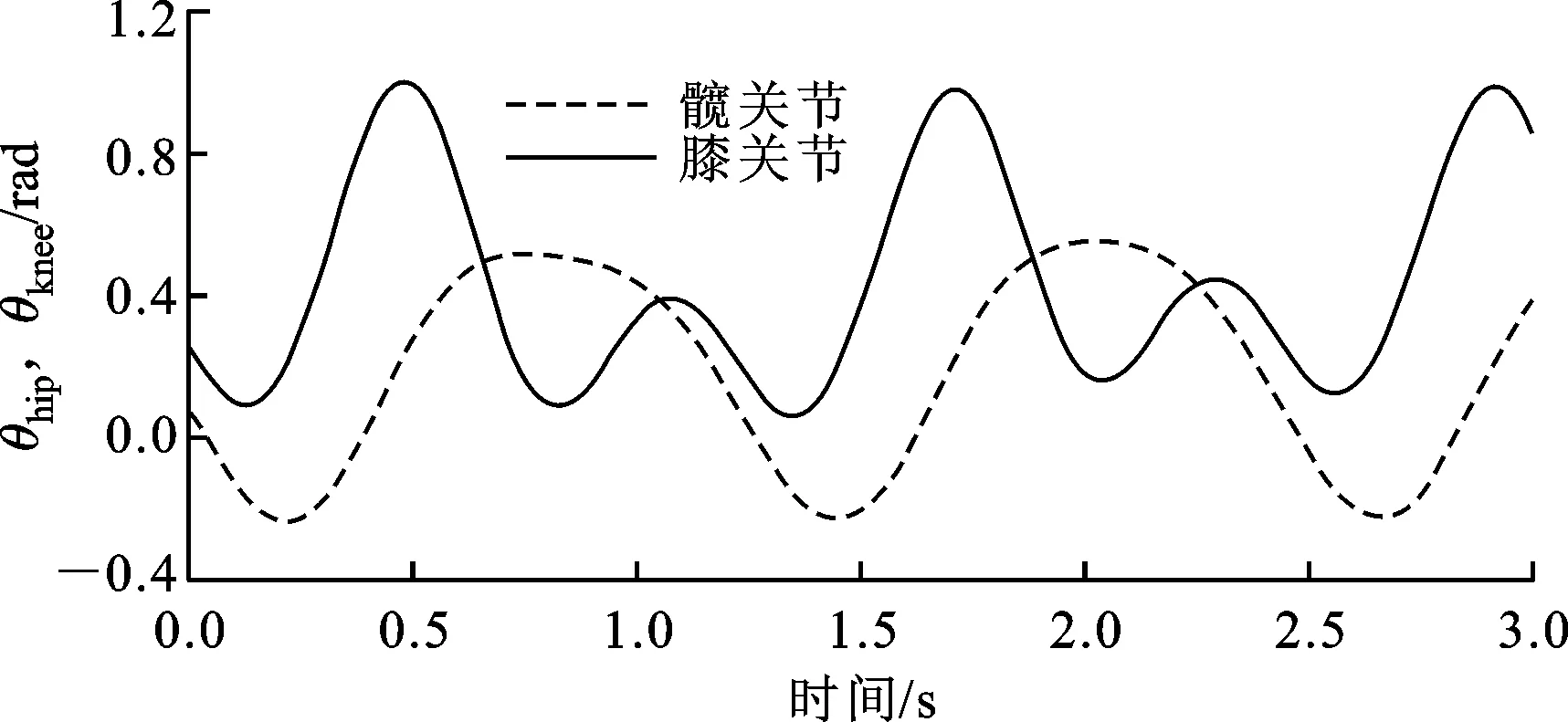
图6 对象A在某次实验下的关节连续运动角度

图7 DAE网络编码原始信号与重构信号对比
其次,构造一个中间层个数为3的9层DAE网络,其中n1、n2、n3、n4和n5分别为10、18、12、6和3,利用训练数据中的表面肌电信号的活跃度信号进行网络的学习,并将学习后的DAE对测试数据中的表面肌电信号活跃度进行自动编码,图7给出了对象A在1.2 m/s行走时肌电强度数据的DAE网络编码结果。对原始数据和重构数据进行比较,两者之间的均方根误差为0.225,即经过DAE网络的多层映射后,其重构信号保留了原始信号的完好信息。图8给出了通过DAE网络和PCA方法得到的低维序列,其中PCA的3个主分量占全部分量的86.7%。由图8可以看出,由DAE网络提取的低维特征信息比PCA方法提取的低维特征信息稳定性更好,尤其是PCA方法得到的第3个分量,其周期性已经变得很差,这势必影响模型的估计精度。另外,为了说明各分量之间的相位关系,图中均以第一维分量中的波峰时刻为参考点标记其余两个分量的对应时刻,可以看出,通过DAE网络提取的三维特征序列之间的相位关系稳定,优于PCA方法得到的结果。

(a)DAE网络降维输出

(b)PCA方法降维输出图8 多路表面肌电信号低维编码序列
最后,通过训练好的DAE网络对所有实验下多路表面肌电信号进行低维编码,同时利用训练数据对BP网络进行学习。图9给出了BP网络模型训练过程中输出的均方误差(η)曲线,由图可知,BP网络快速收敛并稳定,而且利用DAE数据进行训练时,BP网络获得了较高的收敛精度。训练结束后,利用测试数据进行角度估计,图10给出了对象A在1.2 m/s行走速度时的关节角度估计结果,图中同时给出了通过PCA降维数据进行角度估计的结果。从图中可以看出,采用DAE方法获得的表面肌电信号低维特征进行角度估计能够获得更好的效果,尤其是对于变化趋势复杂的膝关节,其估计精度更为明显。此外,利用所有对象的测试结果,计算模型的估计性能指标,如表1所示,具体指标包括均方根误差η和线性相关系数r。通过比较可以看出,通过DAE方法得到的表面肌电信号最优特征作为估计模型输入,模型的估计值与真实值之间的均方误差较PCA方法降低了约25%~35%,线性相关系数也更高。

图9 BP网络训练过程中输出的均方误差曲线

图10 对象A在1.2 m/s行走速度时的关节角度估计结果
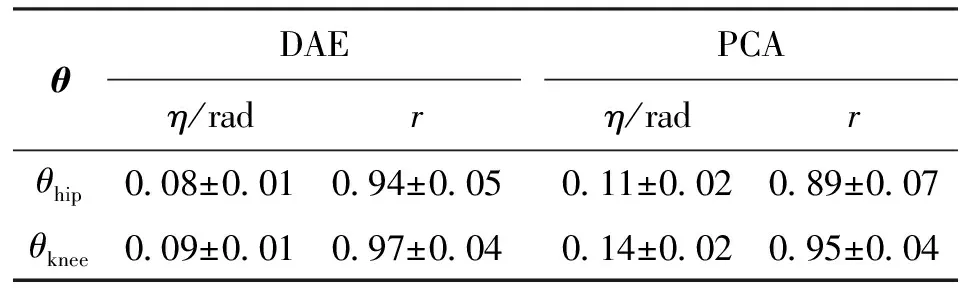
θDAEη/radrPCAη/radrθhip008±001094±005011±002089±007θknee009±001097±004014±002095±004
4 结 论
本文在利用光学运动捕捉下肢步态运动关节角度的基础上,利用多路表面肌电信号实现下肢行走时关节连续运动角度的解码。本文方法特点在于,针对表面肌电信号非线性特点,提出了一种基于RBM架构的DAE网络及其训练方法,实现了多路表面肌电信号的低维编码和最优特征提取,为BP回归模型提供优良的输入数据。人体下肢行走时关节连续运动角度的实验结果证明,与传统的PCA线性降维方法相比,DAE网络对多路表面肌电信号进行多层的非线性映射后,提取的低维特征信息更为全面和稳定,大大提高了BP回归模型对关节运动量的估计精度,统计结果显示模型的估计值与真实值之间的均方误差降低了25%~35%。需要指出的是,本文方法所用的关节运动角度估计模型是通过神经网络回归得到的,文中只针对下肢行走这一特定运动任务下的关节角度进行估计,若要使模型能够适用于更宽的运动任务,只需收集各种运动下的表面肌电信号样本数据进行模型的训练。
[2] 杨启志, 曹电锋, 赵金海. 上肢康复机器人研究现状的分析 [J]. 机器人, 2013, 35(5): 630-640. YANG Qizhi, CAO Dianfeng, ZHAO Jinhai. Analysis on state of the art of upper limb rehabilitation robots [J]. Robot, 2013, 35(5): 630-640.
[3] SANKAI Y. HAL: hybrid assistive limb based on cybernics [M]∥Robotics Research. Berlin, Germany: Springer, 2011: 25-34.
[4] PHINYOMARK A, PHUKPATTARANONT P, LIMSAKUL C. Feature reduction and selection for EMG signal classification [J]. Expert Systems with Applications, 2012, 39(8): 7420-7431.
[5] PHINYOMARK A, QUAINE F, CHARBONNIER S, et al. Feature extraction of the first difference of EMG time series for EMG pattern recognition [J]. Computer Methods and Programs in Biomedicine, 2014, 117(2): 247-256.
[6] TSAI A C, LUH J J, LIN T T. A novel STFT-ranking feature of multi-channel EMG for motion pattern recognition [J]. Expert Systems with Applications, 2015, 42(7): 3327-3341.
[7] LAUER R, SMITH B, BETZ R. Application of a neuro-fuzzy network for gait event detection using electromyography in the child with cerebral palsy [J]. IEEE Transactions on Biomedical Engineering, 2005, 52(9): 1532-1540.
[8] DING Q C, XIONG A B, ZHAO X G, et al. A novel EMG-driven state space model for the estimation of continuous joint movements [C]∥IEEE International Conference on Systems, Man, and Cybernetics. Piscataway, USA: IEEE, 2011: 2891-2897.
[9] ZHANG F, LI P F, HOU Z G, et al. sEMG-based continuous estimation of joint angles of human legs by using BP neural network [J]. Neurocomputing, 2012, 78(1): 139-148.
[10]戴虹, 钱晋武, 张震, 等. GRNN在肌电估计踝关节运动中的应用 [J]. 仪器仪表学报, 2013, 34(4): 845-852. DAI Hong, QIAN Jinwu, ZHANG Zhen, et al. Application of GRNN in ankle movement prediction based on surface electromyography [J]. Chinese Journal of Scientific Instrument, 2013, 34(4): 845-852.
[11]AUNG Y M, AL-JUMAILY A. sEMG based ANN for shoulder angle prediction [J]. Procedia Engineering, 2012, 41: 1009-1015.
[12]丁其川, 赵新刚, 韩建达. 基于肌电信号的上肢多关节连续运动估计 [J]. 机器人, 2014, 36(4): 469-476. DING Qichuan, ZHAO Xingang, HAN Jianda. EMG-based estimation for multi-joint continuous movement of human upper limb [J]. Robot, 2014, 36(4): 469-476.
[13]田国会, 尹建芹, 韩旭, 等. 一种基于关节点信息的人体行为识别新方法 [J]. 机器人, 2014, 36(3): 285-292. TIAN Guohui, YIN Jianqin, HAN Xu, et al. A novel human activity recognition method using joint points information [J]. Robot, 2014, 36(3): 285-292.
[14]HARRINGTON M E, ZAVATSKY A B, LAWSON S E, et al. Prediction of the hip joint centre in adults, children, and patients with cerebral palsy based on magnetic resonance imaging [J]. Journal of Biomechanics, 2007, 40(3): 595-602.
[15]HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks [J]. Science, 2006, 313: 504-507.
[16]余凯, 贾磊, 陈雨强, 等. 深度学习的昨天、今天和明天 [J]. 计算机研究与发展, 2013, 50(9): 1799-1804. YU Kai, JIA Lei, CHEN Yuqiang, et al. Deep learning: yesterday, today, and tomorrow [J]. Journal of Computer Research and Development, 2013, 50(9): 1799-1804.
[17]张春霞, 姬楠楠, 王冠伟. 受限波尔兹曼机 [J]. 工程数学学报, 2015, 32(2): 159-173. ZHANG Chunxia, JI Nannan, WANG Guanwei. Restricted Boltzmann machines [J]. Chinese Journal of Engineering Mathematics, 2015, 32(2): 159-173.
[18]陈江城, 张小栋, 李睿, 等. 利用表面肌电信号的下肢动态关节力矩预测模型 [J]. 西安交通大学学报, 2015, 49(12): 33-36. CHEN Jiangcheng, ZHANG Xiaodong, LI Rui, et al. Prediction model for dynamic joint torque of lower limb with surface EMG [J]. Journal of Xi’an Jiaotong University, 2015, 49(12): 33-36.
[19]TD C, SN G, DJ E, et al. A six degrees-of-freedom marker set for gait analysis: repeatability and comparison with a modified Helen Hayes set [J]. Gait & Posture, 2009, 30(2): 173-180.
(编辑 杜秀杰)
Surface Electromyography Decoding for Continuous Movement of Human Lower Limb During Walking
CHEN Jiangcheng,ZHANG Xiaodong
(Key Laboratory of Education Ministry for Modern Design & Rotor-Bearing System,Xi’an Jiaotong University, Xi’an 710049, China)
To estimate the continuous movement of human lower limb during walking, a regression model which relates the surface electromyography (EMG) and the movement variables of the lower limb joints is constructed. The joint movement angles of lower limb are calculated accurately based on optical motion capture system, then the surface EMG signals are sampled from the main muscles directly concerned with the lower limb motion; the muscle activities are extracted, and a deep auto-encoder (DAE) network with restricted Boltzmann machines (RBM) is realized, by which the multi-channel processed surface EMG signals are encoded in low dimensional space and the optimal features are extracted. The nonlinear model mapping the EMG features to sagittal surface movement angles is established with back propagation (BP) neural network. Extensive experiments indicate that the features extracted with the deep auto-encoder (DAE) network are outperformed principal components analysis (PCA); the movement angles of lower limb joints can be estimated continuously and precisely with the regression models and the mean square error (MSE) between the estimated values and real values is reduced by 25%-35% compared with the traditional method. The proposed strategy is expected to develop human-machine interaction interface technology for the achievement of continuous bioelectric control and the improvement of motion stability between human and machine, especially for lower limb wearable intelligent equipment.
surface electromyography; continuous motion recognition; restricted Boltzmann machines; deep auto-encoder; back propagation network
2015-10-19。 作者简介:陈江城(1987—),男,博士生;张小栋(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金重大研究计划资助项目(91420301)。
时间:2016-03-11
10.7652/xjtuxb201606010
TP242
A
0253-987X(2016)06-0061-07
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160311.1721.010.html

