双重滞后随机前沿模型技术效率的估计

蒋青嬗，韩兆洲

(暨南大学 经济学院， 广东 广州 510632)



【统计理论与方法】

双重滞后随机前沿模型技术效率的估计

蒋青嬗，韩兆洲

(暨南大学 经济学院， 广东 广州 510632)

首次在随机前沿模型中同时引入因变量间(或双边误差间)和技术效率间的空间相关性并构造了双重滞后随机前沿模型，使用极大似然估计方法和JLMS方法得出参数和技术效率的估计。蒙特卡罗模拟表明：忽略技术效率的空间相关性，参数估计和技术效率的估计均表现欠佳。本研究能以较高的精度估计参数和技术效率。随着样本容量的增加，估计效果更优。

随机前沿模型；技术效率；空间滞后；合成误差；极大似然估计

一、引 言

随机前沿分析(SFA)和数据包络分析(DEA)是常见的测算效率的方法，可用来衡量现有技术水平下生产者获得最大产出的能力。数据包络分析属于非参数法，该法最突出的优点是无须具体设定因变量与自变量间的函数关系，从而有效避免了函数形式的误设。但它有几个重大缺陷：首先，它设定了一个确定性前沿，从而不允许测量误差、统计噪声和随机因素等的存在，对奇异值也非常敏感。其次，它不具有统计特性，无法对模型进行统计推断。再者，它适用于静态数据，对动态效率处理欠妥。随机前沿分析能够处理非时变或时变技术效率，而且允许统计噪声、测量误差的存在，有效克服了数据包络分析的不足，在经济、管理等领域应用也越来越广泛。

目前基于随机前沿模型的相关研究已发展的较为成熟。随着时间的延伸，各生产单元技术效率必然会发生改变，Battese等在时变技术效率的情况下研究随机前沿模型并推动了这一领域的发展[1]。Jim分别使用贝叶斯方法估计随机前沿模型[2]。经典的随机前沿模型要求设定函数形式且容易产生模型设定误差，这也是随机前沿模型的缺陷之一。Martins-Filho等研究了半参数随机前沿的估计问题[3]。陶长琪和王志平梳理了随机前沿分析的发展历程及应用，并详细介绍了该法在时变技术效率、异方差、估计方法、外生影响等方面的相关进展[4]。

空间计量经济学是计量经济学的一个分支，该分支认为空间数据存在着空间相依性或空间异质性等空间效应。通过空间滞后项把空间效应引入传统的计量模型，并基于新的模型建立估计、假设检验和统计推断。Anselin总结了空间计量领域近30年来的巨大发展[5]。经典的随机前沿模型假定区域之间或个体之间的独立性，同时还假定区域之间或个体之间的技术效率相互独立。但随着空间计量经济学的发展可知，任何一个地区的经济、生产都不可能独立存在。由于地理位置接近、个体竞争、模仿、溢出效应和测量误差等原因，相邻的经济个体间存在空间相关性。当外生冲击对其经济造成影响时，往往也会波及到邻近地区。强制性使用独立性假设会掩盖空间效应，造成与实际情况不相符合的结论，以此测算出的技术效率也是不可靠的。

归纳相关的空间随机前沿分析文献，目前主要有如下两类空间随机前沿模型：第一，引入因变量滞后项或双边误差滞后项的随机前沿模型。这类模型基于经典的空间自回归模型和空间误差模型。胡晶等分别在随机前沿模型中引入因变量的滞后项和双边误差的滞后项并使用极大似然估计对模型参数和技术效率进行估计[6-7]。类似研究还有林佳显和Zhang等人的研究[8-9]。第二，引入技术效率滞后项的随机前沿模型。Hughes等在对澳大利亚种植产业的产出效率进行实证分析时提出需要考虑技术效率的空间相关性[10]。Areal等对英格兰和威尔士215家乳牛场的技术效率进行实证分析，发现其技术效率也存在明显的空间相关性[11]。技术效率存在明显的空间相关性主要是因为模仿和溢出效应。Agovino、Fusco等也对该类模型做了扩充[12-13]。特别地，目前第二类研究以国外文献居多，目前国内暂无在随机前沿模型中引入技术效率滞后项的研究。

上述文献证实了因变量间(或双边误差间)和技术效率间极可能存在空间相关性。但大部分文献只是单独考虑某种空间相关性，要么只考虑因变量间(或双边误差间)的空间相关性，要么只考虑技术效率间的空间相关性。Anselin指出，当空间相关性确实存在时，忽视空间相关性将导致参数估计有偏和不一致，所得的统计推断也是不可靠的[14]。对于随机前沿模型，当两类空间相关性同时存在时，忽视任意一种空间相关性均将产生模型设定误差并得到有偏和不一致的参数估计，从而以参数估计为基础得出的技术效率估计也是不可靠的。

本文首次在随机前沿模型中同时引入因变量(或双边误差)和技术效率的空间相关性，两类空间相关性是通过两个滞后项引入到模型中，所以简称为双重滞后随机前沿模型。由于模型中引入两类空间相关性，模型本身及其估计变得更加复杂。为得到一致、有效的参数估计，本文对目标模型采用极大似然估计并由一系列数学转化得出该模型的对数似然函数。最后使用JLMS法得到生产单元的技术效率的估计。

二、双重滞后随机前沿模型

(一) 基于空间滞后模型的随机前沿模型

考虑如下随机前沿模型：

Y=ρWY+Xβ+v-u

(1)

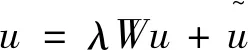
(2)

本研究的模型针对于生产随机前沿模型。式(1)和式(2)构成的随机前沿模型包含因变量和技术无效率项的滞后项，显示因变量间和技术效率间均存在空间相关性。当λ=0，上述模型仅含因变量的滞后项，即为简单的空间自回归随机前沿模型，与胡晶、魏传化和吴喜之提出的模型一致[6]。当ρ=0，上述模型仅含技术无效率项的滞后项，与Areal、Balcombe和Tiffin等提出的模型一致[11]。

对于经典的随机前沿模型，常用的估计方法有修正最小二乘法、广义矩估计法和极大似然估计法。由于复合误差项ε的特殊性，使用普通最小二乘法估计随机前沿模型，斜率系数的估计是无偏和一致的，但截距项的估计却是一致有偏的，所以需要使用修正最小二乘法来修正截距项。广义矩估计和修正最小二乘法虽然操作简单，但同极大似然估计法相比均是无效的。对于空间计量模型，由于空间滞后项的存在，空间模型存在内生性问题，使用最小二乘估计方法得到的参数估计将是有偏且不一致的。常用的估计方法有极大似然估计和广义矩估计。广义矩估计无须误差项满足正态分布的强制性假定，但由于未对空间相关系数施加约束，这导致空间相关系数很可能落在参数空间的取值之外。极大似然估计虽然需要误差项满足正态分布，但由于对数似然函数中包含的雅克比项lnldet(IN-ρw)能很好地把空间相关系数约束在参数空间的取值之内，所以可靠性较佳。基于上述分析，本文使用极大似然估计方法估计上述模型。经过数学变换，上述模型可简化为：

Y=ρWY+Xβ+v-u

(3)

为得到模型(3)的似然函数，需求出复合误差ε=v-u的概率密度函数。易知u和v的密度函数为：

由于v和u相互独立，故其联合密度函数为：

从而u和ε的联合密度函数为：

(4)

令式(4)指数括号内那部分的相反数为Q，即

(5)

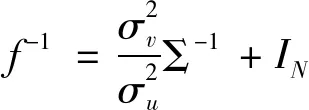
(6)

将式(6)带入式(5)，可得

(7)

将Q带入到u和ε的联合密度函数f(u,ε)，可得：

(8)

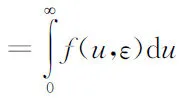
(9)

(10)

(11)

其中Φ(·)是多元标准正态分布的分布函数。从而式(1)、(2)构成的双重滞后随机前沿模型的对数似然函数(已去除常数项)为：

(12)

(二) 基于空间误差模型的随机前沿模型

考虑如下随机前沿模型：

(13)

(14)

(15)

式(13)、(14)和(15)构成的随机前沿模型包含双边误差项和技术无效率项的滞后项，显示双边误差和技术效率均存在空间相关性。当λ=0，上述模型仅含双边误差项的滞后项，即为简单的空间误差随机前沿模型，与胡晶、魏传化和吴喜之提出的模型一致[7]。当ρ=0，上述模型仅含技术无效率项的滞后项，与Areal、Balcombe和Tiffin等提出的模型一致。经过转化，上述模型可简化为[11]：

Y=Xβ+(I-ρW)-1v-u

(16)

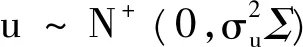
(I-ρW)Y=(I-ρW)Xβ+v-(I-ρW)u

(17)

(18)

转化后的模型(18)同模型(3)类似。可使用类似估计方法，此处不再赘述。

(三) 对数似然函数的转化

极大对数化似然函数可得到参数的估计值。以基于空间滞后模型的双重滞后随机前沿模型为例，其对数似然函数为：

(19)

(20)

从而相应的对数似然函数为：

(21)

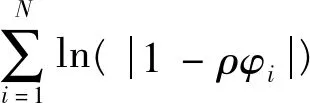
三、技术效率的估计

生产单元的产出与确定性前沿的距离依赖于生产单元技术水平的高低。技术效率用来衡量在现有的技术水平下生产者获得最大产出的能力，生产者的产出能否达到其前沿边界依赖于技术效率。技术效率的估计是随机前沿模型的核心。

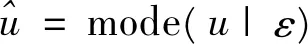
(22)

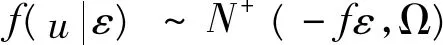
林佳显研究了多元截尾正态分布的均值和众

数。从而本文的众数和均值即为

(23)

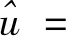
(24)

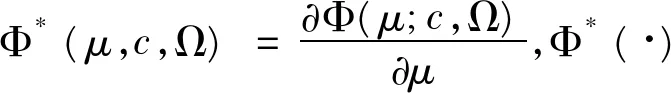
四、蒙特卡罗模拟

针对基于空间滞后模型的双重滞后随机前沿模型进行蒙特卡罗模拟。我们设计如下两组模拟：

模拟(2)。取N=100，其他设定同模拟(1)。比较两组模拟可知，模拟(2)的样本容量大于模拟(1)，这有助于分析大样本下的效果。为凸显文中方法的创新性及适用性，采用两种估计方法进行对比分析：本文提出的方法(即表1中的DLSFM法)和胡晶等人的方法(即表1中的LSFM法)，其中胡晶、魏传化，吴喜之(2011)只考虑了因变量间的空间相关性。基于上述方法的模拟(1)和模拟(2)均模拟100次。

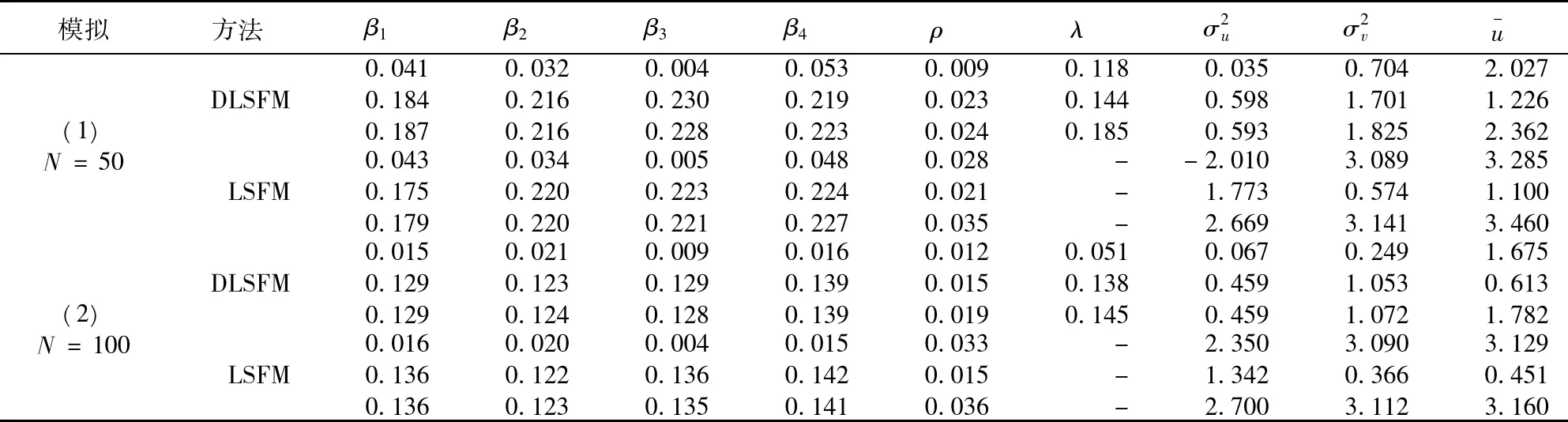
表1 参数估计的精度

上述分析表明，对于模拟(1)和模拟(2)，DLSFM均优于LSFM。综合考虑模拟(1)和模拟(2)，对于DLSFM和LSFM，随着样本容量的增加，大部分参数的偏差、标准差及均方误差相应减少。即随着样本容量的增加，参数估计的效果越好。上述对于模拟(1)和模拟(2)的分析也反映出，随着样本容量的增加，DLSFM中有更多的参数其估计效果优于LSFM，DLSFM和LSFM的估计效果差距变大。综上所述，文中方法对处理双重滞后随机前沿模型有一定的适用性，忽略任一种空间相关性将导致不理想的估计效果。

五、结 论

许多研究证实了因变量间(或双边误差间)和技术效率间极可能存在空间相关性，但现有研究均只在随机前沿模型中考虑一种空间相关性。当两种效应同时存在时，使用现有的模型容易产生模型设定误差，参数估计极可能有偏和不一致，从而以参数估计为基础的技术效率估计也不可靠。本文针对已有模型的不足，首次构造了双重滞后随机前沿模型，该模型能同时捕捉因变量间(或双边误差间)和技术效率间的空间相关性，有效避免了模型设定误差。本文使用极大似然估计和JLMS法分别估计参数和技术效率并使用蒙特卡罗模拟验证估计的效果。

模拟结果表明：(1)忽略技术效率的空间相关性，参数估计和技术效率的估计均表现欠佳。这说明现有模型和估计方法存在不足，双重滞后随机前沿模型存在有必要性。(2)对于双重滞后随机前沿模型，本研究方法在参数估计和技术效率的估计两方面均表现较好。这说明双重滞后随机前沿模型能有效捕捉两类空间相关性，文中估计方法对双重滞后随机前沿模型具有较好的适用性。(3)随着样本容量的增加，该方法的估计效果更优。

本文模型以随机产出前沿模型为基础并用于测算产出效率。稍加转化后也可应用到随机成本前沿模型并测算成本效率。面板数据考虑了空间相关性性和时间依赖性，相对于截面数据模型，面板数据模型的参数估计具有有效性。使用类似的方法也可把文中模型拓展为面板数据模型。

[1]BatteseE,CoelliT.FrontierProductionFunctionsTechnicalEfficiencyandPanelDatawithApplicationtoPaddyFamerinIndia[J].JournalofProductivityAnalysis, 1992(3).

[2]JimE.BayesianStochasticFrontierAnalysisUsingWinBUGS[J].JournalofProductivityAnalysis, 2007(27).

[3]Martins-FilhoC,YaoF.SemiparametricStochasticFrontierEstimationViaProfileLikelihood[J].EconometricReviews, 2015(34).

[4] 陶长琪, 王志平. 随机前沿方法的研究进展与展望[J]. 数量经济技术经济研究, 2011(11).

[5]AnselinL.ThirtyYearsofSpatialEconometrics[J].RegionalScience, 2010(89).

[6] 胡晶, 魏传华, 吴喜之. 基于空间滞后随机前沿模型技术效率的估计[J]. 数理统计与管理, 2011(30).

[7] 胡晶, 魏传华, 吴喜之. 空间误差自相关随机前沿模型及其估计[J]. 统计与信息论坛, 2007(2).

[8] 林佳显. 空间随机前沿模型及技术效率和生产率估计研究[D]. 广州：华南理工大学博士学位论文, 2013.

[9]ZhangJ.ResearchonEstimationofSpatialLagStochasticFrontierModel[J].JournalofBusinessEconomics, 2011(30).

[10]HughesN,LawsonK,DavidsonA,etal.ProductivityPathways:Climate-adjustedProductionFrontiersfortheAustralianBroadacreCroppingIndustry[J].AustralianBureauofAgriculturalandResourceEconomicsandSciences, 2011(2).

[11]ArealF,BalcombeK,TiffinR.IntegratingSpatialDependenceintoStochasticFrontierAnalysis[J].TheAustralianJournalofAgriculturalandResourceEconomics, 2012(4).

[12]AgovinoM.Do“GoodNeighbors”EnhanceRegionalPerformancesinIncludingDisablePeopleintheLaborMarket?ASpatialMarkovChainApproach[J].AnnalsofRegionalScience, 2014(1).

[13]FuscoE,VidoliF.SpatialStochasticFrontierModels:ControllingSpatialGlobalandLocalHeterogeneity[J].InternationalReviewofAppliedEconomics, 2013(27).

[14]AnselinL.SpatialEffectsinEconometricPracticeinEnvironmentalandResourceEconomics[J].AmericanJournalofAgriculturalEconomics, 2001(3).

[15]JondrowJ,LovellK,MaterovI,etal.OntheEstimationofTechnicalInefficiencyintheStochasticFrontierProductionFunctionModel[J].JournalofEconometrics, 1982(19).

(责任编辑：李 勤)

The Estimation of Technical Efficiency based on Double-lag Stochastic Frontier Model

JINAG Qing-shan, HAN Zhao-zhou

(Economic College, Jinan University, Guangzhou 510632, China)

This article simultaneously incorporates spatial dependent of dependent variables (or two-sided error) and technical efficiency for the first time and then structures double-lag stochastic frontier model. We use maximum likelihood estimation and JLMS method to get the efficient estimation of parameters and technical efficiency respectively. The numerical simulation shows that: when neglect the spatial dependences of technical efficiency, the related estimations have poor performance. The method in this article does well in the estimation of parameters and technical efficiency. With sample size increasing, the two aspects can do better.

stochastic frontier model； technical efficiency； spatial lag； composite error； maximum likelihood estimation

2016-03-25

广东省委宣传部打造“理论粤军”2014年度重点课题《广东经济监测与预测研究》(WT1407)

蒋青嬗，女，湖南衡阳人，博士生，研究方向：统计信息与决策支持系统研究； 韩兆洲，男，江苏苏州人，经济学博士，教授，博士生导师，研究方向：统计信息与决策支持系统研究。

O212∶O242.2

A

1007-3116(2016)11-0038-07