多轴联动系统动态特性建模及仿真

赵志明，曾书琴，薛莹洁

（陕西科技大学 机电工程学院，西安 710021）

多轴联动系统动态特性建模及仿真

赵志明，曾书琴，薛莹洁

（陕西科技大学 机电工程学院，西安 710021）

在飞行器研制过程中，多轴联动系统性能的优劣直接影响航空、航天产品的精度，因此利用计算机对转台进行动态仿真很有必要。在SolidWorks中对二轴转台进行了三维建模，并建立相应的运动方程；基于ADAMS动力学仿真软件，对二轴转台的方位轴和俯仰轴进行动力学分析。通过仿真模拟，得到了内外框单独运动时和耦合运动时的运动曲线和电机的转矩输出曲线。对比分析不同情况下内外框的运动曲线及驱动电机转矩输出情况，为电机选择和转台的结构设计及优化提供参考。

二轴转台；仿真；动力学

0　引言

随着光学电子和航空技术领域快速发展，多轴仿真转台凭借其体积小、重量轻、成本低、稳定度高等优点，被广泛应用于军事及民用领域中。由于多轴仿真转台负载要求，多轴仿真转台的重量、体积、机电耦合，直接影响了整个系统的性能。因此，探究仿真转台的结构和动力学特性具有重要意义。本文以二轴仿真转台机构设计和动力学分析为例进行研究。

1　二轴仿真转台的选型

多轴仿真转台[1]能够模拟导弹、飞行器的实际飞行条件，它与目标仿真装置组合在一起就能模拟出导弹和被袭目标的运动性能，是测试导引头性能的重要设备[2]。其框架的结构型式直接影响了多轴转台的整体结构设计、承载能力等。二轴转台由两个相互垂直的框架构成，结构型式有立式和卧式，两框的组合型式有U-O，O-O，U-T等[3]。本文根据二轴转台的体积、重量、控制精度及挂载方式的要求选择立式U-O型，如图1所示。其优点一是前方和上方是敞开的，不存在盲区，便于装卸和观察被测件；二是当转台实现方位和俯仰运动使框架处在不同位置时，框架自身重力引起的静态变形的差别不大，这一点对设计高精度仿真转台有利[4]。其主要缺点是外框架的动态刚度偏低，为此也可将外框设计成封闭的O型结构，在其上方也设置支承，但转台的高度和外形尺寸将增大。本文设计的二轴仿真转台包括内俯仰框架和外方位框架，内框绕俯仰轴Y轴摆动，外框绕Z轴摆动，其运动方程均为正弦函数。俯仰轴与方位轴相互独立且正交。

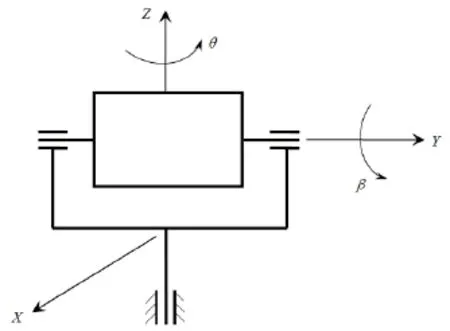
图1　二轴转台结构示意图

2　二轴转台运动方程的建立

内、外框架的运动由直流无刷力矩电机直接驱动[5]，分别绕俯仰轴Y轴、方位轴Z轴摆动，完成方位的调整。作用在两个框架上的力矩主要为：作用在刚体上的外加力矩、刚体本身和负载的重力力矩、各刚体间的约束力矩和摩擦力矩。

2.1坐标系的建立

根据二轴转台的结构定义其坐标系如图2所示，设二框架交于固定点O点，O-XYZ为惯性坐标系；O-XoYoZo、O-XiYiZi分别为外框、内框坐标系，并分别绕OZo、OYi转动，转角分别为θ、β。二轴转台由两个活动的刚体组成，其动力耦合与转矩耦合经过θ、β旋转后，设内框某点在惯性坐标系O-XYZ的坐标为(xp,yp,zp)T,在新的坐标系O-XiYiZi的坐标为(x,y,z)T，则有：

外框绕Z轴摆动的角速度矢量为：

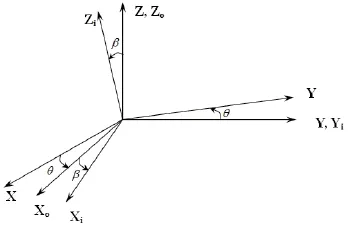
图2　二轴转台绕轴转动的坐标系

2.2各框运动方程式的建立

各框的转动惯量表示如下：外框绕Zo，Yo，Xo轴旋转的转动惯量分别为Jzo，Jyo，Jxo；内框绕Zi，Yi，Xi轴旋转的转动惯量分别为Jzi，Jyi，Jxi。假设各框架均相对于各自坐标系是对称的，即：

由于刚体绕定轴转动时，其转动力矩为动量对时间的导数，因此：

内框在外框上的转矩的投影为：

其中Jxi=1.6kgm2，Jyi=1.18kgm2，Jzi=1.47kgm2；JzO=9.61kgm2，JyO=7.99kgm2，JzO=9.61kgm2。

3　基于ADAMS运动学分析和动力学分析

3.1简化模型建立

利用ADAMS软件建立模型时，可以通过其自身图形库对模型建立，也可以通过其他三维软件建模后导入。本文模型较复杂，所以使用SolidWorks软件建立模型后，另存为*.x_t格式文件后导入ADAMS中。导入模型之前，在不影响总体结构仿真的前提下还需进行对模型的简化[6]。简化的主要思路是将各框及其附属部件视为一个整体的PART进行简化，然后将各简化部分再组合。导入后的完整模型如图3所示。

图3　二轴转台的仿真模型

3.2约束的添加

模型简化和导入后，根据各零件间相对位置关系添加约束，本文在内框轴和外框架间建立旋转副JOINT_13，并添加驱动MOTION_1，负载和内框固联以提供载荷，因此无需添加负载力；在外框和基座之间建立旋转副JOINT_14，并添加驱动MOTION_2，基座和大地固联。

3.3二轴仿真转台运动仿真及耦合分析

为了了解二轴转台运动情况以及运动时各框架输出力矩，分别分析二轴转台内外框单独运动时的角速度、角加速度及输出力矩情况和内外框共同运动时角速度、角加速度及的输出力矩情况。约定其角速度为300°/s，角加速度为50°/s2。则电机函数为θ=1800×sin(1/6d×time)，设置仿真条件ENDTIME：2160，STEPS：100。

1）设置内框运动MOTION_1=1800×sin(1/6d×time)，MOTION_2=0。内框的角速度、角加速度及输出力矩（Y方向）如图4所示。此时内框的角速度为300°/s，角加速度的最大幅值为0.8°/s2，输出力矩的最大幅值为0.018N.m，以正弦规律变化。

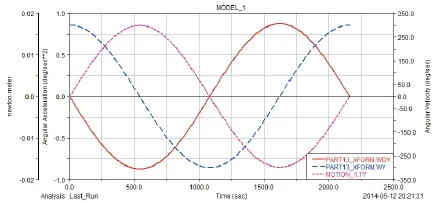
图4　内框的运动学曲线

2）设置内框运动MOTION_2=1800×sin(1/6d×time)，MOTION_1=0。外框的角速度、角加速度及输出力矩（Z方向）如图5所示。此时外框的角速度和角加速度和内框的相同，但输出力矩的最大幅值为0.048N.m，也以正弦规律变化。

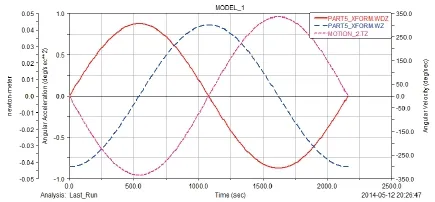
图5　外框的运动学曲线

3）内外框电机均设置运动θ=1800×sin(1/6d×time)，内外框耦合运动时的动力学图线如图6和图7所示。

图6　耦合运动时内框的运动学曲线

此时，内框的三个参量均未按标准的正弦规律变化，但角速度的最大幅值仍为300°/s，角加速度的最大幅值增加至1000°/s2之多，输出力矩最大幅值增加至2.4N.m，增加约133倍；外框的角速度和角加速度均没有收到影响，输出力矩最大幅值增大至5N.m，增大约104倍。

图7　耦合运动时外框的运动学曲线

4　结论

通过对比两种情况下的运动学曲线，可以得到在内外框耦合运动时，对内框电机的输出转矩影响很大，对其运动性能也有很大影响；而对外框的电机输出转矩影响相对较小，对外框的运动性能几乎没有影响。所以，当内外框同时以较高速度运动时会引起各框架件的力矩耦合，对内框的电机输出转矩影响最大，因此在控制系统中，要采取有效的解耦补偿措施，否则将难以达到系统的精度和动态跟踪精度。

本论文通过对二轴转台的选型、建模和各框架的运动学方程的建立，利用ADAMS软件对其进行运动学分析，分析表明，当各框架同时以较高加速度运动时，会引起各环框架间的力矩耦合，对内框俯仰轴电机输出转矩的影响较大，对外框电机的输出转矩影响较小。

[1] Qiaosheng Liu a, Juntong Xi. Case-based parametric design system for test turntable[J].Expert Systems with Applications, 2011,38：6508-6516.

[2] 梅晓榕,陈明,张卯瑞.三轴仿真转台的建模与仿真[J].系统仿真学报,2001,13(3)：278-279.

[3] 张先彤,张庆春,陈时锦,等.OUT型闭式三轴转台的结构设计[J].中国惯性技术学报,1996,4(2)：58-60.

[4] 孙伟,车莉娜,徐爱功.三轴惯性仿真转台的动态性能测试方法[J].压电与声光,2013,35(4)：520-521.

[5] 崔广志.电动三轴仿真转台控制系统研究[D].哈尔滨工业大学,2007.

[6] 王晶东,于化东,许金凯,等.两轴三框架光电稳定平台动力学分析[J].机械设计与研究,2013,29(4)：33-35.

Dynamics modeling and simulation of multi-axis system

ZHAO Zhi-ming, ZENG Shu-qin, XUE Ying-jie

TH745

A

1009-0134(2016)07-0076-04

2015-12-01

国家自然科学基金（51305246）；陕西科技大学博士启动基金（BJ13-07）；陕西省教育厅专项研究（14JK1107）

赵志明（1981 -），男，山东威海人，讲师，工学博士，研究方向为转子动力学、运动控制和旋转机械故障诊断。