探解题方法 悟价值取向
——基于一道中考试题的分析
王竞进
探解题方法 悟价值取向
——基于一道中考试题的分析
王竞进
对于一道高质量的中考试题,教师既要引导学生运用所学知识探求试题的解法,又要挖掘试题背后所隐含的教学价值。教师在平时的教学中要以试题或例题为载体,使得解题教学从纯粹的学习解题方法走向学习学科思维,促进学生数学核心素养的形成。
例题教学;解法分析;运算能力;价值取向
一道高质量的中考试题,能够反映出命题者对数学知识内容的深度领悟、对数学本质的准确把握以及对今后教学工作的期待和导向。有研究者提出,衡量中考数学试题质量的高低,首先是看在符合中考性质的前提下,其试题立意的高低。试题的基本价值立场、价值态度以及所表现出来的基本价值倾向和对教学的引导与促进作用就是试题的价值取向。笔者以为2016年江苏省盐城市中考数学试题第18题就是一道高质量的试题,本题无论在知识立意还是能力考查方面,都充分体现了命题者对数学知识的整体把握和对今后教学工作的导向。本文试以此题为例,探究不同的解答方法,感悟其蕴含的价值取向。
一、试题呈现
如图1,已知菱形ABCD的边长为2,∠A=60°,点E、F分别在边AB、AD上。若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF=_______。
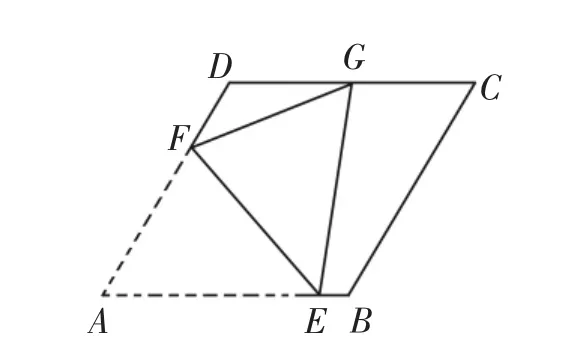
图1
二、试题解答探究
本题的图形中是否隐含着基本图形呢?由于四边形ABCD是菱形且∠A=60°,因此,其中隐含着两个等边三角形,分别为△ABD和△BCD。同时,图形中的△AEF与△CEF是关于EF折叠,因此AG必定被折线EF垂直平分,点O为线段AG的中点,因此,利用图形的性质构造分别含有线段EO和FO的两个三角形相似,便可求得其长度,因此,得到如下解法。
【解法一】如图2,连接BG、AG、BD,过点G作GH⊥AD,垂足为H。设AG、BF交于点O。
因为四边形ABCD是菱形,所以AB∥CD,BC= CD。
因为∠A=60°,所以∠C=60°,所以△BCD是等边三角形。
因为点G是边CD的中点,所以∠BGC=90°,∠ABG=90°。


除了上述的解法一外,是否还有其他解法呢?由于图形中的△AEF与△GEF是关于EF折叠,因此AG必定被折线EF垂直平分,即四边形AEGF的对角线互相垂直,由菱形的面积等于对角线乘积的一半,可以联想到类推对角线互相垂直的四边形面积也等于对角线乘积的一半,因而从图形面积的等积角度展开探索,得到了如下的解法。
【解法二】如图2,连接BG、AG、BD,过点G作GH⊥AD,垂足为H。设AG、BF交于点O。
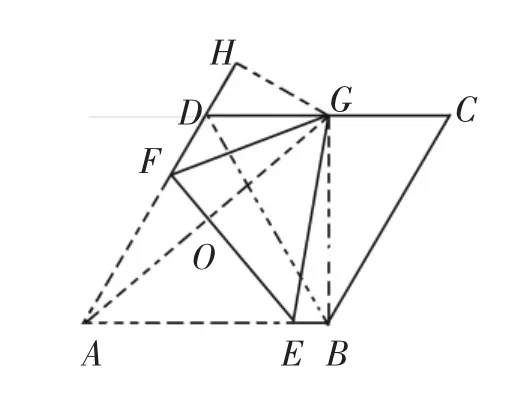
图2
因为四边形ABCD是菱形,所以AB∥CD,BC= CD。
因为∠A=60°,所以∠C=60°,所以△BCD是等边三角形。
因为点G是边CD的中点,所以∠BGC=90°。
因为△AEF与△GEF是关于 EF折叠的,△AEF≌△GEF,所以AE=EG,AF=FG。
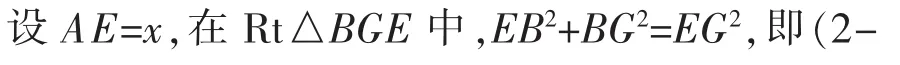

解法一与解法二都是利用隐含的线段BG与边CD垂直关系,分别构造相似的两对三角形求得边长以及应用勾股定理求得线段长。能否直接以线段EF为直角三角形的边进行入手呢?因此,沿着这样的思路,得到了如下的解法。
【解法三】如图3,连接BG、AG、BD,过点F作FH⊥AB,垂足为H,交CD延长线于点I。
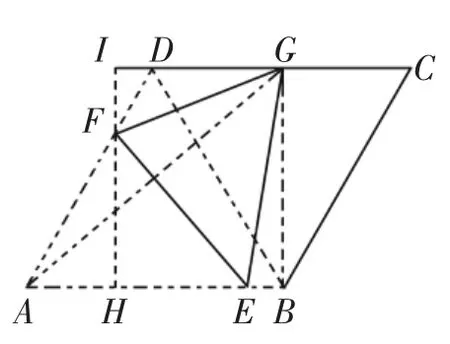
图3
因为四边形ABCD是菱形,∠A=60°,所以∠IDF=60°,DF=2DI,FI=
同方法二,可得AF=FG。设DI=x,则DF=2x,FI=
Rt△GFI中,IF2+GI2=FG2,即解得即AF=FG=2-2x=
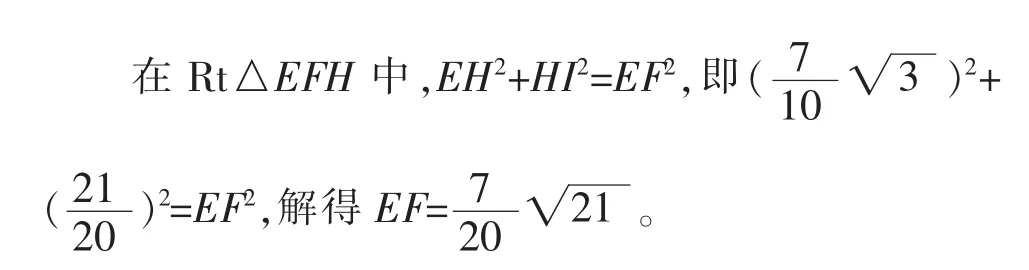
当然,如果将菱形ABCD放到平面直角坐标系内,那么图形中的点B、C、D、G的坐标都是确定的,因此,图形中的点E、F的坐标也是确定的,则线段EF的长度也是确定的,由此可以得到了基于坐标系的第四种解法。(具体过程略)
三、教学价值取向分析
首先,重视课本例题、习题的教学。
本题源于苏科版《数学》八年级下册第95页第21题:在矩形纸片ABCD中,AB=6,BC=8。
(1)将矩形纸片沿BD折叠,点A落在点E处(如图4-①),设DE与BC相交于点F,求BF的长;
(2)将矩形纸片折叠,使点B与点D重合(如图4-②),求折痕GH的长。
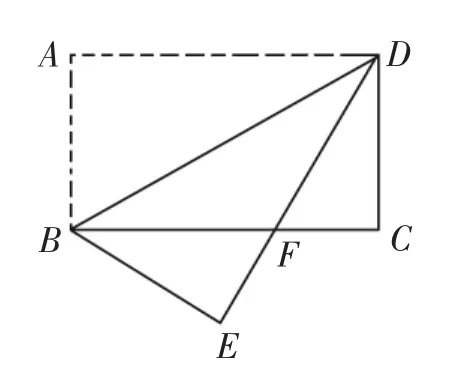
图4-①
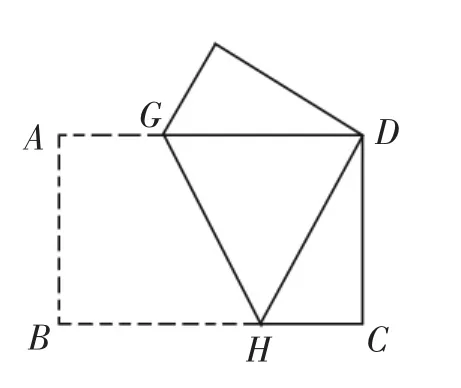
图4-②
本题较好地体现了命题设计源于课本又高于课本的理念,本题的设计重心落脚在考查学生对特殊平行四边形的性质、等边三角形的性质、图形变换的性质、图形的全等、相似和勾股定理等知识的掌握,同时考查了学生运算能力和方程思想的运用。因此,在平时的教学中,我们要重视教材中典型例题和习题的应用,灵活地以课本习题为母题进行深入研究、适度的演变、引申和拓展,科学地引导学生进行探究、分析、总结、发展,以巩固基础知识的掌握、基本技能的形成。
其次,重视基本图形的积累教学。
一道综合题中往往都蕴含着一个或几个简单的基本图形,只要平时加强基本图形的教学,掌握好基本图形及其性质,能从复杂图形中分离出基本图形,再从基本图形出发进行推理,由基本图形的类比、变化中得到解题思路,从而实现复杂图形的基本化。本题的解法尽管并不唯一,但他们都抓住了图形中的基本图形,因而出现了从不同的思维角度解决问题的策略。解法一,能够根据菱形ABCD中∠A=60°,联想到图形中隐含着两个等边三角形,并从等边三角形的性质、轴对称图形的性质入手,构造了两对三角形相似求得线段长;解法二,根据图形中隐含的四边形对角线互相垂直,联想到由菱形的面积公式,并类推其面积也等于对角线乘积的一半,再从图形面积相等这一角度展开探索求得结果;解法三,直接以所求线段为直角三角形的斜边构造直角三角形,以直角三角形为基本图形展开探求对应线段长的过程;解法四,能够根据图形的特征将其放到平面直角坐标系内,得到图形中的相应点的坐标、直线的函数表达式,因此,抓住图形中的基本点E、F的坐标求得线段EF的长度。
最后,重视学生运算能力的培养。
从考生考后反馈的信息来看,不少学生认为本题的解题思路有了,但由于自己的计算基本功不扎实,而导致没有能够求得正确的结果。《义务教育数学课程标准(2011年版)》强调:“在数学课程中,应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。”“在‘数与代数’的教学中,应帮助学生建立数感和符号意识,发展运算能力和推理能力,初步形成模型思想。”因此,运算能力是数学课程标准所提出的核心素养之一,平时的教学不可忽视,更不能以“运算耽误时间”“影响思考时间”而降低运算能力的培养。教学中,我们要让学生养成计算步步有根据、有充足的理由的习惯,提醒学生注意运算的顺序,提高运算的简捷性。
[1]左坤.中考数学试题的价值取向[J].中学数学教学参考:中旬,2010(12).
[2]董林伟.义务教育教科书·数学八年级下册[M].南京:江苏科技出版社,2014.
[3]中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
G633.6
A
1005-6009(2016)54-0034-03
王竞进,江苏省建湖县汇文实验初中教育集团(江苏建湖,224000)教师,高级教师,盐城市学科带头人。

