破茧成蝶，让学习真正发生——以“等比数列前n项和”教学为例

孙岚

破茧成蝶，让学习真正发生
——以“等比数列前n项和”教学为例

孙岚

用适合的方案、适当的问题、适时的跟进和适宜的题型来引导学生研究性地进行学习，从而把学习当成自己的事，这才是真正的学习。本文就“等比数列前n项和”的教学设计谈谈对“让学习真正发生”的理解。

等比数列前n项和；教学设计；高中数学

在种类繁多的蛾子中，有一种叫“帝王蛾”，它的幼虫生长在茧中，要变成蛾时它必须拼尽全力往外冲，由于洞口过于狭小，不计其数的蛾子悲壮倒下。有人不忍看到这惨烈的一幕，便将洞口剪大，让幼虫可以轻而易举地钻出那可怕的牢笼，但这些没有经历过“冲杀”的蛾子，却永远与飞翔无缘，永远也无法成为真正的帝王蛾。帝王蛾如此，学生亦然，没有经历探究的过程而直接传授结论，就不会让能力有所提升。所以课堂上教师的作用是让学生看到“茧外世界的美好”，激发他们“破茧”的欲望，点拨他们“破茧”的方法，用适合的方案、适当的问题、适时的跟进和适宜的题型来引导学生研究性地进行学习，把学习当成自己的事，这样才能让学习真正发生。笔者以“等比数列前n项和”的教学设计为例，谈谈如何做到“让学习真正发生”。

一、给学生创设一个适宜学习的情境

实践证明，学生在不平等的环境中的学习是被动的、紧张的、不愉快的。学生也容易产生厌学心理。因此，教师应对学生抱以期盼和希望，让学生在宽松和谐的学习氛围中找到自己，自主进行学习。

《普通高中数学课程标准（实验）》中指出：教材应注意创设情境，从具体事例出发，展现数学知识发生、发展的过程，使学生能够从中发现问题、提出问题，经历数学的发现和创造过程，了解知识的来龙去脉。那么什么样的情境才能让学生有探索新知的欲望，才能使师生处于平等的位置，让学生主动、轻松地学习呢？

我是这么教学的——

师：大家好，这节课我们一起来做个游戏，现在我来分配一下角色，你们是印度的国王，我是国际象棋的发明者。我想向您请求一些赏赐，赏赐的条件是，在国际象棋棋盘的第一个格子里放一粒麦子，第二个格子里放2粒麦子，第三个格子里放4粒麦子，第4个格子里放8粒麦子，以此类推，后一个格子里的麦粒数是前一个格子麦粒数的2倍。国王陛下，您能把这样放满整个棋盘64个格子的所有麦粒都赏赐给我吗？

（学生在思考，没有应答）

师：这是一个什么数学问题？

生：等比数列。

师：哪句话体现了这是一个等比数列？

生：后一个格子里的麦粒数是前一个格子麦粒数的2倍。

师：那么等比数列的定义是什么？通项怎么表示？有几个基本量？

角色扮演式的课堂引入，让学生体验到新鲜感，在一定程度上体现学生在学习上的主体地位。此外，问题设计的起点较低，每个学生都能做出对应的回答，增强了他们后续学习的信心。学生具备了探索的欲望，何愁他们会不认真学习呢？

二、让学生找到通往新知的阶梯

美国心理学家布鲁纳认为：“知识的获得是一个主动的过程，学习者不应是信息的被动接受者，而应是知识获得过程中的主动参与者。”所谓“授人以鱼，不如授人以渔”，优良学习方法、思维方法的习得，会让学生的学习变得更有效、更深入。本节课的难点是等比数列前n项和公式的推导，在教学中教师应当引导学生逐步发现、运用错位相减法进行数列求和，并使之内化为学生认知结构的一部分，而不仅仅是生搬硬套的结论。继续上面的游戏——

师：“国王陛下，您能把这样放满整个棋盘64个格子的所有麦粒都赏赐给我吗？”这又是一个什么数学问题？

生：等比数列前n项和。

师：能算出来是多少吗？

生：项数太多了，死算算不出来。

师：那么你们之前有遇到过类似的问题吗？

生：等差数列前n项和。

师：当时我们是采用什么方法解决？

生：倒序相加。

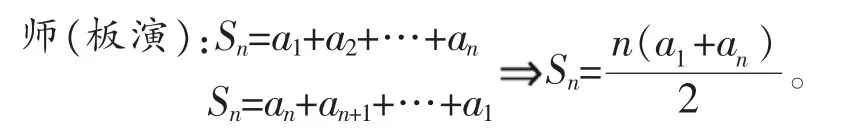
类比等差数列前n项和，对于等比数列的前n项和我们能否找到一个有效的手段来消项？

生：也用倒序相加。

师：试试看，是否可行。

学生（尝试1分钟后）：不可以，不能进行消项。

师：那怎么办呢？等比数列项与项之间的联系到底在哪里呢？

生：后一项与前一项的比值是一个定值。

师：很好，请大家围绕等比数列的这一定义，目标是消项，寻求基本量的最简形式，探求等比数列的前n项和，我给大家3分钟的时间，可以尝试不同方法。

师追问：怎么想到乘以q，乘q之后有何好处？

生1：考虑到等比数列的定义，后一项等于前一项乘以公比q，乘q之后产生了很多公共的项，作差就达到了“消项”的目的。

师：很好，你来具体说说。

上面式子的第2项和下面式子的第1项相同，上面式子的第3项和下面式子的第2项相同……，上面式子的最后一项和下面式子的倒数第二项相同。作差得，(1-q)Sn=a1-anq，即

师：q=1时呢？

生1：每一项都相同，等于a1，所以Sn=na1。

师：能不能总结一下求解的基本步骤？

生1：乘以公比，错位，相减，化简。

师：总结的非常到位，所以我们可以给它命名为？

生：错位相减法。

知识的习得是一个螺旋上升的过程，很多新旧知识之间存在一种“温故而知新”的关系，教师不是急于给出结果，而是起到一个穿针引线，搭建一条连接新旧知识阶梯的作用。通过与等差数列求和方法的类比，把求和的计算转化到如何进行“消项”。学生在自己的自主探究与教师的引导中，感悟更加清晰，思维更加深刻。这也有力地说明了教学活动不能直接灌输，而应该在学生的活动与思考后加以点拨，这样的设计使学生在理解和接受数学思想方法层面上是科学和自然的，给学生一种水到渠成之感。

三、为学生搭建思维共鸣的舞台

著名数学家斯托伊亚尔指出：“数学教学是数学活动（思维过程）的教学，而不是数学结果（数学知识）的教学。”可见，思维过程是教学的核心，数学教育应着眼于培养学生终身发展的能力，我们的课堂应着力于提升学生的核心素养，因此，不讲思路和过程，忽视思想和方法，将结论硬塞给学生，无疑会抑制学生的探索、创新能力，阻碍学生的思维发展。那么如何才能培养学生的思维能力，使学生得到终身发展呢？这就要求教师在课堂上不能以 “教”代“学”，而是要让学生经历发现、收集、理解这一学习的过程。

等比数列公式的推导是本节课的重点和难点，如何想到错位相减这一方法也是本节课要突破的关键点，要突破这些教学难点不是一问一答就能完全解决的，而是要通过几个环节的跟进，让更多的学生思考得更充分、更深入。通过学生思维的交流捕捉学生想法中的闪光点和值得商榷的地方。在类比等差数列求和方法的时候，学生在交流时发现求和的关键是消项，于是提出了也用倒序相加的方法对等比数列进行消项，教师并没有急于否定，而是让学生自己尝试，在探究中发现消项的关键是观察项与项之间的联系，在矛盾冲突中让学生的思维不断碰撞，得出项与项的联系就在于后一项等于前一项乘以公比，从而让学生自己找出等比数列的求和方法，比如，有学生指出可以根据定义：a2=a1q，a3=a2q，a4=a3q，…，an=an-1q。累加得：Sn-a1=q（Sn-an）化简得：当q≠1时

这样教师把问题抛给学生，让学生自己思考，在亦退亦进间，让学生经历了思维的冲击，开阔了视野，享受了学习的过程。让学习真正发生，教师的作用就在于构建一个让学生学习、经历的“有意义”的过程，使他们在过程体验中理解和把握知识，从而形成自己的知识网络，更重要的是形成自己的“思想”，最终从认识走向求知，从有形走向无形，从单一走向立体。

如果说“授人以鱼，不如授人以渔”，那么我觉得，授人以渔，必先授人以欲。课堂教学中，我们要做的不是为学生“剪开洞口”，而是通过对学生的学习过程进行组织和调整来激发学生的欲望，锻炼他们的技能，让他们形成“破茧”的能力。让他们通过自己的思考、交流、探索生成属于自己的知识，进而培养他们的习惯、提升他们的能力、从而内化成自身的素质。我们要培养的不是被抱出洞口的孱弱的“虫子”，而是蜕变出强有力翅膀的“帝王蛾”。

［1］谢丽丽，杨光伟.激活思维，“生动”课堂——“等比数列前n项和”教学研探［J］.中学教研，2014（06）.

［2］王斌.展示思维过程提高思辨能力［J］.宁德师专学报：自然科学，2007（03）.

［3］张金平.建构“有意义”的学习经历［J］.江苏教育：小学教学，2016（01）.

G633.6

A

1005-6009（2016）54-0032-02

孙岚，江苏省沙溪高级中学（江苏太仓，215421）教师，一级教师。