复合材料薄壁轴转子系统动力学特性的有限元分析

仲惟燕，任勇生，高 峰，刘 蕾，刘 洁

(1.山东科技大学 机械电子工程学院，山东 青岛 266590；2.城发投资集团有限公司，山东 青岛 266555；3.山东科技大学 电气信息系，山东 济南 250031)



复合材料薄壁轴转子系统动力学特性的有限元分析

仲惟燕1，任勇生1，高 峰1，刘 蕾2，刘 洁3

(1.山东科技大学 机械电子工程学院，山东 青岛 266590；2.城发投资集团有限公司，山东 青岛 266555；3.山东科技大学 电气信息系，山东 济南 250031)

采用有限元软件ANSYS建立了复合材料薄壁轴的有限元模型，通过模态分析得到系统的固有频率和临界转速，将结果与相关文献的结果进行比较，说明了模型的正确性。然后建立了包含轴承、转盘在内的复合材料薄壁轴转子系统的有限元模型，研究了转子系统的动力学特性。讨论了复合材料铺层角度、铺层顺序、长径比、轴承刚度和转盘安装位置等因素对转子系统固有频率和临界转速的影响，随后分析了转盘质量、转盘安装位置、轴承刚度和轴承阻尼对转子系统不平衡响应的影响。该分析方法为复合材料薄壁轴转子系统的动力学研究与设计，提供一种可供选择的分析方法。

复合材料；薄壁轴；固有频率；临界转速；不平衡响应

随着工业技术的进步，旋转机械变得越来越大，运行速度也越来越高[1]。由于具有高强度、高刚度、低密度的特点，复合材料已广泛用于旋转机械部件的设计，例如直升机尾传动轴、汽车传动轴以及喷气发动机的传动轴。国内外学者已经提出了复合材料传动轴的一些动力学模型，并对其进行分析研究。Zinberg等[2]较早介绍了复合材料传动轴在直升机上的应用，他们利用等效模量梁理论对复合材料轴进行了动力学建模，对临界转速的理论结果与实验结果进行了对比。Bert等[3]基于Bresse-Timoshenko梁理论并考虑陀螺效应推导了复合材料传动轴的动力学方程。Singh等[4]分别应用等效模量梁理论和分层梁理论建立了复合材料轴的动力学模型，研究发现对于不对称铺层的复合材料传动轴，两种模型求得的临界转速存在偏差。El Mahdy等[5]对单向纤维增强复合材料与传统材料转子的自由振动特性进行了比较。Chang等[6]基于一阶剪切梁理论建立了轴承支承的复合材料轴盘系统的有限元动力学模型。Gubran等[7]提出了考虑铺层顺序和耦合影响的修正的等效模量梁理论。Sino等[8]提出了考虑剪切效应、铺层顺序和纤维方向简化的均质梁理论，分析了系统的临界转速和不稳定阈值。 任勇生等[9]基于变分渐进法(VAM)的复合材料薄壁梁理论引入横向剪切变形，采用Hamiton原理推导出旋转坐标系下轴的自由振动控制方程，研究了复合材料传动轴的动力学特性。

目前，国内外基于有限元方法复合材料轴的研究主要包括：Rangaswamy等[10]采用遗传算法从复合材料铺层数、厚度及铺层顺序等方面对汽车复合材料传动轴进行了优化设计，并利用ANSYS软件进行了静力分析和屈曲分析；Mutasher等[11-12]基于实验和ANSYS有限元软件对混合铝/复合材料驱动轴进行了分析，研究了不同铺层角、铺层数和铺层顺序时轴的承扭性能，并对两种结果进行了对比；Alwan等[13]利用ANSYS 对复合材料薄壁轴和实心轴进行了建模和动态分析，并将分析结果和实验结果进行比较；Khoshravan等[14]基于经典层合板理论对复合材料驱动轴进行了设计并利用ANSYS对其进行了模态分析；徐永健[15]基于ANSYS对复合材料转子系统进行了研究，但是他把转盘作为质量单元来进行建模。由上述研究可以发现，利用ANSYS软件的复合材料轴的有限元研究大多集中在静力分析方面，有关复合材料轴的动力学分析方面的研究报道十分有限，而且所涉及到的研究内容也缺乏系统性和完整性。事实上，有限元法在处理转子动力学问题时，可以很好地兼顾模型的完整性和计算的效率。本研究针对包括轴承、转盘在内的复合材料薄壁轴转子系统，利用有限元软件ANSYS建立了三维实体模型并进行动力学分析，探讨复合材料轴的铺层角度、铺层顺序、长径比、轴承支撑刚度、转盘安装位置对系统固有频率和临界转速的影响，随后分析了转盘质量、转盘安装位置、轴承刚度和轴承阻尼对转子系统不平衡响应的影响。本文建立的有限元模型可以为复合材料薄壁轴转子系统的动力学研究与设计，提供一种可供选择的分析方法。

1 转子动力学分析理论基础

根据弹性力学有限单元理论，通用的动力学运动方程可写为

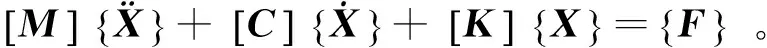
(1)

在转子动力学中，方程式(1)要增加陀螺效应和旋转阻尼[16]，复合材料薄壁轴的动力学方程可表示为

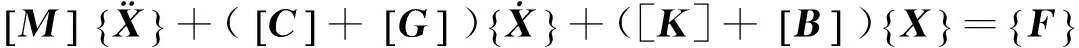
(2)

其中，[G]为陀螺矩阵，取决于转速并对转子动力学计算做主要贡献；[B]为旋转阻尼矩阵，取决于转速且明显地修改结构刚度，并能够使结构产生不平稳运动。

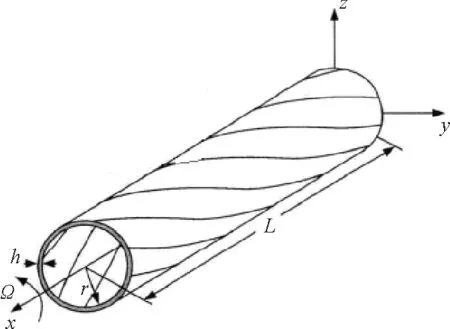
图1 圆截面复合材料薄壁轴

Fig.1 Composite thin-walled shaft of a circular cross-section

2 复合材料薄壁轴转子模型的建立

2.1 复合材料薄壁轴模型的建立

图1为长度为L、厚度为h、截面半径为r的绕其轴线以定常角速度旋转的封闭截面纤维复合材料薄壁轴。

轴的几何尺寸和材料参数分别选取：

长度L=2.47 m，截面半径r=0.063 5 m，厚度h=1.321×10-3m，铺层为等厚度10层，从内到外铺层顺序为[90°,45°,-45°,[0°]6 ,90°]；复合材料为硼/环氧复合材料，性能参数见表1。

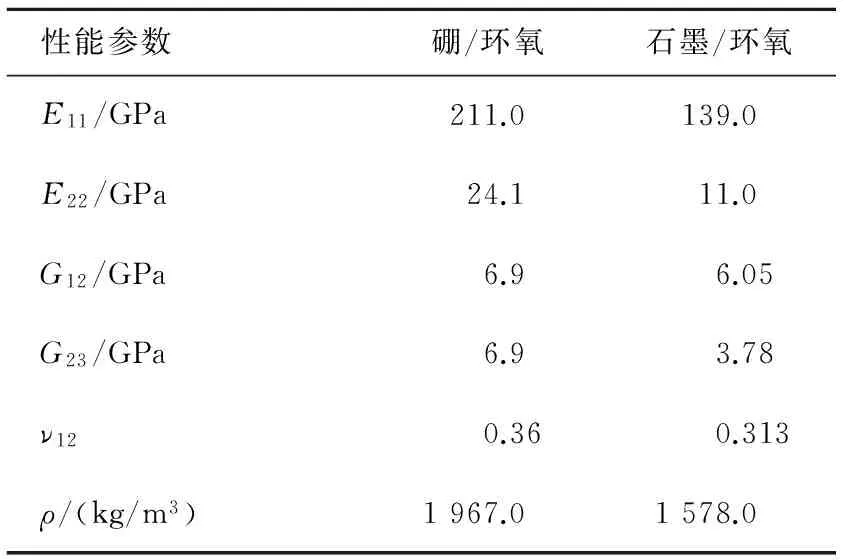
表1 复合材料性能参数

图2 复合材料薄壁轴有限元模型

Fig.2 The ANSYS model of composite thin-walled shaft

由于是薄壁轴，在ANSYS中选择SHELL281单元对复合材料轴进行建模，然后进行网格划分，当划分单元个数为2 910时，模型具有较好的收敛性。图2为复合材料薄壁轴的有限元模型。

考虑简支边界条件，在轴的两个端面上施加x、y、z三个方向的位移约束，选取模态分析类型，进行求解，获取固有频率，求得临界转速。

表2给出了不同研究者采用不同的理论得到的复合材料薄壁轴临界转速，可以看出，采用本文建立的有限元模型所获得的薄壁轴临界转速，在工程精度范围内与已有文献值符合得很好。

表2 复合材料薄壁轴的临界转速

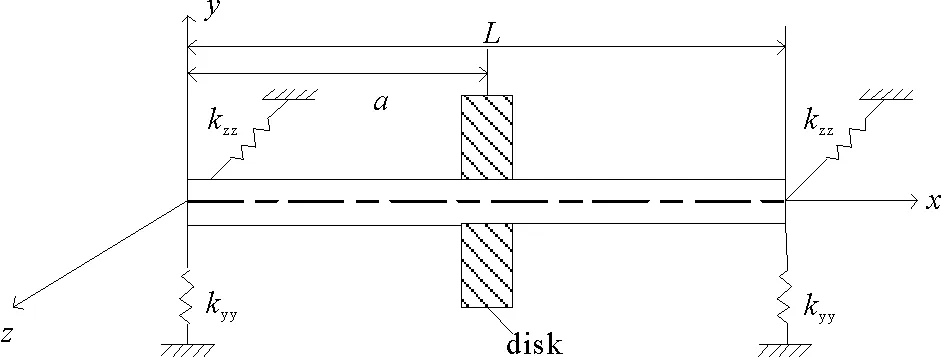
图3 单盘复合材料转子系统

Fig.3 Single-disk composite rotor system

2.2 复合材料轴转子系统模型的建立

在ANSYS中采用相同的复合材料薄壁轴模型，进一步分析包括轴承、转盘在内的复合材料薄壁轴转子系统。系统结构模型如图3所示，单个转盘距传动轴端面的距离为a，轴的两端用轴承支撑。转子系统的尺寸和参数如表3所示。

根据表3给出的尺寸和参数，复合材料轴选用壳单元SHELL281，使用石墨/环氧复合材料其性能参数见表1，铺层为等厚度8层,转盘选用三维实体单元SOLID92，对模型中的支撑轴承考虑用二维轴承单元COMBIN14模拟，建立复合材料薄壁轴转子系统的三维实体有限元模型如图4所示。

表3 复合材料转子系统的尺寸和性能参数

Tab.3 The dimensions and properties of the composite rotor system

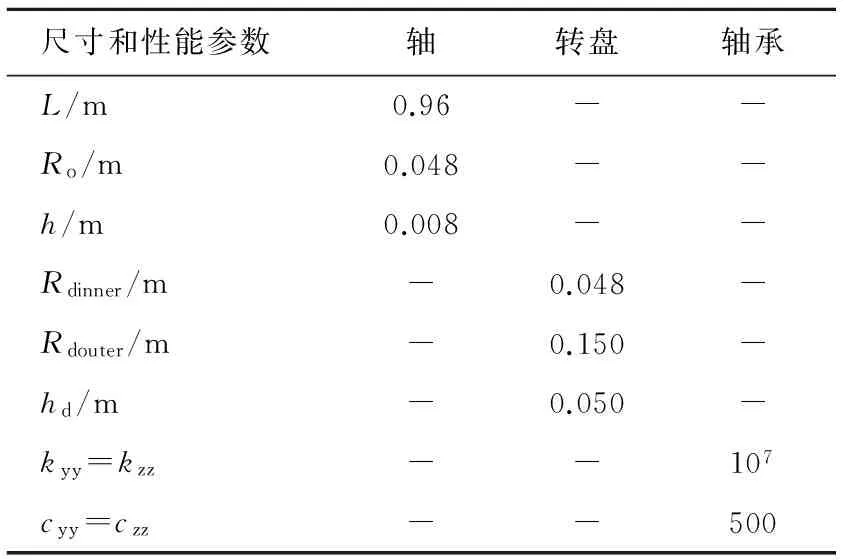
尺寸和性能参数轴转盘轴承L/m0.96--Ro/m0.048--h/m0.008--Rdinner/m-0.048-Rdouter/m-0.150-hd/m-0.050-kyy=kzz--107cyy=czz--500

图4 单盘复合材料转子系统有限元模型

Fig.4 The ANSYS model of single-disk composite rotor system

3 复合材料轴转子系统的有限元计算分析

采用参数化设计语言APDL及命令流，编写复合材料薄壁轴转子系统的参数化设计程序，对转子系统的固有频率、临界转速和振型进行分析。

3.1 模型的收敛性

为验证采用有限元分析方法计算复合材料轴转子系统固有频率的收敛性，假设复合材料薄壁轴的截面铺层方式为[45°]8，取不同的单元数N计算图4系统的前三阶固有频率，结果如表4所示。

表4 单元数对固有频率的影响

Tab.4 Effect of node number N on natural frequencies

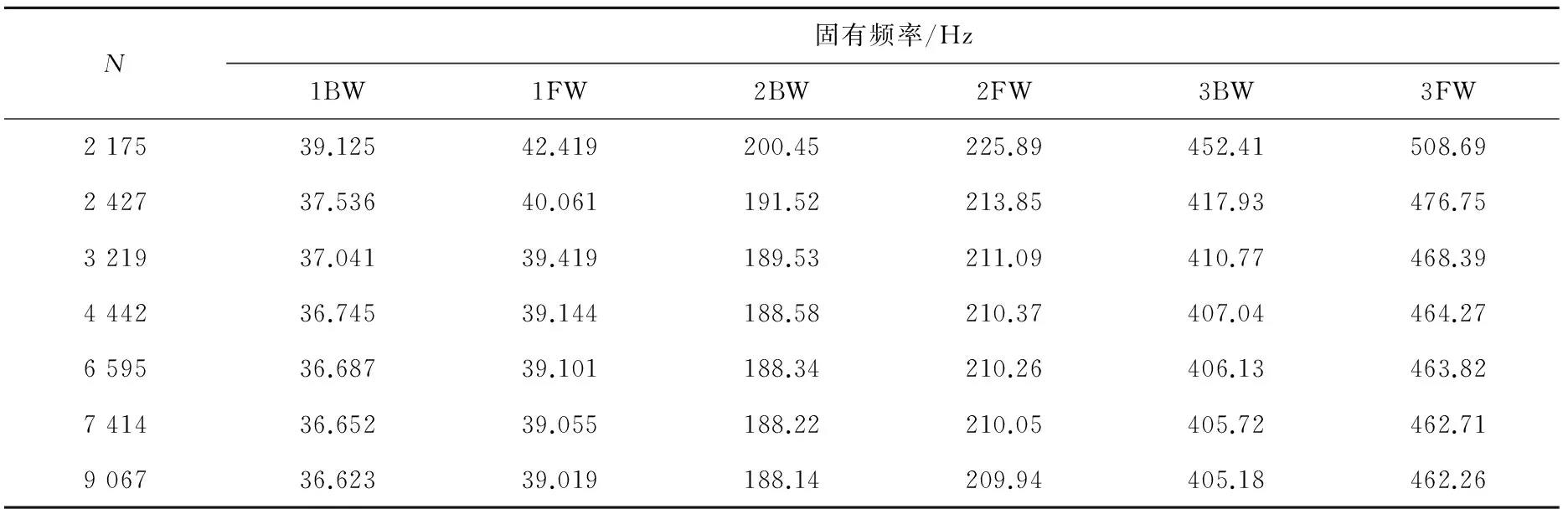
N固有频率/Hz1BW1FW2BW2FW3BW3FW217539.12542.419200.45225.89452.41508.69242737.53640.061191.52213.85417.93476.75321937.04139.419189.53211.09410.77468.39444236.74539.144188.58210.37407.04464.27659536.68739.101188.34210.26406.13463.82741436.65239.055188.22210.05405.72462.71906736.62339.019188.14209.94405.18462.26

“FW”表示正进动，“BW”表示反进动。从表中可以看出，当单元数为9 067时，该模型具有很好的收敛性。

3.2 转子系统的振型分析

图5表示轴截面铺层方式为[45°]8时系统的前三阶模态振型图。从图中可以看出，第一阶弯曲模态在系统的中间部分产生最大位移，在转子旋转且工作转速达到临界转速时产生共振现象，中间比较容易受损。第二阶、第三阶弯曲模态产生最大位移的部位向系统的两端移动，对于第三阶模态，系统的中间部分基本没有位移，当转子旋转达到相应转速时，同样会发生共振现象，转子两端比较容易受损。

图5 单盘复合材料转子系统前三阶模态振型

Fig.5 The first three order model shapes of a composite rotor system

3.3 铺层角度对转子系统固有频率和临界转速的影响

图6～9分别表示转盘位于传动轴的中央位置(a=L/2)时不同铺层角下转子系统的 Campbell 图。图中给出了前3阶涡动频率随转速的变化曲线。图中涡动频率曲线与直线ω=Ω的交点为转子系统的临界转速。可以看出，铺层角度为0°、30°、60°、90°时对应的临界转速分别为3 044.874、2 382.568、1 944.690和1 881.376 rpm。随着铺层角度的增加，系统的固有频率和临界转速逐渐降低。

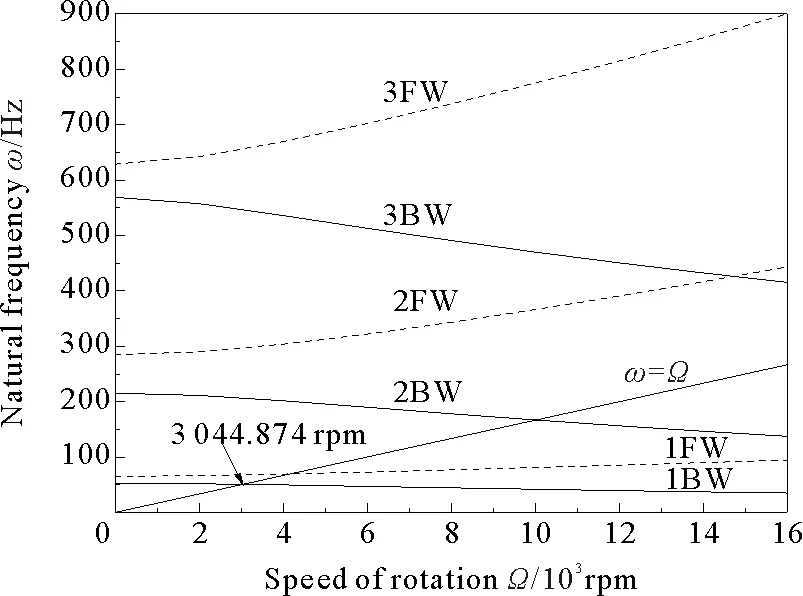
图6 复合材料转子系统的Campbell图([0°]8)

Fig.6 Campbell diagram of a composite rotor system([0°]8)

图7 复合材料转子系统的Campbell图([30°]8)

Fig.7 Campbell diagram of a composite rotor syste ([30°]8)

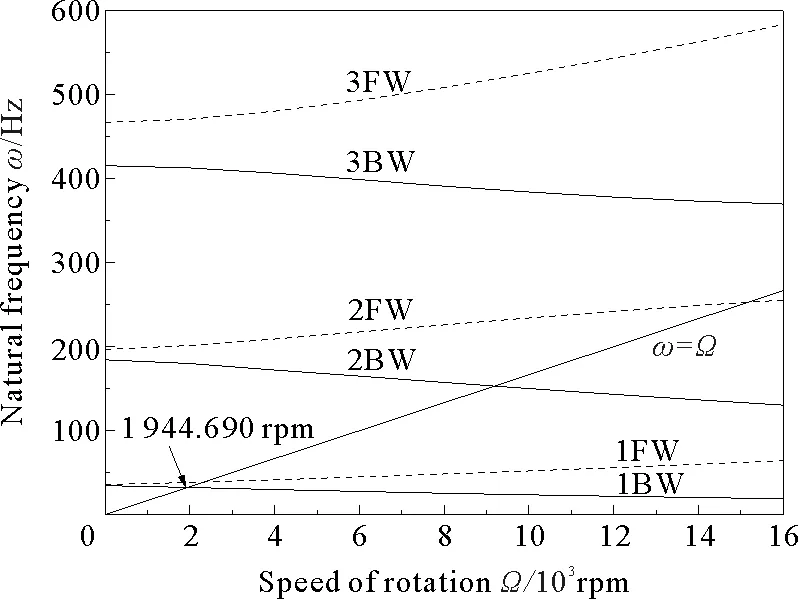
图8 复合材料转子系统的Campbell图([60°]8)

Fig.8 Campbell diagram of a composite rotor system([60°]8)

图9 复合材料转子系统的Campbell图([90°]8)

Fig.9 Campbell diagram of a composite rotor system([90°]8)

3.4 铺层顺序对转子系统固有频率和临界转速的影响

图10、图11分别表示铺层顺序为[90 45 02]s和[0290 45]s时转子系统的 Campbell 图。可以发现，两种情况都包含4层0°纤维铺层、2层90°纤维铺层和2层45°纤维铺层，仅改变铺层顺序，便获得了不同的固有频率和临界转速。由此可以看出，铺层顺序对复合材料轴转子系统有着非常重要的影响。

图10 复合材料转子系统的Campbell图([90 45 02]s)

Fig.10 Campbell diagram of a composite rotor system ([90 45 02]s)

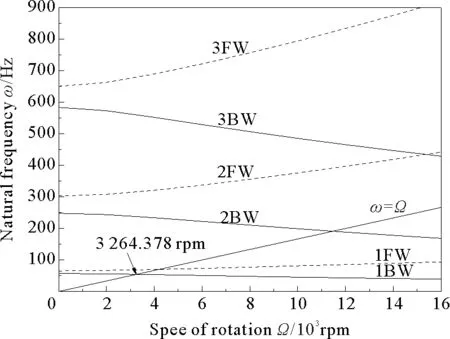
图11 复合材料转子系统的Campbell图([02 90 45]s)

Fig.11 Campbell diagram of a composite rotor system([0290 45]s)

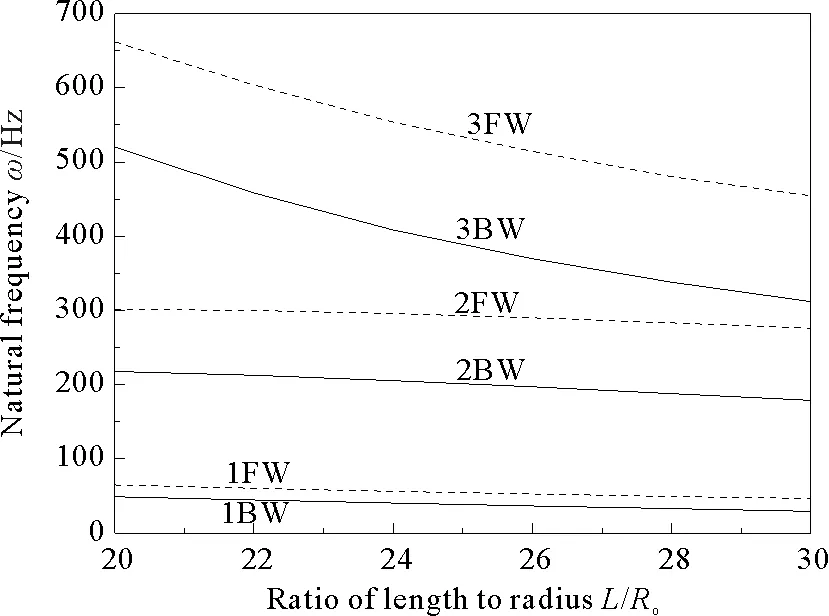
图12 复合材料转子系统的固有频率随长径比的变化曲线

Fig.12 Natural frequency of a composite rotor system versus ratio of length to radius

3.5 轴长径比对转子系统固有频率的影响

设定复合材料轴的铺层方式为[±30°]4s，轴承支撑刚度为1×107N/m，转子转速为4 000 r/min时，分析轴的长径比对转子系统固有频率的影响。

图12表示复合材料转子系统的前三阶旋转固有频率随长径比的变化曲线。从图中可以看出，转子系统的固有频率随着长径比的增加而降低。

3.6 轴承刚度对转子系统固有频率的影响

设定复合材料轴的铺层方式为[±30°]4s，转子转速为0时，分析轴承不同刚度对转子系统固有频率的影响。结果如表5所示，从表中可以看出，随着支承刚度的增加，系统的固有频率得到提高。当支承刚度在1×105～1×108N/m范围内变化时，固有频率提高的非常快，当支承刚度增加到1×109N/m时，转子系统的固有频率随轴承刚度的增大变化很小。

3.7 转盘偏置对转子系统固有频率和临界转速的影响

设定复合材料轴的铺层方式为[±30°]4s，轴承支撑刚度为1×107N/m，选取转盘距复合材料轴左端面的距离分别为转轴长度的1/2、1/4、1/6、1/8，作出这四种偏置情况的转子系统的坎贝尔图。

从图13～16可以看出，转盘偏置L/2、L/4、L/6和L/8时，对应的临界转速分别为3 008.439、3 117.572、3 290.533和3 497.314 rpm。由此可见，转盘偏置程度越大，转子系统一阶临界转速越高。通过观察可发现，转子系统的二阶、三阶固有频率则随着转盘偏置程度的增大而降低。

表5 轴承不同刚度对复合材料转子固有频率的影响

Tab.5 The influence on natural frequency of composite rotor for different bearing stiffness

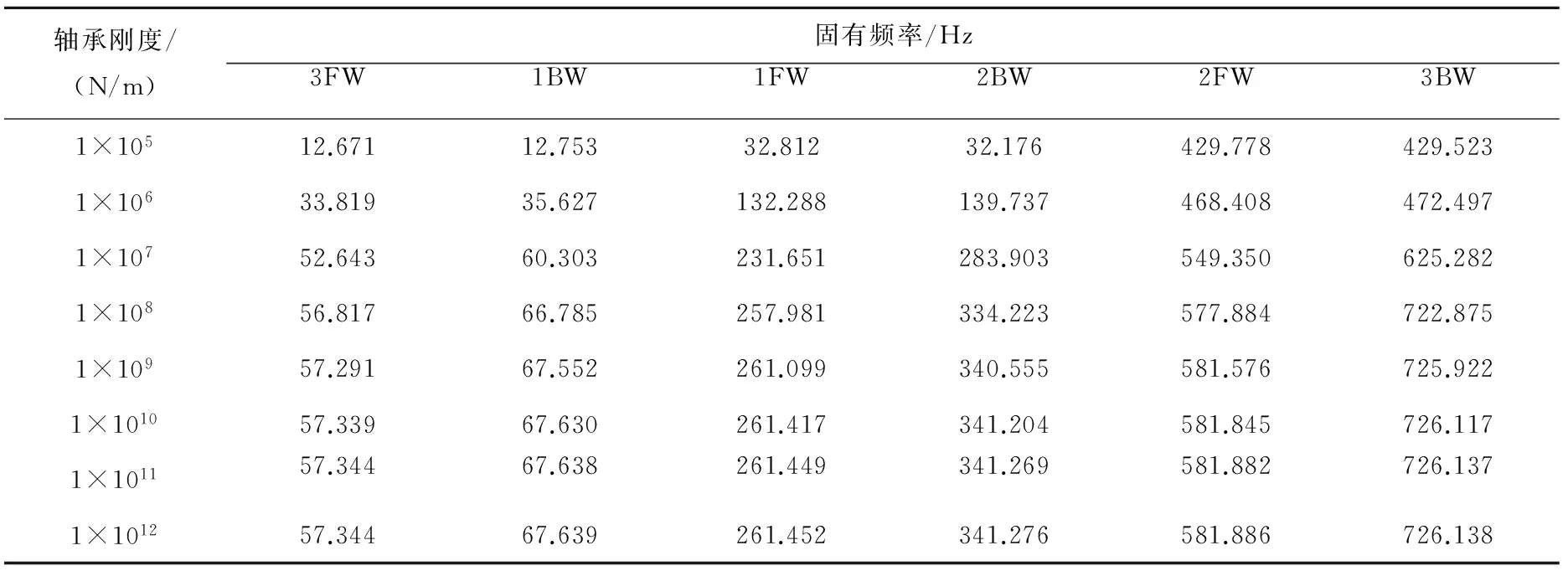
轴承刚度/(N/m)固有频率/Hz1BW1FW2BW2FW3BW3FW1×10512.67112.75332.81232.176429.778429.5231×10633.81935.627132.288139.737468.408472.4971×10752.64360.303231.651283.903549.350625.2821×10856.81766.785257.981334.223577.884722.8751×10957.29167.552261.099340.555581.576725.9221×101057.33967.630261.417341.204581.845726.1171×101157.34467.638261.449341.269581.882726.1371×101257.34467.639261.452341.276581.886726.138

图13 转盘偏置L/2时转子系统的Campbell图

Fig.13 Campbell diagram of the offset rotor system(a=L/2)

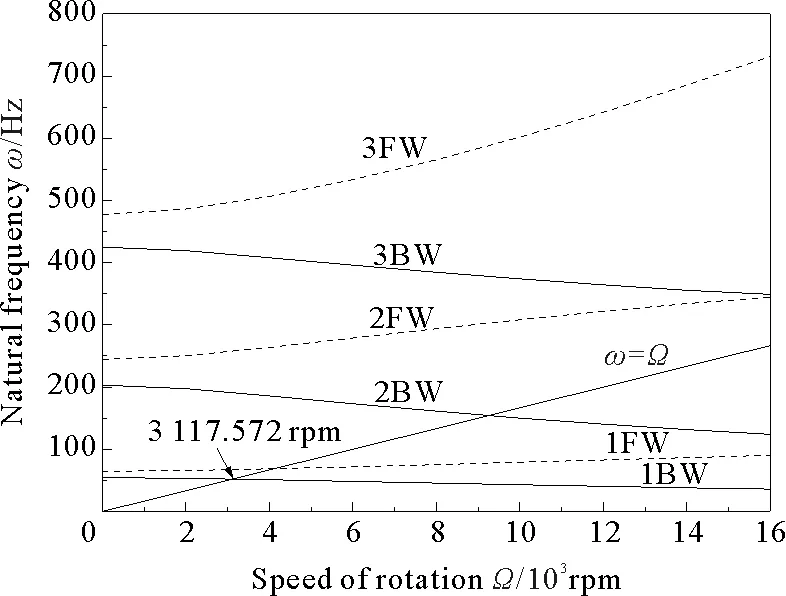
图14 转盘偏置L/4时转子系统的Campbell图

Fig.14 Campbell diagram of the offset rotor system (a=L/4)

图15 转盘偏置L/6时转子系统的Campbell图

Fig.15 Campbell diagram of the offset rotor system(a=L/6)

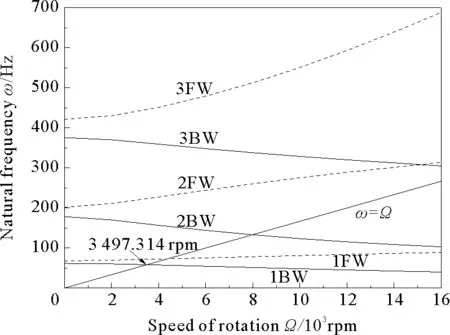
图16 转盘偏置L/8时转子系统的Campbell图

Fig.16 Campbell diagram of the offset rotor system(a=L/8)

3.8 不平衡响应分析

设定复合材料轴的铺层方式为[±30°]4s，转子转速为4 000 r/min，考察转子系统的径向位移频率响应，设置分析的频率范围为0～200 Hz，共100个子步。提取转盘外缘节点随频率变化的径向位移值，绘制转盘中心Y方向的频率响应曲线。

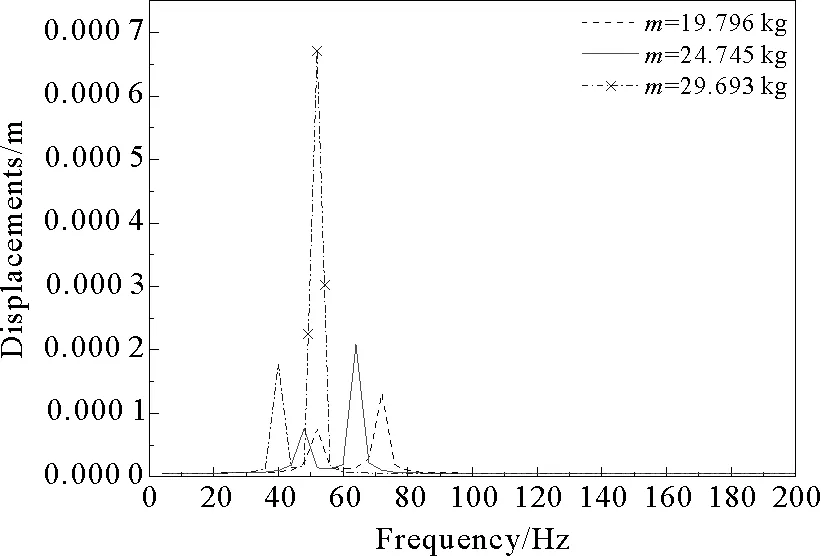
图17 转盘质量对频率响应曲线的影响

Fig.17 Effect of the disk mass on the frequency response curve

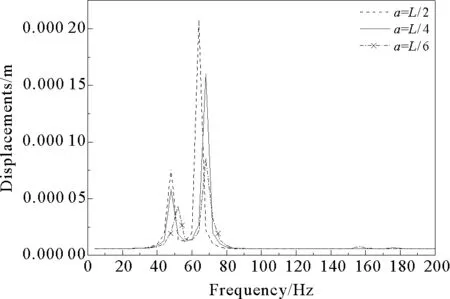
图18 转盘安装位置对频率响应曲线的影响

Fig.18 Effect of the disc installation position on the frequency response curve

图17中，当转盘质量分别为19.796、24.745和29.693 kg时， 转盘中心Y方向产生的振动幅值为1.315×10-4、2.078×10-4和6.726×10-4m。由此可以看出，随着转盘质量的增加系统的不平衡响应幅值相应变大。

图18中，当转盘安装位置距离轴端面分别为L/2、L/4和L/6时， 转盘中心Y方向产生的振动幅值为2.078×10-4、1.603×10-4和8.531×10-5m。由此可以看出，随着转盘偏置程度的增加系统的不平衡响应幅值相应变小。

图19中，当轴承刚度分别为0.5×107、1×107和2×107N/m时， 转盘中心Y方向产生的振动幅值为2.427×10-4、2.078×10-4和9.375×10-5m。由此可以看出，随着轴承刚度的增加系统的不平衡响应幅值相应变小。

图19 轴承刚度对频率响应曲线的影响

Fig.19 Effect of the bearing stiffness on the frequency response curve

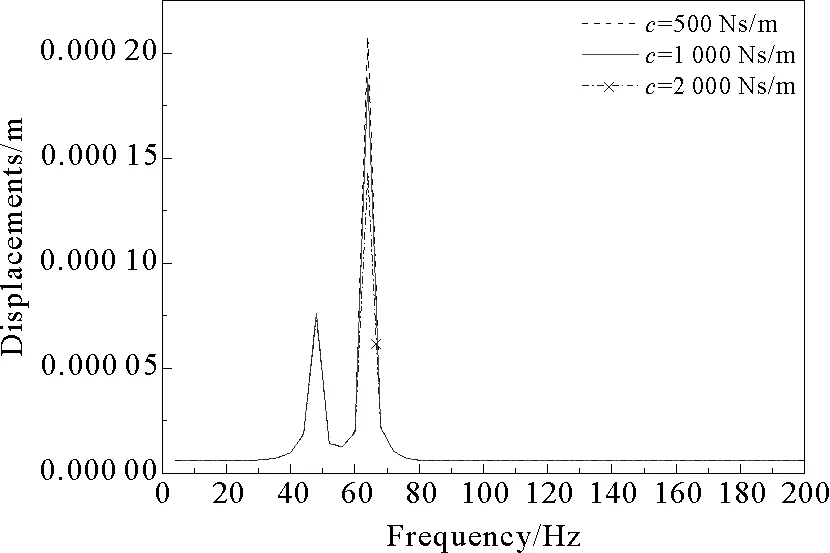
图20 轴承阻尼对频率响应曲线的影响

Fig.20 Effect of the bearing damping on the frequency response curve

图20中，当轴承阻尼分别为500、1 000和2 000 Ns/m时， 转盘中心Y方向产生的振动幅值为2.078×10-4、1.879×10-4和1.431×10-4m。由此可以看出，随着轴承阻尼的增加系统的不平衡响应幅值相应变小。

4 结论

本文在ANSYS中建立了复合材料薄壁轴的有限元模型，采用SHELL281单元进行了网格划分，得出了转子系统的临界转速，并与文献作比较，验证了模型的正确性。然后建立了包含转盘-轴承在内的复合材料薄壁轴转子系统的有限元模型，研究了转子系统的动力学特性。有限元计算分析结果表明：

1) 当复合材料轴的铺层角度或长径比增加时，转子系统的固有频率和临界转速随之降低；“BW”表示反向涡动频率曲线，固有频率随转速的增加而降低，“FW”表示正向涡动频率曲线，固有频率随转速的增加而增加；当复合材料轴的铺层角度和层数相同而铺层顺序不同时，转子系统的固有频率和临界转速变化很大，因此可通过改变铺层顺序对转子系统进行优化设计；

2) 轴承刚度越大，转子的固有频率越高，当轴承刚度大到一定的数值后，转子的固有频率随轴承刚度的变化很小，稳定在一个固定数值附近；

3) 由于陀螺效应的影响，转盘偏置程度越大，低阶固有频率越高，而高阶固有频率则相应降低；

4) 转子系统在临界转速附近发生共振，并且振动幅值随着转盘质量的增加而增大，随着转盘偏置程度、轴承刚度、轴承阻尼的增加而减小。

本文建立的有限元模型可以为复合材料薄壁轴转子系统的动力学研究与设计，提供一种可供选择的分析方法。

[1]ZHAO S X,XU H,MENG G,et al.Stability and response analysis of symmetrical single-disk flexible rotor-bearing system[J].Tribology International,2005,38:749-756.

[2]ZINBERG H,SYMMONDS M F.The development of an advanced composite tail rotor driveshaft[C]∥Presented at the annual national forum of the American helicopter society.June,Washington,D C,1970:1-14.

[3]BERT C W,Kim C K.Whirling of composite material drive shafts including bending-twisting coupling and transverse shear deformation[J].Journal of Vibration and Acoustics,1995,117(1):7-21.

[4]SINGH S P,GUPTA K.Composite shaft rotor dynamic analysis using a layer wise theory[J].Journal of Sound and Vibration,1996,191(5):739-756.

[5]EL MAHDY T H,GADELRAB R M.Free vibration of unidirectional fiber reinforcement composite rotor[J].Journal of Sound and Vibration,2000,230(1):195-202.

[6]CHANG M Y,CHEN J K,CHANG C Y.A simple spinning laminated composite shaft model[J].International Journal of Solids and Structures,2004,41:637-662.

[7]GUBRAN H B H,GUPTA K.The effect of stacking sequence and coupling mechanisms on the natural frequencies of composite shafts[J].Journal of Sound and Vibration,2005,282:231-248.

[8]SINO R,BARANGER T N,CHATELET E,et al.Dynamic analysis of a rotating composite shaft[J].Composites Science and Technology,2008,68:337-345.

[9]任勇生,代其义,张兴琦.旋转复合材料薄壁轴的自由振动与稳定性[J].振动工程学报,2015,28(1):59-66. REN Yongsheng,DAI Qiyi,ZHANG Xingqi.Free vibration and stability of a rotating thin-walled composite shaft[J].Journal of Vibration and Engineering,2015,28(1):59-66.

[10]RANGASWAMY T,VIJAYARANGAN S,CHANDRASHEKAR R A,et al.Optimal design and analysis of automotive composite drive shaft[C]∥Proceeding of International Symposium of Reaearch Students on Materials Science and Engineering.Madras,India,Dec.2004.

[11]MUTASHER S A,SAHARI B B,HAMOUDA A M S,et al.Static and dynamic characteristics of a hybrid aluminium/composite drive shaft[J].Journal of Materials:Design and Applications,2007,221:63-75.

[12]MUTASHER S A.Prediction of the torsional strength of the hybrid aluminum/composite drive shaft[J].Materials and Design,2009,30:215-220.

[13]ALWAN V,GUPTA A,SEKHAR A S,et al.Dynamic analysis of shafts of composite materials[J].Journal of Reinforced Plastics and Composites,2010,29(22):3364-3379.

[14]KHOSHRAVAN M R,PAYKAN A.Design of a composite drive shaft and its coupling for automotive application[J].Journal of Applied Research and Technology,2012,10:826-834.

[15]徐永健.基于ANSYS的复合材料转子系统的振动分析[D].青岛:山东科技大学,2014.

[16]闻邦春,顾家柳,夏松波,等.高等转子动力学-理论技术与应用[M].北京:机械工业出版社,2000.

(责任编辑：李 磊)

Finite Element Simulation of Dynamic Characteristics of Composite Thin-walled Shaft Rotor System

ZHONG Weiyan1,REN Yongsheng1,GAO Feng1,LIU Lei2,LIU Jie3

(1.College of Mechanical and Electronic Engineering,Shandong University of Science and Technology,Qingdao,Shandong 266590,China;2.Chengfa Investment Group Co.Ltd,Qingdao,Shandong 266555,China;3.Department of Electrical Engineering & Information Technology,Shandong University of Science and Technology,Jinan,Shandong 250031,China)

A finite element model was first established for a composite thin-walled shaft system by using the finite element software ANSYS. Through modal analysis,the natural frequency and the critical speeds were obtained and by comparing the results with those in other related literature,the validity of this model was proved. Then a finite element model for a composite thin-walled shaft rotor system which includes bearing and rigid disk was established to study the dynamic characteristics of the rotor system. The effects of the composite fiber orientation,fiber stacking sequence,ratios of length over radius,bearing stiffness and disc installation position in the shaft on the natural frequency and the critical speeds were discussed. Afterwards,the effects of disk mass,disc installation position,bearing stiffness and bearing damping on the imbalance response of the rotor system were analyzed. This method provides an alternative analytical method for the study and design of the composite thin-walled shaft-rotor system.

composite material; thin-walled shaft; natural frequency; critical speed; unbalance response

2016-03-02

国家自然科学基金项目(11272190)

仲惟燕(1978—)，女，河北南宫人，讲师，博士研究生，主要从事机械系统动力学、非线性振动与控制研究. E-mail：weiyanzh@163.com

TB33；TH133

A

1672-3767(2016)05-0087-09