基于PCA-BP神经网络的非常规储层岩性识别研究
胡嘉良,高玉超,余继峰,卢 磊,张鸿君,杨子群
(1.山东科技大学 地球科学与工程学院,山东 青岛 266590;2.兖矿东华建设有限公司 地矿建设分公司,山东 邹城 273500)
基于PCA-BP神经网络的非常规储层岩性识别研究
胡嘉良1,高玉超2,余继峰1,卢 磊1,张鸿君1,杨子群1
(1.山东科技大学 地球科学与工程学院,山东 青岛 266590;2.兖矿东华建设有限公司 地矿建设分公司,山东 邹城 273500)
岩性识别一直是储层测井解释的关键问题和难点之一。针对常规测井岩性识别准确率不高的状况,在分析测井资料的基础上,以Matlab为平台研究了基于主成分分析的PCA-BP神经网络,并以济阳坳陷非常规储层实际测井资料为样本,通过设计算法步骤进行了实验仿真。由仿真结果得出非常规储层岩性识别率为95.8%,高于BP神经网络,PCA-BP神经网络有效提高了识别率和运行速度。经过对济阳坳陷钻井的岩性识别表明,该岩性识别方法可行并具有实用价值。
非常规储层;济阳坳陷;岩性识别;主成分分析;BP神经网络
近年来,随着我国油气供求矛盾突出以及常规油气资源不断减少,非常规油气的勘探与开发逐渐受到重视,而非常规油气储层具有储层结构复杂、渗透性异常、埋藏较深、勘探开发难度较大的特点,这对油气勘探开发技术提出了更高的要求[1]。精确高效的测井资料岩性识别技术能为油气资源勘探开发提供有力保障。随着油气勘探技术的不断发展,神经网络已经成为测井岩性识别的重要手段之一,一些经过优化的神经网络模型在测井岩性识别中取得了较好效果。周成当[2]提出了模糊神经网络结合贝叶斯统计模式的岩性识别模型,并验证了该方法的可行性;范训礼等[3]应用神经网络对塔里木油田某取芯井的测井资料进行了泥岩、砂岩和灰岩的岩性识别,证实了神经网络在岩性识别中的有效性;金明霞等[4]利用快速BP算法训练了神经网络,并用训练后的神经网络对某地区的测井资料进行岩性识别,取得了相当好的效果;罗德江等[5]考虑到BP神经网络的不足,结合小波变换,将小波神经网络应用到致密砂岩储层参数的预测中,较为准确地预测储层孔隙度,为储层参数预测提供了新思路;怀海宁等[6]利用神经网络模型对镇原区块储层的物性参数进行了预测,又一次证实了BP神经网络在测井参数预测应用中的优势和潜力;张国英等[7]将主成分分析与神经网络相结合,提出了基于主成分分析的BP网络储层岩性识别模型,并证实了该模型的优越性能。
主成分分析(Principal Component Analysis, PCA)是一种较为常用的多变量统计方法,将多个变量转换为少数的几个主成分,将原始数据简化,起到了降维的效果。BP神经网络已较为广泛地应用于目标分类与预测识别。针对BP神经网络的缺陷与不足,防止BP神经网络由于前端输入太多的样本特征量,造成训练速度与效率降低,甚至不收敛的情况,结合主成分分析对输入的样本进行降维[8]。基于主成分分析的BP神经网络模型,结合二者的优点,使网络性能更高。该方法降低了神经网络的复杂度,减少了运行时间,提高了计算精度[9-12]。
1 理论与方法简介
1.1 主成分分析原理

主成分分析方法的计算步骤[14-15]:
2)计算变量之间的相关系数矩阵R,R=XX′(N-1)-1;
3)计算R的特征值λj及其对应的特征向量μj(j=1,2,…,p);
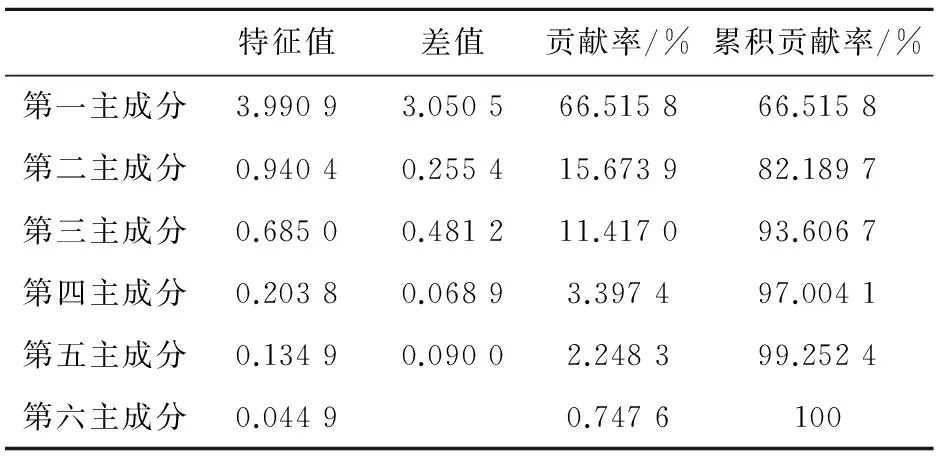
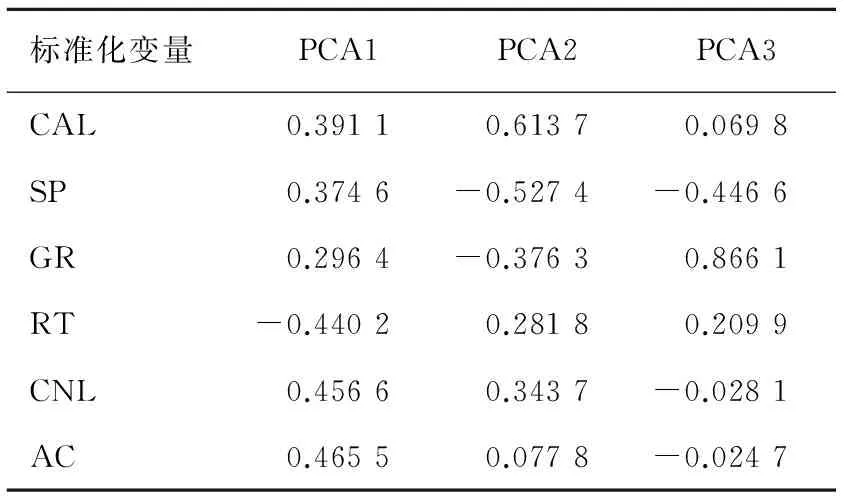
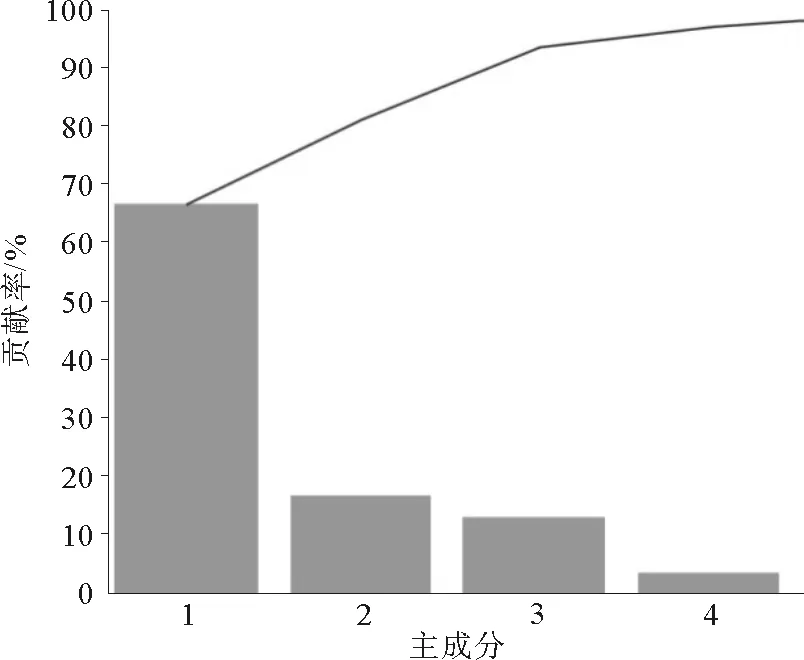
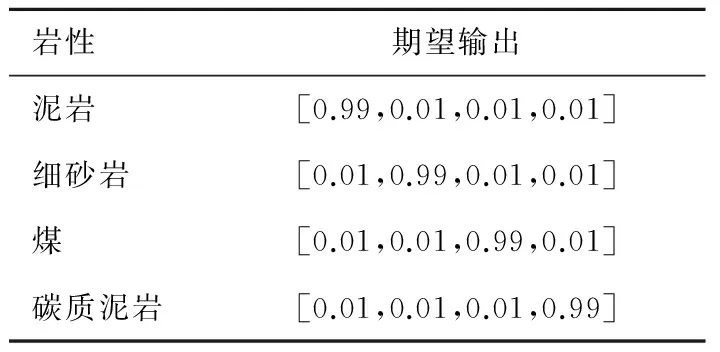
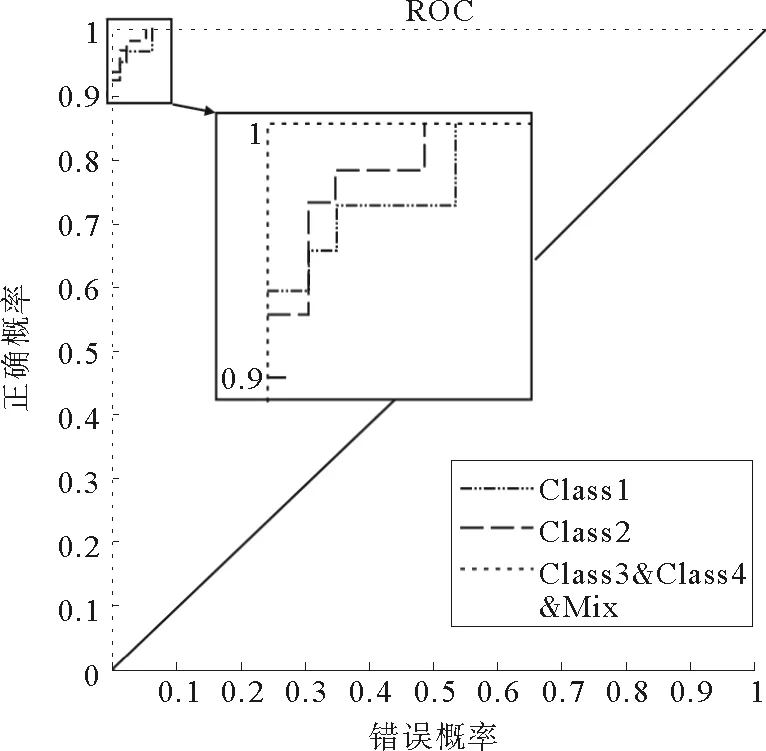
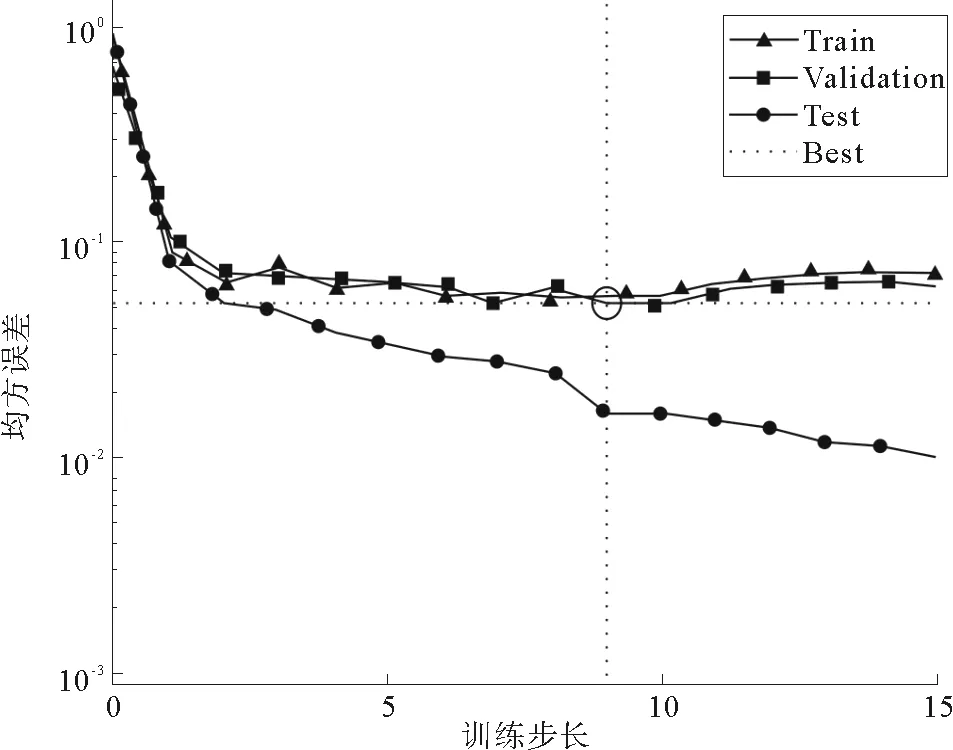
4)计算主成分累计贡献率,确定m(m 通常以大于85%的累计贡献率来确定m的取值; 5)取前m个主成分并计算各个样品在主成分上的得分,第i个样品的第j个主成分为:Fij=μijx1i+μ2jx2i+…+μpjxpi,(i=1,2,…,n;j=1,2,…,m); 1.2 BP神经网络原理 BP神经网络是一种多层前馈网络,它既有信号的前向传递又有误差的反向传递,网络模型的拓扑结构分为输入层、隐层和输出层。在信号前向传递过程中,输入信号从输入层经过隐层传输到输出层,进行逐层处理,每一层的神经元信号只能传递到下一层神经元;如果输出层的输出结果未达到事先给定的期望输出,则误差转入反向传播,根据误差的大小调整神经网络的权值和阈值,使网络能够收敛到较小的均方误差,从而使预测输出不断逼近期望输出。这一神经网络训练的过程使得网络学习并储存了输入和输出变量之间的映射关系。 BP网络用于测井岩性识别的基本原理是:应用参数井的测井信息与相应岩层参数值对网络进行学习训练,使其获得判别井径、自然伽玛、自然电位、声波时差等参数经验,以及对预测参数的倾向性认识。当对未知岩性的井段测井参数进行岩性识别时,网络将利用已形成的映射关系,再现专家经验,实现定性与定量的有效结合,保证岩性识别、分层的结果的客观与准确。 1.3 PCA-BP网络结构及识别步骤 PCA-BP网络由两部分构成:一是主成分分析;二是BP神经网络。结构图如图1所示。 图1 PCA-BP网络结构 Fig.1 PCA-BP network structure 识别步骤: 1) 训练样本数据主成分分析。合理选择训练样本测井参数,并进行标准化。求取标准化后样本数据的相关系数矩阵,计算相关矩阵的特征值和特征向量。选取累积贡献率大于85%的前m个特征值及其对应的特征向量,并计算出前m个主成分的得分。 2) 网络训练,建立识别模型。以第一步得到的前m个主成分的得分为学习样本,输入BP神经网络进行训练。 3) 网络测试。按照第一步和第二步的方法,取测试样本测井参数数据,进行主成分分析并将测试样本测井参数的主成分得分输入已经建立好的PCA-BP网络模型中,网络模型按照已有学习经验对测试样本进行岩性识别。 2.1 样本参数PCA处理 考虑到建立的神经网络模型应具有合理性与泛化能力,样本的选择尤为重要。应充分考虑岩性类别与测井物性参数之间的内在联系和特定的区域地质背景,选取标准的岩性样本。以济阳坳陷渤93钻测井数据为研究对象,选择能够敏感映射该区非常规储层岩性的测井参数值,即井径(CAL)、自然电位(SP)、声波时差(AC)、补偿中子(CNL)、地层真电阻率(RT)和自然伽玛(GR),用于分析识别泥岩、碳质泥岩、煤层及细砂岩的岩性类型。 图2 测井参数的皮尔逊相关系数 Fig.2 Pearson correlation coefficient of log parameters 一般不同测井参数间的数值大小相差较大,为了消除测井数据在量纲与数量级上存在的差异,首先将测井数据进行归一化处理。处理后的测井数据没有量纲并且其数值在[0,1]范围内变化。采用最常用的极值归一化方法,公式为:Zij=(Xij-Xij min)(Xij max-Xij min)-1,其中:i=1,2,…,n;j=1,2,…,p;Zij为归一化后的数据;Xij为原始数据;Xij max、Xij min分别为某曲线的最大值、最小值。 网络训练样本数据越多,模型的泛化能力越好。选取160个样本数据,将样本数据的70%作为训练数据,15%作为验证数据,15%作为测试数据。将归一化后的样本测井数据,先进行相关性检测再进行主成分分析。 由测井参数的皮尔逊相关系数(图2)可见,除地层真电阻率(RT)以外的测井参数间呈正相关或弱的正相关,地层真电阻率(RT)与其余测井参数呈强的负相关。所以需要对测井参数进行主成分分析以降维减小数据的冗余度。 表1、2、3及图3、4为测井数据主成分分析后的部分结果。由表1及图3可见,前三个主成分的累积贡献率已达到93.6%,因此前3个主成分基本代表原有信息,后几个主成分的贡献率很小,可以将其忽略。由表2可见,PCA1主要反映测井参数CNL、AC和RT对测井岩性的综合影响,PCA2反映测井参数GR、SP和CAL对测井岩性的综合影响,PCA3主要反映SP、GR和RT对测井岩性的综合影响。 表1 各主成分的特征值及贡献率 Tab.1 Characteristic values of the principal component and the contribution rate 特征值差值贡献率/%累积贡献率/%第一主成分3.99093.050566.515866.5158第二主成分0.94040.255415.673982.1897第三主成分0.68500.481211.417093.6067第四主成分0.20380.06893.397497.0041第五主成分0.13490.09002.248399.2524第六主成分0.04490.7476100 表2 主成分系数 Tab.2 Coefficient of principal component 标准化变量PCA1PCA2PCA3CAL0.39110.61370.0698SP0.3746-0.5274-0.4466GR0.2964-0.37630.8661RT-0.44020.28180.2099CNL0.45660.3437-0.0281AC0.46550.0778-0.0247 表3 部分原始样本及其主成分得分数据 Tab.3 Part of the original sample data and principal component score data 编号测井原始数据CALSPGRRTCNLAC主成分得分PCA1PCA2PCA3录井岩性126.96650.2598.1219.76917.241222.9970.80351.61820.0910泥岩226.96650.2478.2949.36217.472222.9970.89841.56190.1844泥岩326.96750.2478.7578.86217.748224.4871.09921.42540.4579泥岩426.96750.2478.9328.39317.923221.7791.14541.35130.5517泥岩526.40049.668.05712.39418.42213.9720.32251.73930.2063细砂岩626.29749.678.26212.25517.716217.0750.35981.60590.3285细砂岩726.33349.5158.43611.92817.026220.1970.42241.53070.4426细砂岩826.37349.6248.32511.65116.693222.660.45761.53120.3491细砂岩922.61852.6548.21111.3239.248206.795-0.9492-0.4419-0.0962煤层1022.54652.8088.17111.0239.328207.802-0.9057-0.4788-0.1537煤层1122.44352.9378.36510.7169.196208.844-0.8353-0.6016-0.0582煤层1222.29553.0668.22610.3988.94210.221-0.8503-0.6521-0.1791煤层1322.59152.8616.9315.66811.711207.013-1.40740.3049-0.7634碳质泥岩1422.60552.756.62816.39712.424212.943-1.37430.5145-0.9246碳质泥岩1522.52852.7126.39617.10312.728214.899-1.44550.6289-1.0455碳质泥岩1622.33452.4875.76816.52111.986207.801-1.78250.6671-1.4504碳质泥岩 图3 贡献率直方图 Fig.3 Histogram contribution rate 图4 主成分得分的散点图 Fig.4 Principal component scores scatterplot 2.2 网络训练及性能 构建由3层神经元组成的BP神经网络模型。输入层为训练样本的前3个主成分得分,输出层是测井识别目标值,由4个神经元组成,即4种非常规储层岩性(泥岩、碳质泥岩、煤层和细砂岩)。隐层神经元个数的确定采用网络结构增长型方法,在建立网络时,由于隐层神经元激活函数采用了S型函数,输出层的各个神经元输出只能无限接近1和0,而不能够达到1和0,因此在对各训练样本的期望值进行编码时,设置为0.99和0.01。对网络期望输出编码如表4。 表4 网络输出编码 Tab.4 Network output encoding 岩性期望输出泥岩[0.99,0.01,0.01,0.01]细砂岩[0.01,0.99,0.01,0.01]煤[0.01,0.01,0.99,0.01]碳质泥岩[0.01,0.01,0.01,0.99] 将主成分得分送入BP网络模型进行训练,选取f(x)=(1+e-x)-1为激活函数,初始步长为1,动量因子α=0.6,最大迭代次数为500次,目标误差ε=0.01,学习率为0.01,隐含层节点数为30个。采用Matlab2012b平台,将训练样本输入计算机程序,对网络进行学习训练,网络训练结果如下: 1)ROC曲线 图5 ROC曲线图 Fig.5 ROC plot 图5受试者特征曲线(Receiver Operating Characteristic Curve,简称ROC曲线),横轴为虚报概率即错误的判断率,纵轴为击中概率即正确的判断率;ROC曲线下方面积(Area Under the ROC,简称AUC)在1.0和0.5之间。AUC越接近0.5说明识别准确性越差,AUC越接近于1说明识别准确性越好。图5中显示绘制的曲线都远离斜45°直线,AUC都大于0.9,说明PCA-BP网络模型的识别能力较好。 2)混淆矩阵 采用混淆矩阵(图6)对识别结果加以说明,矩阵的列分别表示某种岩性实际类别,行表示识别结果。矩阵对角线上的数据代表被正确分类的样本个数,非对角线上的数据代表被混分的样本个数;从图看出,泥岩、细砂岩、煤层、碳质泥岩被正确识别的样本个数分别为57、62、16和20。以“1”所代表的“泥岩”为例,第1行中的“57”代表有57个样本被识别为泥岩,“2”代表有2个细砂岩样本被混淆识别为泥岩。即在识别结果中有被正确识别为泥岩的57个样本和被错误识别的2个样本,其识别结果的符合率(被正确识别样本数占该类别识别结果总样本数的比)为96.6%,第1列代表实际有60个泥岩样本,其中3个被误判为细砂岩,其识别结果的正确率(被正确识别样本数占该类别实际样本数的比)为95%。细砂岩的识别结果符合率为95.4%、煤层为100%、碳质泥岩为100%、总学习结果符合率为96.9%。泥岩和细砂岩出现混淆,识别符合率较低,这是因为泥岩与细砂岩岩性特征相近,不利于识别。 3)网络训练收敛图 由Matlab程序仿真得到神经网络训练收敛图(图7),随着训练步数的增加,均方误差越来越小,训练曲线距离目标误差越来越接近,当训练曲线与目标误差曲线相交时,本次训练收敛。PCA-BP神经网络的最佳表现性能在训练步长为9步,均方误差为0.052 097时取得。 4)线性回归分析图 把所有数据(训练数据、验证数据以及测试数据)放到一个数据集中,通过网络输出和期望输出进行线性回归分析,分析结果如图8所示:所有数据的输出相对于期望值都有较好的跟踪,相应的R值都达到0.8以上,网络响应效果较好。 注:1—泥岩,2—细砂岩,3—煤层,4—碳质泥岩 图6 混淆矩阵图 Fig.6 Confusion matrix 图7 网络训练收敛图 Fig.7 Network training convergence map 图8 线性回归结果图 Fig.8 Linear regression results 表5 PCA-BP网络与BP网络识别结果比较 Tab.5 Recognition results compared to BP neural network 网络类型收敛步长识别率/%BP神经网络1583.3PCA-BP神经网络995.8 2.3 网络识别结果对比 测试数据用于验证网络的识别率,由24个测试数据的识别结果发现,PCA-BP神经网络有1个数据识别错误,BP神经网络有4个数据识别错误。 综合对比(表5)发现:PCA-BP神经网络的收敛步长为9,BP神经网络为15,说明PCA-BP神经网络收敛性好,效率更高;PCA-BP神经网络识别率为95.8%,高于BP神经网络的83.3%,说明PCA-BP神经网络识别精度更高。 应用以上建立的PCA-BP神经网络模型,另取济阳坳陷渤93钻井2 850~2 943 m的测井数据为待识别样本,将样本送入已经训练好的PCA-BP网络岩性识别模型中进行识别,识别结果如图9所示。从图9中可以看出,PCA-BP神经网络的识别结果与录井岩性吻合,尤其是2 875~2 883 m泥岩段识别的结果更加精细,在2 884.5~2 886.5 m段识别出了煤夹层。 图9 渤93钻井2 850~2 943 m岩性识别结果 Fig.9 Wells Bo93 2 850-2 943 m lithology identification results 利用主成分分析法对济阳坳陷测井样本参数进行优化,减少了输入维数,消除了各变量之间的自相关性,简化了神经网络结构。以济阳坳陷测井数据为研究对象建立的PCA-BP神经网络模型的收敛步长为9,低于BP网络的15,显示出更好的收敛性,PCA-BP神经网络的运行效率较高;PCA-BP神经网络识别准确率为95.8%,高于BP神经网络的83.3%。在同一口井中,利用取芯段测井参数建立PCA-BP神经网络,可以对未取芯段进行岩性识别。PCA-BP神经网络是一种经济高效的测井资料地质解释方法,可以作为非常规油气资源开发领域中实用的技术手段。 [1]赵靖舟.非常规油气有关概念、分类及资源潜力[J].天然气地球科学,2012,23(3):393-406. ZHAO Jingzhou.Conception,classification and resource potential of unconventional hydrocarbons[J].Natual Gas Geo-science,2012,23(3):393-406. [2]周成当,成菊安.模糊神经网络岩性识别系统[J].江汉石油学院学报,1993,15(4):40-44. ZHOU Chengdang,CHENG Ju′an.A lithology recognition system based on fuzzy neural network[J].Journal of Jianghan Petorleum Institute,1993,15(4):40-44. [3]范训礼,戴航.神经网络在岩性识别中的应用[J].测井技术,1999,23(1):50-52. FAN Xunli,DAI Hang.Applications of neural network in lithology identification[J].Well Logging Technology,1999,23(1):50-52. [4]金明霞,张超谟,刘小梅.基于MATLAB神经网络的岩性识别[J].江汉石油学院报,2003,12(4):81-83. JIN Mingxia,ZHANG Chaomo,LIU Xiaomei.Lithologic identification based on MATLAB neural network[J].Journal of Jianghan Petorleum Institute,2003,12(4):81-83. [5]罗德江,郭科.小波神经网络在致密砂岩储层参数预测中的应用[J].内蒙古石油化工,2007,27(12):119-122. LUO Dejiang,GUO Ke.Application of WNN algorithm in reservoir prediction of compact sandstone[J].Inner Mongolia Petrochemical Industry,2007,27(12):119-122. [6]怀海宁,刘建英.BP神经网络在储层物性预测中的应用:以鄂尔多斯南部镇原区块为例[J].内蒙古石油化工,2008,28(8):12-14. HUAI Haining,LIU Jianying.BP neural network in prediction of reservoir properties:A case investigation of Zhenyuan field in southern Ordos[J].Inner Mongolia Petrochemical Industry,2008,28(8):12-14. [7]张国英,王娜娜,张润生,等.基于主成分分析的BP神经网络在岩性识别中的应用[J].北京化工学院学报,2008,16(3):43-46. ZHANG Guoying,WANG Nana,ZHANG Runsheng,et al.Application of principal component analysis and BP neural net-work in identifying lithology[J].Journal of Beijing Institute of Petro-chemical Technology,2008,16(3):43-46. [8]李军梅,胡以华,陶小红.基于主成分分析与BP神经网络的识别方法研究[J].红外与激光工程,2005,34(6):719-723. LI Junmei,HU Yihua,TAO Xiaohong.Recognition method based on principal component analysis and back-propagation neural network[J].Infrared and Laser Engineering,2005,34(6):719-723. [9]杨静,毛宗源.基于PCA和神经网络的识别方法研究[J].计算机工程与应用,2007,43(25):246-248. YANG Jing,MAO Zongyuan.Recognition method based on principal component analysis and neural network[J].Computer Engineering and Applications,2007,43(25):246-248. [10]吴新生,谢益民,刘焕彬.主成分分析法用于化工过程人工神经网络建模[J].计算机与应用化学,1999,16(3):219-221. WU Xinsheng,XIE Yimin,LIU Huanbin.Application of principal components analysis in artificial neural network modeling of chemical process[J].Computers and Applied Chemistry,1999,16(3):219-221. [11]梁宾桥,王继宗,梁晓颖.高性能混凝土强度预测的神经网络-主成分分析[J].计算机工程与应用,2004,18:192-195. LIANG Binqiao,WANG Jizong,LIANG Xiaoying.Principle component analysis and neural networks for strength forecast of high performance concrete[J].Computer Engineering and Application,2004,18:192-195. [12]杨海澜,蔡艳,陈庚军.主成分分析结合神经网络技术在焊接质量控制中的应用[J].焊接学报,2003,24(4):55-58. YANG Hailan,CAI Yan,CHEN Gengjun.Principal component analysis based artificial neural networks for arcwelding quality control[J].Transactions of the China Welding Institution,2003,24(4):55-58. [13]李岳,吕克洪.主成分分析在铁谱磨粒识别中的应用研究[J].国防科技大学学报,2004,26(1):89-94. LI Yue,LÜ Kehong.The application of the principal components analysis (PCA) to debris recognition[J].Journal of National University of Defense Technology,2004,26(1):89-94. [14]范金城,梅长林.数据分析[M].北京:科学出版社,2002:142-148. [15]王学仁,王松桂.实用多元统计分析[M].上海:上海科学技术出版社,1990:270-330. (责任编辑:高丽华) Lithology Identification of Unconventional Reservoirs Based on PCA-BP Neural Network HU Jialiang1,GAO Yuchao2,YU Jifeng1,LU Lei1,ZHANG Hongjun1,YANG Ziqun1 (1.College of Earth Science and Engineering,Shandong University of Science and Technology,Qingdao,Shandong 266590,China;2.Geological Mining Construction Branch,Donghua Construction Co.,Ltd of Yankuang Group,Zoucheng,Shandong,273500,China) Lithology identification has been the key and difficult point of reservoir logging interpretation.Considering the low accuracy of conventional lithology identification methods,the BP neural network based on improved principal component analysis (PCA) was studied on the basis of logging data analysis and with Matlab as the platform.The actual logging data of unconventional reservoir in Jiyang sag was taken as sample,on which experiment simulation was performed by designing algorithm.The simulation results show that with the unconventional reservoir lithology identification rate of 95.8%,which is higher than BP neural network,PCA-BP neural network is effective to improve the identification rate and speed.The logging lithology identification in Jiyang sag proves that this lithology identification method is feasible and has practical values. unconventional reservoirs;Jiyang sag;lithology identification;principal component analysis;BP neural network 2016-02-21 国家自然科学基金项目(41472092) 胡嘉良(1989—),男,山东曲阜人,硕士研究生,主要从事地质工程等方面研究.E-mail:jialhu@126.com 余继峰(1964—),男,安徽萧县人,教授,博士生导师,主要从事能源盆地分析、测井地质定量解释、旋回地层学等方面研究,本文通信作者.E-mail:yujifeng05@163.com P631 A 1672-3767(2016)05-0009-08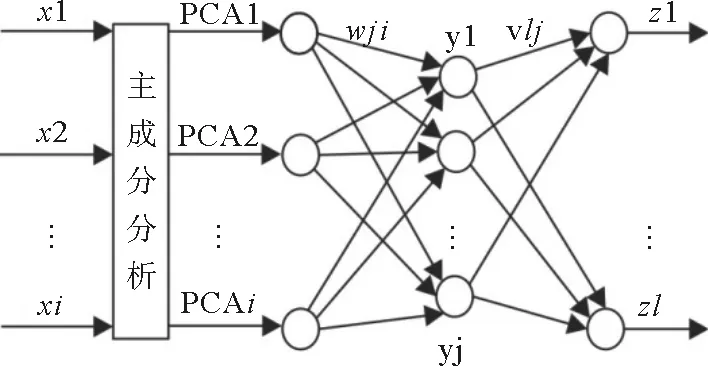
2 PCA-BP神经网络模型构建及训练






3 应用实例

4 结论

