大学物理教学中微积分知识与物理问题的衔接
周瑞雪,伍 东,贺启亮
(贵州师范大学 物电院,贵州 贵阳 550001)
大学物理教学中微积分知识与物理问题的衔接
周瑞雪,伍 东,贺启亮
(贵州师范大学 物电院,贵州 贵阳 550001)
微积分在大学物理教学中应用很多,文章主要针对微分概念和积分知识在大学物理中的应用问题的衔接方面,从物理问题应用的角度阐述了微分概念、定积分概念、曲边梯形面积的计算、求和式的极限,用微积分知识计算瞬时速度、瞬时加速度、质点运动位移时的衔接,以及用定积分知识解决其他物理问题的衔接,典型的有变力做功问题、电流激发磁场的B值计算、质量连续分布刚体的转动惯量问题等等。
微积分;物理问题;衔接
引言
在大学物理教学中,学生最先接触到的就是微积分知识在物理中的应用,有些学生在高中时学了一点微分的知识,但积分知识基本上没有学。进入大学后,在高等数学这门课程的学习中会学到微积分的知识内容,但往往学了以后也是数学是数学的,物理是物理的,在开始大学物理这门课程的学习时不怎么会把数学知识和物理问题衔接起来,也不会很快把数学中学到的知识应用到物理学中来,不会融会贯通,因此有必要将微积分知识与物理问题的衔接详述如下。
1 数学中的微分概念与物理中瞬时速度瞬时加速度概念的衔接
1.1 问题的提出和解决
从上面看出,解决物理问题变成了用数学的求导数方法来计算,为什么?
1.2 数学中导数的定义
设函数y=f(x)在x=x0处有增量Δx,与此相应,函数y也发生一增量Δy,
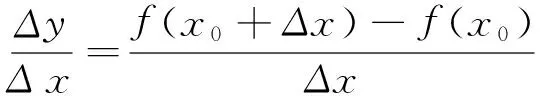
叫作函数y=f(x)在x到x+Δx之间的平均变化率。
(1)
以上是数学中定义导数的概念
1.3 物理学中瞬时速度和瞬时加速度的定义
瞬时速度可看作在某一很短很短时间内的平均速度,即Δt→0时的平均速度,瞬时加速度同样也是Δt→0时的平均加速度,公式可写成如下:
(2)
(3)
1.4 导数的计算与瞬时速度和瞬时加速度计算的衔接
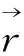
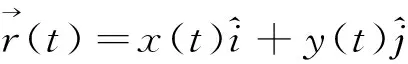
2 数学中定积分概念与计算质点运动位移问题的衔接
2.1 问题的提出和解决
某质点做下列三种运动:①匀速直线运动;②匀变速直线运动;③变速直线运动;分别计算时间从t到t+Δt时刻质点的位移Δx=?。已知初速度为v0,初始位置为x0
①质点做匀速直线运动的位移Δx=v0Δt由匀速运动的v-t图像(图1)可知位移的大小可等于图中阴影部分面积。

图1
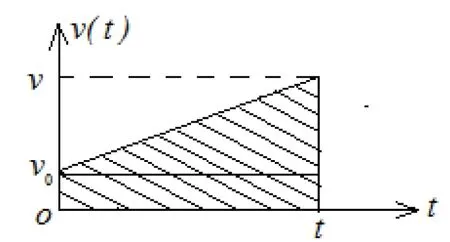
图2
③ 质点做变速直线运动的位移怎样计算呢?
由于变速运动的速度不断改变,我们可把它分为无数多个时间很短的运动,时间很短的情况下速度变化不大,可近似看作是匀速运动,匀速运动的位移大小等于v-t图像下面的矩形面积。
如图3我们可把此曲边梯形划分为无数多个小长条,而其中的小长条面积可看成一个时间很短近似于质点匀速运动的位移,那么全部小长条面积加起来即是此曲边梯形的面积,此曲边梯形的面积的大小即是质点做变速直线运动的位移。
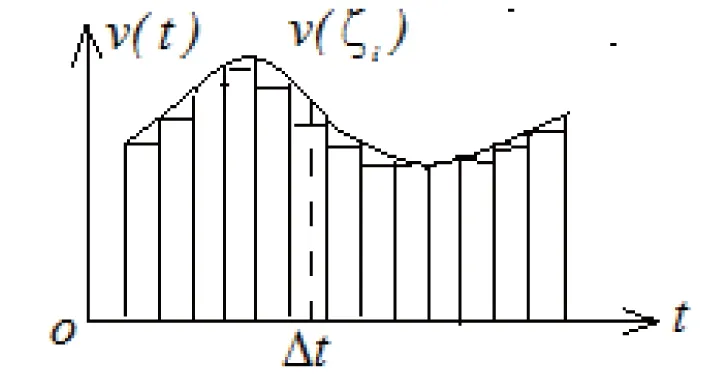
图3
2.2 数学中的定积分概念
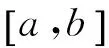
(4)
2.3 关于曲边梯形的面积和物体运动的位移
2.3.1 曲边梯形的面积:如图4

图4

图5
由y=f(x)的函数曲线以及直线x=a、x=b和x轴所围成的图形叫作曲边梯形,
(5)
从(5)看出,和式的极限能够精确地描述曲边梯形的面积ΔS
2.3.2 物体运动的位移
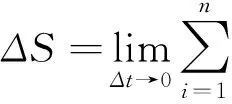
(6)
由(6)看出,和式的极限能够精确描述质点的位移ΔS。
(5)、(6)都是和式的极限,定义为积分,将 (4)式与(5)、(6)式比较,可知物体运动的位移即是曲边梯形的面积,用Δx表示质点运动的位移、x(t)表示质点的运动方程,x0表示质点运动的初位置,得到:
由此得出,若已知质点运动的速度与时间的函数关系及初始条件,可用积分的方法计算出质点运动的位移及运动方程。
3 定积分知识解决其他物理问题的衔接
前面所述,在已知质点作变速运动的速度函数关系和初始条件下,应用定积分知识可计算出质点运动的位移,定积分知识除了能解决上述问题,还能解决物理中的好多问题。
3.1 变力做功问题
如图6 若质点在一随时间变化的变力F(t)作用下沿曲线运动而不是直线运动,需要计算此变力从A到B对质点做功的表达式。



图6

图7
3.2 质量连续分布刚体的转动惯量问题


3.3 电荷连续分布的带电体的电场强度和电势


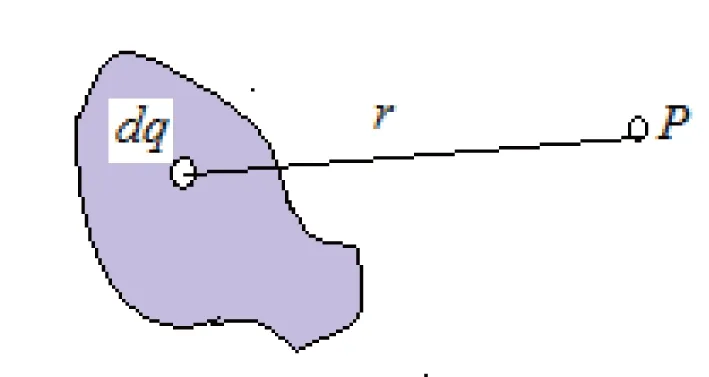
图8
整个带电体在P点激发的电场强度和电势即是每个电荷元激发的电场强度和电势的叠加,那问题又归结为求和式的极限,即数学中的定积分计算。
3.4 电流激发磁场的B值计算
导线通以电流时,在其周围要产生磁场,把一载流导线看成是由许多个电流元连接而成,这样,载流导线在磁场中某点所激发的磁感强度B就是由这导线的所有电流元在该点产生磁场dB的叠加,这就又归结为求和式的极限,即数学中的定积分计算,如图9。
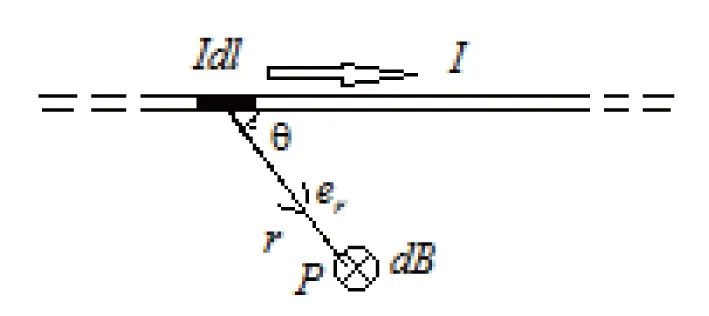
图9
3.5 载流导线在磁场中所受安培力的计算
对于一长直载流导线放在如图10所示的磁场中时,其所受安培力大小为 F=BIL,前提条件是场是均匀磁场且方向与电流方向垂直,F的方向垂直于磁场方向与电流方向组成的平面。但如果磁场不是均匀场,载流导线不是直导线,则弯曲导线所受的安培力该怎样计算?

图10

图11
如图11,可将弯曲的载流导线分成无数多个小段,每一小段载流导线受到的安培力叠加起来即是整个弯曲导线受到的力,问题又归结为求和式的极限,即数学中的定积分计算。
除了上面所述问题,物理学中还有很多用定积分知识解决的问题,如变力产生的冲量的计算问题、导线在磁场中切割磁力线产生感生电动势问题计算、全电流安培环路定理、刚体力学中力矩作功问题、热学中热温比的积分等于熵增加问题,等等,这里不再一一赘述。微积分知识在物理学中应用很广,知识衔接很重要。衔接好了,对物理问题的解决就会融会贯通,达到事半功倍的效果,在大学物理的教学中对于学生的知识理解有很大的帮助。
[1]东南大学.物理学(上册)第五版[M]. 北京:高等教育出版社,2006.
[2]F.W.sears . 大学物理学(第一册)[M].郭泰运,译.北京:人民教育出版社,1979.
[3]漆安慎,杜婵英.力学[M].北京:高等教育出版社,2005:281-297.
[4]徐德,刘聚成,袁贞丰.大学物理学习题解答[M]. 北京:人民教育出版社,1989.
[5]周衍柏.理论力学. [M]. 北京:人民教育出版社,1982.
[6]华东师范大学数学系.数学分析(上册)第三版[M]. 北京:高等教育出版社.
The Connection between Calculus Knowledge and Physical Problems in College Physics Teaching
ZHOU Rui-xue,WU Dong,HE Qi-liang
(School of Physics and Electronics,Guizhou Normal University,Guiyang,Guizhou 550001 China)
Calculus is widely applied in college physics teaching, In this paper, we mainly aimed at the connection of the differential concept and the application of the integral knowledge in college physics, and mainly elaborated the concept of the differential concept and the definite integral, the calculation of curved edge trapezoid area, and the limit of the sum, using calculus knowledge to calculate instantaneous velocity and instantaneous acceleration, particle motion displacement connecting, and solving other physics problem connecting by definite integral knowledge, such as variable force-work problem, B value calculation of current induced magnetic field, moment of inertia of continuous mass distribution of rigid body, etc.
Calculus; Physical Problems; Connection
2016-04-25
国家自然科学基金:“环境噪音下腔QED的量子关联”(项目编号:11364006);贵州省科学技术基金:“基础物理学问题专题研究” (项目编号:黔科合J字LKS[2013]12号)。
周瑞雪(1963-),女,贵州毕节人,副教授。主要研究方向:基础物理学、量子物理学。 伍 东(1957-),男,四川成都人,高级工程师。主要研究方向:电子物理及通信工程。 贺启亮(1982-),男,贵州遵义人,副教授、博士。主要研究方向:量子关联和量子信息研究。
G64
A
1673-6125(2016)03-0064-05

