基于模糊自适应滑模变结构的PWM整流器

顾华利，张开如，狄东照，樊英杰，王毅，李娅芸

（1.山东科技大学电气与自动化工程学院，山东青岛 266590；2.山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地，山东青岛 266590）

基于模糊自适应滑模变结构的PWM整流器

顾华利1，2，张开如1，2，狄东照1，2，樊英杰1，2，王毅1，2，李娅芸1，2

（1.山东科技大学电气与自动化工程学院，山东青岛 266590；2.山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地，山东青岛 266590）

为了提高三相电压型PWM整流器（VSR）的抗扰能力，通过分析三相VSR的数学模型，提出了基于同步旋转d-q坐标系的模糊自适应滑模变结构控制算法。该算法考虑到传统双闭环PI的缺陷性，将外环设置为模糊控制器和滑模变结构控制器相结合，利用模糊控制规则实时调整滑模趋近律，在提高系统鲁棒性的同时又能削弱滑模面上的抖振；内环将PI控制改为比例控制，简化系统结构。小波分析和MATLAB分析运行数据结果表明，基于模糊自适应滑模控制的三相VSR系统相对于传统双闭环PI系统具有更强的动态性能和跟踪能力。

电压型PWM整流器（VSR）；模糊自适应；滑模变结构；小波分析

三相电压型PWM整流器（VSR）因其具有能够实现单位功率因数控制、能量双向传输等优点，而广泛应用在电力工业中[1]。三相VSR本身为非线性、不确定系统，传统双闭环PI控制器虽然结构简单、易于数字化，但其本身易受到外部扰动及自身参数变化的影响[2]。一旦受到不确定因素的影响，将导致三相VSR系统的鲁棒性和动态性能变差，因此常规的控制策略很难达到理想的控制效果[3-4]。

目前，智能控制如模糊控制、神经网络控制等被应用于三相VSR控制系统中[5]。由于模糊控制规则之间的相互作用，单纯使用模糊控制难以达到理想效果。神经网络虽然具有容错性、非线性逼近的优点，但神经控制器在运行过程中需要边学习边调整权值，因此对微处理器提出了较高的要求，难以数字化实现[6]。滑模控制是一种变结构系统控制的非线性控制方法，该控制方法根据系统状态变量在状态空间中的当前位置以高频在一个结构和另一个结构之间切换，迫使被控制系统能够精确地跟踪预先设定的期望值[7-9]。一旦系统进入预先设定的滑动模态，对外部扰动及不确定因素具有很强的鲁棒性[10-12]。但滑模控制会使系统以极高的频率切换，导致系统出现有害的抖振效应。20世纪80年代在滑模控制引入准滑模动态和边界层的概念，即在边界层外采用正常的滑模控制，在边界层内采取连续反馈控制，这种方法可以有效削弱抖振，但这种方法以牺牲控制精度为代价，给控制系统带来误差[13]。在外环采用模糊控制和滑模控制相结合的方式在线调整滑膜趋近律，来提高系统的鲁棒性，减弱滑模控制在滑膜面上的抖振效应，加快响应时间，保证控制精度。内环将2个PI控制器设置为比例P控制器，简化系统结构。

本文采用模糊控制和滑模控制相结合的复合控制方案，结合两者的优点来提高三相VSR的抗干扰能力和动静态性能，减少抖振引起电力电子开关器件的损耗。通过仿真证明了模糊自适应滑模控制的三相VSR系统比传统双闭环PI系统具有更强的鲁棒性。

1 三相VSR数学模型

如图1所示为三相VSR的一般拓扑结构。图1中，VT1-VT6为IGBT；VD1-VD6为反并联的二极管；ea、eb、ec为电网电动势；ua、ub、uc为三相桥臂输入端相对电网中性点电压；ia，ib，ic为三相输入电流；L为输入滤波电感；Rs为系统等效内阻；电阻RL为直流侧负载；iL为负载电流；C为滤波电容；Vdc为直流侧电压。根据基尔霍夫电压定律得到三相VSR在静止坐标系下的状态方程为：

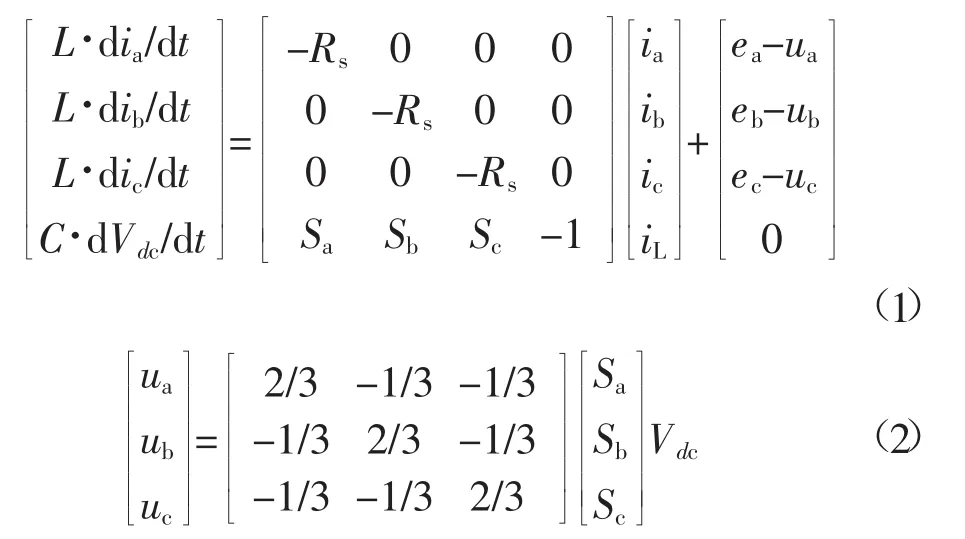
式中：Si（i=a，b，c）表示三相VSR每一桥臂的开关状态，Si=1表示上桥臂导通下桥臂关断，Si=0则表示相反。两相静止坐标系（Clark）变换和两相静止坐标系到两相旋转坐标系（Park）变换，可以得到在d-q坐标系下的状态方程为：

式中：ed、eq，ud、uq，id、iq分别为电网电动势，整流器输入电压，输入电流在d-q坐标轴的分量；ω为旋转角频率。

由式（3）可知，在d-q坐标系下两相电流之间相互耦合，故电压方程是非线性的。因此采用简单线性PI控制不能体现三相VSR的非线性本质，使系统的控制性能受到限制。如图2所示为模糊自适应滑模控制原理图，将电压外环改为模糊滑模控制，内环2个PI控制器改为比例P1、P2控制器，提高系统的抗干扰能力。

图1 三相电压型PWM整流器拓扑结构Fig.1 Topology of the three-phase voltage-source PWM converter

图2 模糊自适应滑模控制结构图Fig.2 Block scheme of the fuzzy adaptive sliding mode variable structure

2 控制器设计

滑模控制分为2个阶段，即到达阶段和滑动阶段。

如图3（a）为滑模控制运动到达阶段，系统状态变量从任意位置趋近轨线S。如图3（b）所示为理想情况下的滑动阶段，即系统进入轨线S，沿着滑模面滑动到O点，此时系统运行状态与外部扰动和不确定因素无关，具有自适应性和很强的鲁棒性。滑动阶段所需要时间通常大于到达阶段时间，因此控制系统设计时仅考虑滑动阶段即可。这2种状态存在的条件必须满足李雅普诺夫稳定性原理，即S满足：

式中：S为滑模面。三相VSR控制的量有3个，从图2中可以看出即为其中由和Vdc的差值计算而来，因此针对2个量设计开关函数即可，即系统开关滑动模态的开关线有2条。令ev、ei、dVdc/dt、diq/dt作为状态变量。则令系统的开关函数为：

图3 滑模控制Fig.3 Sliding mode control

根据劳斯赫尔维兹判据，式（6）特征方程具有负实根稳定的必要条件为特征方程各项系数为正，因此k1＞0、k2＞0。

将ev、ei表达式代入式（6）可得：

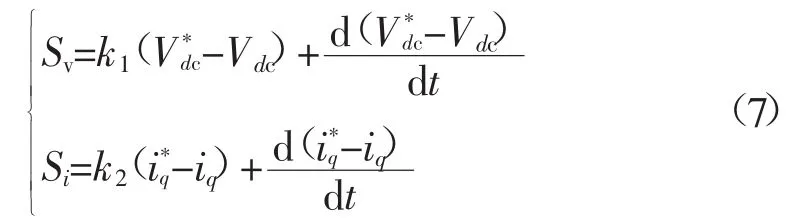
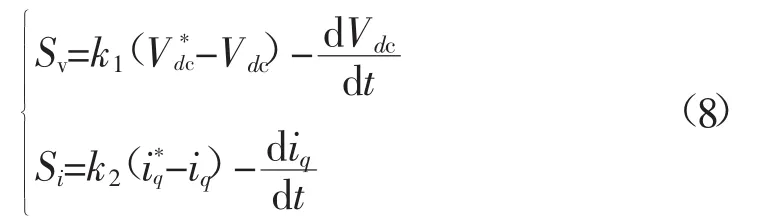
将式（3）、式（4）代入式（8）可得：

再对式（4）变形可得：

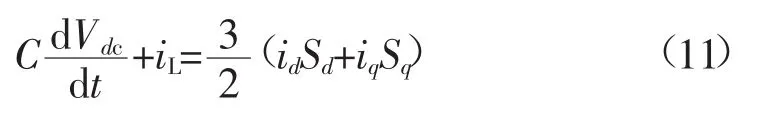
两边同乘以Vdc可得：

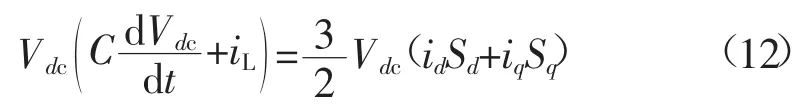
式（12）左边即为三相VSR的输出功率。若忽略三相VSR自身等效电阻等因素，则有：

联立式（9）、式（11）—式（13）可得：

当系统运行到稳定状态时did/dt=diq/dt=0，则由式（3）可知：

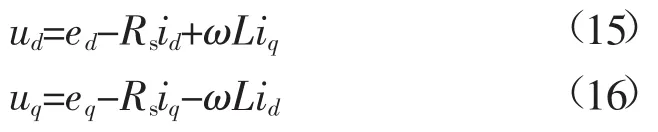
同时d轴电压与电网电压同向，因此eq=0，将式（15）、式（16）代入式（14），并忽略系统自身等效内阻Rs，化简可得:

两边同除以ed/CVdc，并令k=k1CVdc/ed，则式（17）变为：

再把式（16）代入式（10）可得：

因此结合式（18）、式（19）可将系统2条滑膜开关线等效为：

其中等效控制量为：

为了满足式（5）条件，当Sv＞0时，则因此应增大id，由式（3）可知应减小ud。同理，当Sv＞0时，应增大ud。当Si＞0时，则因此应增大iq，同样由式（3）可知应减小uq。同理当Si＞0时，应增大uq。

如图4所示，考虑到id、iq的解耦，选择简单的比例控制P1、P2即可满足要求，控制方程为：

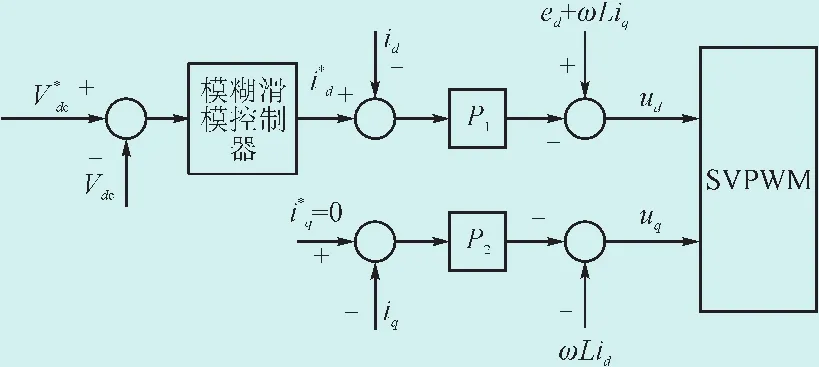
图4 模糊自适应滑模控制框图Fig.4 Block diagram of fuzzy adaptive sliding mode variable structure

当系统进入预先设定好的滑模面后，虽然对外界干扰因素不敏感，满足稳定性条件，但并不能反映出系统在滑模面上的运动情况。抖振产生的原因是到达开关线的速度过大，开关控制力有限，使运动难以反向，造成在开关线附近来回切换形成抖振，对机械造成损害，因此必须控制滑模趋近律来削弱抖振。合适的趋近律可以保证系统在滑模面上的正常运动品质，当远离滑模面时，可以提高系统向滑模面的运动速度，来加快系统响应速度；当靠近滑模面时，减小系统向滑模面的运动速度，避免抖振带来的损害。

由S1=k1ev+dev/dt=0变形可得：

对式（23）等速趋近律等式解微分方程可得：

因此跟踪误差将以指数的形式收敛，根据指数的收敛性质，可通过V*dc-Vdc的差值来调整k1的大小，进而调整滑模趋近律。

如图5所示将电压差ev、电压差的导数dev输入二维模糊控制器中，输出的d（Δk1）乘以量化因子KΔ1得到Δk1来实时调整滑模控制器中k1的大小，使系统在滑模面上有良好的运动性能，削弱抖振。

图5 k1的实时调整Fig.5 Real-time adjustment of k1

如图6所示d（Δk1）含7个模糊子集{NB（负大），NM（负中），NS（负小），ZO（零），PS（正小），PM（正中），PB（正大）}，连续性论域为[-6，6]。模糊化和去模糊化采用三角形隶属函数，去模糊化采用加权平均法。d（Δk1）的控制规则如表1所示。

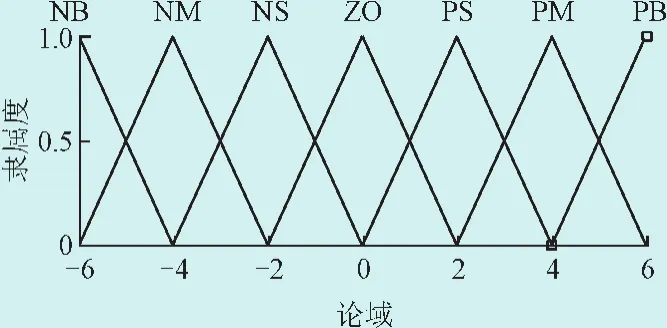
图6 d（Δk1）的隶属函数Fig.6 Membership function of d（Δk1）

表1 d（Δk1）的模糊推理规则表Tab.1 Fuzzy inferential rules of d（Δk1）

根据模糊规则得到的3D效果图如图7所示。

图7 比例系数d（Δk1）Fig.7 The proportional coefficient d（Δk1）

即通过模糊规则表得到d（Δk1）的范围，进而与量化因子KΔ1乘积得出Δk1来修改初始值k1，进而调整滑模趋近律。

3 仿真结果

采用MATLAB/SIMULINK搭建模糊自适应滑模三相VSR和传统双闭环PI控制仿真模型。网侧输入的三相交流电压为160 V，输入电流峰值为20 A，频率50 Hz。输出直流电压为270 V，电容C为3 200 μF，电感L为6.5 mH，负载电阻RL为18 Ω。系统中含有3个PI调节器，经过模型参数计算可得，双闭环PI电压调节器参数设置为Kp=0.378、Ki=15.68；电流调节器参数设置为Kp=1.54、Ki=118.5；模糊自适应滑模模型中P1=P2=1.54、量化因子KΔ1=20；三相VSR的开关频率为10 kHz。

如图8所示，当系统稳定运行时电网侧电压与电流同频同相，即电网侧向负载传输有功功率。如图9所示，系统进入稳定状态时功率因数值达到0.996以上，接近于单位功率因数值1，满足国家标准规定，证明了模糊自适应滑模控制系统的正确性。

图8 交流侧侧电压和电流波形Fig.8 AC side voltage and current waveform

图9 功率因数图Fig.9 Power factor diagram

在0.4 s时刻系统突加负载，如图10所示为2种不同控制策略下的直流侧输出电压波形图。由图11（a）可知，模糊自适应滑模控制方式比双闭环PI控制具有更小的超调量，且能够更快到达稳态值。由图11（b）可知，模糊自适应滑模控制方式比双闭环PI控制波动范围小，恢复到稳态值时间短。由小波分析包抽取11（a）、图11（b）2个图数据（精确到小数点后两位）并行计算，如表2所示。

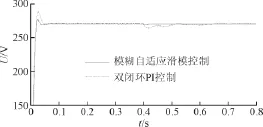
图10 直流侧电压波形Fig.10 DC side voltage waveform

系统输出电压的给定稳态值为270 V，由表2可知，双闭环PI控制电压超调量为6.46%小于10%，且由图10知到达稳态值时间小于0.1 s，均满足控制系统性能指标，即原系统参数设计是有效的、合理的。而模糊自适应滑模控制的超调量为2.56%，说明该控制方式可有效优化系统性能，降低超调量。当负载发生突变时，双闭环PI控制电压波动范围大，最大电压波动差值达到6.48 V，由图11（b）恢复到稳态值所需时间为0.22 s。而模糊自适应滑模控制电压波动差值小，仅为1.38 V，且恢复到稳态值的时间短仅需0.05 s，比双闭环PI控制提前了8.5个基波周期，即该控制方式具有更强的抗干扰能力和动态性能。为进一步对比2种系统的性能，采用sym8小波抽取0～1 s仿真数据构成电压分布柱状图，如图12所示。

图11 直流侧电压对比图Fig.11 DC side voltage differences

表2 2种控制方式的电压数据对比Tab.2 Voltage data contrast between two control modes

对比图12（a）、图12（b）电压分布柱状图可知，双闭环PI控制方式电压值为270 V，占所有抽取数据的38.274%，2侧分布电压所占比例较大，说明双闭环控制方式抗扰能力较差，电压波动范围大。模糊自适应滑模控制方式输出直流侧电压稳定，其中电压值为270 V，占所有抽取数据的91.168%，两侧分布电压所占的百分比小，即模糊自适应滑模控制系统具有更好的鲁棒性。

图12 电压分布柱状图Fig.12 Distribution histogram of voltage

4 结语

本文将模糊自适应滑模控制应用到三相VSR中，电压外环采用模糊控制器与滑模控制器相结合的方式，利用模糊规则来调整趋近律，提高系统在滑模面上的运动品质；内环选择2个简单的比例控制器。2种方式相结合，既能提高系统的鲁棒性，又能加快系统的响应速度。通过仿真证明模糊自适应滑模控制相对于传统PI控制具有更强的抗干扰能力和动态性能。

[1]程启明，程尹曼，薛阳，等.三相电压源型PWM整流器控制方法的发展综述[J].电力系统保护与控制，2012，40（3）:145-155.CHENG Qiming，CHENG Yiman，XUE Yang.A summary of current control methods for three-phase voltage-source PWM rectifiers[J].Power System Protection and Control，2012，40（3）:145-155（in Chinese）.

[2]朱志键，王杰.三相电压型PWM整流器的二自由度内模控制[J].电网与清洁能源，2015，31（11）.ZHU Zhijian，WANG Jie.Two degrees of freedom internal model control of the three-phase voltage-sourced PWM retifier[J].Power System and Clean Energy，2015，31（11）（in Chinese）.

[3]彭咏龙，张晶，王宇，等.三相电流型PWM整流器的SVPWM调制方法研究[J].华北电力大学学报:自然科学版，2009，36（2）:28-32.PENG Yonglong，ZHENG Jing，WANG Yu，et al.Research of space vector modulation methord for three phase current source rectifier[J].Journal of North China Electric Power University（Natural Science Edition），2009，36（2）:28-32（in Chinese）.

[4]赵仁德，贺益康，刘其辉.提高PWM整流器抗负载扰动性能研究[J].电工技术学报，2004，19（8）:68-72.ZHAO Rende，HE Yikang，LIU Qihui.Research on improvement of anti-disturbance performance for threephase PWM rectifiers[J].Transaction of China Electrotechnical Society，2004，19（8）:68-72（in Chinese）.

[5]严干贵，齐磊，李军徽，等.三相电压型整流器反馈线性化解耦系统的Pl控制器参数整定[J].南方电网技术，2009，3（5）:103-106.YAN Gangui，QI Lei，LI Junhui.PI controller parameters setting of the three-phase decoupling feedback linearization VSR system[J].Southern Power System Technology，2009，3（5）:103-106（in Chinese）.

[6]陈瑶，金新民，童亦斌.基于滑模控制的三相电压型PWM整流器系统仿真[J].系统仿真学报学报，2007，19（8）:1849-1852.CHEN Yao，JIN Xinmin，TONG Yinbin.Simulation of three-phase voltage source PWM rectifier based on slidingmode control[J].Journal of System Simulation，2007，19（8）:1849-1852（in Chinese）.

[7]贾宇辉，李剑林，王孝洪，等.PWM整流器滑模变结构控制算法研究[J].电测与仪表，2011，48（7）:7-11.JIA Yuhui，LI Jianlin，WANG Xiaohong.Study on sliding-mode variable structure control algorithm for PWM rectifer[J].Electrical Measurement and Instrumentation，2011，48（7）:7-11（in Chinese）.

[8]樊英杰，张开如，马慧，等.基于模糊PI永磁同步电机优化矢量控制系统的研究[J].电气传动，2016，46（3）: 15-19.FAN Yingjie，ZHANG Kairu，MA Hui，et al.Study of permanent magnet synchronous motors optimized vector control system based on fuzzy PI controller[J].Electric Drive，2016，46（3）:15-19（in Chinese）.

[9]黄凯征，汪万伟，王旭.基于滑模控制的PWM整流器建模与仿真[J].电网技术，2009，33（8）:18-23.HUANG Kaizheng，WANG Wanwei，WANG Xu.Modeling and simulation of PWM rectifier based on slidingmode control[J].Power System Technology，2009，33（8）: 18-23（in Chinese）.

[10]顾华利，张开如，狄东照，等.基于模糊自整定PI永磁同步电机矢量控制系统的研究[J].电力科学与工程，2016，32（5）:14-19.GU Huali，ZHANG Kairu，DI Dongzhao，et al.Study of permannet magnet synchronous motor system based on fuzzy self-turning PI[J].Electric Power Science and Engineering，2016，32（5）:14-19（in Chinese）.

[11]李鹏，马建军，李文强，等.一类不确定非线性系统的改进积分型滑模控制[J].控制与决策，2009，24（10）: 1463-1472.LI Peng，MA Jianjun，LI Wenqiang，et al.Improved integral sliding mode control for a class of nonlinear uncertain systems[J].Control and Decision，2009，24（10）: 1463-1472（in Chinese）.

[12]韩俊，徐政，李侠.基于PSCAD/EMTDC的24脉波整流器模型研究[J].高压电器，2010，46（12）:18-21.HAN Jun，XU Zheng，LI Xia.Research on 24-pulse rectifier model based on PSCAD/EMTDC[J].High VoltageApparalus，2010，46（12）:18-21（in Chinese）.

[13]樊英杰，张开如，韩璐，等.基于优化SVPWM三相VSR的仿真与研究[J].电测与仪表，2015（12）:40-45.FAN Yingjie，ZHANG Kairu，HAN Lu，et al.Simulation and study of three-phase voltage-souece rectifier（VSR）base on an optimized SVPWP[J].Electrical Measurement and Inctrumentatoin，2015（12）:40-45（in Chinese）.

张开如（1957—），教授，研究方向为电力电子与电力传动、电力系统及其自动化；

狄东照（1990—），硕士研究生，研究方向为电力电子技术及应用；

樊英杰（1990—），硕士研究生，研究方向为控制理论与控制工程；

王 毅（1978—），女，讲师，博士研究生，研究方向为现代电力电子变换技术及应用；

李娅芸（1990—），硕士研究生，研究方向为电力电子技术及应用。

（编辑 董小兵）

The PWM Rectifier Based on Fuzzy Adaptive Sliding Mode Variable Structure

GU Huali1，2，ZHANG Kairu1，2，DI Dongzhao1，2，FAN Yingjie1，2，WANG Yi1，2，LI Yayun1，2
（1.College of Electrical Engineering and Automation，Shandong University of Science and Technology，Qingdao 266590，Shandong，China；2.State Key Laboratory of Mining Disaster Prevention and Control Co-Founded by Shandong Province and the Ministry of Science and Technology，Shandong University of Science and Technology，Qingdao 266590，Shandong，China）

In this paper，a fuzzy adaptive sliding mode variable structure control algorithm based on synchronous rotating reference frame is presented through analyzing the mathematical model of three-phase voltage-source PWM rectifier（VSR），which aims to improve the anti-interference performance.Considering the defects of traditional PI controller，this paper proposes a method which combines the fuzzy controller with sliding mode variable structure controller，utilizes fuzzy control rules to adjust the sliding mode reaching law on-line for outer voltage loop so that the robustness of the system can be improved while the vibration on the sliding surface be minimized.And the inner loop PI controller is changed to the proportional controller to simplify the system structure.The wavelet analysis and MATLAB simulation of the running data suggest that the three-phase voltage-source PWM rectifier based on fuzzy adaptive sliding mode variable structure system is superior to the conventional PI control system in the dynamic stability and speed tracking ability.

the voltage-source PWM rectifier（VSR）；fuzzy adaptive；sliding mode variable structure；wavelet analysis

“十二五”国家科技支撑计划项目（2012BAB13B04）；国际（中国-南非）科技合作项目（CS06-L02）。

Project Supported by the National Twelfth-Five Year Research Program of China（2012BAB13B04）；International Science and Technology Cooperation Project between China and South Africa（CS06-L02）.

1674-3814（2016）08-0040-06

TM461

A

2015-12-11。

顾华利（1990—），男，硕士研究生，研究方向为电力系统及其自动化；