分级加载条件下的锯齿状结构面剪切松弛特性

田光辉，沈明荣,2，周文锋，李彦龙，刘之葵

(1.同济大学 土木工程学院，上海200092；2.岩土及地下工程教育部重点实验室(同济大学)，上海200092；3.平顶山市公路管理局，河南 平顶山467000； 4.桂林理工大学 土木与建筑工程学院，广西 桂林541004)



分级加载条件下的锯齿状结构面剪切松弛特性

田光辉1，沈明荣1,2，周文锋1，李彦龙3，刘之葵4

(1.同济大学 土木工程学院，上海200092；2.岩土及地下工程教育部重点实验室(同济大学)，上海200092；3.平顶山市公路管理局，河南 平顶山467000； 4.桂林理工大学 土木与建筑工程学院，广西 桂林541004)

为研究结构面的剪切应力松弛特性，采用水泥砂浆浇筑成不同角度的结构面试样，利用岩石双轴流变试验机对规则齿形结构面进行不同剪切应力水平下的松弛试验，试验结果表明：结构面剪切应力松弛曲线可以分为瞬时、减速和稳态3 个阶段；依据松弛曲线特征，考虑模型参数的时间相关性，将粘滞系数看作是与时间有关的非定常参数，建立非线性Maxwell松弛方程，与试验曲线拟合结果比较理想，得到了初始粘滞系数与剪应力水平的关系；根据松弛应力随剪应力水平的变化规律，及蠕变确定长期强度的机理，提出了应力松弛试验确定长期强度的方法，即松弛应力峰值对应的剪应力为结构面的长期强度.关键词: 结构面；剪切应力；应力松弛；非线性Maxwell松弛方程；长期强度

流变是岩石的重要力学特性之一，蠕变、应力松弛与长期强度是流变特性研究的重要方面.目前国内外的研究大多集中在岩石蠕变方面，而且在理论与实践上已经取得了一定成果[1-2].然而，工程实践当中，应力松弛现象在岩体工程中普遍存在，例如巷道、地下工程及挡土墙等等，常常因岩石的应力松弛而导致破坏[3].在岩石松弛方面，尽管人们已经认识到岩石应力松弛特性研究的重要性，但由于应力松弛试验采用变形恒定的实验控制方式，在早期的一般实验机中较难实现，应力松弛试验研究相对较少[4].早期岩石的应力松弛试验研究，主要集中在盐岩以及硬岩岩爆方面[5-11]，近期有学者对其他种类的岩石进行单轴及三轴压缩应力松弛试验研究，建立考虑松弛损伤及非定常参数的本构模型[12-17].这些研究成果主要集中在岩石的应力松弛特性方面，而在实际工程中，遇到的岩石往往是不完整的，是存在各种结构面的岩体.文献[18-19]分别采用等剪应力循环加载法和分级加载法对水泥砂浆浇筑成的Barton曲线结构面和规则齿形结构面进行了松弛试验研究.由于天然结构面的性质复杂，影响因素较多及实验前很难对结构面分布规律、发育程度、表面特征等参数进行定性和定量的描述，相关研究成果较少.结构面的存在是造成了岩体工程性质的不连续、各向异性和不均一性的根源，这些岩体结构面很大程度上控制着岩体工程的稳定性.因此在岩体工程稳定性研究中，岩体结构面松弛特性研究变的极为重要.

本文主要对松弛条件下的结构面剪切应力进行试验研究，通过常规剪切试验，获取力学参数，在对结构面松弛试验结果分析的基础上，阐述结构面的松弛规律，并采用非线性Maxwell松弛模型对实验曲线进行拟合，基于蠕变确定长期强度的机理，提出了应力松弛试验确定长期强度的方法.为减少天然结构面复杂性和不确实性，更好的研究结构面松弛规律，本文采用水泥砂浆试件浇筑的规则齿形结构面模拟天然岩体结构面.

1 试验材料与试验方法

1.1 试验设备

试验在同济大学长春CSS-1950 岩石双轴流变试验机上完成，利用自带软件系统通过伺服电机控制试验过程，自动采集试验数据，按试验要求设定采集精度.试验机可同时施加垂直轴向荷载和水平轴向荷载，也可分别施加，最大垂直轴压力500 kN、水平轴压力300 kN.可以同时测量试样双轴双侧变形值，变形量测范围为±3 mm，变形测量精度0.001 mm，能够满足试验精度要求.

1.2 试件制备

由于天然结构面形态的复杂性及其充填物性质巨大差异性，会造成试验结果离散性较大，增加分析难度.因此，为减少结构面复杂程度及保持其相对均一性，本次试验采用规则齿形结构面的水泥砂浆试件，针对结构面的松弛特性进行基础试验研究.为了避免因试件材料不同造成试验结果的差异，试件采用相同的材料、配合比、养护时间和模子.试件规格：10 cm×10 cm×10 cm，规则锯齿状结构面单齿长度10 mm，齿型个数10，采用10°、30°、45°三种角度的爬坡角(平面图见图1).模型材料选用32.5R水泥、标准砂和水，其配合比为水∶水泥∶砂=1∶2∶4.进行浇筑时，材料按配合比混合搅拌均匀，在钢模中捣实后抹平表面，尽量减少试件制作过程中的不良影响.模型成形后24 h 拆模，养护28 d.

1.3 试验方法及加载方式

本次试验为结构面的松弛试验，采用分级加载方式.试验时法向应力按完整立方体试件单轴抗压强度的10%和30%施加，并始终保持不变，剪应力分别为相同法向应力下各爬坡角结构面抗剪强度τmax的40%、60%、80%、90%、95%.通过完整立方体试件单轴抗压试验，得到其单轴抗压强度为19.62 MPa.松弛试验加载时,先施加法向应力至预定值(1.962 MPa和5.886 MPa)，待变形稳定后施加剪切应力，试验过程中法向应力恒定；施加剪应力至抗剪强度τmax的40%，保持此时产生的变形不变，观察剪应力松弛情况，试验机软件自动采集应力值大小，时间为72 h，之后按上述设定逐级提高剪应力大小.试验过程中，保持室内温度基本恒定.试验装置见图2.

图1 规则齿型结构面试件平面示意

2 试验数据及结果分析

本次结构面剪切应力松弛试验共施加5级应力水平，历时360 h，经过数据整理，得到如图3、4所示的应力松弛曲线和松弛速率曲线.

从图3、4的结构面松弛过程曲线及应力松弛速率曲线，可以看出本次结构面应力松弛试验有如下基本特征：

1)结构面的松弛发展过程可分为3个阶段：第1阶段瞬时松弛，剪应力快速降低，松弛速率较大，时间短.而且爬坡角越大，松弛速率越大，其机理可以解释为：法向应力相同时，结构面爬坡角越大，积累的变形能越大，当变形受到约束时，能量释放的速度越快，应力松弛速率越大，在几分钟内即可完成；第2阶段减速松弛，松弛速率随时间逐渐衰减.岩石内部结构调整使积累的能量逐步得到释放，松弛速率逐渐减小.持续时间1到10 h不等，结构面爬坡角越大，持续时间越长；第3阶段稳态松弛，松弛速率经历了由快到慢的过程，该阶段岩石内外作用力趋于平衡，松弛速率基本恒定，趋于常数，而且持续时间较长.

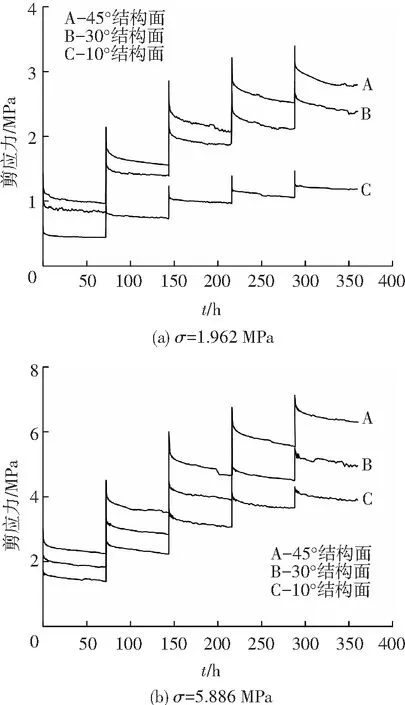
图3 不同法向应力下结构面松弛曲线

Fig.3 The relaxation curves ofdiscontinuities with different normal stress

2) 由图3、4可以清晰看出松弛试验中应力随时间的发展过程：松弛试验一开始，应力瞬时降低，且速率大，历时短，随时间的增加，松弛速率逐渐减小并趋近于零，历时时间较长，因此剪切应力的松弛曲线是一条随时间增长应力逐渐减小的非完全衰减型曲线.而且结构面在经历瞬时松弛、减速松弛和稳态松弛3个阶段后，均未出现如文献[20]中所提到的整体性破坏，即剪切应力急剧降低，持续时间很短.这是松弛和蠕变不同的地方，原因在于蠕变试验时试件所受的外力是常量，不会因试件变形而有所减小，试件开裂只会加剧内部应力集中，加速试件破坏.而松弛试验时尽管试件出现裂隙，但由于没有外部作用力对试件持续做功，试件产生的裂隙一定程度上缓解了应力集中现象，因此，一般情况下，试件仍具有一定的支撑强度，并能在很长的时间内保持静力平衡，不会产生破坏.

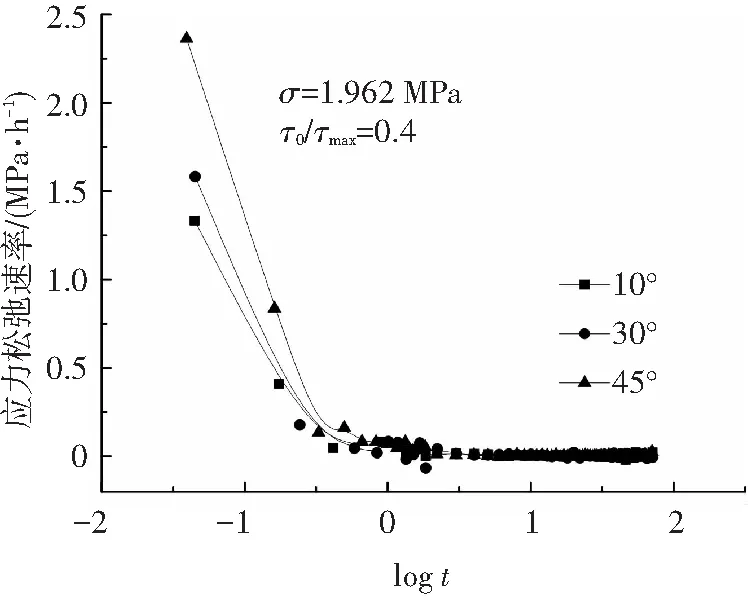
图4 应力松弛速率

文献[1]也指出，岩石在外部荷载作用下将发生蠕变，如果保持试件的应变不变，将发生荷载松弛，一直到作用力与岩石的内应力相互平衡为止，这一个荷载称为“稳定应力”.由于岩石是复杂的非均匀体，在不同剪应力水平下，试件保持恒定应变水平进行松弛，试件的内部结构和变形发生变化(岩石内部微裂隙的延伸和扩展，使加载时产生弹性变形逐渐转化为粘塑性变形)，应力进行调整和转移(裂隙和粘塑性变形缓解岩石介质内的应力集中，内部应力不断降低，产生松弛)，因此，应力松弛过程就是岩石内部应力不断调整和转移的过程，直到内部应力与外部作用力达到平衡.

3 应力松弛方程及参数拟合分析

流变力学中的元件组合模型，因结构简单直观，参数物理意义明确，在工程界被广泛应用.而且流变力学模型被用于揭示安全事故或灾害的流变发展规律[21].但大多数模型没有考虑参数的非线性，即与时间的相关性.现实中，模型参数大小，随应力水平、应力应变状态和应力持续作用时间呈非线性变化.因此，要精确地描述岩石松弛特性，需要考虑岩石力学参数的时间效应.

3.1 Maxwell非线性流变模型

Maxwell模型由一个弹性元件和一个粘性元件串联而成，见图5.该模型的松弛方程为

(1)

式中τ0为初始应力，式(1)表明，当保持ε不变时，应力τ将随时间增长而逐渐减小，并趋近于零，与图3所示的应力曲线基本趋于一个稳定值不太相符.文献[2]在蠕变试验分析时把粘性系数η假定为加载应力和时间的函数.本次松弛试验是应力加载到一定值后不再对试件继续施加作用力，与蠕变实验不同，因此不考虑应力对粘性系数η的影响，只假定粘性系数η是时间t的函数，并且符合线函数关系，即

(2)

式中：A表示试件在加载瞬时(t=0)的初始粘滞系数值，B表示粘滞系数的变化速率，A、B均为常数，根据元件组合模型的串联法则，得到其本构方程：

(3)

根据松弛初始条件：在t=0时，材料发生恒定应变ε0，求解方程可得非线性Maxwell模型的松弛方程：

(4)

式中：τ0为松弛开始时的初始剪应力，G为剪切模量，A、B为拟合得到的参数.

图5 Maxwell模型

根据式(4)，利用Matlab数值计算软件，采用最小二乘法，对法向应力为5.886 MPa时45°结构面的应力松弛曲线进行拟合，拟合结果见图6，图中数字表示剪应力水平，即初始剪应力τ0与抗剪强度τmax的比值，拟合参数见表1.

表1 曲线拟合参数

图6 45°结构面拟合曲线

由图6和表1可知，采用本文提出的松弛方程，对松弛曲线进行拟合时，得到的相关系数较高，说明曲线之间的吻合程度比较高，且试验曲线与拟合曲线的形态、走势基本相同，说明采用非线性Maxwell模型松弛方程能够反映结构面剪切应力松弛特性.

3.2 松弛参数与剪应力水平

粘滞性又称内摩擦，是物体内部质点发生相对位移时，在接触面产生阻碍质点移动的摩擦力.应力松弛过程中，试样内部结构随时间发生变化，质点移动产生的内摩擦力大小也随时间而变化.参数A反映初始粘性系数η的大小，与剪应力水平的关系见图7.从图中可以看出，法向应力σ和初始剪应力τ越大，初始粘性系数η越大.法向应力越大，质点相互移动时需要克服的内摩擦力就大，初始粘性系数也越大.不同应力水平下初始粘性系数不同，反映了非线性松弛属性，而粘性系数随着加载持续时间t的推移而增大，说明弹性越显著，越接近固体，在松弛试验曲线上反映为其流动度逐渐下降，应力松弛量减小，因此松弛曲线呈衰减型.

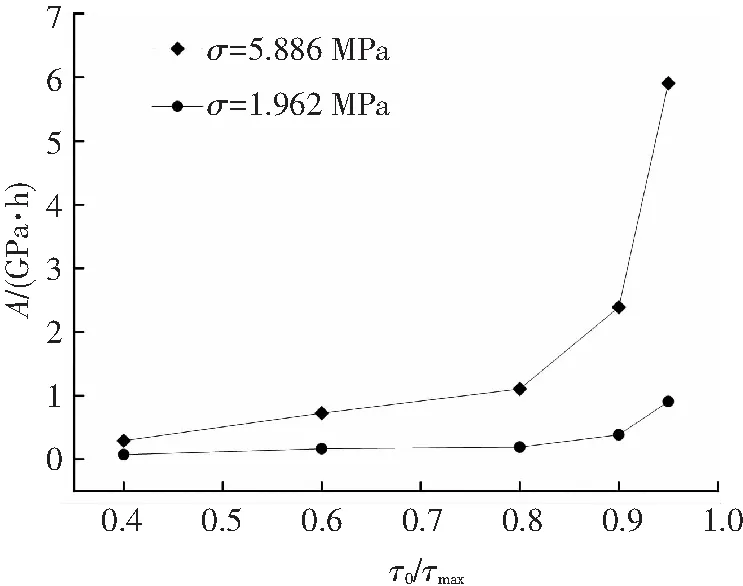
图7 参数A与剪应力水平的关系

4 结构面长期强度的确定

蠕变是在恒定应力作用下，变形随时间缓慢的增加，松弛是在恒定应变作用下，应力随时间逐渐的减小.由于边界条件不同，岩体受应变约束时产生应力松弛，部分荷载转移到内部其它质点而引起蠕变，蠕变的发展进一步促进了松弛的产生.而且现有松弛理论大多基于蠕变理论，在某种程度上也可以认为松弛是蠕变的另一种表现形式，文献[1]更是提到蠕变试验和松弛试验本质上是等价的.因此，本文基于过渡蠕变法确定长期强度的机理，提出通过松弛试验确定岩石长期强度的方法.

4.1 过渡蠕变法确定长期强度

长期强度为岩石能保持长期稳定所能够承受的最大荷载，通常根据蠕变试验采用间接方法确定岩石长期强度，过渡蠕变法是众多方法中比较直接、简单的一种.

文献[1]中指出，稳态蠕变速度为零时的最大荷载值即为岩石的长期强度.换句话说，就是岩石不发生稳态蠕变时的最大载荷值即为岩石的长期强度，不发生稳态蠕变即是只出现衰减蠕变.根据典型蠕变曲线特征可知，稳态蠕变段内卸载，除瞬时恢复和随时间恢复的变形外，还有部分变形残留在材料内成为永久变形；而在衰减蠕变段卸载，材料的弹性变形一部分瞬时恢复，另一部分则随时间增加而恢复.因此，过渡蠕变法可以理解成：只产生粘弹性变形所对应的最大荷载，或者也可以说成是不产生不可恢复的塑性变形所对应最大应力.

4.2 松弛试验确定长期强度的方法

为更好的研究分析结构面的应力松弛性能，定义结构面t时刻的松弛应力τ(t)=τ0-τf(t)，τ0为初始剪应力，τf(t)为经过时间t后的剩余剪应力，Δτ=τ0-τf为松弛应力，即初始剪应力与剩余剪应力的差值.由于结构面的抗剪强度不同，施加的初始剪应力也不相同，为便于对比分析，横轴采用初始应力与抗剪强度的比值，即τ0/τmax比值.不同角度结构面的松弛应力Δτ与剪应力水平的关系见图8.

图8 松弛应力与剪应力水平曲线

由图8可以看出，相同剪应力水平下，爬坡角和法向应力越大，结构面松弛应力也越大；对于相同爬坡角的结构面，法向应力越大，松弛应力越大，而且剪应力水平越大，松弛应力也越大，但松弛应力并不随着应力水平的增大一直增大，而是存在一个峰值.法向应力为1.962 MPa时，10°和30°爬坡角结构面在剪应力水平τ0/τmax=0.9、45°爬坡角结构面在τ0/τmax=0.8时松弛应力达到最大；法向应力为5.886 MPa时，所有爬坡角结构面都在τ0/τmax=0.8时松弛应力达到最大，之后松弛应力逐渐减小.法向应力和爬坡角较小时，松弛应力在应力水平为0.9时达到峰值，法向应力和爬坡角较大时，在应力水平为0.8时达到峰值.

松弛试验时，应变恒定，应力逐渐减小.由弹性应力、应变关系公式σ=Eε可知，弹性模量不变，应力减小，说明弹性变形减少，减少的弹性变形转化为塑性变形，松弛应力的大小取决于弹性变形转化为塑性变形的多少.

根据过渡蠕变法确定长期强度的机理可知，应力小于长期强度，只产生弹性和粘弹性变形；应力大于长期强度，产生不可恢复的塑性变形.因此松弛试验可以认为，当初始剪应力τ0小于长期强度τ∞时，应力与弹性变形成正比，应力越大产生的弹性变形越大，转化为塑性变形的弹性变形量也随之增多，松弛应力越大；初始剪应力τ0大于长期强度τ∞时，变形成分发生变化，此时变形由弹性变形和塑性变形组成，塑性变形的产生导致弹性变形减少，转化为塑性变形的弹性变形量减少，松弛应力也随之减小.这也是图8中松弛应力不随应力水平的提高一直增大，而出现峰值的原因.

基于以上分析，提出分级加载松弛试验确定岩石长期强度的方法，即出现松弛应力峰值的剪应力为长期强度，其确定长期强度的机理与过渡蠕变法可以取得一致.根据本文提出的确定长期强度方法，法向力和结构面爬坡角较小时，长期强度τ∞与抗剪强度τmax比值约为0.9，法向力和结构面爬坡角较大时，长期强度τ∞与抗剪强度τmax比值约为0.8.在低法向力作用下，结构面的长期强度主要表现在结构面的摩擦，随着爬坡角的增大摩擦强度转为切齿强度，而摩擦的长期强度与瞬时强度的差值较小，切齿强度差值较大；在较大的法向力作用下，爬坡角的摩擦机理基本消失，而长期强度所反映的都是切齿强度，爬坡角的影响被削弱.因此，出于安全考虑可取τ∞/τmax=0.8时的剪应力作为结构面的长期强度.这与文献[22]用相同的加载方式，对30°和45°爬坡角规则齿形结构面进行蠕变试验，采用等时曲线法确定长期强度为抗剪强度的80%，基本相同.由于一般情况下，采用分级加载法很难直接得到松弛应力峰值对应的剪应力，只能通过一个荷载区间来确定长期强度.试验时分级越多，相邻两级荷载值相差越小，则长期强度范围越小，值越准确.

5 结 论

1) 规则齿形结构面的剪切松弛规律符合一般材料的实际应力松弛特性，松弛效应明显，松弛曲线为衰减型曲线，基本上可以分为瞬时松弛、减速松弛、稳态松弛3个阶段，没有出现松弛破坏阶段.

2) 根据流变参数的非线性，提出了非线性Maxwell模型的松弛方程，对45°结构面的松弛曲线进行拟合，拟合曲线和试验曲线之间的吻合程度较高，基本上可以描述剪切松弛过程.

3) 规则齿形结构面松弛应力与剪应力水平曲线表明，相同剪应力水平下，爬坡角和法向应力越大，结构面松弛应力也越大；对于相同爬坡角结构面，法向应力越大，松弛应力也越大，而且剪应力水平越高，松弛应力越大，但松弛应力并不随着应力水平的增大一直增大，而是存在一个峰值.

4)在讨论试件松弛特性的基础上，提出了分级加载松弛试验确定长期强度的方法，即：松弛应力峰值对应的剪应力为岩石的长期强度.

[1] 刘雄.岩石流变学概论[M].北京:地质出版社,1994. LIU Xiong. Introduction to rock rheology[M]. Beijing: Geology Publishing House, 1994.

[2] 孙钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999. SUN Jun. The rheology and engineering application of the geotechnical material[M]. Beijing: China Architecture and Building Press,1999.

[3] 谢和平,陈忠辉. 岩石力学[M].北京:科学出版社,2004. XIE Heping, CHEN Zhonghui. Rock mechanics[M]. Beijing: Science Press, 2004.

[4] LADANYI B, JOHNSTON G H. Behavior of circular footings and plate anchors embedded in permafrost[J]. Canadian Geotechnical Journal, 1974, 11:531-553.

[5] 邱贤德,庄乾城. 岩盐流变特性的研究[J]. 重庆大学学报(自然科学版),1995，18(4):96-103. QIU Xiande, ZHUANG Qiancheng. Research on the rheology behaviour of rock salt[J]. Journal of Chongqing University: Natural Science, 1995, 18(4):96-103.

[6] YANG C, DAEMEN J J K, YIN J H. Experimental investigation of creep behavior of salt rock[J]. International Journal of Rock Mechanics & Mining Sciences, 1999, 36(2):233-242.

[7] 杨春和,殷建华. 盐岩应力松弛效应的研究[J]. 岩石力学与工程学报,1999，18(3):262-265. YANG Chunhe, YIN Jianhua. The investigation of stress relaxation of salt rock[J]. Chinese Journal of Rock Mechanics and Engineering, 1999,18(3): 262-265.

[8] 杨春和,白世伟,吴益民. 应力水平及加载路径对盐岩时效的影响[J]. 岩石力学与工程学报,2000，19(3):270-275. YANG Chunhe, BAI Shiwei, WU Yimin. Stress level and loading path effect on time dependent properties of salt rock[J]. Chinese Journal of Rook Mechanics and Engineering, 2000, 19(3): 270-275.

[9] 冯涛, 王文星, 潘长良. 岩石应力松弛试验及两类岩爆研究[J]. 湘潭矿业学院学报, 2000, 15(1): 27-31. FENG Tao, WANGWenxing, PAN Changliang. Stress relaxation tests of rock and research on two types of rockburst[J]. Journal of Xiangtan Mining Institute, 2000, 15(1): 27-31.

[10]唐礼忠, 潘长良, 谢学斌. 深埋硬岩矿床岩爆控制研究[J]. 岩石力学与工程学报, 2003, 22(7): 1067-1071. TANG Lizhong, PAN Changliang, XIE Xuebin. Study on rockburst control in deep-seated hard ore deposit[J]. Chinese Journal of Rock Mechanics and Engineering, 2003,22(7): 1067-1 071.

[11]唐礼忠, 潘长良. 岩石在峰值荷载变形条件下的松弛试验研究[J]. 岩土力学, 2003, 24(6): 940-942. TANG Lizhong,PAN Changliang. Experiment study on properties of stress relaxation of rock under deformation at peak load[J]. Rock and Soil Mechanics，2003，24(6)：940-942.

[12]于怀昌,周敏,刘汉东,等. 粉砂质泥岩三轴压缩应力松弛特性试验研究[J]. 岩石力学与工程学报,2011，30(4):803-811. YU Huaichang，ZHOU Min，LIU Handong，et al. Experimental investigation on stress relaxation properties of silty mudstone under triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering，2011，30(4)：803-811.

[13]曹平,郑欣平,李娜,等. 深部斜长角闪岩流变试验及模型研究[J]. 岩石力学与工程学报,2012，31(增1):3015-3021. CAO Ping，ZHENG Xinping，LI Na，et al. Experiment and model study of rheological characteristics for deep amphibolite[J]. Chinese Journal of Rock Mechanics and Engineering，2012，31(S1)：3015-3021.

[14]于怀昌,李亚丽,刘汉东. 粉砂质泥岩常规力学、蠕变以及应力松弛特性的对比研究[J]. 岩石力学与工程学报,2012,31(1):60-70. YU Huaichang, LI Yali, LIU Handong. Comparative study of conventional mechanical, creep and stress relaxation properties of silty mudstone under triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 60-70.

[15]于怀昌,李亚丽,刘汉东. 粉砂质泥岩三轴压缩应力松弛本构模型研究[J]煤炭学报,2011，36(8):1258-1263. YU Huaichang，LI Yali，LIU Handong. Study of stress relaxation model of silty mudstone under triaxial compression[J]. Journal of China Coal Society，2011，36(8)：1258-1263.

[16]田洪铭,陈卫忠,赵武胜,等. 宜-巴高速公路泥质红砂岩三轴应力松弛特性研究[J]. 岩土力学,2013,34(4):981-986 TIAN Hongming，CHEN Weizhong，ZHAO Wusheng，et al. Analysis of triaxial stress relaxation properties of redsilty mudstone of yichang badong highway[J]. Rock and Soil Mechanics，2013，34(4)：981-986.

[17] 于怀昌,邹明俊,刘汉东,等. 岩石非定常黏弹性应力松弛本构模型研究[J]. 四川大学学报(工程科学版),2015，47(增2):54-60. YU Huaichang，ZOU Mingjun，LIU Handong，et al. Study of non-stationary viscoelastic stress relaxation model of rock[J]. Journal of Sichuan University (Engineering Science Edition)，2015, 47 (S2): 54-60.

[18]刘昂,沈明荣,蒋景彩,等. 基于应力松弛试验的结构面长期强度确定方法[J]. 岩石力学与工程学报,2014，33(9):1916-1924. LIU Ang, SHEN Mingrong, JIANG Jingcai，et al. Determining long-term strength of rock with discontinuity using shear stress relaxation test[J]. Chinese Journal of Rock Mechanics and Engineering, 2014，33(8):1916-1924.

[19]周文锋,沈明荣. 规则齿型结构面的应力松弛特性试验研究[J]. 土工基础,2014，28(2):138-141. ZHOU Wenfeng SHEN Mingrong. Experimental study of stress relaxation characteristics of regular rock mass discontinuties[J].Soil Eng.And Foundation,2014, 28(2):138-141 [20]李永盛. 单轴压缩条件下四种岩石的蠕变和松弛试验研究[J]. 岩石力学与工程学报,1995，14(1):39-47. LI Yongsheng. Creep and relaxation of 4 kinds of rock under uniaxial compression tests[J]. Chinese Journal of Rock Mechanics and Engineering，1995，14(1)：39-47.

[21]张守健.建筑施工安全事故流变过程[J]．哈尔滨工业大学学报，2011,43(2):89-91． ZHANG Shoujian. Research on the rheological process of construction safety accidents[J]．Journal of harbin institute of technology，2011,43(2):89-91． [22]侯宏江,沈明荣. 岩体结构面流变特性及长期强度的试验研究[J]. 岩土工程技术,2003(6):324-326,353. HOU Hongjiang，SHEN Mingrong. Rheological properties of rock mass discontinuities and trial research of its long-term strength[J]. Geotechnical Engineering Technique，2003(6)：324-326，353.

(编辑 赵丽莹)

Shear relaxation characteristic of serrate structure surface under stepwise loading

TIAN Guanghui1, SHEN Mingrong1,2, ZHOU Wenfeng1, LI Yanlong3, LIU Zhikui4

(1.College of Civil Engineer, Tongji University, Shanghai 200092, China; 2.Key Laboratory of Geotechnical and Underground Engineering (Tongji University), Ministry of Education, Shanghai 200092, China; 3. Pingdiingshan Highway Administration,Pingdiingshan 467000, Henan, China; 4. College of Civil Engineering and Architecture, Guilin University of Technology,Guilin 541004, Guangxi, China)

To investigate the relaxation characteristic of rock mass discontinuity with different slope ratios and normal stresses, the stress relaxation tests of dentate discontinuity poured by cement mortar on the condition of shear stress were carried out by using biaxial creep machine. The test results show that: the relaxation curves can be divided into three stages, i.e. the instantaneous relaxation stage, attenuation relaxation stage and stable relaxation stage; the shear nonlinear Maxwell relaxation equation is obtained by constructing the relation between viscosity coefficient and time, the curves of the empirical equation agree with the test ones and get change law of initial viscosity coefficient and change rate with shear stress; according to change law of relaxation stress with shear stress and mechanism of determining long-term strength using transition creep law, a stress relaxation method is proposed to determine the long-term strength, which is relaxation stress peak method.

rock mass discontinuity; shear stress; stress relaxation; nonlinear Maxwell relaxation equation; long-term strength

10.11918/j.issn.0367-6234.2016.12.015

2015-09-28

国家自然科学基金(41072203,51169004); 广西岩土力学与工程重点实验室基金(12-A-01-01)

田光辉(1982—)，男，博士研究生; 沈明荣(1952—)，男，教授，博士生导师

沈明荣，shenmingrong@tongji.edu.cn

TU45

A

0367-6234(2016)12-0108-06