微波频段粗糙金属表面等效电导率的数值计算及验证

王怡然,叶鸣,高凡,陈雄,贺永宁

(西安交通大学电子与信息工程学院,710049,西安)



微波频段粗糙金属表面等效电导率的数值计算及验证

王怡然,叶鸣,高凡,陈雄,贺永宁

(西安交通大学电子与信息工程学院,710049,西安)

为了评估表面粗糙度对微波频段金属表面等效电导率的影响,提出了一种基于梯度模型的粗糙金属表面等效电导率数值计算方法并进行实验验证。首先基于电导率梯度模型,将粗糙金属表面等效为电导率渐变的若干光滑薄层的叠加;其次基于电磁波在薄层内的损耗及薄层间界面的传输特性,对粗糙金属表面的总损耗进行数值计算并获取等效表面电导率;最后运用替换端板谐振腔法对不同粗糙度的黄铜样片在8.98、10.78 GHz进行表面电导率测试。实验结果表明:在0.1～3 μm的均方根粗糙度范围内,等效电导率随粗糙度增加而减小,且基于梯度模型的等效电导率计算方法所得理论预测值相比于已有理论更符合实测结果。

微波频段;均方根粗糙度;谐振腔

随着无线通信的快速发展,不论是腔体微波器件,还是高频电路板,金属表面粗糙度引起的微波损耗均是设计阶段应该考虑的重要因素。微波频段下,由于趋肤效应,电流在金属表面几微米的深度内流动。因此,表面微观粗糙度的增加势必导致电流路径变长,从而引起微波损耗增加。随着通信系统不断朝着高频发展,粗糙表面引起的衰减显著增加,粗糙表面电导率问题日益受到关注。

国内外学者对粗糙表面在微波频段的损耗问题的研究由来已久[1-5]。从理论研究角度来看,已有的分析方法可分为2类:第一类是基于实验数据拟合的唯象模型[6-7];第二类是基于解析推导或数值计算的物理模型[8-12]。第一类方法的优点是给出了形式简洁的等效电导率表达式,可方便地应用于全波仿真算法,其缺点是模型定量计算结果准确度不高。第二类方法又可以分为2种:基于周期性规则微结构表面的模型[8-9]以及基于随机粗糙表面的模型[10-12]。这类方法的优点是具有较为清楚的物理图像,缺点是计算方法复杂、需要结合复杂的电磁理论进行分析及计算。文献[11-12]针对微波平面电路的损耗问题提出了粗糙表面电导率的梯度模型,并计算了毫米波频段的微带线损耗,得到了满意的结果。

本文基于文献[12]中提出的粗糙表面电导率梯度模型,考虑不同介质层间平面波的透射系数,建立了均方根粗糙度影响表面电导率的分层模型及其计算方法。利用替换端板谐振腔法对具有不同粗糙度的黄铜平板样片表面电导率进行了测试,并将测试结果分别与文献中模型及本文模型得到的理论计算结果进行了对比。

1 分层模型及其计算方法

为了描述粗糙表面对微波平面电路导体损耗特性的影响,Gold等人提出了粗糙表面电导率的梯度模型[12],其主要思想是:当电磁波不断渗入粗糙表面时,所“穿过的”导体越来越多,因而所呈现出的导电性也越来越接近材料的体电导率。这一电导率的渐变过程,与粗糙表面累积概率密度函数的变化趋势一致,由此提出了如下的电导率梯度模型(假设粗糙表面服从高斯分布)

σ(x)=σbulkDCDF(x)

(1)

式中:σ(x)为距离表面深度为x处的电导率;σbulk为体电导率;DCDF(x)为粗糙表面的累积概率密度函数。以高斯分布粗糙表面为例,当均方根粗糙度为Rq时,相应的累积概率密度函数为

(2)

式中:e(x)为误差函数。由此可见,如果将粗糙表面等效为光滑表面,其电导率将由外向内不断增加。当渗入表面深度达到一定值时,其电导率即为材料的体电导率。

为了计算微波频段粗糙表面的等效电导率,可依据梯度模型将具有粗糙表面的导体材料等效为由若干光滑薄层叠加而构成。在电导率分层模型中,每个薄层的厚度是相等的,从物理意义来讲,当薄层厚度设置得较薄时,能够较好地反映电导率的渐变特性,电导率分层模型可以得出较为准确且稳定的结果;然而,从数学意义来讲,当薄层厚度较薄时,计算量会显著增加。基于这两方面的考虑,本文中的薄层厚度设定为趋肤深度的1/100。

在每一薄层内,假设电导率为恒定值(依据该层深度及梯度模型确定具体值),通过计算每个薄层内的导体损耗并求和可以得到总损耗。以第k层为例进行说明,该层的厚度范围是(xk-1,xk),第k层的电导率取值为该层中间位置的电导率值,即

(3)

依据电磁理论,电磁波在不同介质间传播时,将在分界面上发生反射和透射[6]。对于分层模型,电磁波在朝向导体内部渗入的过程中,一方面在每个分界面处存在一定的透射系数,另一方面电磁波在每层介质内会经历一定的衰减。综合考虑这些因素后,得到第k层导体中单位面积的焦耳损耗为

[-2αk(k-1)Δx]·

(4)

式中:E0为电场幅度;αk=(πfμσk)1/2;Δx为薄层厚度;Tm为第m层的透射系数

(5)

本征阻抗为

(6)

2 实验及结果分析

2.1 实验方法

替换端板谐振腔法测量表面电导率的基本原理[13-14]是:使用同一材料制作一个上端板可拆卸的圆柱谐振腔(工作于TE011模式),测量其Q值为Q0,然后用待测平板替换上端板,测得此时的Q值为Q1,根据这2个测试值即可算出待测平板与原盖板材料的表面电阻之比,如果原盖板材料的表面电阻为已知,则可求解出待测平板的表面电阻绝对值。

依据电磁场相关理论[13-14]可知

(7)

式中:f为谐振频率;Est为谐振腔存储的能量;Lsw0为圆柱腔体内部侧壁上的导体损耗;Lew0是腔体上下端板上的导体损耗。当上端板被其他材料的表面电阻待测盖板所替换时,式(7)变为

(8)

定义腔体形状决定的几何因子K为

(9)

由于任一壁上的损耗对于表面电阻来说是成比例分配的,因此令原始谐振腔的无载Q值与上端板被替换了的待测谐振腔的无载Q值相比并化简得到待测样表面电阻为

(10)

图1 上盖板可拆卸的圆柱谐振腔实物图

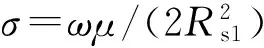
采用机械加工的方法制备了不同粗糙度的黄铜样片(样片面积为50 mm×50 mm,厚度为5 mm)。采用激光扫描显微镜(VK-9700)对样片表面5个位置(十字排布)进行采样,测量其表面粗糙度,采样面积为3.5×105μm2,X、Y方向上2个像素点的间距为689 nm,其中X方向上像素点为1 024个,Y方向上像素点为768个,Z方向上2个像素点的间距为1 nm。由激光扫描微镜观测到的样片表面二维形貌图如图2所示,可以看到其表面有交错不一的沟壑与凸起。腔体Q值测量采用Agilent E8363B型号网络分析仪,每个样片连续测量4次、每次顺时针方向旋转90°,以4次测量的均值作为该样片测试值。

图2 不同粗糙度样片的二维形貌图

2.2 实验结果及分析

激光扫描显微镜(VK-9700)的测试结果显示,黄铜样片的面粗糙度范围为0.30～1.64 μm。图3是经表面形貌测试后得到的各采样点高度分布数据,从中可以看出粗糙表面高度近似服从高斯分布。

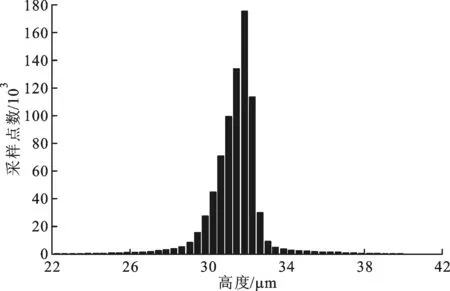
图3 样片表面高度分布直方图

图4和图5分别给出了8.98、10.78 GHz频点处测得的不同粗糙度表面电导率结果(为方便与理论计算对比,结果表示为相对于粗糙度为0.3 μm样片的归一化电导率,所测样片的最小粗糙度为0.3 μm)。作为对比,图中还给出了有关模型及本文模型的计算结果。其中,H模型为文献[6]中给出的Hammerstad模型

(11)

式中:σeff为等效电导率;σ0为理想电导率;δs为趋肤深度;h为均方根粗糙度。T模型为文献[11]中给出的模型

σeff=

(12)

(13)

H模型、T模型、G模型得到的是样品表面的线粗糙度与等效电导率的直接关系,本文实验测量的是面粗糙度与等效电导率之间的关系,面粗糙度在实际应用中比线粗糙度的可控性更高,且更为实用。作为解决实际工程问题的经验模型,这3个模型适用的粗糙度等参数范围是有限的,而本文特殊设计的粗糙度在一定程度上超过了经典模型的适用范围。

图4 铜样片表面电阻测试结果及4种模型的 计算结果(8.98 GHz)

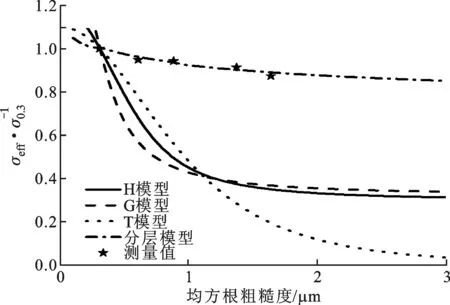
图5 铜样片表面电阻测试结果及4种模型的 计算结果(10.78 GHz)

由图4和图5给出的测试结果可以看到,当均方根粗糙度从0.3 μm增加至1.6 μm时,等效电导率呈下降趋势,在8.98和10.78 GHz处的理论预测等效电导率与实际测量值的最大误差分别为4.79%和2.4%。与文献中给出的粗糙表面等效电导率模型相比,分层模型得到的理论计算结果与实际测量更为贴近,从而证实了其合理性。

3 结 论

依据粗糙表面梯度模型,考虑分层介质的透射系数,建立了粗糙表面等效电导率的分层模型及其计算方法。采用替换端板谐振腔法测量了具有不同粗糙度的黄铜样片,结果表明:粗糙度增加导致等效电导率减小;在一定粗糙度范围内,利用分层模型得到的理论计算结果与实际测量值最大误差为4.79%。与文献中已有的模型相比,分层模型得到的理论结果与实际测量值更为贴近。

[1] MORGAN S P. Effect of surface roughness on eddy current losses at microwave frequencies [J]. Journal of Applied Physics, 1949, 20(4): 352-362.

[2] EHSAN M A, ZHOU Z, LIU L, et al. An analytical through silicon Via (TSV) surface roughness model applied to a millimeter wave 3-D IC [J]. IEEE Transactions on Electromagnetic Compatibility, 2015, 57(4): 1-12.

[3] YI M, LI S, YU H, et al. Surface roughness modeling of substrate integrated waveguide in D-Band [J]. IEEE Transactions on Microwave Theory & Techniques, 2016, 64(4): 1209-1216.

[4] LO H L, CHEAH B E. Study of conductor surface roughness impact on package insertion loss [C]∥2015 IEEE 17th Electronics Packaging and Technology Conference. Piscataway, NJ, USA: IEEE, 2015: 7412292.

[5] 贾琦, 黄斌科. 粗糙导体表面提取印刷电路板介质参数的微分外推方法 [J]. 西安交通大学学报, 2015, 49(8): 11-16.

JIA Qi, HUANG Binke. A differential extrapolation method to extract dielectric parameters of PCB with roughened conductor surface [J]. Journal of Xi’an Jiaotong University, 2015, 49(8): 11-16.

[6] 波扎尔. 微波工程 [M]. 北京: 电子工业出版社, 2006: 26-29.

[7] GROISS S, BARDI I, BIRO O, et al. Parameters of lossy cavity resonators calculated by the finite element method [J]. IEEE Transactions on Magnetics, 1996, 32(3): 894-897.

[8] HUANG B, CHEN J, JIANG W. Effects of surface roughness on TE modes in rectangular waveguide [J]. Journal of Infrared, Millimeter, and Terahertz Waves, 2009, 30(7): 717-726.

[9] CHEN C D, TZUANG C K C, PENG S T. Full-wave analysis of a lossy rectangular waveguide containing rough inner surfaces [J]. IEEE Microwave and Guided Wave Letters, 1992, 2(5): 180-181.

[10]GOLD G, HELMREICH K. A physical model for skin effect in rough surfaces [C]∥2012 7th European Microwave Integrated Circuit Conference. Piscataway, NJ, USA: IEEE, 2012: 631-634.

[11]GOLD G, HELMREICH K. Surface impedance concept for modeling conductor roughness [C]∥2015 IEEE MTT-S International Microwave Symposium. Piscataway, NJ, USA: IEEE, 2015: 1-4.

[12]TSANG L, GU X, BRAUNISCH H. Effects of random rough surface on absorption by conductors at microwave frequencies [J]. IEEE Microwave and Wireless Components Letters, 2006, 16(4): 221-223.

[13]叶鸣, 贺永宁, 胡少光, 等. 微波频段金属表面电阻的谐振腔测试方法研究 [C]∥2013全国天线年会论文集. 北京: 电子工业出版社, 2013: 1428-1430.

[14]WILKER, C, SHEN Z Y, PANG P, et al. 5 GHz high-temperature-superconductor resonators with highQand low power dependence up to 90 K [J]. IEEE Transactions on Microwave Theory and Techniques, 1991, 39(9): 1462-1467.

[15]曾成. 镜像法测试高温超导薄膜微波表面电阻的研究 [D]. 成都: 电子科技大学, 2009: 42-47.

(编辑 刘杨)

A Numerical Method of Equivalent Electrical Conductivity of Rough Metal Surface at Microwave Frequency Band and Its Verification

WANG Yiran,YE Ming,GAO Fan,CHEN Xiong,HE Yongning

(School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A numerical method of equivalent conductivity based on a gradient model is proposed to evaluate the effect of surface roughness on the equivalent electrical conductivity of metal surface at microwave band and experimental verification of the method is performed. Firstly, it is based on the gradient model of conductivity that the surface of a rough metal is equivalent to the superposition of several smooth thin layers. Secondly, the loss and transmission characteristics of the electromagnetic wave in each thin layer is based to calculate the total loss of the rough metal surface and to obtain the equivalent surface conductivity. Finally, the resonant cavity with replaceable end plate is used to measure the surface conductivities of machined brass samples with various roughness at 8.98 GHz and 10.78 GHz, respectively. Results indicate that, the equivalent conductivity decreases as the roughness increases for samples with RMS roughness in the range of 0.1-3 μm and that the theoretical predicted value of the equivalent conductivity from the proposed numerical method has a better agreement with measurement results than that from existing theories.

microwave frequency band; root mean square roughness; resonant cavity

2016-03-29。 作者简介:王怡然(1990—),男,硕士生;贺永宁(通信作者),女,教授,博士生导师。 基金项目:国家自然科学基金资助项目(615013564)。

时间:2016-07-22

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160722.1953.002.html DOI:10.7652/xjtuxb201610003

TM931

A

0253-987X(2016)10-0015-04