基于虚拟弹性体的快速动网格方法

仲继泽,徐自力,陶磊

(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2.西安交通大学航天航空学院,710049, 西安; 3.国家电网浙江北仑第一发电有限责任公司,315800,浙江宁波)



基于虚拟弹性体的快速动网格方法

仲继泽1,2,徐自力1,2,陶磊3

(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2.西安交通大学航天航空学院,710049, 西安; 3.国家电网浙江北仑第一发电有限责任公司,315800,浙江宁波)

为减少流固耦合的计算时间,在现有弹性体方法的基础上,发展了一种快速动网格方法。首先根据弹性体方法的基本假设,将流场网格所包围的空间区域视为虚拟弹性体,然后将结构与该虚拟弹性体视为一个整体系统,并计算其固有振动的振型及频率,最后以结构受到的流体作用力为激励,通过振型叠加法计算结构网格及流场网格节点的位移。考虑到实际结构的流固耦合振动多为低阶模态的振动,在流固耦合计算中可以通过低阶模态的叠加计算流场网格节点的位移,从而达到快速更新流场网格的目的。采用该快速动网格算法,对某弹性梁颤振问题进行了流固耦合分析,计算结果与已有文献的结果吻合很好,说明了该算法的正确性。与现有的弹性体方法相比,该算法使流固耦合计算时间减少了65.5%。对Wing 445.6模型的颤振问题进行了分析,得到颤振边界与实验值吻合良好,且与现有弹性体法相比,可以减少计算时间54.8%。

流固耦合;弹性体方法;快速动网格方法

在流固耦合计算中,为考虑结构振动对流场的影响,通常需要采用动网格方法更新流场网格[1]。目前所发展的网格变形方法主要有弹簧法[2]、弹性体方法[3]、温度体方法[4]及径向基函数方法[5]。与其他动网格方法相比,弹性体方法是一种基于物理模型的网格变形方法,把流场网格变形作为一个弹性体变形问题进行求解,更能贴近结构弹性变形的物理实际。文献[6]率先提出了弹性体方法,将流场网格所围绕的空间区域视为虚拟弹性体,流场边界变形作为弹性体的位移载荷,通过求解静力平衡方程计算网格节点的位移。

在早期的研究中,文献[6-8]都假定虚拟弹性体的弹性模量是各向同性的,采用这种弹性体方法更新流场网格时,边界层网格容易发生畸变,网格变形能力受到限制。文献[9]引入了刚度系数,将虚拟弹性体刚度与流场网格大小关联,通过增加小网格附近虚拟弹性体的刚度,使得网格变形能力和变形网格的质量得到显著提高。文献[10]提出了分层弹性体方法,采用分层的思想,逐层决定虚拟弹性体的刚度,提高了网格变形能力。但是,在流固耦合计算中,每一时间步,都需要更新流场网格,且流场网格的数量通常为100万甚至是1 000万,因此流场网格变形的静力平衡方程规模大,反复求解会占用大量的计算时间。

本文在弹性体方法的基础上,发展了一种快速动网格方法。将流场网格所包围的空间区域视为虚拟弹性体,推导了结构与虚拟弹性体同步振动的动力学方程。在流固耦合计算的每一时间步,通过低阶模态的叠加,计算流场网格变形的节点位移,并更新流场网格。采用本文的动网格算法,对弹性梁颤振算例进行了流固耦合计算,计算结果与已有文献的结果吻合很好,说明了本文算法的正确性。

1 快速动网格方法

结构的网格节点可以分成流固耦合面节点和非流固耦合面节点两个部分,据此将结构的振动控制方程写成分块矩阵的形式

(1)

式中:Ms、Cs、Ks分别是结构的质量矩阵、阻尼矩阵和刚度矩阵;Xs_in、Xs_n_in分别是结构流固耦合面节点位移和非流固耦合面节点位移;Fin是结构流固耦合面受到的流体作用力。

结构振动会改变流场的边界,需要采用动网格方法对流场网格节点坐标进行更新。在弹性体方法中,流场网格所围绕的空间区域被视为虚拟弹性体,首先设定虚拟弹性体的弹性模量Ep,然后采用有限元方法计算得到的整体刚度矩阵Kp。在虚拟弹性体变形时,流场网格节点位移Xp满足静力平衡方程[10]

(2)

式中:Xp_in、Xp_n_in分别是流场网格流固耦合面节点位移和非流固耦合面节点位移。对结构的网格流固耦合面节点的位移Xs_in进行插值,可以计算出流场网格流固耦合面节点的位移

Xp_in=NXs_in

(3)

式中:N是插值系数矩阵。流场网格变形的静力平衡方程可以改写为

(4)

将结构与流场网格域的虚拟弹性体视为一个整体系统,通过叠加结构振动控制方程和虚拟弹性体的静力平衡方程,得到该整体系统的振动方程

(5)

将该动力学系统的固有频率和正则振型分别记为ω和Ψ。式(5)经坐标变换后,得到正则坐标ξ下的动力学方程

(6)

式中:ζ是阻尼比;Q是正则坐标下的流体作用力。

(7)

(8)

(9)

将式(6)写成分量的形式如下

(10)

模态位移可以采用Wilson-θ方法[11]计算得到。实际结构的流固耦合振动多与低阶模态相关[12],因此通过低阶模态的叠加可以快速计算出结构及流场网格节点的位移

(11)

式中:n是参与流固耦合振动的模态的数量。

将固有频率矩阵写成分块矩阵的形式

(12)

式中:ωs是结构振动主导的模态的固有频率;ωp是虚拟弹性体振动主导的模态的固有频率。

固有模态是指振动系统自由振动时的固有频率及振型。本文将结构与流场网格域的虚拟弹性体作为一个整体系统。在整体系统的固有模态中,如果结构部分基本保持了自身的固有模态,将整体系统的固有模态称为结构振动主导的模态。将振型矩阵写成分块矩阵的形式

(13)

式中:Ψss是整体系统振型对应的结构部分的振型;Ψpp是整体系统振型对应的虚拟弹性体部分的振型。

根据固有频率与刚度矩阵之间的关系式(8),结构振动主导的模态的固有频率可以采用下式表达

(14)

将结构部分的振动Ψss代入到结构的振动控制方程式(1)中,可以得到结构固有频率的表达式为

(15)

与结构的刚度相比,虚拟弹性体的刚度必须是小量。即,虚拟弹性体的弹性模量必须满足下式

(16)

式中:Es为结构的弹性模量。

2 算例验证

采用文献[13]的弹性梁颤振算例验证本文提出的动网格高效算法。流场及弹性梁的具体尺寸见图1。梁的密度为1.0×104kg/m3,弹性模量为1.4×106Pa,泊松比为0.4。流体的密度为1 000 kg/m3,动力学黏度为1 Pa·s。流场的左端面为流场的入口,采用速度进口边界条件,流速方向与进口端面垂直,大小沿y方向呈抛物线分布

(17)

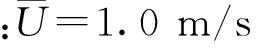
流场的右端面为流场的出口,采用压力出口边界,设定出口的平均静压值为0。流场的上端面和下端面、弹性梁的流固耦合面及左端的圆形壁面均采用无滑移边界。

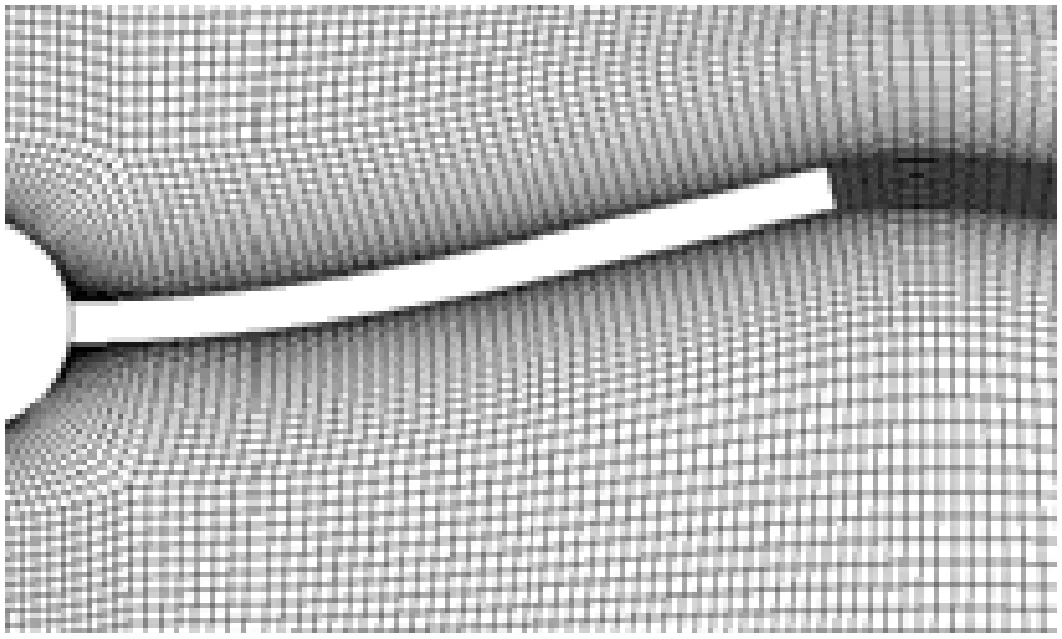
图1 弹性梁及附近流场区域

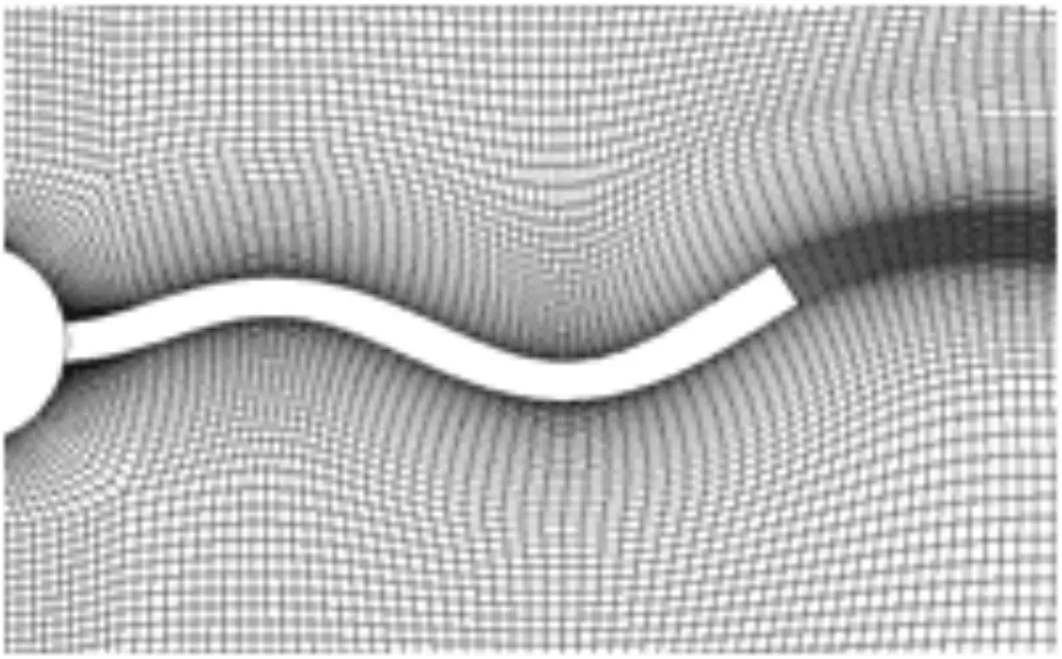
流场及弹性梁的网格见图2。梁的网格共有4节点矩形单元153个,节点208个;流场共有4节点矩形单元19 627个,节点20 034个。

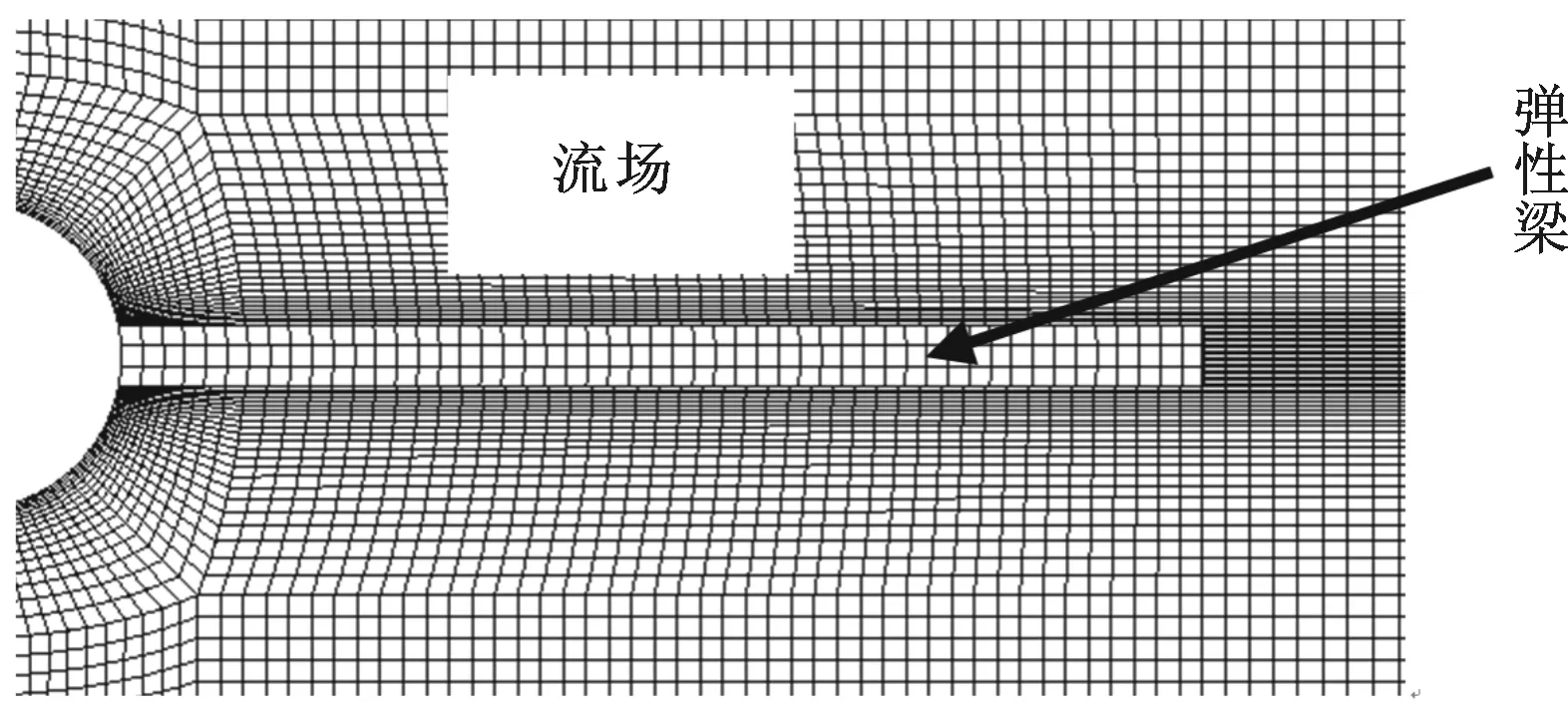
图2 弹性梁及流场网格

2.1 流场网格域虚拟弹性体的弹性模量

本文将虚拟弹性体和结构作为一个整体系统进行研究,结构的固有振动特性势必受到虚拟弹性体的影响。为了保证计算结果的正确性,必须使结构基本上保持原有的固有振动特性。如果设置的虚拟弹性体弹性模量不恰当,会使弹性梁振动主导的模态频率及振型偏离其固有振动频率和振型,从而产生错误的计算结果,因此必须对流场网格设定合适的弹性模量。本文以弹性模量比对数为参数,分析虚拟弹性体对弹性梁振动主导的模态频率及振型的影响,以确定虚拟弹性体的弹性模量。弹性模量比对数定义如下

R=lg(Es/Ep)

(18)

频率偏差定义如下

(19)

式中:fs-p是弹性梁振动主导的模态的固有频率;fs是弹性梁的固有频率。

频率偏差与弹性模量比对数的关系见图3。从图中可以看出:在虚拟弹性体的弹性模量一定的情况下,随着模态阶数的增加,频率偏差会下降;随着弹性模量比对数的增加,频率偏差逐渐减小;当弹性模量比对数大于等于6,虚拟弹性体对弹性梁振动主导的模态频率的影响基本上可以忽略。

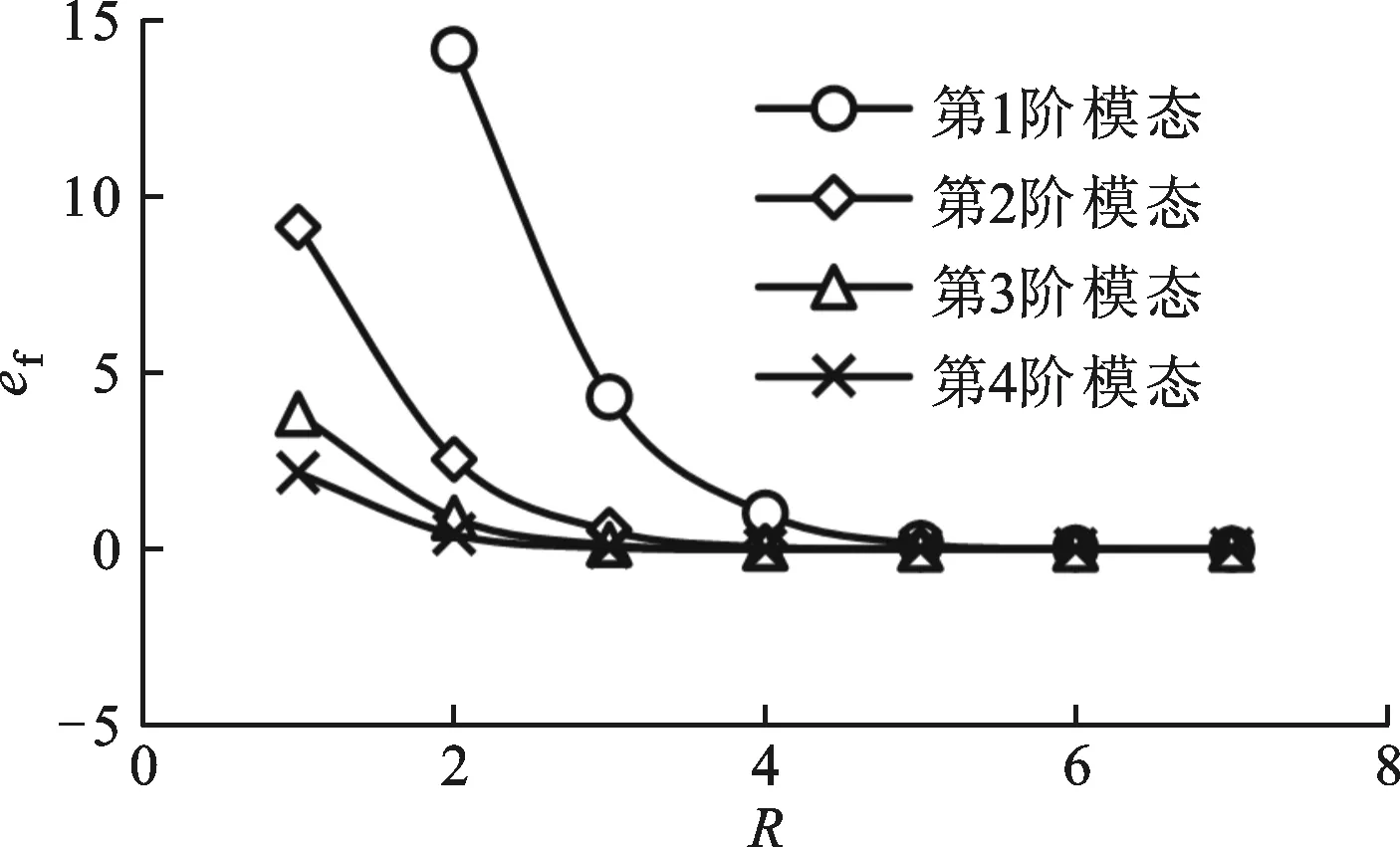
图3 频率偏差与弹性模量比对数的关系

弹性模量比对数与弹性梁振动主导的模态振型之间的关系见图4,其中位移和弹性梁长度均为无量纲量。随着弹性模量比对数的增大,虚拟弹性体对弹性梁振型的影响逐渐减小。当弹性模量比对数大于等于5,虚拟弹性体对弹性梁振动主导的模态振型的影响基本上可以忽略。

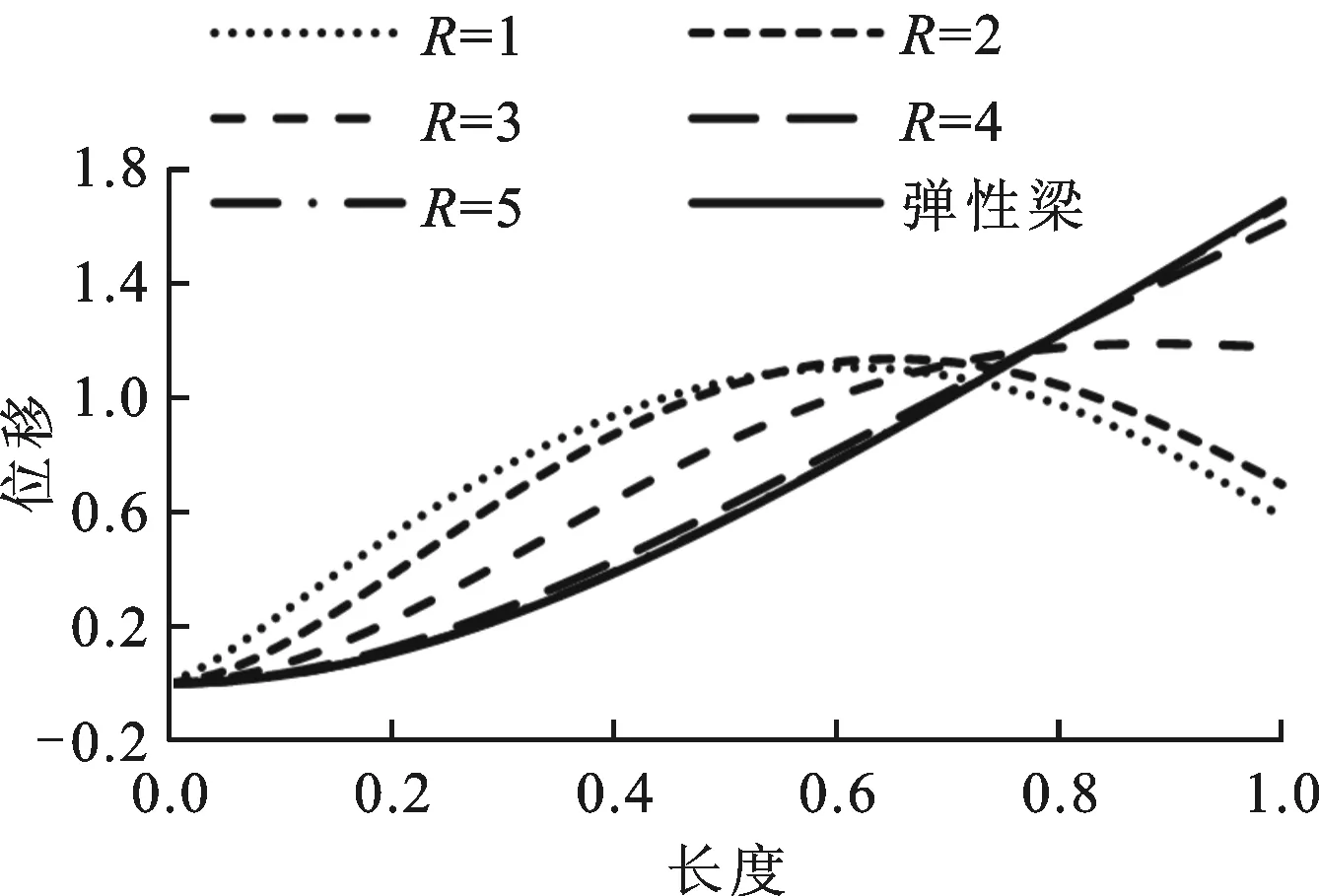
(a)第1阶振型

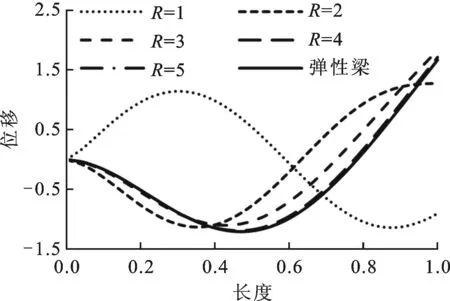
(b)第2阶振型

(c)第3阶振型

本文的研究结果表明,当虚拟弹性体的弹性模量小于等于结构弹性模量的1.0×106倍时,虚拟弹性体对弹性梁固有频率及振型的影响均可忽略。如果虚拟弹性体弹性模量取值过小,会超出计算机的精度范围,造成浮点溢出。因此,本文建议虚拟弹性体弹性模量的取值如下

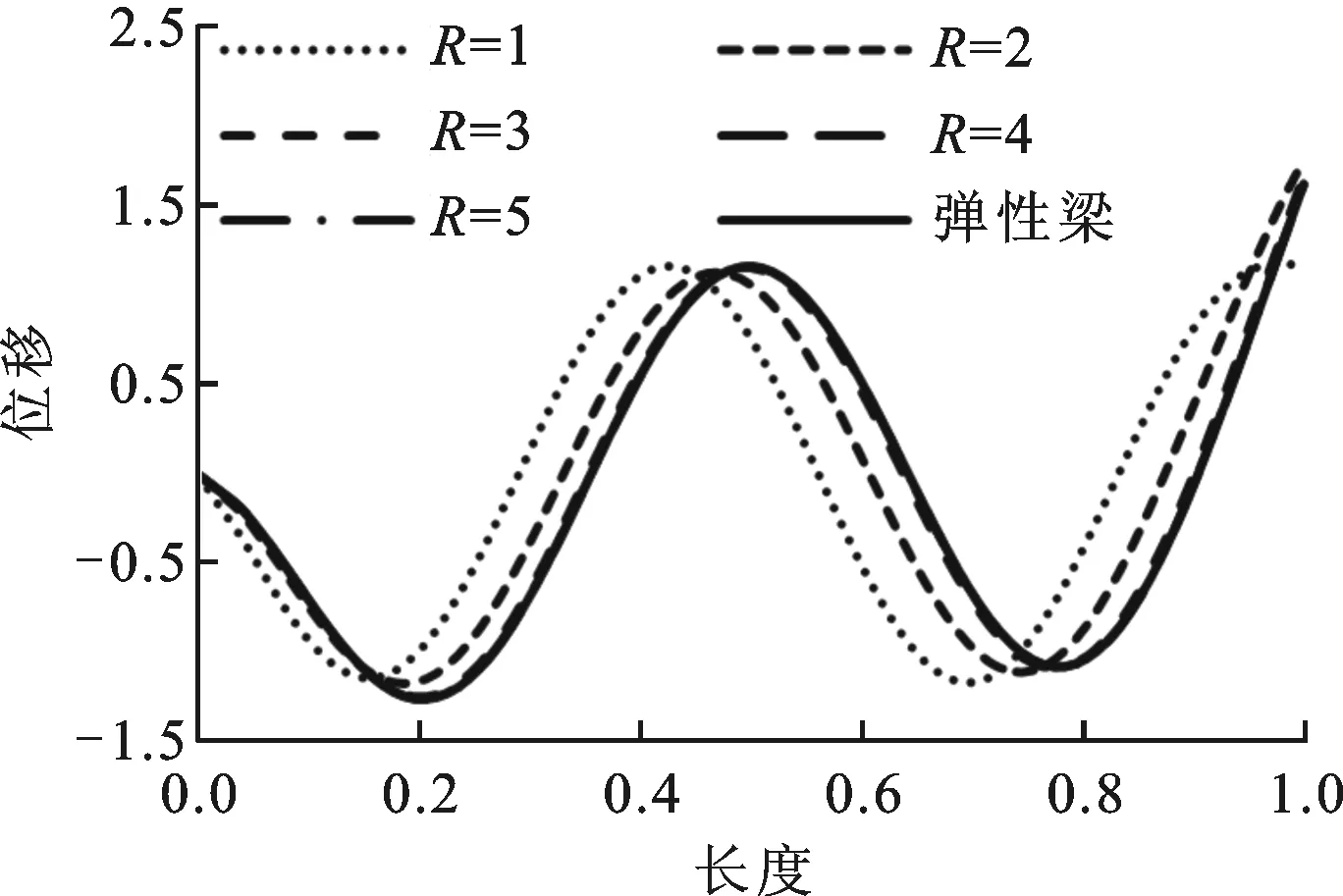
(d)第4阶振型图4 模态振型与弹性模量比对数的关系

(20)

此时,弹性梁及虚拟弹性体整体系统的各阶固有模态的振型见图5。

(a)第1阶模态

(b)第2阶模态

(c)第3阶模态

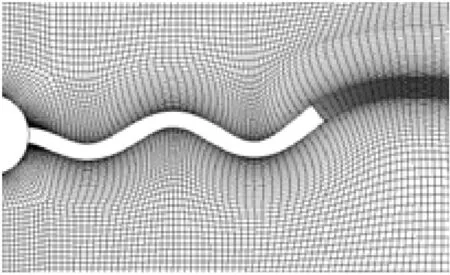
(d)第4阶模态图5 不同模态下的流场网格变形

2.2 流固耦合响应分析

本文以定常流场的结果作为瞬态流场的初值,采用该动网格算法对弹性梁颤振问题进行分析。设定时间步长为0.001 s,流场变量的相对残差随迭代步变化的曲线见图6。流场变量的相对残差减小,在进行25步迭代之后,残差基本保持不变。

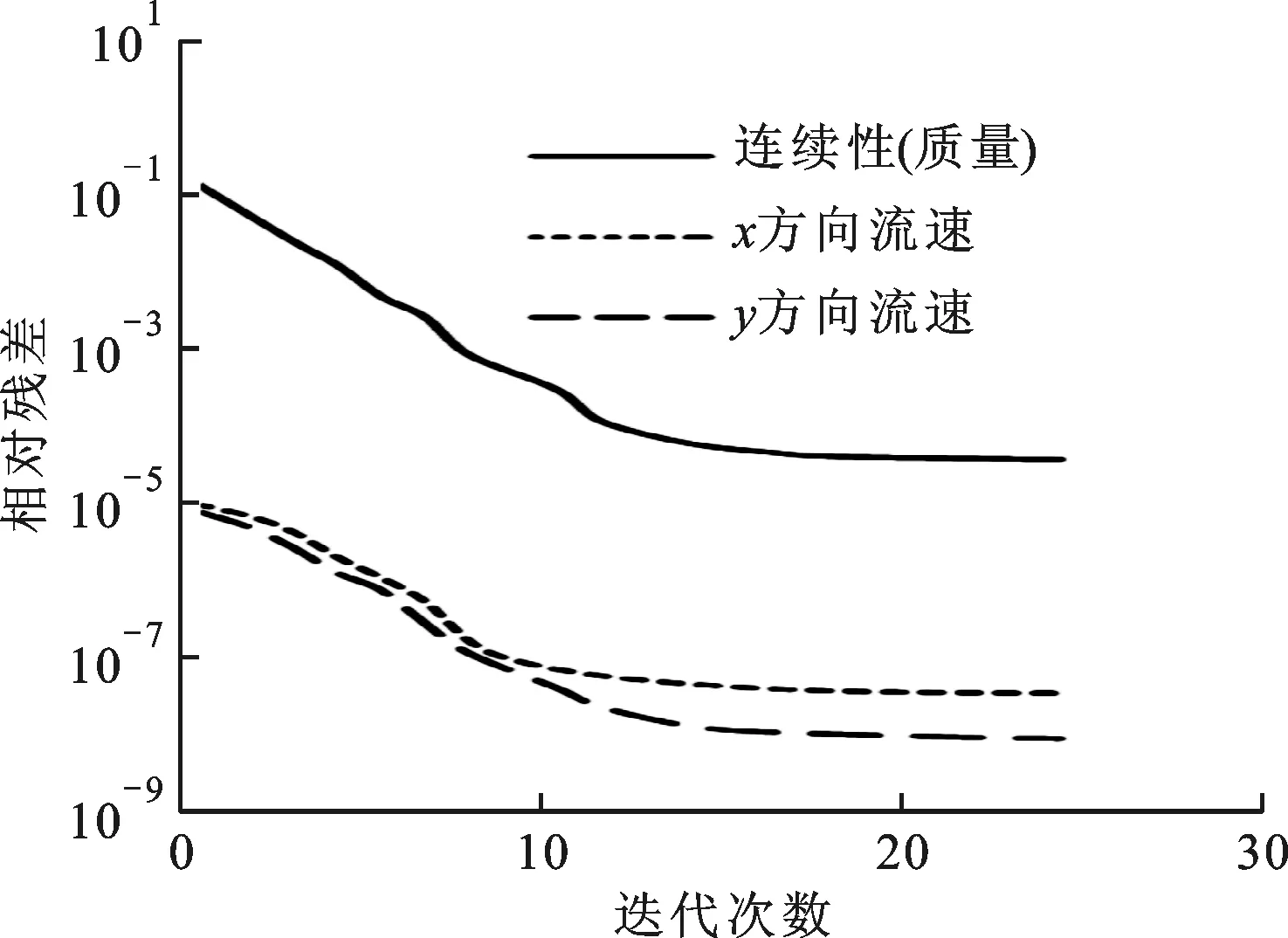
图6 流场变量相对残差与迭代次数的关系

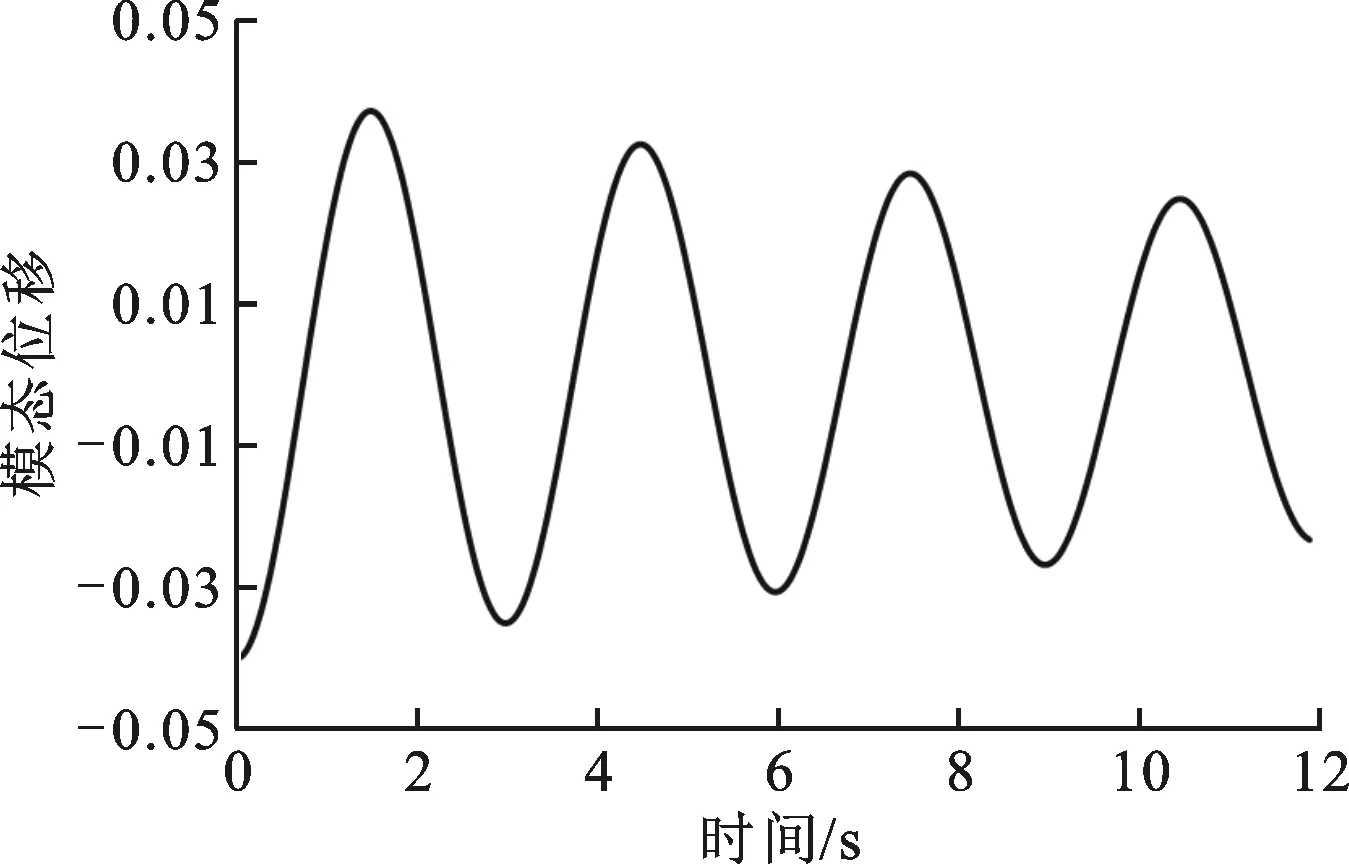
(a)第1阶

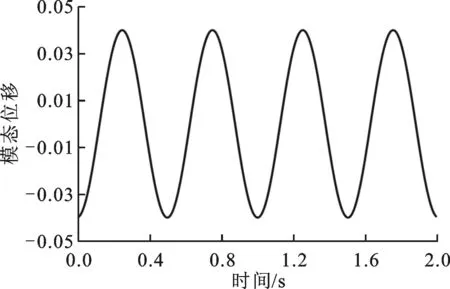
(b)第2阶

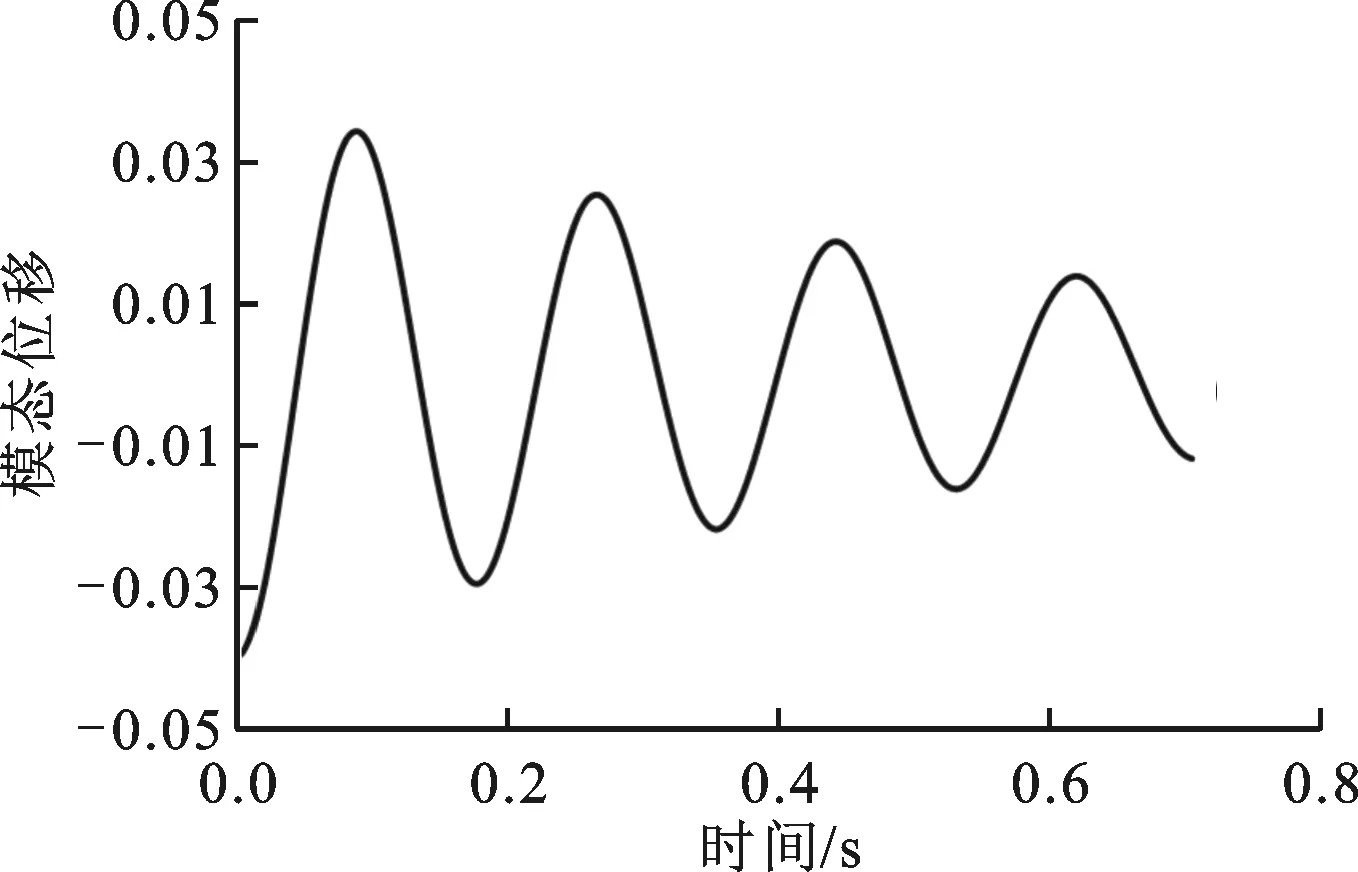
(c)第3阶

(d)第4阶图7 弹性梁的模态位移时间曲线

本文所采用的流动条件正是文献[13]中弹性梁颤振的流动条件。在此流动条件下,本文计算得到的弹性梁振动的模态位移与时间曲线见图7,模态位移为质量归一化量。随着时间的推进,第1阶,第3阶和第4阶振动的模态位移幅值逐渐减小,即不会发生颤振。第2阶模态振动的位移幅值不随时间变化,即第2阶模态的振动处于颤振临界点。该弹性梁的颤振为第2阶弯曲颤振。

(d)T图8 振动弹性梁附近的流场

采用流固耦合的方法,计算得到弹性梁右端中点的位移和时间曲线见图9,从中可以看出,本文的计算结果与文献[13]的结果吻合很好,验证了本文动网格算法的正确性。本文计算得到图9所示的弹性梁颤振的位移时间曲线,总耗时为19.8

h

。在相同计算条件下,采用传统弹性体网格变形方法

[10]

的计算时间为57.4

h

,而本文方法可以减少计算时间65.5%。

为进一步验证本文算法,我们对Wing445.6模型[14]的颤振问题进行了流固耦合分析,计算得到的颤振边界与实验值吻合良好,计算结果见图10,与已有弹性体方法相比,计算时间减少了54.8%。

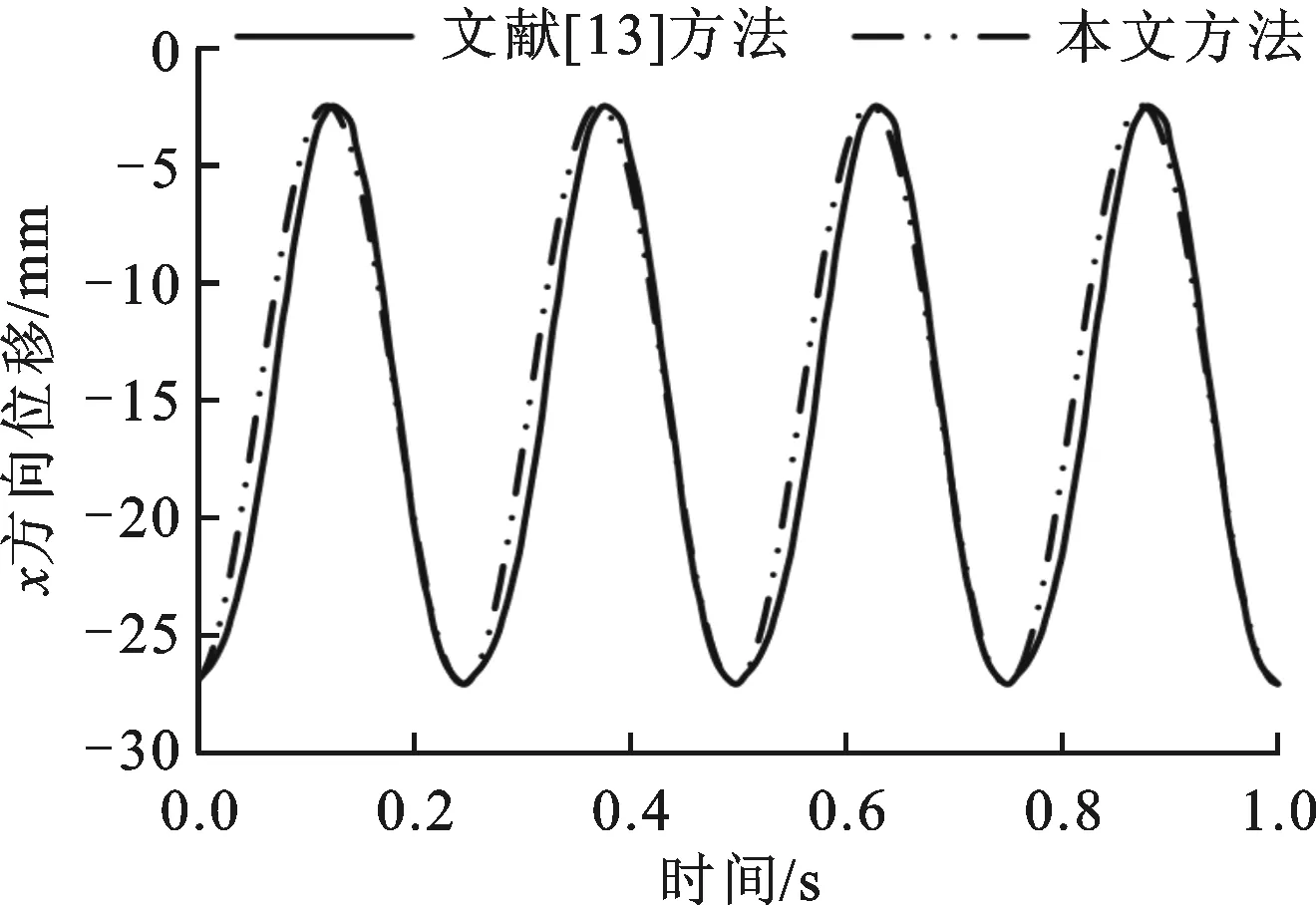
(a)x方向位移

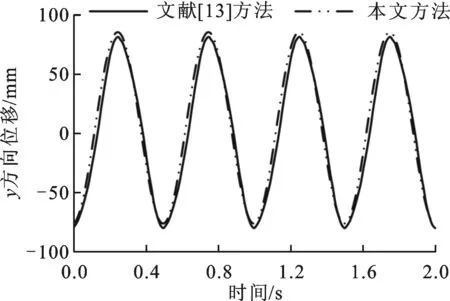
(b)y方向位移图9 弹性梁右端中点的位移和时间的关系

图10 Wing 445.6模型的颤振边界

3 结 论

本文提出了一种基于虚拟弹性体的快速动网格方法。将流场网格所包围的空间区域视为虚拟弹性体,并与结构一起,视为一个整体系统,以结构受到的流体作用力为激励,通过振型叠加法计算结构网格及流场网格节点的位移。考虑到实际结构的流固耦合振动多为低阶模态的振动,在流固耦合计算中可以通过低阶模态的叠加计算流场网格节点的位移,从而达到快速更新流场网格的目的。采用该方法对弹性梁颤振问题进行了流固耦合分析,计算结果与文献的结果吻合很好。与已有弹性体方法相比,本文算法可以减少合计算时间65.5%。研究发现,流场涡旋的周期性形成、发展及脱落是弹性梁颤振的主要原因。对Wing445.6模型颤振问题进行了分析,得到颤振边界与实验值吻合良好,且与已有弹性体法相比,可以减少计算时间54.8%。

[1] 张伟伟, 高传强, 叶正寅. 气动弹性计算中网格变形方法研究进展 [J]. 航空学报, 2014, 35(2): 303-319. ZHANG Weiwei, GAO Chuanqiang, YE Zhengyin. Progress on mesh deformation in computational aeroelasticity [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 303-319.

[2] 史爱明, 杨青, 杨永年. 非结构运动网格下的三维机翼颤振数值分析 [J]. 振动与冲击, 2006, 24(6): 27-28. SHI Aiming, YANG Qing, YANG Yongnian. Numerical flutter analysis of a 3-D wing using unstructured dynamic mesh Euler method [J]. Journal of Vibration and Shock, 2006, 24(6): 27-28.

[3] TEZDUYAR T E. Stabilized finite element formulations for incompressible flow computations [J]. Advances in Applied Mechanics, 1991, 28: 1-44.

[4] 陈炎, 曹树良, 梁开洪, 等. 基于温度体模型的动网格生成方法及在流固耦合振动中的应用 [J]. 振动与冲击, 2010, 29(4): 1-5. CHEN Yan, CAO Shuliang, LIANG Kaihong, et al. A new dynamic grids based on temperature analogy and its application in vibration engineering with fluid-solid interaction [J]. Journal of Vibration and Shock, 2010, 29(4): 1-5.

[5] 谢亮, 徐敏, 张斌, 等. 基于径向基函数的高效网格变形算法研究 [J]. 振动与冲击, 2013, 32(10): 141-145. XIE Liang, XU Min, ZHANG Bin, et al. Space points reduction in grid deforming method based on radial basis functions [J]. Journal of Vibration and Shock, 2013, 32(10): 141-145.

[6] TEZDUYAR T E, BEHR M, MITTAL S, et al. A new strategy for finite element computations involving moving boundaries and interfaces-the deforming-spatial-domain/space-time procedure: I The concept and the preliminary tests [J]. Computer Methods in Applied Mechanics and Engineering, 1992, 94(3): 339-351.

[7] TEZDUYAR T E, BEHR M, MITTAL S, et al. A new strategy for finite element computations involving moving boundaries and interfaces-the deforming-spatial-domain/space-time procedure: II Computation of free-surface flows, two-liquid flows, and flows with drifting cylinders [J]. Computer Methods in Applied Mechanics and Engineering, 1992, 94(3): 353-371.

[8] BAR-YOSEPH P Z, MEREU S, CHIPPADA S, et al. Automatic monitoring of element shape quality in 2-D and 3-D computational mesh dynamics [J]. Computational Mechanics, 2001, 27(5): 378-395.

[9] STEIN K, TEZDUYAR T, BENNEY R. Mesh moving techniques for fluid-structure interactions with large displacements [J]. Journal of Applied Mechanics, 2003, 70(1): 58-63.

[10]HUO S H, WANG F S, YAN W Z, et al. Layered elastic solid method for the generation of unstructured dynamic mesh [J]. Finite Elements in Analysis and Design, 2010, 46(10): 949-955.

[11]ZIENKIEWICZ O C, PAUL D K, HINTON E. Cavitation in fluid-structure response with particular reference to dams under earthquake loading [J]. Earthquake Engineering & Structural Dynamics, 1983, 11(4): 463-481.

[12]MARSHALL J G, IMREGUN M. A review of aeroelasticity methods with emphasis on turbomachinery applications [J]. Journal of Fluids and Structures, 1996, 10(3): 237-267.

[13]TUREK S, HRON J. Proposal for numerical benchmarking of fluid-structure interaction between an elastic object and laminar incompressible flow [M]. Berlin, Germany: Springer, 2006: 371-385.

[14]YATES E C, Jr. AGARD standard aeroelastic configurations for dynamic response I-wing 445.6 [R]. Neuilly Sur Seine, France: Advisory Group for Aerospace Research and Development Neuilly-Sur-Seine, 1988: 1-74.

(编辑 杜秀杰 赵炜)

An Efficient Dynamic Mesh Method Based on Pseudo Elastic Solid

ZHONG Jize1,2,XU Zili1,2,TAO Lei3

(1. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University,Xi’an 710049, China; 2. School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China;3. State Grid Zhejiang Beilun No.1 Power Generation Co. Ltd., Ningbo, Zhejiang 315800, China)

To reduce the computing time of fluid structure coupling, an efficient dynamic mesh method based on the pre-existing elastic solid method is developed. The flow mesh domain is assumed to be a pseudo elastic solid according to the basic hypotheses of the elastic solid method, then the structure and the pseudo elastic solid are considered together as one holistic system. Subsequently the natural frequencies and vibration modes are calculated for the system and the flow force acted on the structure is considered as the excitation of the holistic system. The nodal displacements for the structure and the flow mesh are computed by mode superposition. In fact, the actual fluid structure coupled vibration for structures often appears associated with low order modes, the nodal displacements of the flow mesh can be calculated by modal superposition of the first few of low order modes, thus the flow mesh can be updated efficiently. A beam flutter problem is discussed with the present dynamic mesh method. The results coincide well with the data reported in the existing reference verifying the validation of the present method. The computing time is reduced by 65.5% compared with the pre-existing elastic solid method. The flutter of wing 445.6 is also analyzed and the calculated flutter boundary agrees with the experimental data, and the computing time is reduced by 54.8%.

fluid structure interaction; elastic solid method; efficient dynamic mesh method

2016-03-22。

仲继泽(1988—),男,博士生;徐自力(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(51275385)。

时间:2016-07-14

http:∥www.cnki.net/kcms/detail/61.1069.T.20160714.1719.002.html

10.7652/xjtuxb201610020

O323;O351.2

A

0253-987X(2016)10-0132-07