快速多特征金字塔的尺度目标跟踪方法

杨源,库涛,查宇飞,张园强,李寰宇

(1.空军工程大学空管领航学院,710051,西安;2.空军工程大学航空航天工程学院,710038,西安)



快速多特征金字塔的尺度目标跟踪方法

杨源1,库涛2,查宇飞2,张园强2,李寰宇1

(1.空军工程大学空管领航学院,710051,西安;2.空军工程大学航空航天工程学院,710038,西安)

为了克服目标尺度变化导致的跟踪失败问题,提出了一种快速多特征金字塔的尺度目标跟踪算法。该算法融合了梯度特征和颜色特征,提高了特征表征的维度,以便获得更多的目标表征信息;同时利用多尺度特征金字塔快速地近似相邻尺度特征,得到不同尺度模板,从而平衡了由于特征维度上升带来的计算时间开销,并保证了近似的准确性; 在相关滤波框架下,综合不同尺度模板的跟踪结果,实现对目标位置和尺度的准确估计。选取4个具有尺度变化、光照变化和背景干扰的典型场景视频序列进行仿真实验,结果表明,与传统的尺度自适应核跟踪算法相比,提出的跟踪算法能够很好地适应外部环境变化,实现对尺度目标的鲁棒跟踪,同时在中心位置误差、覆盖率、精确度和成功率4个指标上优于对比算法。

目标跟踪;相关滤波;尺度自适应;快速特征金字塔

(1. School of Air Control and Navigation, Air Force Engineering University, Xi’an 710051, China;2. School of Aeronautics and Astronautics Engineering, Air Force Engineering University, Xi’an 710038, China)

视觉目标跟踪[1-3]是计算机视觉中非常重要的一个分支,被广泛应用于视频监视、人机交互和无人驾驶等领域。视觉目标跟踪解决的基本问题是给定初始帧目标的位置和尺度,快速准确地寻找到目标在接下来的视频中的位置和大小。然而,因为尺度、旋转和形变等内因以及背景干扰、光照等外因相互作用,目标外观会改变,使得目标跟踪容易发生漂移,甚至失败。

相关滤波算法因其具有较高的跟踪精度和较少的时间开销,引起了相关学者们的研究兴趣。文献[4]提出了一种自适应的最小平方误差和输出(MOSSE)的相关滤波算法,实现了目标的快速鲁棒跟踪,但该算法特征较为简单,不适用于复杂场景。由于基于循环结构的核相关滤波(KCF)跟踪算法[5-6]采用了核映射,使得用较为简单的特征也能取得较好的跟踪效果,但它不具有尺度自适应性。文献[7]在MOSSE的基础上采用更为复杂的梯度方向直方图(HOG)[11]特征,并加入尺度自适应性,使得跟踪性能进一步提升,并夺得视觉2014年目标跟踪挑战(VOT2014)第1名。文献[8]在KCF的基础上融合HOG特征和颜色属性特征,提高了目标表征的维度,取得很好的跟踪性能,但计算量较大,为平衡性能,尺度搜索空间较小,导致尺度估计并不优于判别式尺度空间跟踪器(DSST)。

基于以上考虑,本文提出一种快速多特征金字塔的尺度目标跟踪算法,能够克服目标尺度变化所导致的跟踪失败问题。该算法融合梯度特征和颜色特征,以便获得更多的目标表征信息;同时利用多尺度特征金字塔快速地近似相邻尺度特征,克服了因特征维度增加而导致的多尺度特征计算量增大的问题;在相关滤波框架下,综合不同尺度模板的跟踪结果,实现对目标位置和尺度的准确估计。

1 核相关滤波跟踪

核相关滤波应用于跟踪,本质上是一个多实例学习的过程,通过密集采样遍历目标可能出现的位置,并采用高斯函数作为对应的空间响应分布,从而采用岭回归模型训练得到一个滤波器,用该滤波器对下一帧图像滤波,响应最大点位置即为目标位置。利用循环矩阵与傅里叶变换的性质[9]加快滤波器的训练速度,引入核函数[10]将低维特征映射到高维,提高了特征表征的鲁棒性。

1.1 核岭回归模型

相关滤波的根本目的在于学习一个滤波器w来最小化一系列训练样本{x1,x2,…,xn}经滤波后的响应函数f(w;xi)与期望输出响应yi之间的误差,一般取f(w;x)=wTx,即为

(1)

式中:λ为正则化项,避免过拟合,取为0.01。X=(x1,x2,…,xn)T,Y=(y1,y2,…,yn)T,其中yi为顶点在目标中心处的高斯函数。式(1)的解析解为

w=(XHX+λI)-1XHY

(2)

(3)

(4)

式(4)可变为

(5)

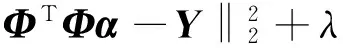
(6)

其解析解为

α=(K+λI)-1Y

(7)

式中:K为n×n的核矩阵,且Ki,j=φT(xi)φ(xj),易知K为循环矩阵[6],即K=C(kxx),其中kxx为核矩阵K的第一行。选取高斯核函数,则有

(‖x‖2+‖x′‖2)-

(8)

由循环矩阵的性质以及式(3)、式(4),利用傅里叶变换,得到α的频域解为

(9)

由文献[6]可知,式(7)的结论同样适用于样本xi和期望输出响应yi为二维信号的情况。从而针对跟踪问题,可以利用上一帧学习到的滤波器α对当前帧图像滤波,找到目标响应最大处,即为目标在当前帧的位置。

1.2 目标响应函数

下一帧的样本z的响应函数为

f(z)=wTz=αTΦTz=(Kz)Tα=(C(kxz))Tα

(10)

由式(3)、式(4),式(8)的傅里叶变换为

(11)

对目标的位置更新为

(12)

对式(12)求时域响应最大点的位置,从而确定目标中心点的位置,实现位置更新。

2 本文跟踪方法

2.1 特征融合

(13)

综合考虑不同特征的差异性,本文选取融合梯度方向直方图(HOG)特征[11]和颜色属性(CN)特征[12]来描述目标外观。其中,HOG描述的是目标的形状特征,通过提取图像的梯度信息并统计梯度方向直方图,有31个通道,选取的计算单元尺寸为1;CN描述的是目标的颜色特征,是由文献[12]提出的一种基于语义颜色标签的特征,有11个通道。直接融合HOG特征和CN特征,对特征进行多通道的拼接,使得目标的特征维度达到42个,因而在计算不同尺度的图像特征时,需要用到本文采用的快速特征金字塔的计算方法。

2.2 快速特征金字塔

文献[13]提出了一种基于统计规律的快速特征金字塔的计算方法,可以大大减少计算特征的时间,提高效率,用于目标检测取得了很好的效果。其基本方法可以表述为

Xs≈R(X,s)s-λΩ;X=Ω(I)

(14)

式中:I为原始图像;X为特征图像;s表示尺度;Ω(·)为特征提取函数;R(X,s)为重采样函数,表示将特征图X按尺度s进行重采样;Is为原始图像I在尺度s采样的结果。λΩ为特征估计参数,可由两个不同尺度的特征图像近似如下

λΩ=lb(Ω(Xs1)/Ω(Xs2))/lb(s1/s2)

(15)

传统特征金字塔的方法是先构建图像金字塔,后计算每层的特征,本文提出用单幅图像的特征估计不同尺度的特征,从而大大加快特征计算时间。本文特征提取方法与传统方法对比如图1所示。

(a)传统特征金字塔提取方法

(b)本文特征金字塔提取方法图1 两种特征金字塔计算方法对比

2.3 跟踪框架

基于上述核相关滤波算法和快速多尺度特征计算方法,本文提出一种基于快速特征计算的多尺度核相关滤波算法。首先通过快速特征计算,得到多尺度的特征模板;其次用不同尺度的模板分别进行学习得到多尺度滤波器;最后用这些多尺度滤波器对下一帧图像进行滤波,查找响应最大值所对应的位置和尺度,实现尺度自适应跟踪,其基本框架见图2。

图2 本文跟踪算法流程图

图3 不同的尺度模板获取方法示意图

(2)基于多模板的跟踪方法。相关滤波实质上仍然是一个模板匹配的问题,通过模板与待检测的图像进行相关操作,得到不同位置的响应值,训练模型可表示为求解下式

(16)

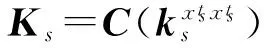
(17)

从而检测下一帧图像z中目标的响应函数为

(18)

目标位置和尺度更新可通过求解下式获得

(19)

(3)模型更新。由于本文将模板最终进行了尺寸扩充,将较小的模板按边缘像素进行复制,将较大的模板进行截取,保证尺寸的一致性,从而可以很方便地进行更新。本文选取初始帧目标尺寸的2.5倍作为模板尺寸,更新公式可表示为

(20)

3 实验结果及分析

本文的仿真实验均在CPU为Intel Core i3-4150、主频为3.50 GHz、8 GB内存的计算机环境下通过MATLAB2013a软件平台进行实现,并选取核循环结构跟踪器算法(CSK)[5]、KCF[6]、DSST[7]、正则化互相关算法(NCC)[14]、基于核的结构化输出跟踪方法(Struck)[15]、多示例学习算法(MIL)[16]、增量跟踪方法(IVT)[17]和本文算法的实验结果和性能进行定性和定量的分析。

3.1 定性分析

为了对比各算法的性能,从OTB2013数据库中选取了4个典型的序列进行验证,各个序列的特点如表1所示,其跟踪结果如图4所示。

表1 典型视频序列描述

由图4的结果可以看出,本文算法在尺度变化、光照变化、姿态变化、遮挡和复杂背景下能够实现尺度目标的鲁棒跟踪。Doll序列具有目标尺度变化、复杂背景干扰、快速移动等特点,本文算法能够实现对目标的鲁棒跟踪。Shaking序列具有较为强烈的光照变化,本文算法采用了更为复杂的特征表示方法,能克服强光照带来的影响。Trellis序列具有很强的光照及阴影变化,本文算法采用的高维特征和多模板跟踪的方法能够实现这种复杂情况下的鲁棒跟踪。Walking序列具有目标较小且有姿态变化等特点,本文算法能实现准确跟踪。

图4 Doll、Shaking、Trellis、Walking跟踪结果示意图

3.2 性能分析

本文从中心位置误差、覆盖率、精确度和成功率4项性能指标和计算复杂度等5个方面,对本文算法和6种对比算法进行评估。

3.2.1 跟踪性能

(1)中心位置误差。中心位置误差[18]计算如下

c=(‖O-Ot‖2)1/2

(21)

式中:O和Ot分别为算法得到的目标中心点坐标和人工标定的目标中心真实坐标。中心位置误差的单位为像素,表示两点间距离像素点的个数。中心位置误差可以衡量算法中心位置的跟踪性能,其值越小,表明中心位置跟踪误差越小,性能越高。视频中每帧的中心位置误差如图5所示,平均中心位置误差见表2。不难看出,本文算法与其他6种算法相比,具有较低的中心位置误差。

(2)覆盖率。覆盖率[18]是检测目标与真实目标重叠部分与两者的并集之比,表示为

(a)Doll序列

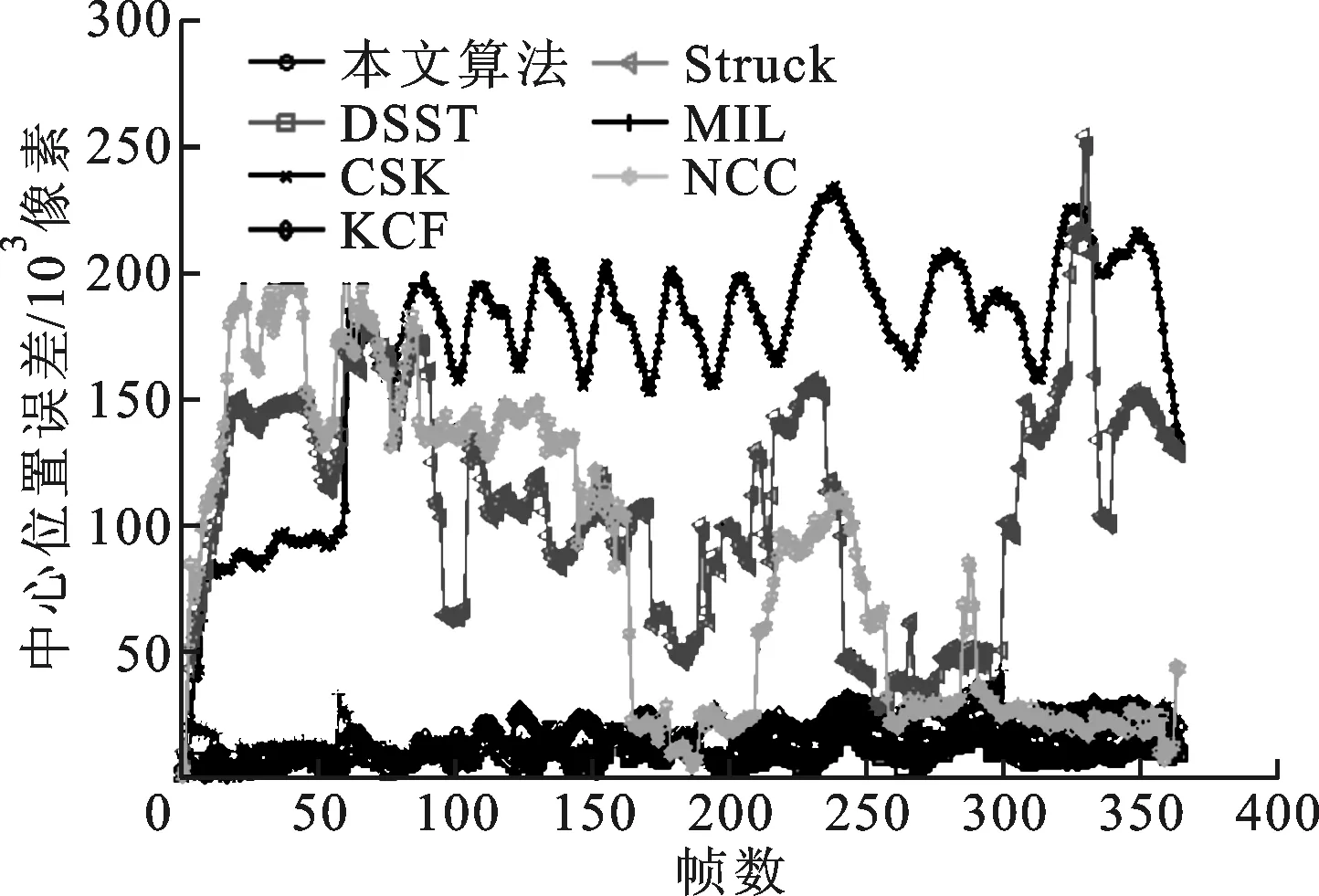
(b)Shaking序列

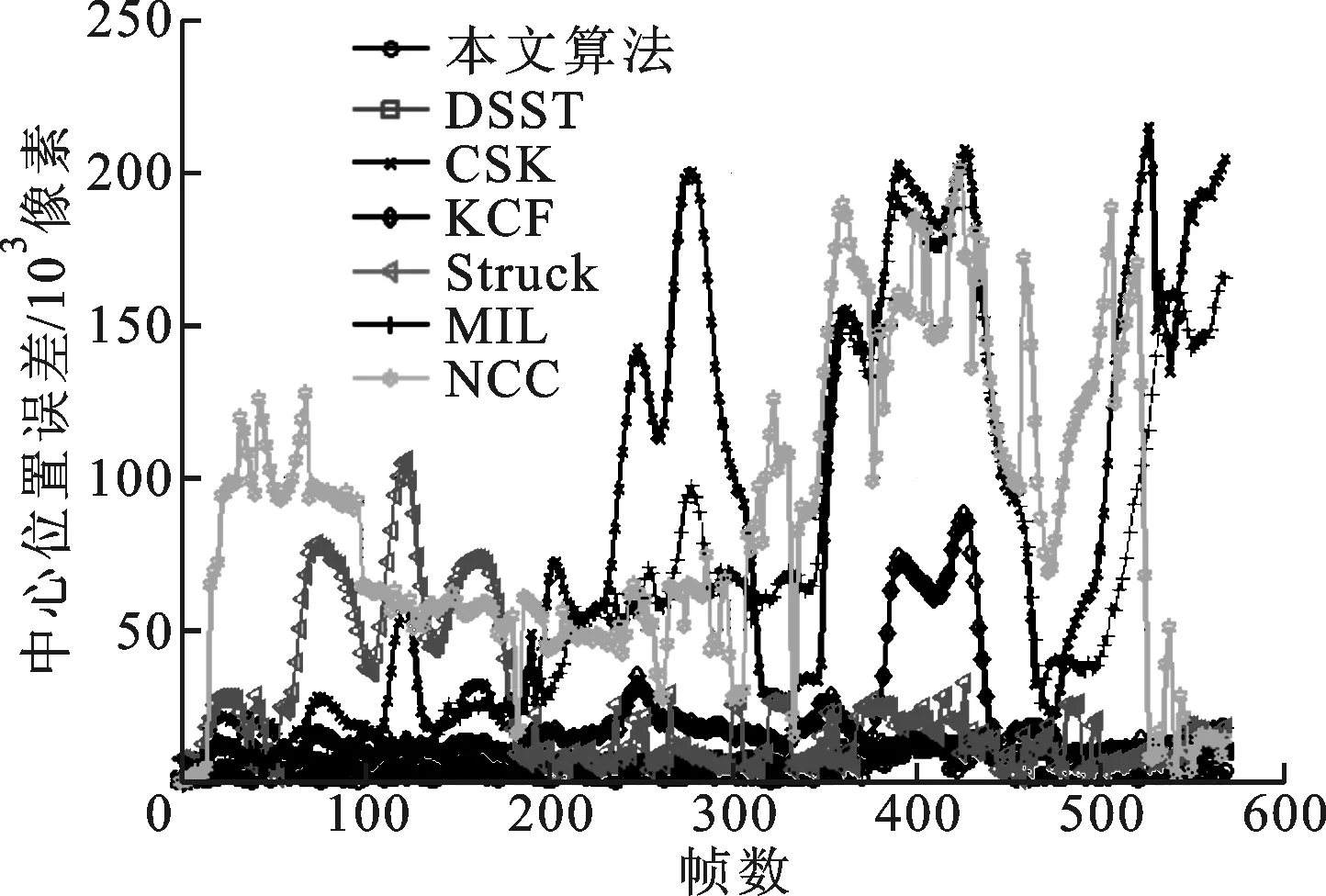
(c)Walking序列

(d)Trellis序列图5 各算法跟踪结果的中心位置误差比较

(22)

(a)Doll序列

(b)Shaking序列

(c)Trellis序列

(d)Walking序列图6 各算法跟踪结果的覆盖率比较

(3)精确度。精确度[18]表示跟踪结果与跟踪误差的关系,曲线越陡,表示跟踪精度越高。公式如下

(23)

注:*表示最优结果;**为次优结果。

式中:Df表示第f帧的跟踪结果与真实值之间的中心位置误差;α表示取中心位置误差的阈值。精确度与中心位置误差的关系如图7所示。不难看出,在4个典型视频中,本文算法具有更好的中心位置跟踪性能。

(a)Doll序列

(b)Shaking序列

(c)Trellis序列

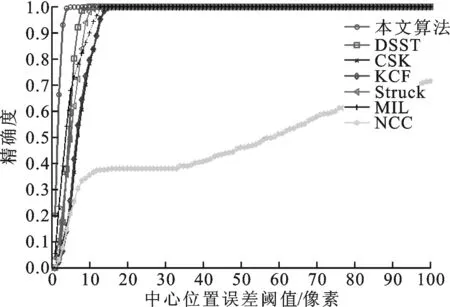
(d)Walking序列图7 各算法跟踪结果的精确度比较

(4)成功率。成功率表示跟踪结果与跟踪覆盖率的关系,即覆盖率大于特定阈值的视频帧占总帧数的比例,曲线越陡,表示跟踪精度越高。成功率计算如下

(24)

式中:Lf表示第f帧的跟踪结果与真实值之间的覆盖率;α表示取覆盖率的阈值。图8为成功率与不同覆盖率阈值的关系,它表明当取不同覆盖率阈值时,成功跟踪的视频帧数占总帧数的比例。不难看出,本文算法具有更高的成功率,性能更好。

(a)Doll序列

(b)Shaking序列

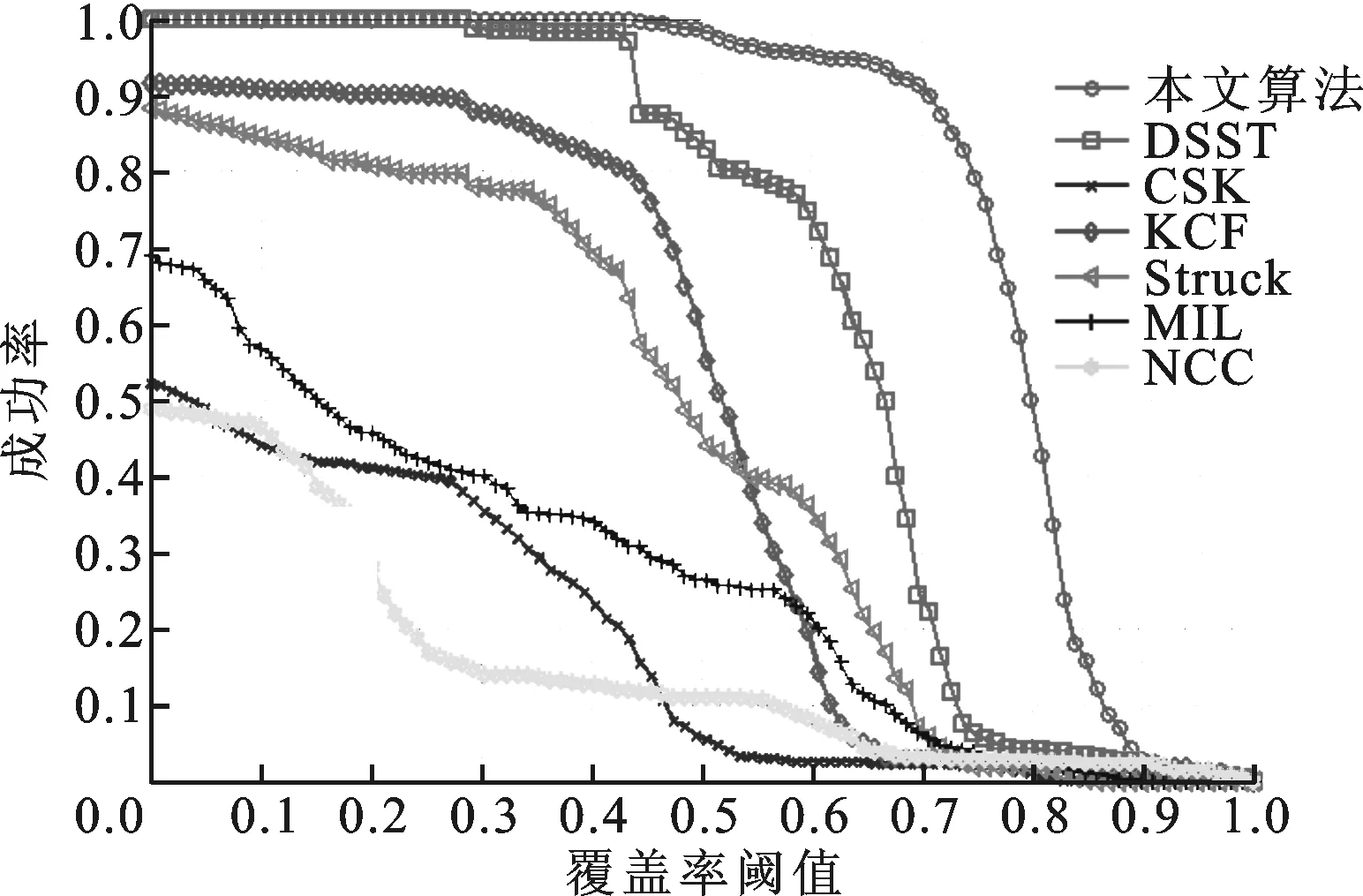
(c)Trellis序列

(d)Walking序列图8 各算法跟踪结果的成功率比较

3.2.2 算法复杂度 本文算法的复杂度主要体现在高维特征和多尺度模板相关滤波跟踪导致的计算量的增加,和快速尺度估计使得计算量的减少。为了更直观地表现本文算法的复杂度,比较了7种算法在4个典型视频序列上的处理速度,结果如表3所示,从中可以看出本文算法实现了跟踪的实时性。

表3 各算法计算速度的比较

4 结 论

本文提出了一种特征融合的快速尺度目标跟踪算法。主要创新点体现在:采用多特征融合的方式提高目标表征的维度,增加跟踪的鲁棒性;利用快速特征金字塔来解决因维度增大而带来的计算量增大的问题;采用多模板的相关滤波方法来解决尺度跟踪的问题。实验结果表明,本文算法能够快速而准确地实现尺度目标的实时跟踪。

[1] 查宇飞, 杨源, 王锦江, 等. 利用密度描述符对应的视觉跟踪算法 [J]. 西安交通大学学报, 2014, 48(9): 13-18. ZHA Yufei, YANG Yuan, WANG Jinjiang, et al. A visual object tracking algorithm using dense descriptors correspondences [J]. Journal of Xi’an Jiaotong University, 2014, 48(9): 13-18.

[2] 库涛, 毕笃彦, 杨源, 等. 尺度目标的频域核回归跟踪研究 [J]. 空军工程大学学报(自然科学版), 2016, 17(2): 76-81. KU Tao, BI Duyan, YANG Yuan, et al. Scalable object tracking based on frequency kernel regression [J]. Journal of Air Force Engineering University (Natural Science Edition), 2016, 17(2): 76-81.

[3] 毕笃彦, 库涛, 查宇飞, 等. 基于颜色属性直方图的尺度目标跟踪算法研究 [J]. 电子与信息学报, 2016, 38(5): 1099-1106. BI Duyan, KU Tao, ZHA Yufei, et al. Scale-adaptive object tracking based on color names histogram [J]. Journal of Electronics and Information Technology, 2016, 38(5): 1099-1106.

[4] BOLME D S, BEVERIDGE J R, DRAPER B, et al. Visual object tracking using adaptive correlation filters [C]∥IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ, USA: IEEE, 2010: 2544-2550.

[5] HENRIQUES J F, CASEIRO R, MARTINS P, et al. Exploiting the circulant structure of tracking-by-detection with kernels [C]∥European Conference on Computer Vision. Berlin, Germany: Springer, 2012: 702-715.

[6] HENRIQUES J, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596.

[7] DANELLJAN M, HAGER G, KHAN F, et al. Accurate scale estimation for robust visual tracking [C]∥British Machine Vision Conference. Berlin, Germany: Springer, 2014: 1-4.

[8] LI Y, ZHU J. A scale adaptive kernel correlation filter tracker with feature integration [C]∥European Conference on Computer Vision. Berlin, Germany: Springer, 2014: 254-265.

[9] GRAY R M. Toeplitz and circulant matrices: a review [M]. San Francisco, USA: Now Publishers Inc., 2006: 89-101.

[10]SCHOLKOPF B, SMOLA A J. Learning with kernels: support vector machines, regularization, optimization, and beyond [M]. Boston, Massachusetts, USA: MIT Press, 2001: 57-61.

[11]FELZENSZWALL P F, GIRSHICK R B, MCALLESTER D, et al. Object detection with discriminatively trained part-based models [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1627-1645.

[12]VAN DE WEIJER J, SCHMID C, VERBEEK J, et al. Learning color names for real-world applications [J]. IEEE Transactions on Image Processing, 2009, 18(7): 1512-1523.

[13]DOLLAR P, APPEL R, BELONGIE S, et al. Fast feature pyramids for object detection [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(8): 1532-1545.

[14]YOO J C, HAN T H. Fast normalized cross-correlation [J]. Circuits, Systems and Signal Processing, 2009, 28(6): 819-843.

[15]HARE S, SAFFARI A, TORR P H S. Struck: structured output tracking with kernels [C]∥IEEE International Conference on Computer Vision. Piscataway, NJ, USA: IEEE, 2011: 263-270.

[16]BABENKO B, YANG M H, BELONGIE S. Visual tracking with online multiple instance learning [C]∥IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ, USA: IEEE, 2009: 983-990.

[17]POGGIO T, CAUWENBERGHS G. Incremental and decremental support vector machine learning [J]. Advances in Neural Information Processing Systems, 2001, 13(5): 409-412.

[18]BOUGUET J Y. Pyramidal implementation of the affine lucas kanade feature tracker description of the algorithm [J]. Intel Corporation Microprocessor Research Labs Tech Rep, 2000, 22(2): 363-381.

(编辑 杜秀杰)

Fast Multi-Feature Pyramids for Scale-Adaptive Object Tracking

YANG Yuan1,KU Tao2,ZHA Yufei2,ZHANG Yuanqiang2,LI Huanyu1

A fast scale estimation algorithm for visual tracking with feature integration is proposed to solve tracking failure from object scale changes. The gradient feature and color feature are integrated to obtain more object representation information with the increasing feature dimensions, then a fast multi-scale feature pyramid method is used to approximate the adjacent scale features to get templates in different scales, thus it is possible to balance the computation cost due to the increasing feature dimensions without accuracy loss after approximation. Combining tracking results of multi-scale templates, the object location and scale are estimated accurately by the proposed algorithm in the framework of correlation tracking 4 representative video sequences with scale changes, and illumination variations and background clusters are chosen to simulate. The experiments indicate that the proposed algorithm well adapts to environmental variations and outperforms the traditional scale-adaptive kernel correlation tracking schemes in center location error, overlap ratio, precision and success rate.

object tracking; correlation filtering; scale-adaptive; fast feature pyramids

2016-01-18。

杨源(1982—),男,副教授。

国家自然科学基金资助项目(61472442);陕西省科技新星资助项目(2015kjxx-46)。

时间:2016-07-14

http:∥www.cnki.net/kcms/detail/61.1069.T.20160714.1726.016.html

10.7652/xjtuxb201610008

TP391

A

0253-987X(2016)10-0049-08