采用聚类特征的基本概率分配生成方法及应用

高智勇,董荣光,高建民,王荣喜

(西安交通大学制造系统工程国家重点实验室,710049,西安)



采用聚类特征的基本概率分配生成方法及应用

高智勇,董荣光,高建民,王荣喜

(西安交通大学制造系统工程国家重点实验室,710049,西安)

针对在识别框架不确定时基本概率分配(BBA)生成困难的问题,提出一种基于聚类特征的基本概率分配生成方法,以减弱对样本长度的依赖性,并分析2种情况下的BBA生成。在框架未知时,通过聚类分析获得各个类别的聚类特征,建立样本属性的聚类特征区间模型;在框架已知时,获取聚类特征,建立样本属性的聚类特征区间模型;然后用各个区间模型之间的距离表示样本属性之间的差异,在此基础上建立了一种相似度的度量方法;最后对相似度进行归一化得到BBA。采用Iris数据集和Wine数据集的实验结果表明:所提方法对样本长度敏感程度低,对Wine数据集的一个类的分类结果达到100%。将该方法应用于某煤化工企业压缩机组子系统状态监测信息数据集,实现了监测信息状态的识别。

证据理论;基本概率分配;聚类特征区间模型;相似度;信息融合

利用提取的特征识别系统监测信息状态时,由于每种特征在表述状态信息时都有一定的不确定性甚至获得冲突的结论,如何综合利用多源特征信息、消除冲突成为了研究的热点之一。决策级信息融合依据相应准则和决策的可信度,综合利用主观信息及客观信息等,完成最优决策的制定。决策级信息融合方法有贝叶斯推理、模糊理论和D-S证据理论等,证据理论由于其可满足比概率论和贝叶斯推理更弱的条件,具有直接表达“不确定”和“不知道”的优势,使得证据理论在机械/电子系统的故障诊断等领域获得了广泛的应用。

Dempster-Shafer(D-S)证据理论产生子上世纪60年代,由Dempster提出集值映射的概念,并诱导和定义了上、下概率[1]。Shafer利用信度函数对上、下概率重新诠释,创立了证据的数学理论[2];韩崇昭教授进一步研究了D-S的研究进展和方向[3]。在使用D-S证据理论进行信息融合的应用时,为了使用证据理论的组合规则,首先要生成基本概率分配(basic belief assignment, BBA)[4-9],而对于如何生成合适的BBA,与D-S组合规则一起成为D-S证据理论研究中的2个开放的话题,尚无一致的结论。

总体来看,BBA的生成分为2种模式,一种是专家经验打分,一种是根据统计特征自动生成BBA。由于专家背景知识的差异性以及主观性强的特点,往往会出现证据高度冲突的情况[10-11],因此基于统计分析的BBA自动化生成方法得到更为广泛的应用。韩崇昭教授在文献[12]中提出了一种在最大熵原则下生成BBA的方法;Bi等针对文本分类问题设计了三焦元组BBA[13];Deng等提出了基于回转半径而得到相似度,进而得出了BBA的方法[14];文献[15]提出一种基于随机集理论讲模糊传感器报告生成BBA并提出一种基于证据距离的融合方法。

分析现有的BBA生成方法,可以看出:BBA对样本的完备性依赖性较强,要求样本具有相对完备的信息,同时要求样本长度要满足一定要求,但在流程生产系统中,系统状态信息呈现出海量性以及系统状态不可穷举的特点,具有分析意义的信息表现出强烈的不平衡性。因此,对目标属性进行K-means聚类分析,可以在识别框架未知的情况下,完成目标属性的D-S信息融合,同时信息融合的结果对样本长度依赖程度较低。在对目标属性的聚类特征获取的基础上,本文提出了一种新的BBA生成方法,用聚类特征之间的距离来衡量目标之间的差异性,获得相似度,进而得到基本信度分配。这种方法能应用于识别框架未知或者样本长度变化的场合。

1 基本理论

1.1 D-S证据理论

D-S证据理论作为一种不确定性推理方法,为决策级不确定信息的表征与融合提供了强有力的工具。与证据理论直接相关的若干概念介绍如下。

(1)辨识框架,用Θ表示。辨识框架是由一个有空而完备的样本空间组成,组成取决于研究人员能知道什么和期望知道什么,任何一个关注的部分都成为识别框架的一个子集。对于Θ中元素,要求两两之间排斥,且包含研究中所要识别的全部对象。

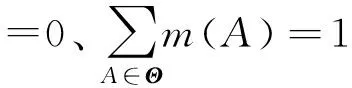
(3)焦元。对于识别框架中任一子集A,如果满足m(A)>0,则称A为焦元。一个mass函数的所有焦元的集合组成为mass函数的核。

(4)Dempster组合规则。m1和m2分别是同一框架下来自2个不同信源的基本信度赋值组合,Dempster组合规则定义为

(1)

(2)

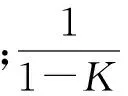
1.2 K-means聚类特征

聚类分析能够有效从数据中发现有用的信息,所获取的特征能较好反映所在簇的特点。聚类研究已经有数十年的历史,所产生的聚类方法很多,简单划分为基于层次的方法[16]、基于划分的方法[17]、基于密度的方法[18]等。李阳阳等提出一种基于流行距离的相似度衡量聚类算法,提高了未知对象隶属度划分的准确性,并提出了一种新的衡量相似性的聚类特征[19],以期获得全局的描述,并进一步在文献[20]中将该种聚类算法应用于SAR图像处理中。从算法研究程度和工程应用上,K-means算法是典型的基于划分的方法,并在研究和工程应用中得到了更多的检验。本文使用经典K-means算法进行聚类特征的获取,聚类特征区间模型组成形式为[ci,cr],其中ci为聚类中心,cr为聚类半径。以下将分别对2种情形进行讨论。

(1)识别框架未知。使用K-means对获得的样本数据首先进行聚类分析,获得K个类别。提取每个类别(簇)的聚类特征,组成相应的区间模型。

(2)识别框架已知。该种情形最为简洁,直接对样本数据进行处理,建立每个样本属性的聚类特征区间模型。

2 新的BBA生成方法

本节将提出基于聚类特征区间的BBA生成方法。在BBA的生成过程中,涉及到待识别样本与模型样本之间的相似度,本节将首先提出衡量两者之间相似度的方法,之后详细说明BBA的生成过程。

2.1 聚类特征相似度

设F1=[ci1,cr1]和F2=[ci2,cr2]是2个单元素焦元,则它们之间的相似距离定义为

D2(F1,F2)=(ci1-ci2)2+(cr1-cr2)2

(3)

2个聚类特征模型之间的相似度定义为

(4)

式中:α>0是支持系数,其主要作用是调节生成相似度数值的离散程度,尤其是对于由于值相对集中(精度原因)造成的误差。

从相似度的定义可以看出:当两模型相等时,S(F1,F2)=1;当两者的差异越大,则计算得出的相似度值就越小;同样可以得出S(F1,F2)=S(F2,F1)。

2.2 BBA生成步骤

用聚类特征区间模型生成BBA的过程是:首先用收集到的样本特征构造区间模型;然后求待测样本与模型区间的距离,并在此基础上获得两者的相似度计算值;最后对相似度进行归一化生成BBA。过程的具体步骤如下:

(1)建立样本特征属性的聚类特征区间模型;

(2)计算待识别样本属性值与模型区间之间的距离;

(3)计算待识别样本属性值与模型区间之间的相似度;

(4)对相似度进行归一化,生成BBA。

对于多元素的焦元,即焦元中包含多于一个元素的情况,此时往往由于样本属性在单元素焦元之间具有存在重叠部分,对于该重叠部分聚类特征区间模型的处理详见2.3节。

2.3 多元素焦元的聚类特征区间

本节以3个模型(即3个单元素焦元)为例说明对存在交集多元素焦元的区间模型生成。

设F1=[ci1,cr1],F2=[ci2,cr2]和F3=[ci3,cr3]为3个单元素焦元,对于焦元{F1,F2}、{F1,F3}、{F2,F3}和{F1,F2,F3}的聚类特征区间模型,其获取过程如图1所示。

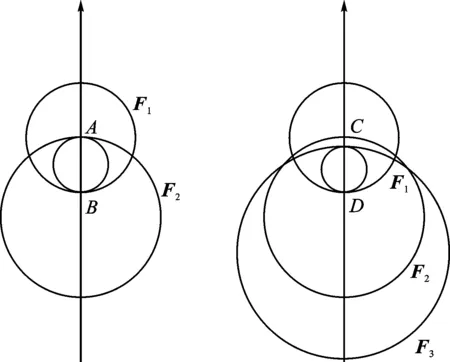
(a)双元素焦元交集 (b)三元素焦元交集图1 多元素交集示意图

以{F1}、{F2}两者交集和{F1,F2,F3}三者交集为例,计算多元素焦元的聚类特征区间模型。

(1){F1}、{F2}两者交集为{F1,F2},两者交于A和B2点,过A、B2点的圆即为交集的聚类区间模型,如图1a所示,则交集的聚类中心与聚类半径分别为

(5)

(6)

因此,焦元{F1,F2}的聚类特征区间模型为[ci,AB,cr,AB]。

(2){F1}、{F2}、{F3}三者交集为{F1,F2,F3},3个焦元的聚类区间交于C和D2点,过C、D2点的圆即为三者交集的聚类区间模型,则三者交集的聚类中心与聚类半径为

(7)

(8)

则焦元{F1,F2,F3}的聚类特征区间模型为[ci,CD,cr,CD]。

(3)对于不存在交集的其他焦元,统一规定为[0,0]。遇到该类型的焦元进行下一步的计算时,应该排除在外。

2.4 关于方法的若干讨论

(1)聚类特征是文中所提方法的基础,其有效性对BBA结果的可信性有较大影响。文中采用K-means聚类方法,针对以下2种情况:一是识别框架未知而数据集已获得的情况,通过合理确定初始类个数k和聚类中心予以聚类特征有效的保证;二是识别框架已知情况,聚类特征的有效性主要依靠合理确定聚类中心和聚类半径予以保证。

(2)若聚类特征提取不很有效,造成其表征该状态下的特征集的能力有限,衡量不同类相似性的能力有限,对BBA生成效果有影响。针对该类问题的解决方法,应研究合适的聚类特征提取方法,本文所应用的K-means聚类算法不仅能处理小样本数据,同时也能处理大样本数据,所提取的聚类特征具有很强表征能力。

(3)证据理论中BBA的生成原则在于未知样本与已知样本集之间相似性的衡量,目前各研究方法的不同之处多在于衡量相似性的方法不同。基于距离衡量相似性是研究应用比较多而且工程适用性比较强的一类方法。本文提出的相似度衡量方法是对欧氏距离取倒数,保证最终相似性计算结果小于1,同时保证了未知样本与识别框架中每个焦元的差异性衡量,方法简洁、便于工程计算,因此具有较强实用性和有效性。

(4)对于BBA的生成,使用本文中的相似度衡量方法能满足应用和研究需要。文中使用的相似度是基于距离的相似度,尚未考虑角度相似度。给予后续研究启示:虽然衡量样本相似度的方法和研究较多,选取有效的相似度衡量方法是非常重要的。

3 数据及结果分析

以下将使用Iris和Wine数据集对上述方法进

行验证,并对不同训练样本情况下的Dempster信息融合结果对比,并对Wine分类结果做分析,实例分析了某煤化工企业压缩机组子系统的状态信息。

3.1 Iris数据的BBA生成

Iris数据集[21]共有3个种类,分别是Setosa、Versicolor、Virginica,简记为Se、Ve、Vi。数据集有150个样本,其中每个种类有50个样本。每类都有4个属性特征描述,分别是Sepal Length、Sepal Width、Petal Length和Petal Width,特征属性分别简记为SL、SW、PL、PW。BBA生成步骤如下。

步骤1 生成聚类特征区间模型。对于这3个种类的Iris,都随机选择20个样本,建立它们的区间模型。每个种类下都随机选取一个样本,作为测试样本。聚类特征区间模型如表1所示。

步骤2 求待测样本与模型属性之间的距离Ls。把待测样本的属性值作为聚类特征区间模型,例如Ls=4.5可以看成区间[4.5,0]。在计算的距离基础上,获得待测样本与模型属性之间的相似度(此时支持系数取为1),相似度及BBA计算结果如表2所示。

步骤3 对求得的相似度进行归一化,获得基本信度分配结果,如表2所示。

步骤4 Dempster-Shafer信息融合及决策分析。共有3个待测样本,分别是S1:{5.4,3.4,1.7,0.2};S2:{5.9,3.2,4.8,1.8};S3:{6.9,3.2,5.7,2.3}。每个焦元的融合结果及待测样本决策分析如表3所示。

数据集的聚类特征能够实现较好的基本概率分配 (即mass函数的获取),并且经过D-S决策级信息融合后的结果显示,未知样本能够准确归属于已知的类别。

3.2 样本数量变化下的Iris融合结果分析

本节将探索在不同样本数据量情况下本文方法的有效性,将采用3.1节的{5.4,3.4,1.7,0.2}作为测试样本,变化训练样本长度。样本的规模依次为20,25,30,35,40,45,对经过D-S信息融合后的结果进行对比分析,结果见表4。

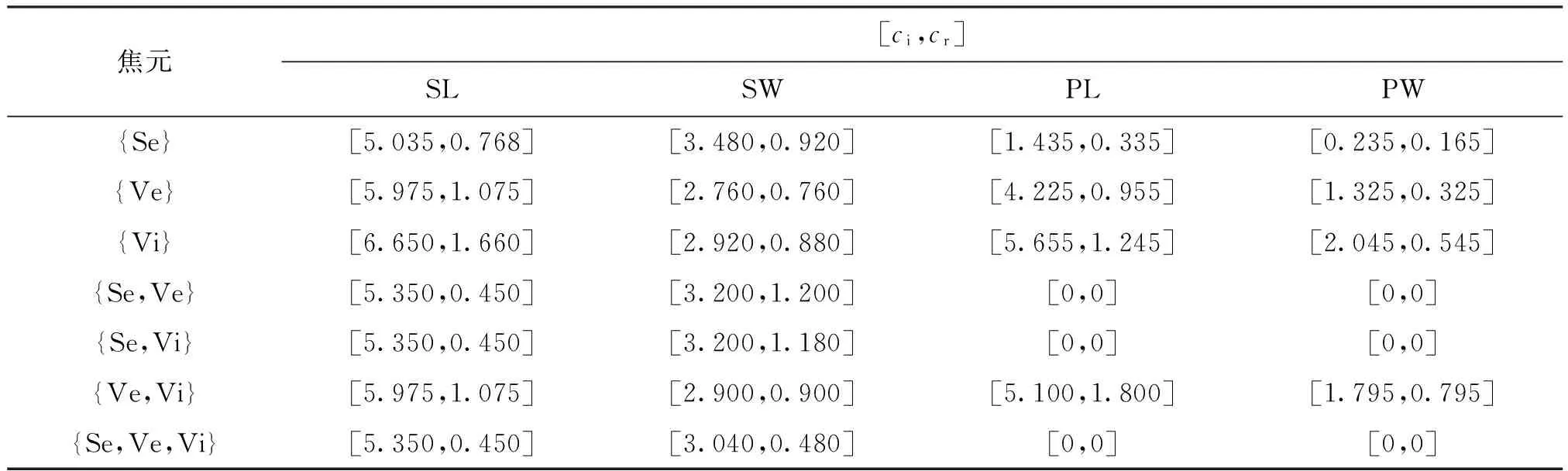
表1 4种特征属性的聚类特征区间模型

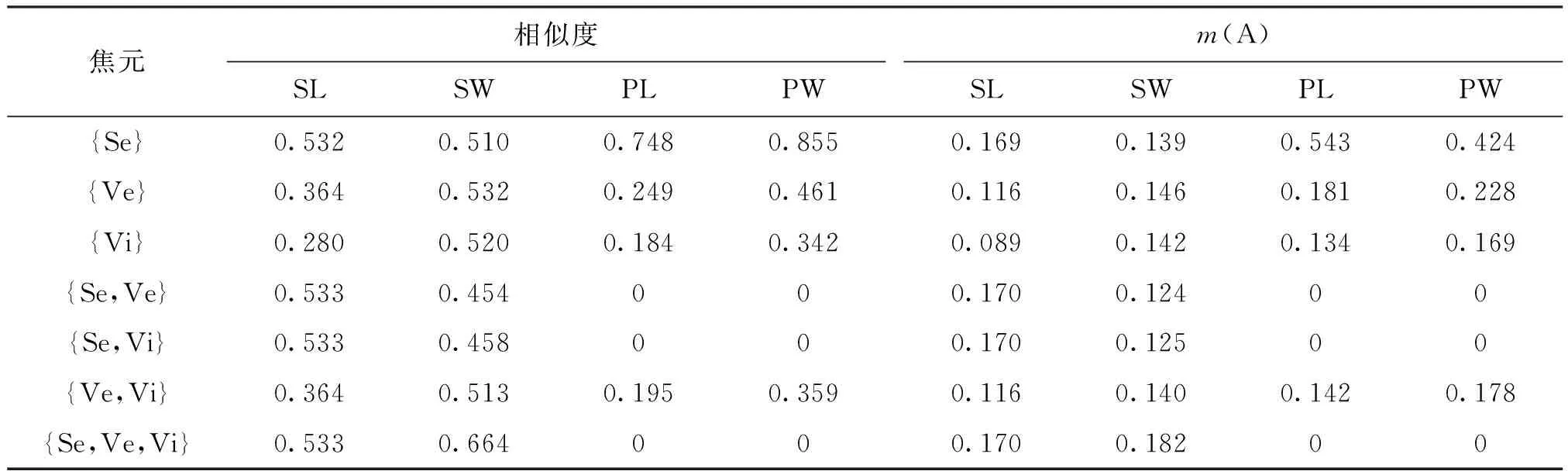
表2 相似度及BBA计算结果(以Setosa为例)

表3 每个焦元的融合结果及待测样本决策分析

表4 不同样本长度的D-S信息融合结果对比

表4结果显示,基于K-means聚类特征的BBA生成方法对样本数据量不敏感。K-means方法不仅对于分析小样本具有很好的表现,对于处理较大样本同样具有很好的表现,因此可同时进行处理大数据量样本以及小样本数据。文献[4]同样可以处理小样本数据,对于处理大样本数据,聚类特征能更好表征样本的特性。

3.3 Wine数据集分类结果

Wine数据集共有3类,分别简记为C1、C2和C3,对应的每个类的数据样本数为59、71和48,样本的字符数为178,每个类有13个属性。采用本文的BBA生成方法,对C1的59个样本应用证据理论进行分类(其他2类计算过程相似)。同时,为了说明本文所提BBA生成方法的稳健性,只选取Malic acid和Flavanoids这2个属性。

采用本文基于聚类特征的BBA生成方法,选择待测样本为{1.810,2.910},应用证据组合规则计算每个焦元的信度函数,即[m(C1),m(C2),m(C1,C2),m(C1,C3),m(C2,C3),m(C1,C2,C3),m(∅)=[0.334,0.188,0.199,0.112,0.725,0.066 5,0.018 7],从而得出决策分析结果:待测样本准确归属为C1。

对C1类的59个样本重复上述过程,计算分类结果及误分的样本数量。其中C1的59个样本准确归属为C1类,分类正确率为100%。

应用本文BBA生成方法对C1类中59个样本决策级的信息融合结果表明:59个样本被准确分到C1类中,准确率达到100%。但是,在计算C1中第22个样本时,决策向量中{C1}和{C3}的信度函数值相差较小,为0.042 3,因此后续研究中需要研究更好的聚类特征提取方法,以适应研究和工程应用的需要。

3.4 某煤化工压缩机组子系统状态信息

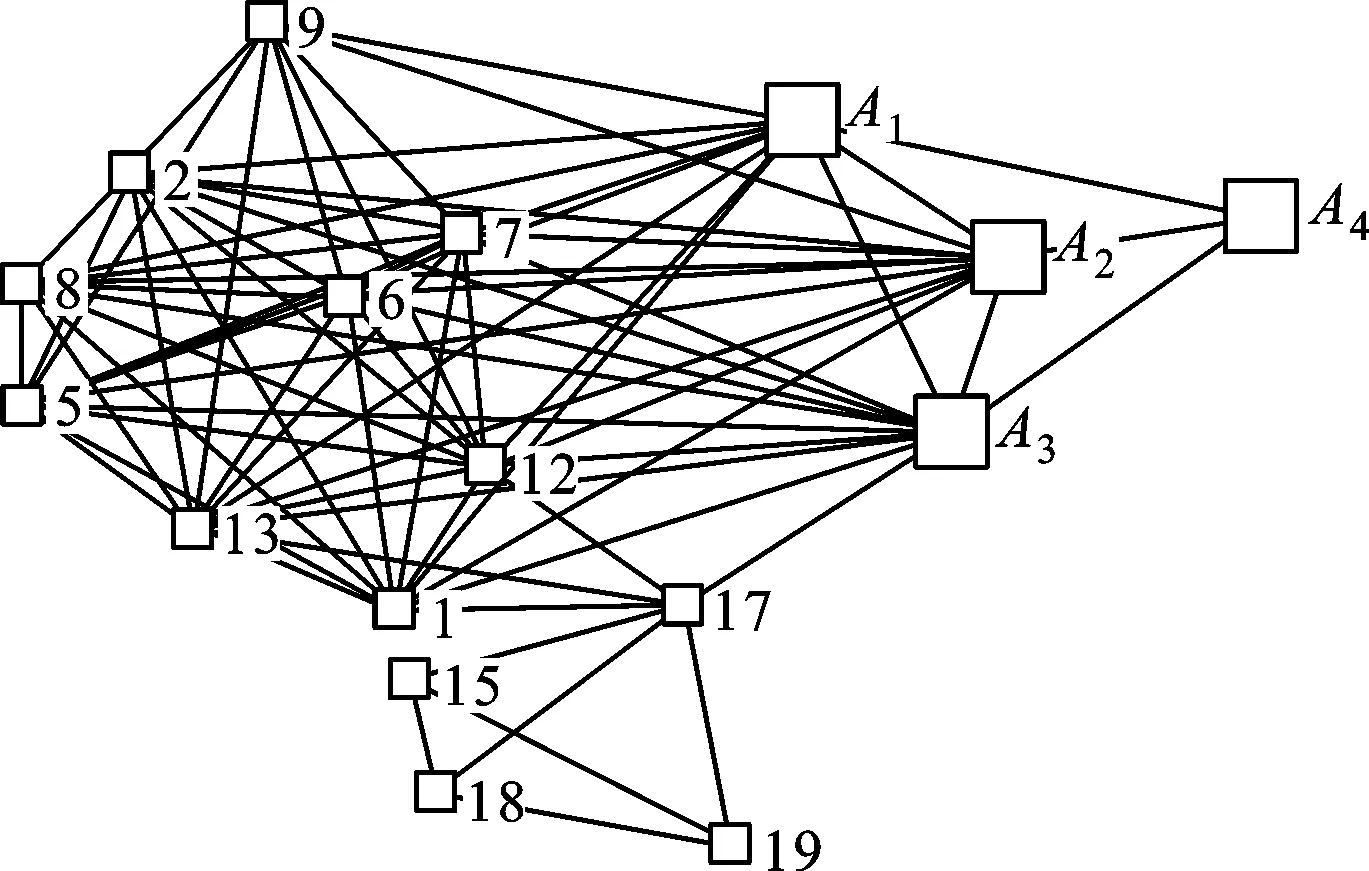
图2 压缩机组子系统部分变量耦合关系网络

应用本文的BBA生成方法及证据组合规则,识别某煤化工集团压缩机组系统的状态。该系统是由油路、蒸汽冷凝、空压机、增压机和轴系等子系统构成的分布式复杂机电系统,是典型的非线性系统。由于系统不能进行重复性或破坏性试验,研究应用替代数据法模拟A1点位高于设定值(高报警)、低于设定值(低报警)和设定值微波动(正常)3种状态下的监测信息序列,选取与A1耦合的监测点位A2、A3和A4(连接关系见图2,依据监测信息序列间长程幂率相关建立网络模型)。采用本文的BBA生成方法及证据组合规则所得到的决策结果如表5所示。

每种监测信息状态下获取A1的监测信息序列及其他3个点位的监测信息序列。每个耦合关系提取Kendall秩相关系数、互信息及DCCA指数[22],进行D-S信息融合。分别对每种监测信息序列状态截取20组样本数为2 000的序列,提取耦合特征,建立耦合特征矩阵。

对系统中的任何监测点位,3种监测信息状态组成完备的识别框架。按照基于区间数获得每一个证据的BBA,形式表现为对每个焦元分配的BBA值,例如SL表示赋予低报警状态的基本信度分配BBA值;对于空集的BBA值赋予0。由于每种状态需要足够多的典型故障案例数据,而实际生产中往往不能满足这种要求,因此这里使用替代数据法对正常监测信息序列的部分进行替换,产生多组异常信息序列。

表5 采用本文方法所得到的决策结果

计算结果表明,第1个决策向量对监测信息的正常状态支持程度为0.393 8,第2个决策向量对监测信息的高报状态支持程度为0.510,第3个决策向量对监测信息的低报状态支持程度为0.503。在存在证据冲突的情况下,D-S证据融合的结果对于这些状态的判断基本是正确的。D-S决策级信息融合考虑了监测信息序列的非线性特征,区分多种监测信息的状态。需要注意的是:监测信息高于设定值和低于设定值的信度函数计算结果比较接近,后续研究中可针对该类型的问题,研究更为合适的聚类特征。

4 结 论

采用聚类特征描述不确定性信息时对样本数据量不敏感,并且对于处理大样本时聚类特征能够更好表征样本属性,同时通过调整支持系数使D-S融合结果的更为有效。对于识别框架未知的情形,通过聚类分析同样可以获得每一类别的聚类特征区间模型,实现基于D-S的信息融合和决策分析。Iris数据集的D-S信息融合结果验证了本文方法的有效性,Wine数据集的分类结果说明本文方法的稳健性,最后分析某煤化工企业压缩机组子系统监测信息的状态识别,使得该方法相对简单、易行,适用于工程应用。后续的研究将针对Dempster-Shafer组合规则的研究及改进和更有效的聚类特征提取方法,为流程工业生产系统状态监测信息状态识别结果及检测耦合关系的冲突,实现监测信息准确性评价奠定基础。

[1] DEMPSTER A P. Upper and lower probabilities induced by a multiple value mapping [J]. The Annals of Mathematical Statistics, 1967, 38(2): 325-339.

[2] SHAFER G. A mathematical theory of evidence [M]. Princeton, NJ, USA: Princeton University Press, 1976: 1-30.

[3] 韩德强, 杨艺, 韩崇昭. DS证据理论研究进展及相关问题探讨 [J]. 控制与决策, 2014, 29(1): 1-11. HAN Deqiang, YANG Yi, HAN Chongzhao. Advances in DS evidence theory and related discussions [J]. Control and Decision, 2014, 29(1): 1-11.

[4] 康兵义, 李娅, 邓勇, 等. 基于区间数的基本概率指派生成方法及应用 [J]. 电子学报, 2012, 40(6): 1092-1096. KANG Bingyi, LI Ya, DENG Yong, et al. Determination of basic probability assignment based on interval numbers and its application [J]. Acta Electronica Sinica, 2012, 40(6): 1092-1096.

[5] HAN D Y, DEZERT J, HAN C Z. New basic belief assignment approximations based on optimization [C]∥15th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2012: 282-293.

[6] ZHU J, YAN M L, WANG C X, et al. New construction approach of basic belief assignment based in confusion matrix [J]. Research Journal of Applied Sciences, Engineering and Technology, 2012, 4(16): 2716-2722.

[7] 李云彬, 李辉, 王云飞. 基于模糊数相似性的BPA生成方法 [J]. 现代电子技术, 2011, 34(15): 5-7. LI Yunbin, LI Hui, WANG Yunfei. BPA generation method based on the similarity of fuzzy numbers [J]. Modern Electronics Technique, 2011, 34(5): 5-7.

[8] 周哲. 证据理论中证据生成和融合方法研究 [D]. 杭州: 杭州电子科技大学, 2011: 18-22.

[9] 文成林, 周哲, 徐晓滨. 一种新的广义梯形模糊数相似性度量方法及在故障诊断中的应用 [J]. 电子学报, 2011, 39(3): 1-6. WEN Chenglin, ZHOU Zhe, XU Xiaobin. A new similarity measure between generalized trapezoidal fuzzy numbers and its application to fault diagnosis [J]. Acta Electronica Sinica, 2011, 39(3): 1-6.

[10]何友, 王国宏, 陆大金, 等. 多传感器信息融合及应用 [M]. 北京: 电子工业出版社, 2001: 5-25.

[11]邓勇, 施文康, 朱振福. 一种有效处理冲突证据的组合方法 [J]. 红外与毫米波学报, 2004, 23(1): 27-32. DENG Yong, SHI Wenkang, ZHU Zhenfu. Efficient combination approach of conflict evidence [J]. Journal of Infrared and Millimeter Waves, 2004, 23(1): 27-32.

[12]韩崇昭, 韩德强, 介婧. 从生物感知认识到系统工程方法论 [J]. 系统工程理论与实践, 2008(S1): 75-95. HAN Changzhao, HAN Deqiang, JIE Jing. From biological cognition and perception to methodologies of system engineering [J]. System Engineering: Theory and Practice, 2008(S1): 75-96.

[13]BI Y X, BELL D, GUAN J W. Combining evidence from classifiers in text categorization [C]∥Proceedings of the 8th International Conference on Knowledge-Based Intelligent Information and Engineering Systems. Berlin, Germany: Springer-Verlag, 2004: 521-528.

[14]DENG Y, JIANG W, XU X, et al. Determining BPA under uncertainty environments and its application [J]. Chinese Journal of Electronics, 2009, 26(1): 13-17.

[15]DENG Y, SHI W K, ZHU Z F, et al. Combining belief function based on distance of evidence [J]. Decision Support System, 2004, 38(3): 389-493.

[16]ZHANG T, RAMAKRISHNANA R, OGIHARA M. An efficient data clustering method for very large databases [C]∥Proceeding of ACM-SIGMOD International Conference on Management of Data. New York, USA: ACM, 1996: 103-114.

[17]HUANG Z. Extensions to theK-means algorithm for clustering large data sets with categorical values [J]. Data Mining and Knowledge Discovery, 1998(2): 283-304.

[18]ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovery clusters in large spatial database [C]∥Proceedings of 2nd International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 1996: 266-231.

[19]李阳阳, 石洪竺, 焦李成, 等. 基于流行距离的量子进化聚类算法 [J]. 电子学报, 2011, 39(10): 2343-2347. LI Yangyang, SHI Hongzhu, JIAO Licheng, et al. Quantum-inspired evolutionary clustering algorithm based on manifold distance [J]. Acta Electronica Sinica, 2011, 39(10): 2343-2347.

[20]LI Y Y, FENG S X, ZHANG X R, et al. SAR image segmentation based on quantum-inspired multiobjective evolutionary clustering algorithm [J]. Information Processing Letters, 2014, 114(6): 287-293.

[21]Iris Data Set. Famous database for pattern recognition from Fisher[EB/OL]. (2011-03-20) [2016-01-05]. http: ∥archive.ics.uci.edu/ml/datasets/Iris.

[22]PODOBNIK B, STANLEY H E. Detrended cross-correlation analysis: a new method for analyzing two nonstationary time series [J]. Physical Review Letters, 2008, 100(8): 0814021.

(编辑 刘杨)

A Method to Generate Basic Belief Assignment Based on Clustering Analysis and Its Application

GAO Zhiyong,DONG Rongguang,GAO Jianmin,WANG Rongxi

(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A method to generate BBA (basic belief assignment) based on cluster analysis is proposed to focus the problem that the mass function is hard to determine when the frame is unknown. The method tackles the situation whether the frame of discernment is known or not. A clustering analysis method is applied to extract cluster features and models of cluster features are constructed with the samples. Then the distances between different cluster feature models are calculated to represent differences between sample attributes and then the similarities of them are obtained. Finally, the values of similarities are normalized to get the BBA. The analysis results of classifying the Iris dataset and Wine dataset show that the proposed method is less dependent on the length of samples and the classification accuracy in Wine dataset is 100%. Monitoring information series by applying the method to a compressor unit system proves the effectiveness of the method, and the condition of monitoring information can be clearly recognized.

evidence theory; basic belief assignment; cluster feature interval model; similarity; information fusion

2016-03-17。 作者简介:高智勇(1973—),男,副教授,博士生导师。 基金项目:国家自然科学基金资助项目(51375375)。

时间:2016-07-21

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160721.2215.014.html DOI:10.7652/xjtuxb201610002

TP391

A

0253-987X(2016)10-0008-07