拱架现浇拱圈混凝土拱桥的合理施工程序与方法

张玉平，彭毕辉，李传习，董创文

(长沙理工大学 土木与建筑学院，长沙 410114)



拱架现浇拱圈混凝土拱桥的合理施工程序与方法

张玉平，彭毕辉，李传习，董创文

(长沙理工大学 土木与建筑学院，长沙 410114)

针对目前确定拱架现浇拱圈混凝土浇筑顺序主要考虑拱架变形而未考虑结构应力的现状，以贵州甘河沟大桥主桥为工程背景，结合其原施工方案初步确定了分环分段位置，利用MIDAS软件对拱架现浇拱圈混凝土的施工全过程进行仿真分析，综合考虑拱架变形和结构应力，通过多方案计算对比确定了合理的最优浇筑方案：第1环混凝土浇筑顺序为先拱脚段再拱顶段最后中间段；第2环混凝土浇筑顺序为先拱顶段再拱脚段最后中间段；第3环混凝土拱顶、拱脚和中间段均再细分成2部分，浇筑顺序为先依次施工拱顶段、中间段和拱脚段第1部分，而后再依次施工拱顶段、拱脚段和中间段第2部分；拱上建筑浇筑顺序为从拱顶向拱脚依次施工。拱架变形和结构应力的实测值与理论值总体上吻合较好，表明该程序与方法合理可靠。

桥梁工程；箱型拱桥；拱架现浇；施工程序

混凝土拱桥结构因性能优越、跨越能力大、耐久性好且外形优美而倍受工程界青睐。拱架法是混凝土拱桥和石拱桥常用的一种施工方法。拱架法施工拱桥的一个难点在于如何合理地划分拱圈混凝土的浇筑长度和浇筑顺序[1]，以控制拱架发生过大变形，防止拱圈混凝土因拱架变形过大而开裂，并减少前期拱圈混凝土所受拉应力。为了保证拱圈混凝土和拱上建筑施工全过程中拱架与拱圈的变形和受力均满足要求，必须先确定合理的浇筑顺序和浇筑长度。

中国多座混凝土拱桥采用了分环分段的拱架施工方法，如：打黑渡怒江大桥[2]、丹河大桥[3]、官地永久交通大桥[4]等。技术人员对拱架现浇混凝土拱圈的分环分段浇筑程序与方法进行了相关研究，蒋云峰等[5]和刘鹏等[6]研究了混凝土现浇时拱架与混凝土的联合作用，周倩等[7]研究了混凝土拱圈的浇筑长度。但以上研究主要以拱架变形为控制要素，未考虑主拱圈浇筑过程中混凝土应力变化所带来的影响。李传习等[8]通过不同施工方案的有限元数值计算与对比研究获得了低扣塔架设钢管混凝土拱桥的合理施工程序与方法。其他国家着重于进行拱桥新工艺及新型组合结构的探索，较少研究拱架现浇拱桥的施工[9-15]。笔者结合甘河沟大桥实际工程，利用Midas/Civil软件对主拱圈纵向浇筑顺序展开研究，对比分析拱圈分环分段施工中每一环拱圈不同的浇筑顺序对拱架变形及先期形成拱圈应力所产生的影响，得出每一环主拱圈浇筑的最优顺序。

1 工程概况

甘河沟大桥位于贵州省毕节市双山新区梨新大道上，跨越甘河沟河谷。甘河沟大桥全长320 m，桥跨布置为3×30 m箱梁+125 m箱型拱桥+3×30 m箱梁，其中，主桥为混凝土箱型拱桥；矢跨比f0/L0=1/5，拱轴系数m=1.756；大桥分为左右两幅，每幅桥面宽23.0 m，设有1.6%纵坡和1.5%横坡。主拱圈拱箱为单箱4室，截面高2.2 m、宽15.6 m。甘河沟大桥采用悬拼钢拱架现浇混凝土的施工方法。甘河沟大桥主桥立面总体布置如图1所示，主拱圈拱箱和钢拱架横向布置如图2所示。

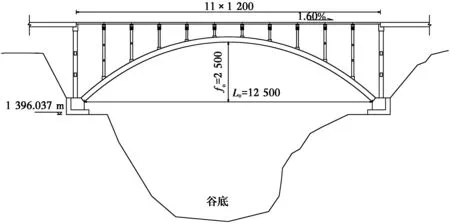
图1 甘河沟大桥主桥立面总体布置图(单位：cm)Fig.1 Schematic diagram of the main bridge of Gan Hegou Bridge (unit:

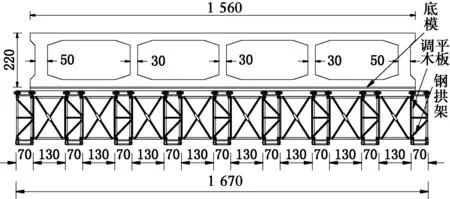
图2 钢拱架横向布置图 (单位:cm)Fig.2 Steel arch horizontal layout (unit:

2 分环分段方案

甘河沟大桥拱圈混凝土浇筑过程按竖向分环、纵向分段的方式进行，并遵循纵向和横向对称、均衡的原则进行施工[16]。按照设计要求，主拱圈竖向共分为3环，第1环为底板和下马蹄部分；第2环为腹板和横隔板部分；第3环为顶板和上马蹄部分，分环位置如图3所示。当第1环混凝土达到90%设计强度后，方可进行第2环混凝土浇筑，第2环混凝土达到90%后方可进行第3环混凝土浇筑。主拱圈纵向分为5段，分段位置分别位于排架2、4、7、9，分段位置如图4所示。

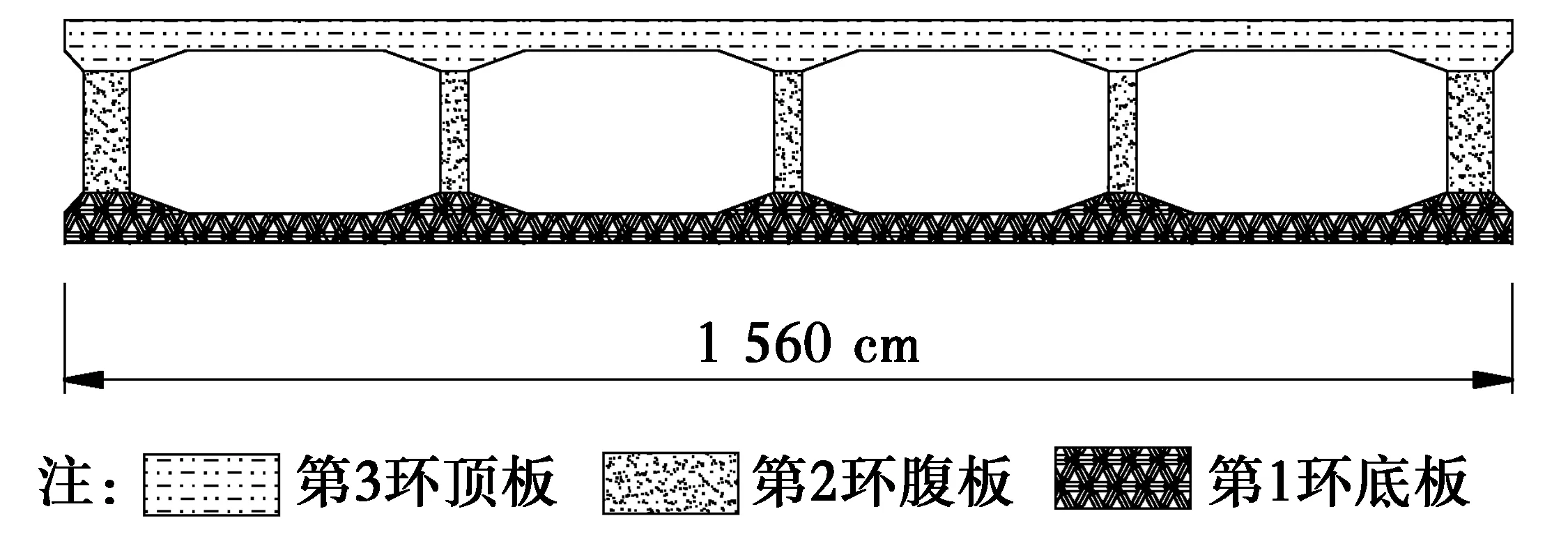
图3 拱圈混凝土分环浇筑示意图Fig.3 Schematic diagram of the arch

钢拱架拱顶截面变形显著，以钢拱架拱顶截面变形为分析对象，通过分析拱架跨中截面的挠度影响线[17]，可以确定混凝土浇筑过程中拱顶挠度的变化。从图5中的拱顶挠度影响线可以看出，因拱脚区段为正挠度区域，拱圈混凝土由拱脚向拱顶浇筑时，浇筑该区域混凝土将使拱架拱顶向上变形。随着混凝土继续浇筑，混凝土进入负挠度区域，拱架拱顶开始向下变形。在混凝土浇筑过程中应使拱顶竖向位置变化和结构应力尽可能小，为此，每一环拱圈混凝土初步拟定了4种可能的浇筑方案，如表1所示，表中字母所表示区段见图4。

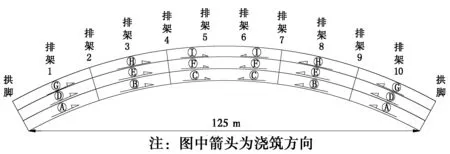
图4 拱圈混凝土分段浇筑示意图Fig.4 Schematic diagram of the arch

图5中，x1、x2分别为沿跨径方向拱圈混凝土浇筑分段点位置；x0为拱顶挠度影响线零点位置；挠度向上为正挠度。

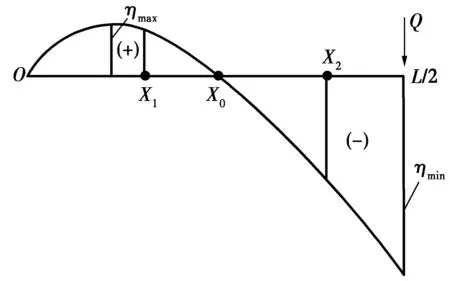
图5 拱顶挠度影响线Fig.

Table 1 Vertical pouring scheme of Concrete arch

环数方案1方案2方案3方案41A→C→BB→A→CB→C→AC→A→B2D→F→EE→D→FE→F→DF→D→E3G→I→HH→G→IH→I→GI→G→H

3 有限元计算模型

采用Midas/Civil软件对甘河沟大桥进行有限元模拟计算，拱圈和拱架的结构离散如图6所示，共有9 246个单元，9 847个节点，3 645个弹性连接。拱架和拱圈均采用梁单元模拟，拱圈底板和拱架之间采用弹性连接中的单向受压单元连接，并释放单元两端弯矩，通过设定受压刚度值来模拟模板受力；底板、腹板、顶板之间采用弹性连接中的刚性选项进行模拟；用释放单元两端弯矩的方式模拟拱架下弦的铰接方式；按两铰拱对钢拱架的边界条件进行约束，按无铰拱对底板、腹板和顶板进行约束。按照上述4种纵向浇筑方案(见表1)分别建立考虑施工全过程的有限元模型。

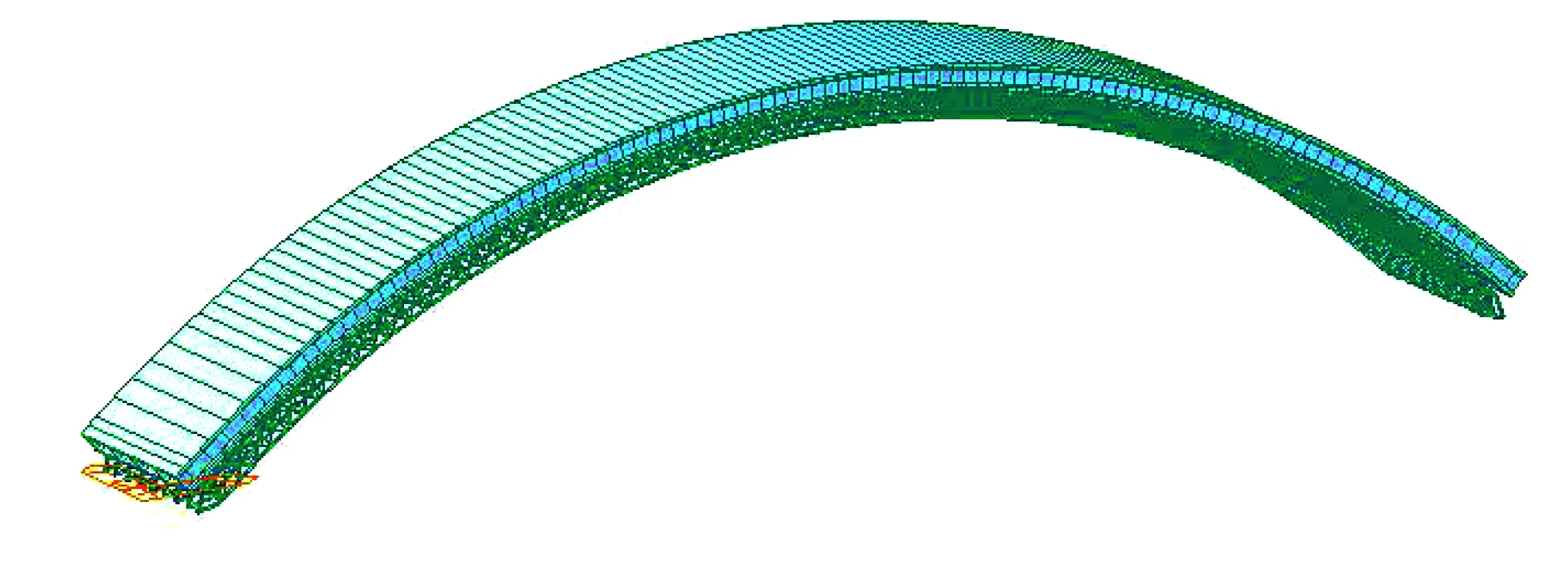
图6 拱架和拱圈的有限元模型单元离散图Fig.6 Element discrete graph of finite element

其中，混凝土的强度随时间增长，考虑混凝土强度的增长对混凝土结构的计算分析非常重要[18]，尤其对采用分环分段施工的桥梁而言。此外，有限元模型也基于以下假设：施工过程中拱圈与拱架不发生相对滑移。

在无试验数据的情况下，采用CEB-FIP规范计算混凝土的弹性模量，混凝土弹性模量随时间变化的计算式为

(1)

Eci=Eco[fcm/fcmo]1/3

(2)

且：Eco=2.15×104MPa，fcmo=10 MPa。

(3)

式中：βcc(t)是强度发展速度，s是水泥种类常数。

甘河沟大桥主桥拱圈全部采用C50的混凝土，fcm=50 MPa，水泥采用的是普通硅酸盐水泥，s取0.25。

4 有限元结果分析

4.1 第1环混凝土浇筑

第1环混凝土浇筑过程中，由于混凝土尚未凝固，强度和刚度都很小，无法承担自重，其重量将全部由拱架承担。因此，在浇筑第1环混凝土过程中主要考查钢拱架变形，根据建立的有限元模型对4种不同浇筑方案进行对比分析，其结果如图7所示。

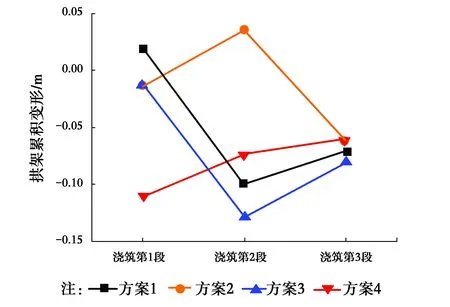
图7 第1环混凝土不同浇筑顺序对拱架拱顶变形的影响Fig.7 The effect of the first ring concrete pouring in

从图7可以看出，在4种方案中，方案1和方案2的拱架拱顶变形相对较小。方案2首先浇筑中间段混凝土，由于拱脚段坡度较大，混凝土容易流向拱脚位置，不利于实际施工。方案1首先浇筑拱脚段混凝土，有利于施工。因此，可确定采用方案1进行第1环混凝土的浇筑。

4.2 第2环混凝土浇筑

在浇筑第2环混凝土时，第1环混凝土已经达到设计强度的90%以上，可以和拱架一起共同承担第2环混凝土的重量，即此时的承重结构为拱架和第1环混凝土。在浇筑第2环混凝土的过程中不仅要分析拱架的变形还要考虑第1环混凝土的应力大小，以防混凝土开裂。第2环混凝土不同浇筑方案的拱架拱顶变形和结构应力结果如图8和表2所示。

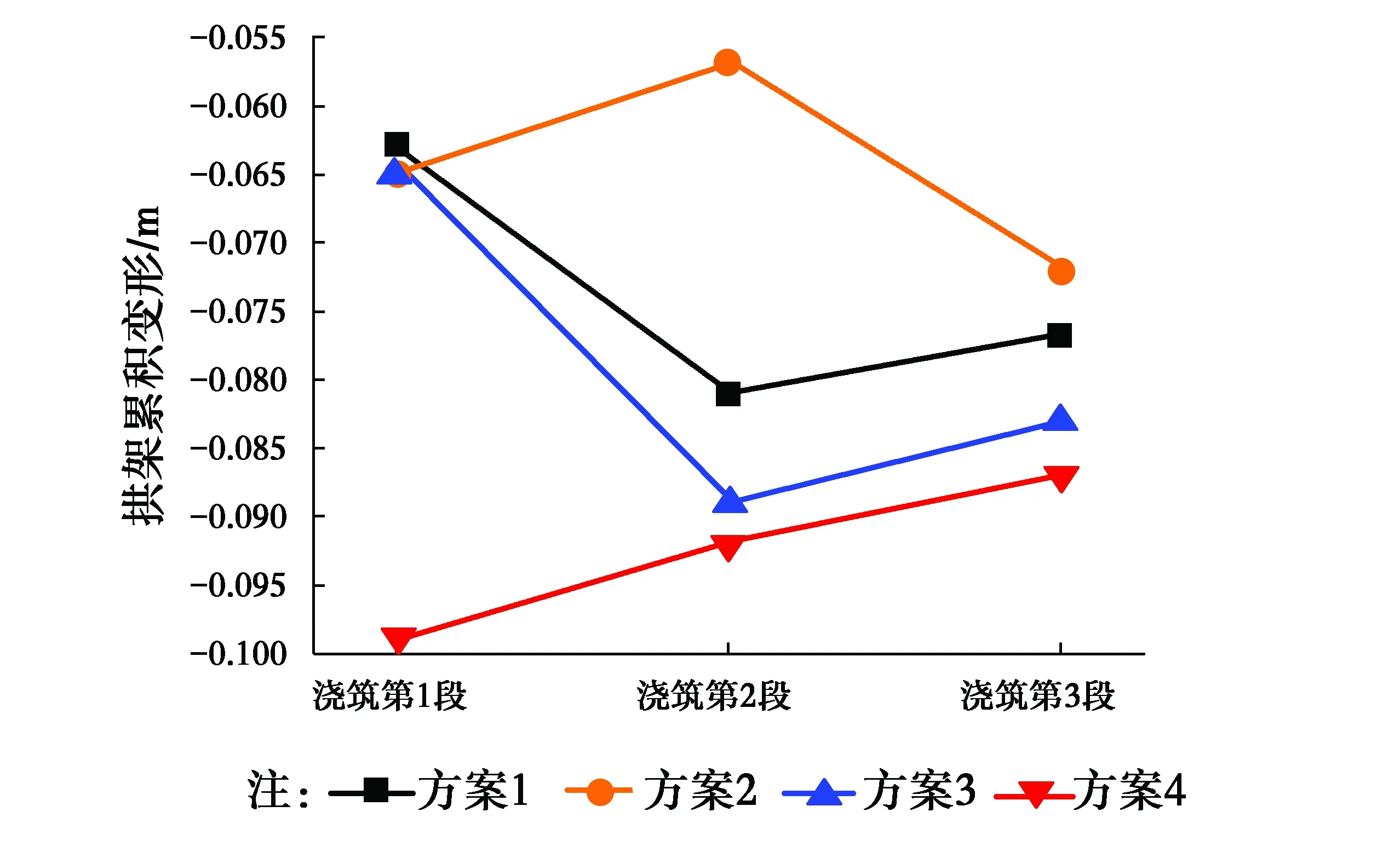
图8 第2环混凝土不同浇筑顺序对拱架拱顶变形的影响Fig.8 The effect of the second ring concrete pouring in

Table 2 Contrast of extreme adverse stress on slabs in arch

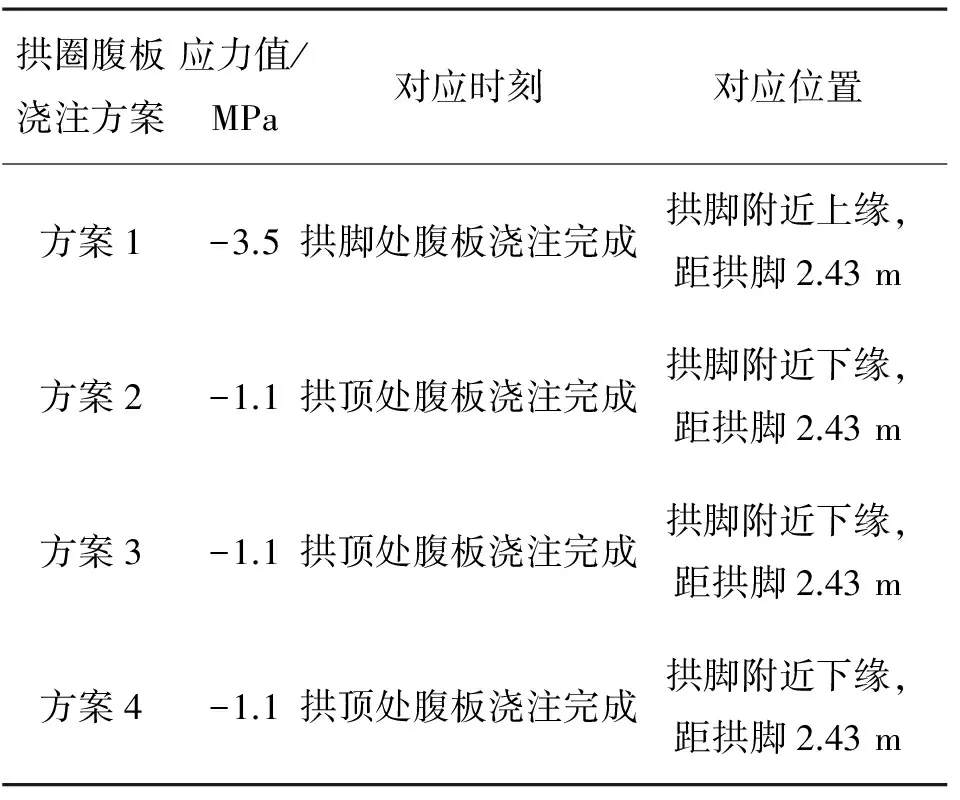
拱圈腹板浇注方案应力值/MPa对应时刻对应位置方案1-3．5拱脚处腹板浇注完成拱脚附近上缘，距拱脚2．43m方案2-1．1拱顶处腹板浇注完成拱脚附近下缘，距拱脚2．43m方案3-1．1拱顶处腹板浇注完成拱脚附近下缘，距拱脚2．43m方案4-1．1拱顶处腹板浇注完成拱脚附近下缘，距拱脚2．43m

注：拉应力为负，以下同。

由图8和表2可看出第2环混凝土不同施工方案下的拱架变形和第1环混凝土应力大小。方案1虽然拱架变形不大，但是其前期形成的混凝土拉应力较大，其值达到了-3.5 MPa，相对而言，其他浇筑方案拉应力大小均为-1.1 MPa，减少了68%。综合考虑拱架变形、第1环混凝土拉应力大小和施工方便，采用方案4进行第2环混凝土的浇筑。

4.3 第3环混凝土浇筑

在浇筑第3环混凝土时，第2环混凝土已经达到设计强度的90%以上，可以和第1环混凝土以及拱架一起共同承担第3环混凝土的重量，即此时的承重结构为拱架和第1、2环混凝土。在浇筑第3环混凝土过程中同样需考虑拱架变形和前期形成拱圈的应力。第3环混凝土不同浇筑方案的拱架拱顶变形和结构应力结果如图9和表3所示。

由图9和表3可看出第3环混凝土不同施工方案下的拱架变形和第2环混凝土应力大小。方案1虽然拱架变形不大，但是其前期形成的混凝土拉应力最大，达到了-5.4 MPa，而方案4拉应力最小为-1.7 MPa。为进一步减少拱圈的拉应力，降低拱圈混凝土开裂风险，增加第3环混凝土浇筑的分段数如图10所示，并对其浇筑顺序进行了研究，拱圈腹板应力结果如表4所示。

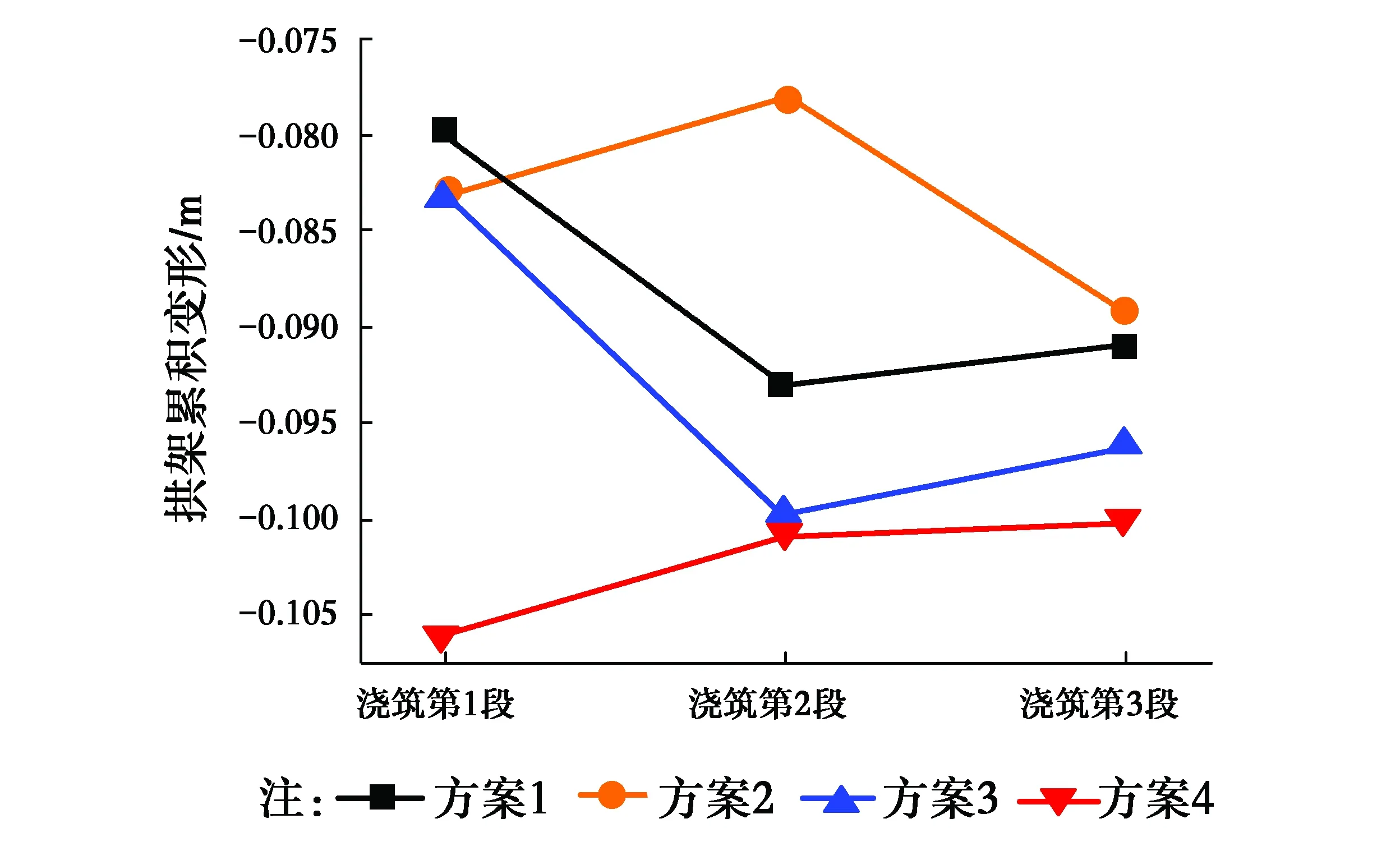
图9 第3环混凝土不同浇筑顺序对拱架拱顶变形的影响Fig.9 The effect of the third loop concrete casting in different

Table 3 Contrast of extreme adverse stress on slabs in arch web

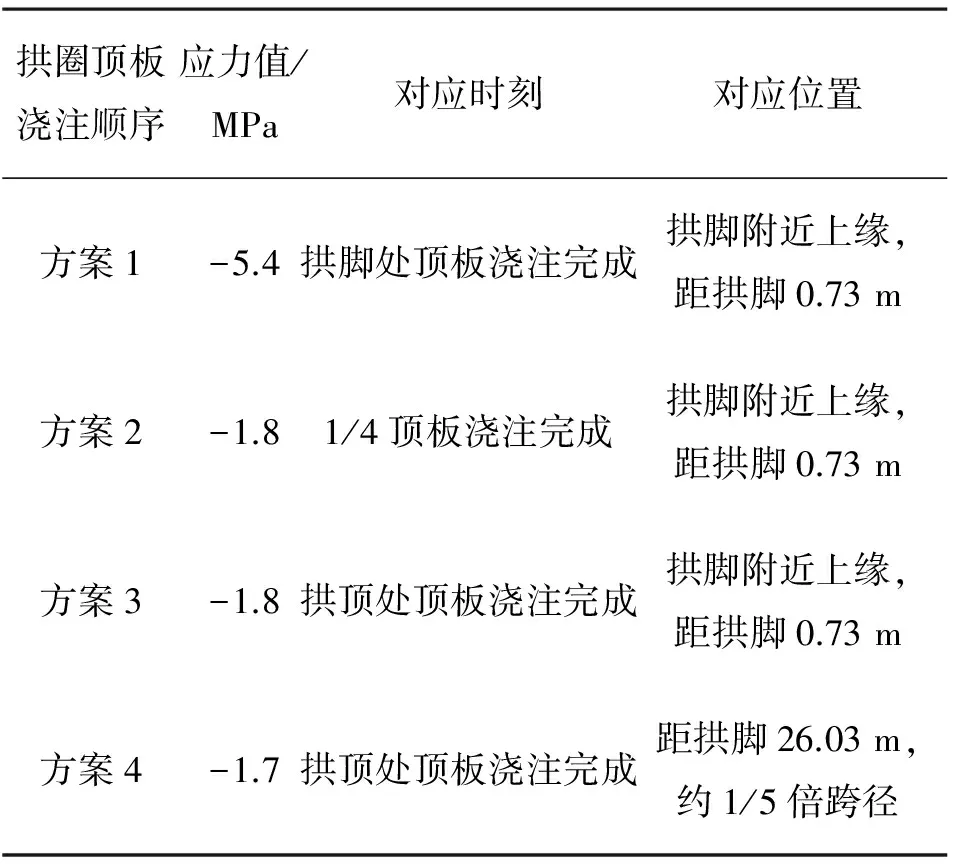
拱圈顶板浇注顺序应力值/MPa对应时刻对应位置方案1-5．4拱脚处顶板浇注完成拱脚附近上缘，距拱脚0．73m方案2-1．81/4顶板浇注完成拱脚附近上缘，距拱脚0．73m方案3-1．8拱顶处顶板浇注完成拱脚附近上缘，距拱脚0．73m方案4-1．7拱顶处顶板浇注完成距拱脚26．03m，约1/5倍跨径

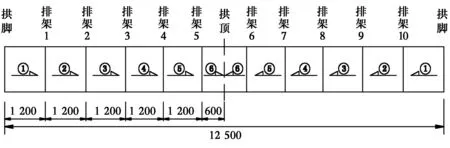
图10 第3环混凝土浇筑节段平面图(单位：cm)Fig.10 The plane graph of the third loop concrete casting (Unit:

Table 4 Contrast of extreme adverse stresson slabs in arch web

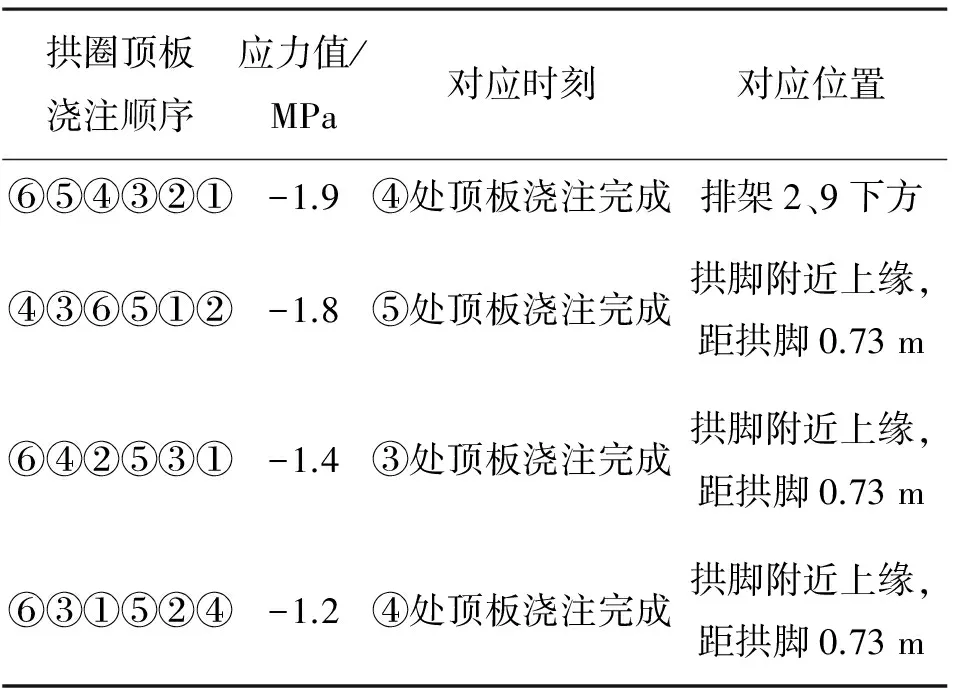
拱圈顶板浇注顺序应力值/MPa对应时刻对应位置⑥⑤④③②①-1．9④处顶板浇注完成排架2、9下方④③⑥⑤①②-1．8⑤处顶板浇注完成拱脚附近上缘，距拱脚0．73m⑥④②⑤③①-1．4③处顶板浇注完成拱脚附近上缘，距拱脚0．73m⑥③①⑤②④-1．2④处顶板浇注完成拱脚附近上缘，距拱脚0．73m

注：⑥⑤④③②①表示先浇筑图10中⑥所分区段，再依次浇筑⑤、④、③、②、①所标注区段，以此类推。

从表4可见，较为合理顺序为⑥③①⑤②④，最不利应力出现在所有拱圈顶板混凝土浇注完成时，位置为拱脚附近，数值为1.2 MPa。

4.4 拱上建筑施工

拱上排架及空心板的施工顺序也会对主拱圈受力产生一定影响，为了减小拱圈的拉应力，对拱上排架和空心板的施工顺序进行对比分析，其结果如表5所示。由表5可知，当拱上排架及空心板由拱顶向拱脚浇筑时，拱圈顶板的拉应力最小。

表5 拱圈顶板不利应力极值对比

Table 5 Contrast of extreme adverse stress on slabs in arch roof

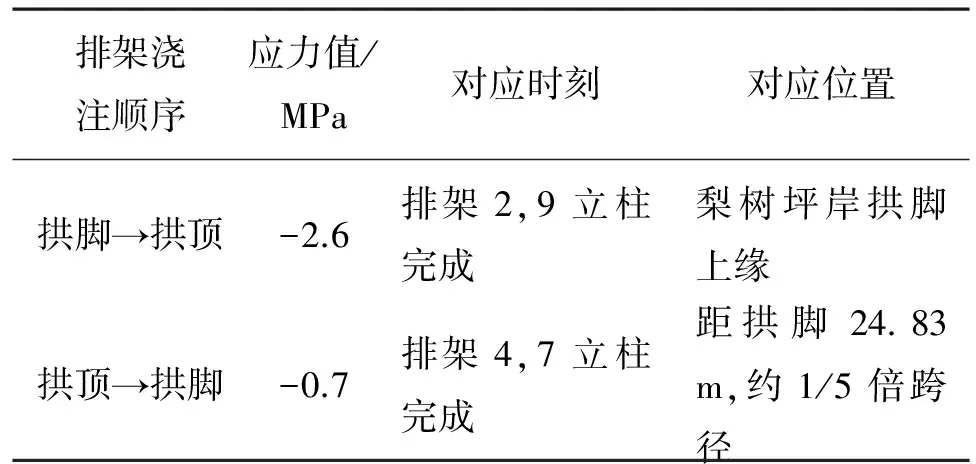
排架浇注顺序应力值/MPa对应时刻对应位置拱脚→拱顶-2．6排架2，9立柱完成梨树坪岸拱脚上缘拱顶→拱脚-0．7排架4，7立柱完成距拱脚24．83m，约1/5倍跨径

注:拉应力为负。

4.5 温度作用影响分析

桥涵设计中通常将温度作用分成均匀温度和梯度温度两种进行考虑，均匀温度变化相对较简单且早已被结构设计所考虑，而非线性的梯度温度相对较复杂且往往是设计计算的控制因素。目前，日照竖向温度梯度的确定主要是依据《公路桥涵设计通用规范》，钢筋混凝土箱形拱桥在施工过程中受到日照温度的影响，其截面应力将会产生变化，为了研究日照梯度温度对结构应力作用的大小，计算规范规定的梯度温度作用下[19]结构的最大应力，其结果如图11所示。由图11可知，在主拱圈浇筑过程中，由于日照温度作用产生的每一环拱圈混凝土最大拉、压应力相差不大，其中最大拉应力为0.79 MPa，最大压应力为1.80 MPa，温度应力对结构造成的影响不容忽视，主拱圈结构应该选取在凌晨温度变化最小的时段进行合拢浇筑。

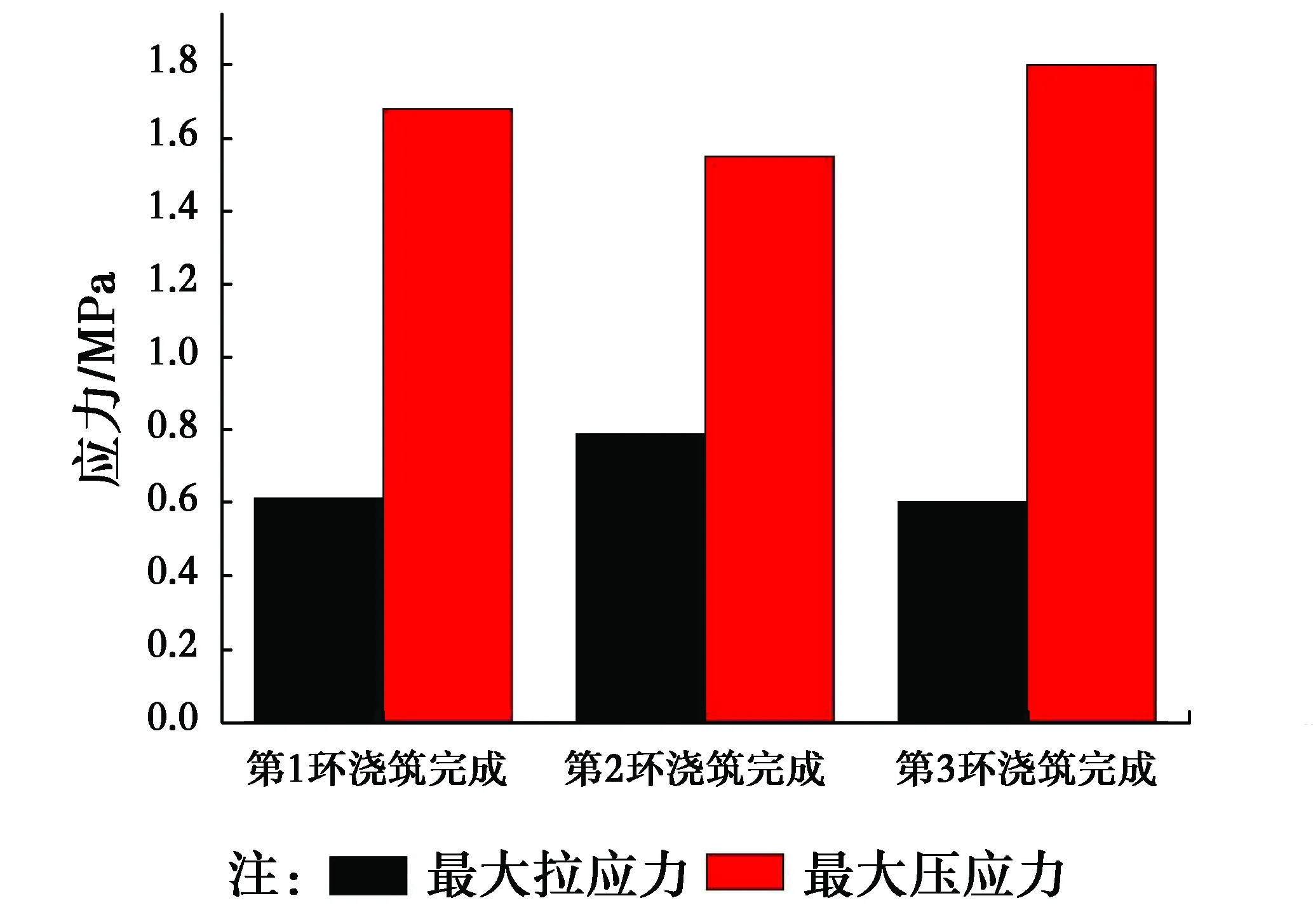
图11 主拱圈浇筑过程截面梯度温度最大温度应力值Fig.11 The maximum values of temperature stress by

5 主拱圈浇筑过程实测数据分析

在每一环混凝土浇筑完成后采用全站仪对钢拱架产生变形进行实测，将实测值与理论值比较，如图11～13所示；在第2环和第3环混凝土浇筑完成后采用施工过程中预埋的振弦式应变计对底板混凝土相应位置的应力进行实测，将实测值与理论值比较，如图14～15所示。从图11～15中可得出，拱架拱顶变形和底板应力大部分测点的实测值与理论值总体趋势和走向一致(个别测点由于测试和计算误差的存在，有一定的差别)，表明了上述有限元计算与所确定的程序与方法的可靠性。

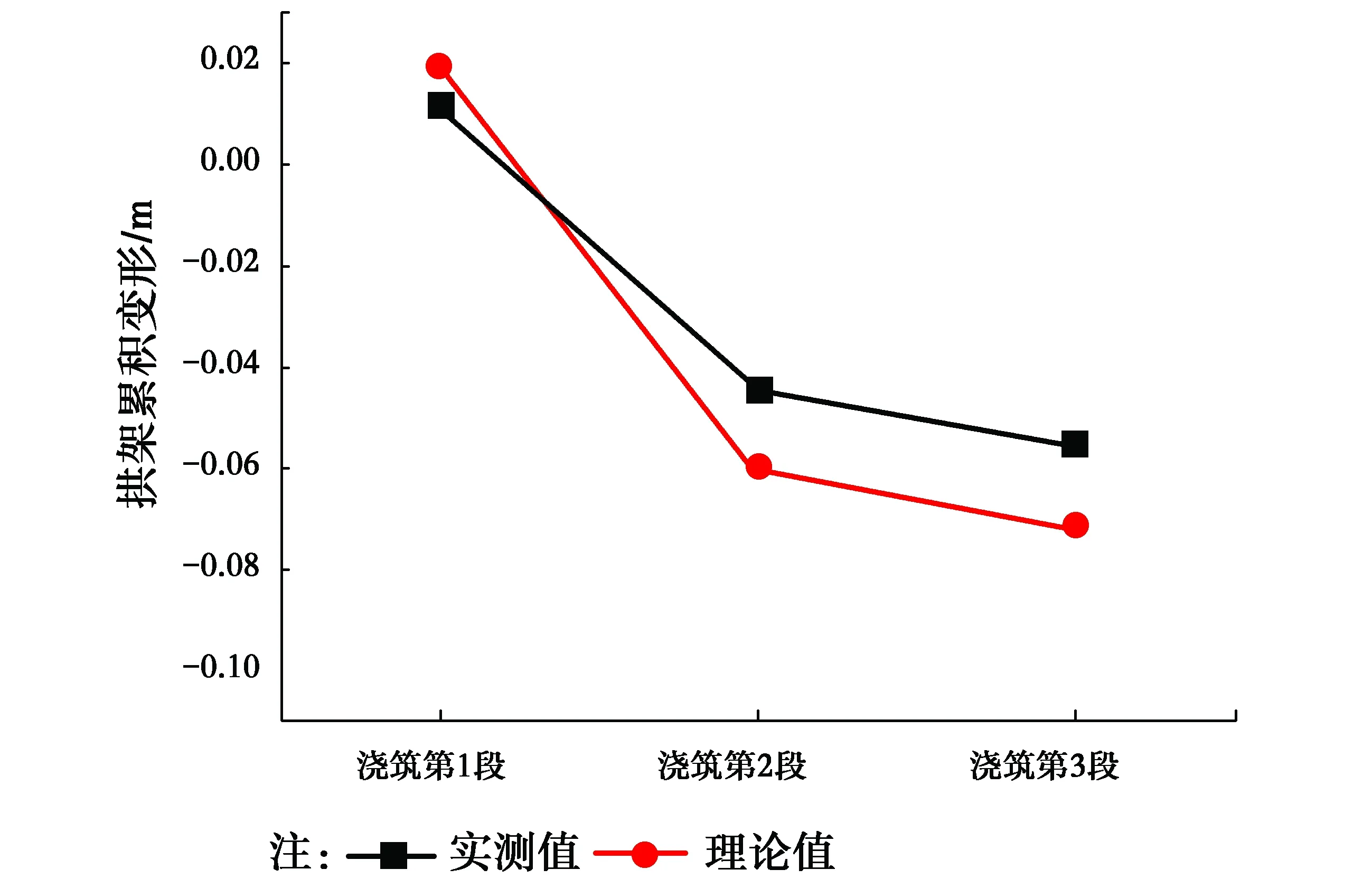
图12 第1环混凝土浇筑拱架拱顶变形实测值与理论值对比Fig.12 The comparison between measured value and theoretical

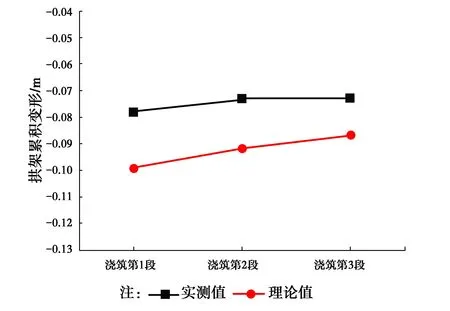
图13 第2环混凝土浇筑拱架拱顶变形实测值与理论值对比Fig.13 The comparison between measured value and theoretical value of arch deformation on the second ring concrete pouring

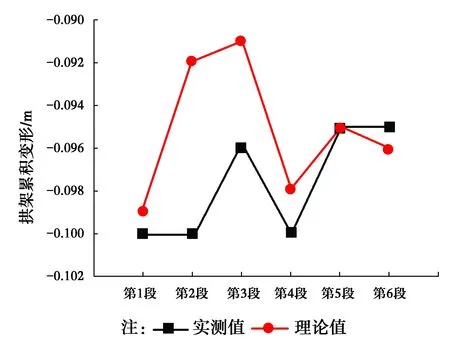
图14 第3环混凝土浇筑拱架变形实测值与理论值对比Fig.14 The comparison between measured value and theoretical value of arch deformation on the third ring concrete pouring

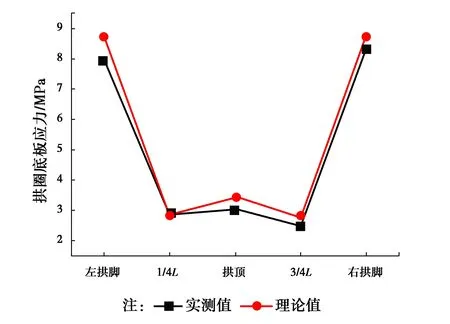
图15 第2环混凝土浇筑后底板应力实测值与理论值对比Fig.15 The comparison between measured value and theoretical value of floor stress after

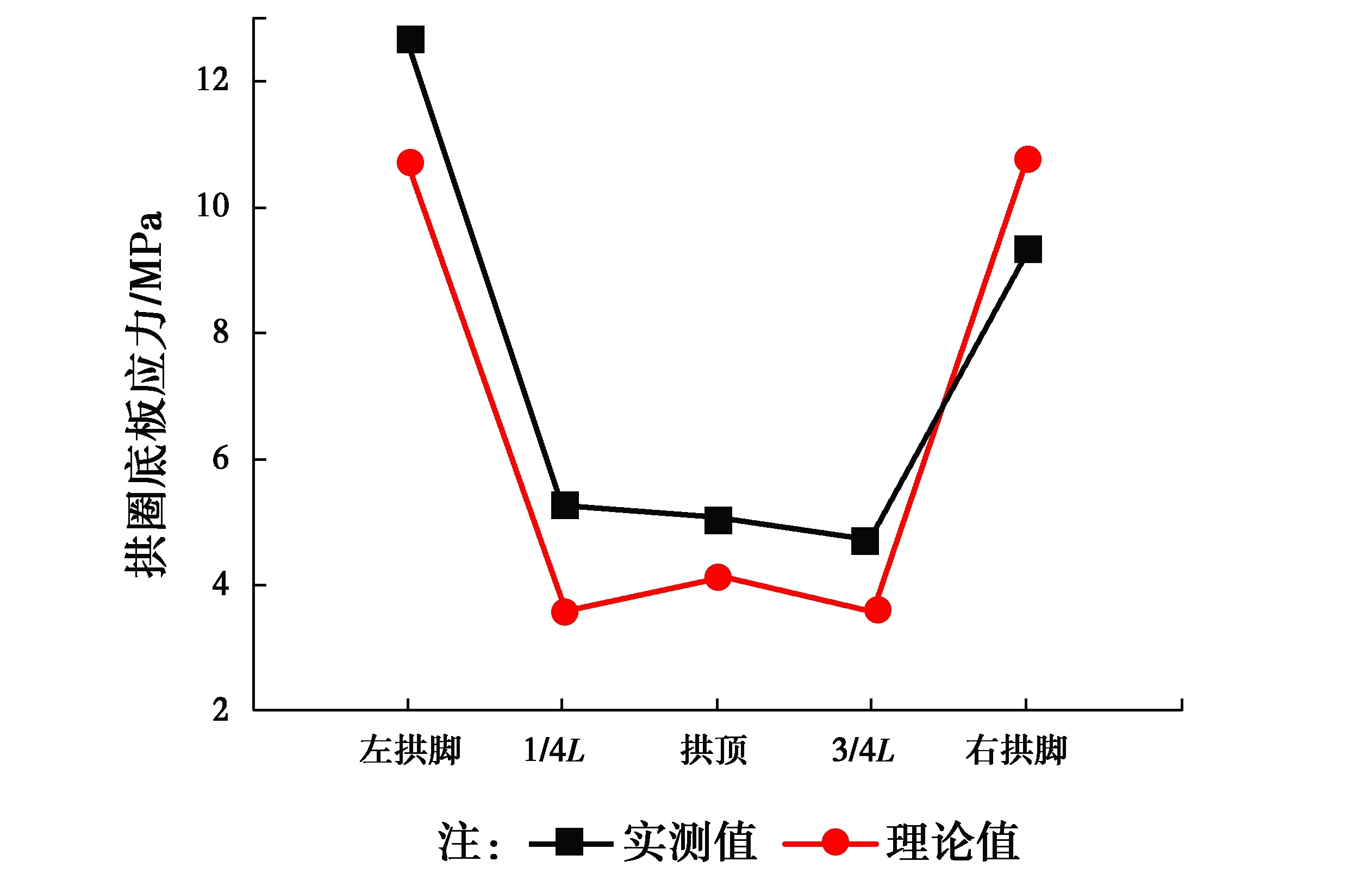
图16 第3环混凝土浇筑后底板应力实测值与理论值对比Fig.16 The comparison between measured value and theoretical

6 结论

采用Midas/Civil有限元软件建立计算模型，对甘河沟大桥主桥相同分环方法、不同分段浇筑顺序的混凝土拱圈受力及拱架变形分别进行模拟和对比分析，确定了合理施工程序与方法，可得到如下结论:

1)拱圈第1环混凝土的施工只需考虑钢拱架变形的影响，最优的浇筑顺序为：拱脚段→拱顶段→中间段。

2)拱圈第2环和第3环混凝土的施工需综合考虑钢拱架变形及前期成形拱圈混凝土应力的影响，第2环混凝土浇筑顺序为：拱顶段→拱脚段→中间段；第3环混凝土浇筑顺序为：拱顶段1→中间段1→拱脚段1→拱顶段2→拱脚段2→中间段2。

3)选择合理的拱上排架及空心板施工顺序能有效减少拱圈拉应力，降低混凝土裂缝出现的风险，拱上建筑最优浇筑顺序为：拱顶→拱脚。

4)拱圈施工过程中拱架变形及底板应力的实测值与理论值总体上吻合较好，表明所确定的施工程序与方法合理可靠。

[1] 朱懿. 钢筋混凝土拱桥拱架现浇施工技术研究[D].重庆: 重庆交通大学, 2012. ZHU Y. Study on the cast-in-place construction technology of reinforced concrete arch bridge [D]. Chongqing: Chongqing Jiaotong University, 2012. (in Chinese)

[2] 吴高峰, 徐鸿. 打黑渡怒江大桥拱架及拱肋施工过程计算 [J]. 建筑钢结构进展, 2005, 7(1): 47-50. WU G F, XU H. Construction calculation of arch bracket and arch rib in Daheidu Nujiang Bridge [J]. Progress in Steel Building Structures, 2005, 7(1): 47-50. (in Chinese)

[3] 胡崇武, 范立础. 丹河大桥拱圈与拱架共同作用研究[J]. 公路, 2005(4): 50-53. HU C W, FAN L C. Research on coaction of arch ring and arch centering of Danhe River Bridge [J]. Highway, 2005(4): 50-53. (in Chinese)

[4] 刘鹏. 利用MSC.Marc模拟现浇钢筋混凝土箱形拱桥施工方法[J]. 西部交通科技, 2008(3): 47-49. LIU P. The simulated construction method for casting-in-place reinforced concrete box arch bridge by means of MSC.Marc [J]. Western China Communications Science & Technology, 2008(3): 47-49. (in Chinese)

[5] 蒋云锋, 陈思甜, 龚尚龙, 等. 钢筋混凝土箱形拱桥现浇施工拱圈-拱架联合受力仿真分析[J]. 黑龙江科技信息, 2009(4): 211. JIANG Y F, CHEN S T, GONG S L, et al. Reinforced concrete box arch bridge construction of cast-in-situ arch ring-arch bridge with a combined bearing simulation analysis [J]. Heilongjiang Science and Technology Information, 2009(4): 211. (in Chinese)

[6] 刘鹏, 陈思甜, 郑凯锋. 分环现浇混凝土拱圈与拱架联合作用机理[J]. 公路, 2011(3): 14-19. LIU P, CHEN S T, ZHENG K F. Co-action mechanism of concrete cast-in-situ box arch ring and arch centering [J]. Highway, 2011(3): 14-19. (in Chinese)

[7] 周倩, 周水兴, 刘勇. 基于变形指标控制混凝土拱桥拱架现浇分段长度研究[J]. 华东公路, 2012(5): 11-13. ZHOU Q, ZHOU S X, LIU Y. Deformation control of cast-in-place concrete arch bridge arch index based on segment length [J]. East China Highway, 2012(5): 11-13. (in Chinese)

[8] 李传习, 左雁, 董创文. 低扣塔架设钢管混凝土拱桥的合理施工程序与方法[C]//中国土木工程学会桥梁及结构工程分会. 第二十届全国桥梁学术会议论文集(上册), 2012: 7. LI C X, ZUO Y, DONG C W. Reasonable construction procedure and method of the concrete filled steel tube arch bridge with low pylon [C]//Bridge and Structural Engineering Branch of China Civil Engineering Society. The Twentieth National Bridge Academic Conference Proceedings(I), 2012: 7. (in Chinese)

[10] KRISTEK V, FOGLAR M. Centre-line optimisation of buried arch bridges [J]. Proceedings of the Institution of Civil Engineers-Bridge Engineering, 2012, 165(3): 159-168.

[11] ELLIS B, ELLIS B J J. New concrete arch bridge at Victoria Avenue, Lincoln, Canada [J]. Proceedings of the Institution of Civil Engineers-Bridge Engineering, 2012, 165(3): 195-197.

[12] GRANATA M F, MARGIOTTA P, RECUPERO A, et al. Concrete arch bridges built by lattice cantilevers [J]. Structural Engineering & Mechanics, 2013, 45(5): 703-722.

[13] GOU H Y, PU Q H, WANG J M, et al. Spatial mechanical behaviors of long-span V-shape rigid frame composite arch bridges [J]. Structural Engineering and Mechanics, 2013, 47(1):59-73.

[14] BI K M, HAO H, REN W X, et al. Seismic response of a concrete filled steel tubular arch bridge to spatially varying ground motions including local site effect [J]. Advances in Structural Engineering, 2013, 16(10): 1799-1818.

[15] AHMED E A, SETTECASI F, BENMOKRANE B, et al. Construction and testing of GFRP steel hybrid-reinforced concrete bridge-deck slabs of sainte-catherine overpass bridges [J]. Journal of Bridge Engineering, 2014,19(6):213-226.

[16] 秦豹. 混凝土拱桥箱型截面现浇拱圈分环施工方式研究[D]. 武汉: 武汉理工大学, 2010. QIN B. Research on layering construction cast-in-place concrete arch bridge with box section [D]. Wuhan: Wuhan University of Technology, 2010. (in Chinese)

[17] 周水兴, 邓翔. 拱架现浇钢筋混凝土拱圈浇筑长度研究[J]. 重庆交通大学学报(自然科版), 2013, 32 (4): 569-572, 620. ZHOU S X, DENG X. Casting length of cast-in-place RC arch rib in arch centering [J]. Journal of Chongqing Jiaotong University (Natural Sciences), 2013, 32 (4): 569-572, 620. (in Chinese)

[18] GRIDER A, RAMIREZ J A, YUN Y M. Structural Concrete Design [M]//Structural Engineering Handbook, Boca Raton: CRC Press LLC, 1999.

[19] 公路桥涵设计通用规范:JTG D 60—2004 [S]. 北京:人民交通出版社, 2004: 88-89. General code for design of highway bridges and culverts: JTG D 60-2004 [S]. Beijing: China Communications Press, 2004: 88-89. (in Chinese)

(编辑 胡英奎)

Reasonable construction procedure and method of the cast-in-place RC arch rib with arch centering

ZhangYuping,PengBihui,LiChuanxi,DongChuangwen

(School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410114, P. R. China)

At present， the arch deformation is considered mainly when the engineers determinate the construction procedure for the cast-in-place RC arch with arch centering, but the arch stress is often ignored. Gan Hegou Bridge in Guizhou province is select as the case study. The positions of dividing rings sections are defined preliminarily according to original construction scheme. The simulation analysis considering the whole construction process is done by the use of MIDAS software. After the arch deformation and arch stress of various schemes are calculated and compared, reasonable construction procedure is obtained. The pouring sequence of the first arch ring is the first springer, the second vault and the last middle section. The pouring sequence of the second arch ring is the first vault, the second springer and the last middle section. The springer、vault and middle section of the third arch ring are divided into the two sections. The pouring sequence of the third arch ring are the first section of the vault、springer and middle section, then the section of the vault、springer and middle section. The pouring sequence of spandrel construction is the first vault, the second springer. The measured values of the arch deformation and stress are agreement with the calculated values. The results show the procedure and method are reasonable and reliable.

bridge engineering; box arch bridge; cast-in-place arch; construction procedure

2016-04-13

国家重点基础研究发展计划(973项目)(2015CB057702)；国家自然科学基金(51378080)；长沙理工大学土木工程优势特色重点学科创新性项目(15ZDXK02)

张玉平(1976-)，男，博士，副教授，主要从事从事桥梁施工控制和桥梁结构分析理论研究, (E-mail)zyp5032@163.com。

Foundation item：Key Basic Research Development Program of China (973 Program)(No.2015CB057702)；National Natural Science Foundation of China (No.51378080)；Changsha University of Science and Technology Advantage and Characteristic Civil Engineering Key Subjects (No.15ZDXK02)

10.11835/j.issn.1674-4764.2016.06.011

U448.22

A

1674-4764(2016)06-0083-08

Received:2016-04-13

Author brief：Zhang Yuping(1976-), PhD, associate professor, main research interests: bridge construction control and bridge structure analysis, ( E-mail)zyp5032@163.com.