输电钢管塔空间KK型管板连接节点极限承载力

刘堃，李正良，尤军，涂胤

(1.重庆大学 土木工程学院，重庆 400045；2.中国煤炭科工集团 重庆设计研究院，重庆 400039)



输电钢管塔空间KK型管板连接节点极限承载力

刘堃1，李正良1，尤军2，涂胤1

(1.重庆大学 土木工程学院，重庆 400045；2.中国煤炭科工集团 重庆设计研究院，重庆 400039)

空间KK型管板连接节点作为输电钢管塔中最主要的节点型式，其安全性是整个塔架结构安全的重要保证。相比较于平面K型节点，在考虑实际结构中节点空间效应后的KK型节点的受力性能更为复杂。在平面K型管板节点的试验研究基础上，对两类空间KK型管板节点展开参数化分析，重点讨论了节点几何尺寸参数和主管轴压应力比等因素对节点极限承载力的影响变化规律。结合大量有限元参数分析所得计算结果，并综合考虑各种因素对节点极限承载力的影响，提出了空间KK型管板连接节点在主管管壁局部屈曲破坏模式下的极限承载力建议计算方法。

输电钢管塔；空间KK型；管板连接节点；极限承载力

近年来，中国的电网建设快速发展，输电线路的输送容量和电压等级不断提高，杆塔承受的荷载也越来越大，传统的角钢塔已不能满足发展的需要。钢管塔因具有风压小、刚度大、结构简洁、传力清晰等众多优点，在大跨越工程和特高压输电线路中得到广泛应用。输电钢管塔属于高耸的空间桁架结构，各钢管构件是由节点相互连接在一起的，杆件的传力完全通过节点来实现。因此，节点设计及其构造处理的好坏将直接影响到钢管塔整体受力性能。节点破坏后会带来一系列连锁效应，导致从局部到整体的连续破坏，因此，安全可靠性对整个塔架而言至关重要[1]。

目前，在输电钢管塔节点的构造连接方面普遍采用管板连接方式，但对此类节点受力性能的研究还很少，缺乏相应的设计理论用于指导工程实践。更为重要的是，以往所进行的研究主要是针对平面K型管板节点，对于空间KK型节点的研究非常少[2-5]。因实际输电钢管塔结构中的该类管板节点不是平面K型，而是空间KK型的，在考虑实际节点的空间效应(包括：几何空间效应和荷载空间效应)后，其受力情况和破坏模式更为复杂[6]。通常情况下空间KK型管板节点呈现以下3种破坏模态：1)主管管壁钢材受力下局部超出弹性阶段产生塑性变形而破坏；2)节点板过早破坏导致节点丧失承载力的局部失效破坏；3)上述两种情况并存下的破坏模式。但截止到目前为止，相关规范[7-9]还没有专门方法来计算这类节点的承载力。本文依托实际工程，研究在第一类破坏模式下输电塔空间KK型节点的极限承载力。

1 K型管板连接节点承载力试验研究

1.1 试验样本

以现工程常见的K型管板节点承载力试验为基础展开后续讨论，试验如图1所示。主管和支管的尺寸分别为φ219×6和φ133×6，K型节点中承压支管和受拉支管与主管夹角分别为45°和50°，主管长2 m，其中：在节点板与主管相交的上下端部位置设置了1/4环形加强板。各节点试件所用材料均为Q345钢，具体尺寸参数如表1所示。

表1 试验样本

Table 1 The experimental specifications

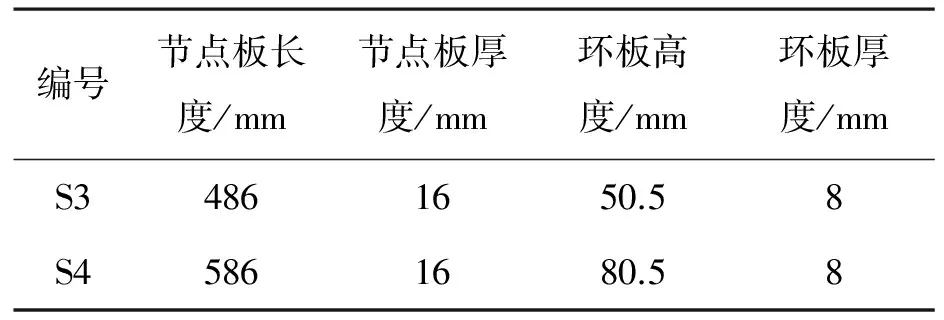
编号节点板长度/mm节点板厚度/mm环板高度/mm环板厚度/mmS34861650．58S45861680．58

1.2 试验装置和加载方案

试验装置如图1所示，应变片布置如图2所示。主管底部与三角形钢支座铰接，主管上部及各支管的端部用千斤顶连接。

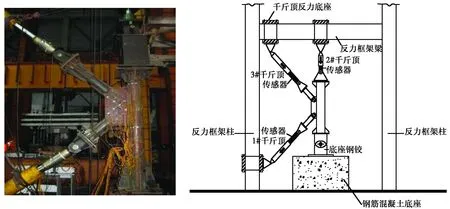
图1 节点试验装置Fig.1 The test device of the joint

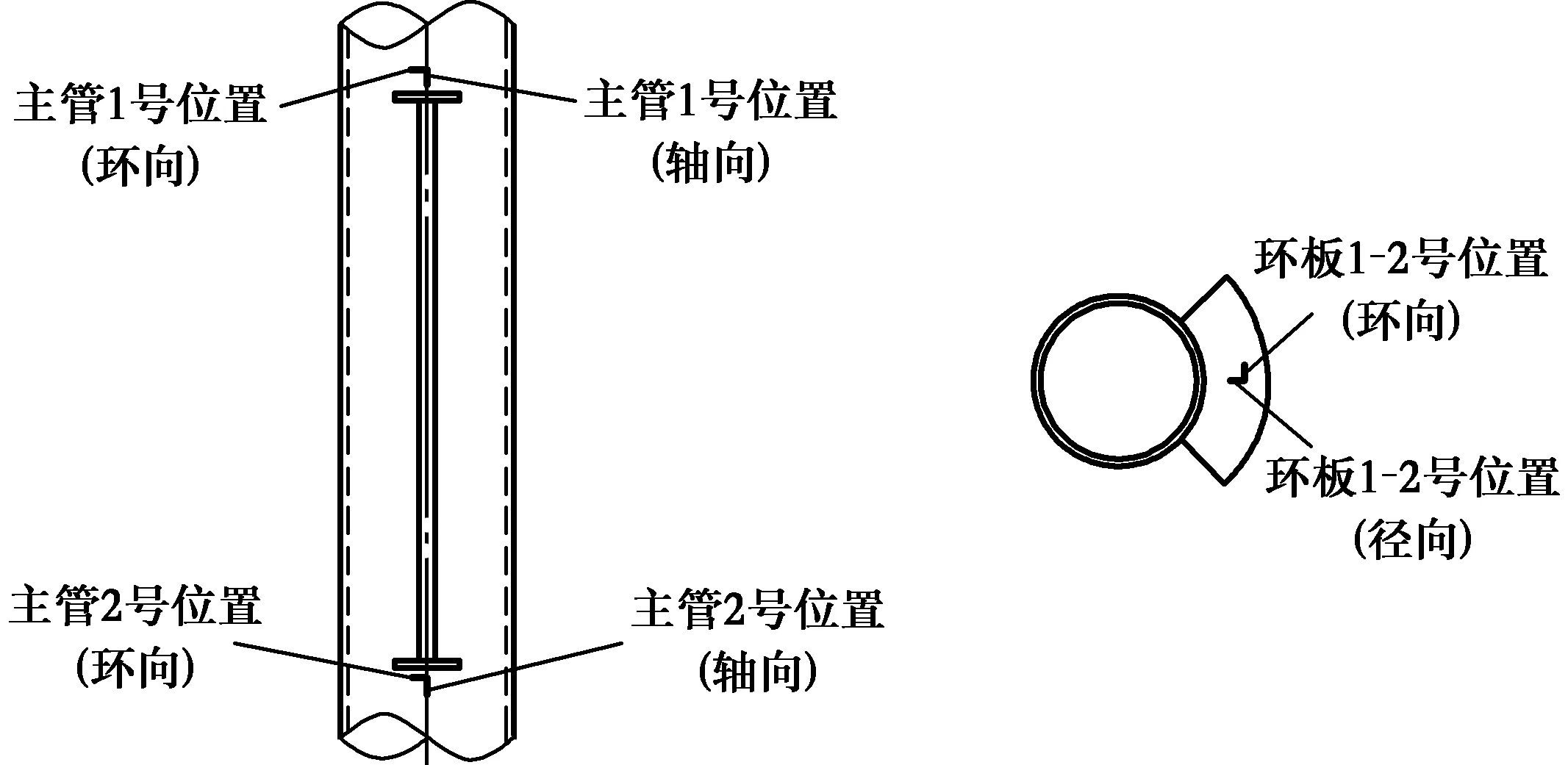
图2 关键测点应变片布置Fig.

加载采用分级加载，每级加载后停顿1 min，再继续加载。具体加载方式为：与主管上端连接的2#千斤顶施加轴压力，与上支管端部连接的3#千斤顶施加轴压力，与下支管端部连接的1#千斤顶施加轴拉力，主管与支管同步加载，当主管轴压力达到0.2Pv,y时，停止对主管加载，此时支管仍继续加载，直至发生破坏。

1.3 试验结果

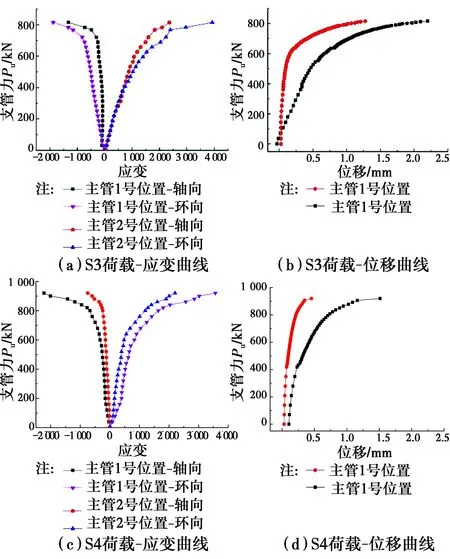
图4 试件S3 和S4荷载变形曲线Fig.4 The load-displacement response

应变的变化随荷载逐渐增大呈现先直线后曲线的趋势，非线性变化是判断屈服的标准。当荷载继续增加，节点的塑性区进一步扩展，最终在主管与环板附近的塑性区域形成贯通，节点达到极限承载力状态。随着主管与支管上所施加荷载的不断增加，下端环板附近的主管区域首先进入屈服阶段。荷载继续增大，此区域发生塑性变形后内力重新分布，且扩大影响范围至节点局部明显变形而破坏。在整个加载过程中，环板、节点板、支管和插板等均未达到其极限承载力，没有发生破坏。

从节点试件的破坏变形图中可以看出，节点试件的主管均在其管壁上的1号关键点处出现了局部凹陷，在2号关键点处出现了局部凸起，且2号点处的变形量较1号点处明显。但由于环板的加强作用，这两点处的变形量均较小；当节点达到极限承载力时，在受拉支管一侧的主管管壁与环板的相交处甚至出现了拉裂现象。

2 管板连接节点有限元分析模型验证

采用ANSYS中的SHELL181单元建立节点有限元模型，模型的材料属性、边界条件和加载方式等均与试验相同。

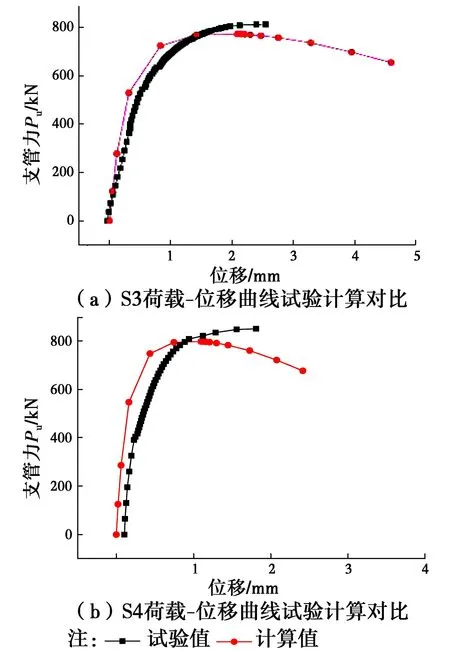
图5 节点荷载位移曲线Fig.5 The load-

3 空间KK型管板节点极限承载力参数分析

对于空间KK型管板节点，其几何参数如图6所示，按有无偏心分别对以下两类节点的极限承载力展开有限元参数分析：无偏心全环板节点和负偏心全环板节点。节点极限承载力主要受主管直径D和管壁厚度t、节点板高度B和环板高度R、环板厚度tr和节点板之间的夹角β，支管偏心大小e/D等影响。主管与环板为Q345钢，屈服强度fy=345 MPa，弹性模量Es=2.06×105N/mm2，泊松比μ=0.3。ANSYS中采用Von-Mises屈服准则定义材料弹塑性的发展，基于等向强化理论的流动法则定义单元刚度。

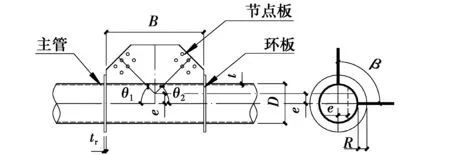
图6 KK型节点几何参数示意图Fig.6 Schematic diagram of KK-

3.1 无偏心全环板KK型节点

针对带全环板的空间KK型管板节点[10-15]的极限承载力展开研究分析，节点有限元模型网格划分如图7所示。

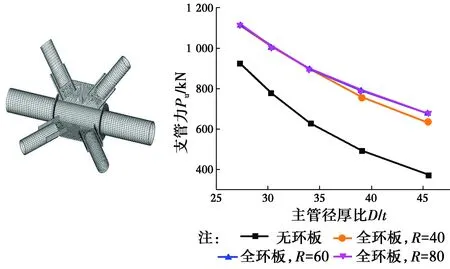
图7 全环板KK型节点计算模型Fig.7 Finite element model of KK-

对于无偏心全环板空间KK型管板连接节点各影响参数的取值如表2所示，并根据这些计算参数，设计了多组节点，进行有限元参数分析。

表2 无偏心全环板KK型节点计算参数表

Table. 2 The calculation parameters of KK-joints with annular ribbed plate

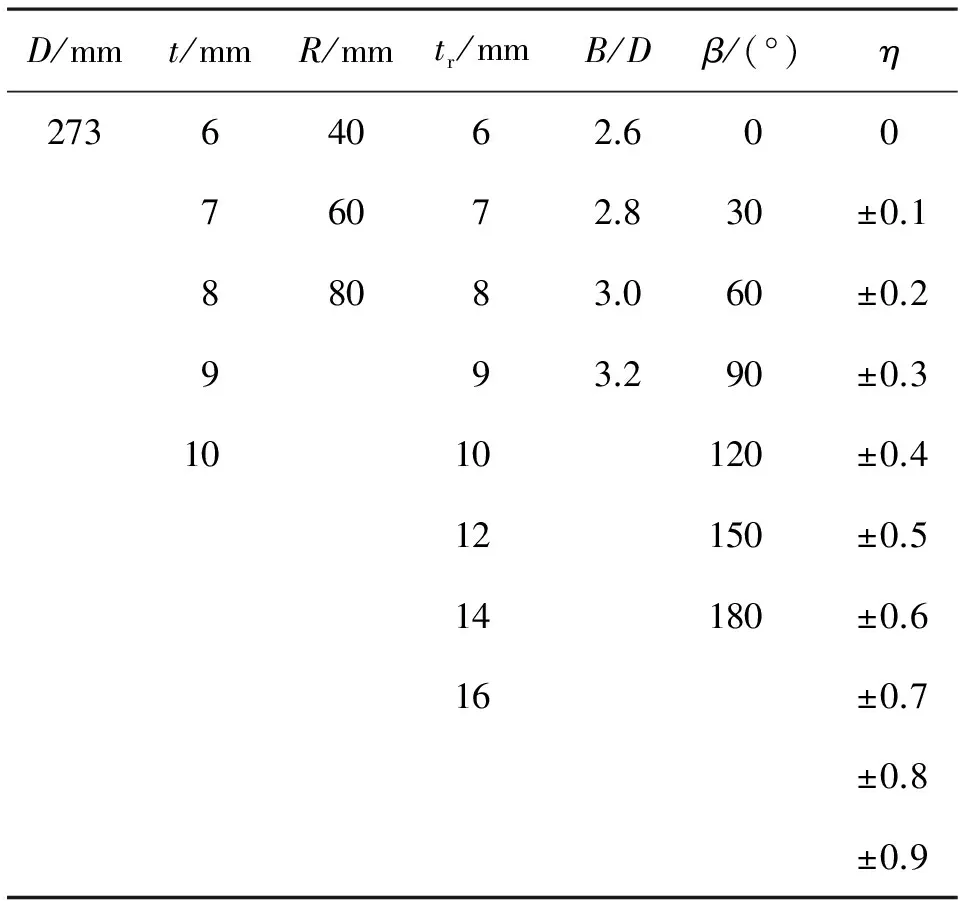
D/mmt/mmR/mmtr/mmB/Dβ/(°)η27364062．60076072．830±0．188083．060±0．2993．290±0．31010120±0．412150±0．514180±0．616±0．7±0．8±0．9

3.1.1 夹角β对节点极限承载力的影响 选取主管直径D=273 mm，节点板高度B=709.8 mm(其他尺寸根据表2进行无量纲化组合)的全环板空间KK型管板节点，讨论夹角β对承载力的影响，结果如图8所示。

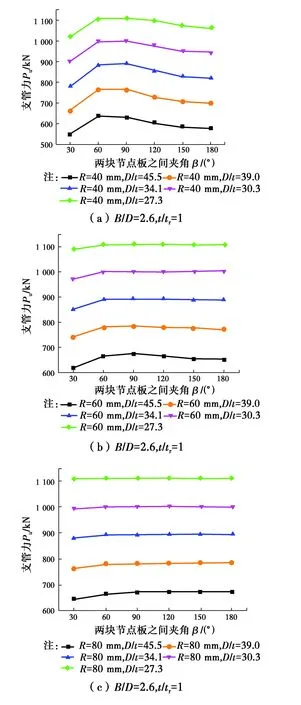
图8 夹角β对全环板KK型节点极限承载力的影响Fig.8 The influence of β on the ultimate strength of KK-

从图中可以看出，当环板高度较小，R=40 mm时，夹角β的变化对节点承载力的影响较明显，这时节点的破坏主要是由环板的局部屈服控制或主管与环板联合控制。当环板高度增加，R=60 mm时，夹角β的变化对节点承载力的影响开始表现得不再明显，此时除β=30°时的节点承载力稍小外，β在60°～180°之间变化时，节点的承载力基本保持不变。当环板高度较高，R=80 mm时，与R=60 mm的情况基本相同，节点的破坏由主管控制，不同夹角β情况下各节点的极限承载力基本相同。

3.1.2 主管径厚比D/t对节点极限承载力的影响 选取主管直径D=273 mm，节点板高度B=709.8 mm，环板高度R=60 mm，主管管壁厚度t=6 mm，环板厚度tr=6 mm的全环板空间KK型管板节点，讨论D/t对承载力的影响，计算结果如图9所示。

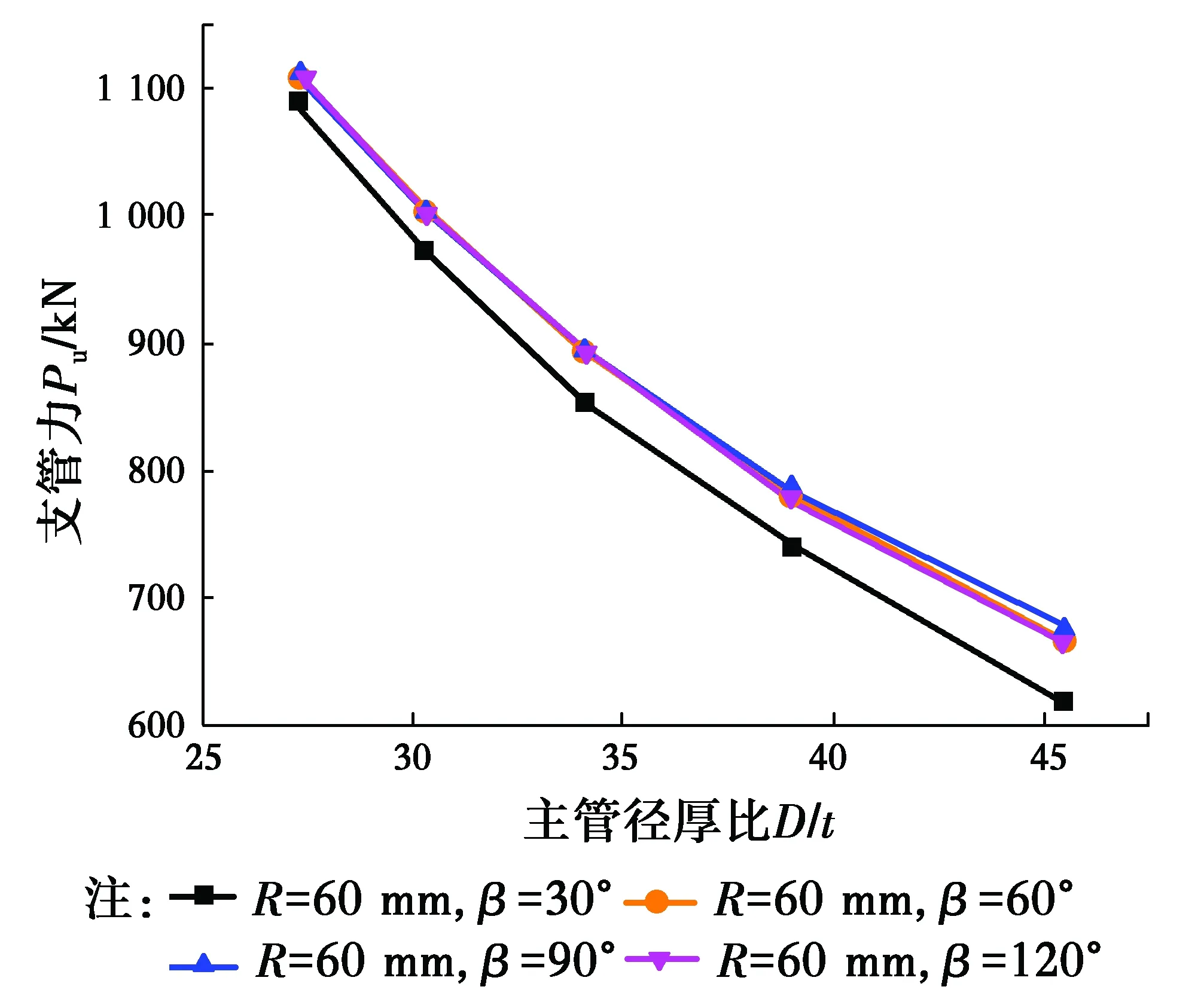
图9 D/t对全环板KK型节点极限承载力的影响Fig.9 The influence of D/t on the ultimate strength of KK-

结果表明，节点极限承载力Pu值与D/t呈现指数规律的逆相关，随D/t的增大而减小。

3.1.3 节点板高度与主管直径比B/D对极限承载力的影响 主管直径D=273 mm，主管管壁厚度t=6 mm，环板厚度tr=6 mm的全环板空间KK型管板节点，分别讨论在不同的R和夹角β情况下，节点的极限承载力随节点板高度与主管直径之比B/D的变化规律，计算结果如图11所示。

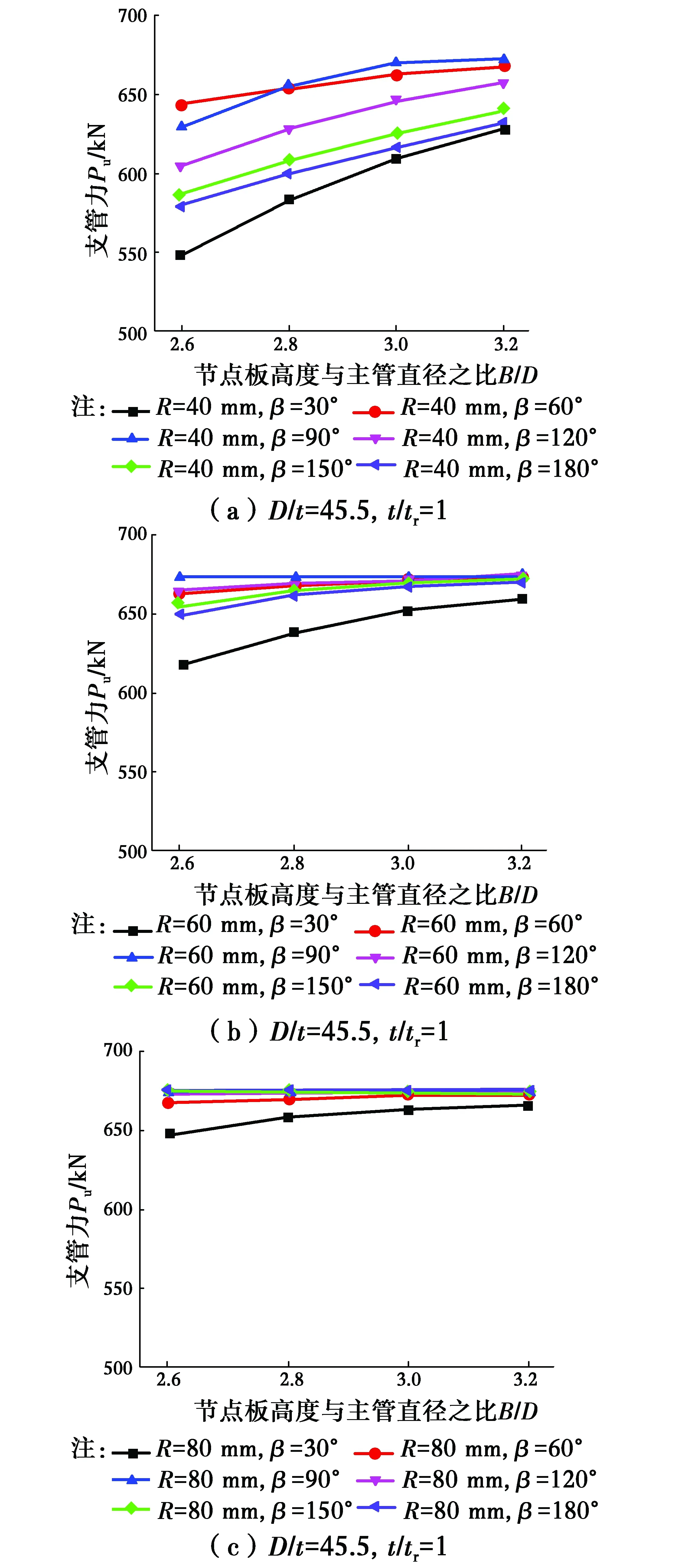
图10 B/D对全环板KK型节点极限承载力的影响Fig.10 The influence of B/D on the ultimate strength of KK-

从图10可以看出，对于全环板KK型节点，节点板高度的增加对节点承载力的提高作用很小，这是因为在增加全环板后，节点的承载力不再由节点板与主管相交处主管管壁局部塑性变形控制，而由节点板、下端全环板在主管管壁上相交区域的塑性变形控制，与节点板高度关系不大，过高的节点板不能得到有效利用，因此，工程设计中节点板高度按构造取值即可。

3.1.4 节点主管直径与环板高度比D/R对极限承载力的影响 选取主管直径D=273 mm，管壁厚度t=8 mm，环板厚度tr=6 mm的全环板空间KK型管板节点，讨论节点的极限承载力随D/R的变化规律，计算结果如图11所示。

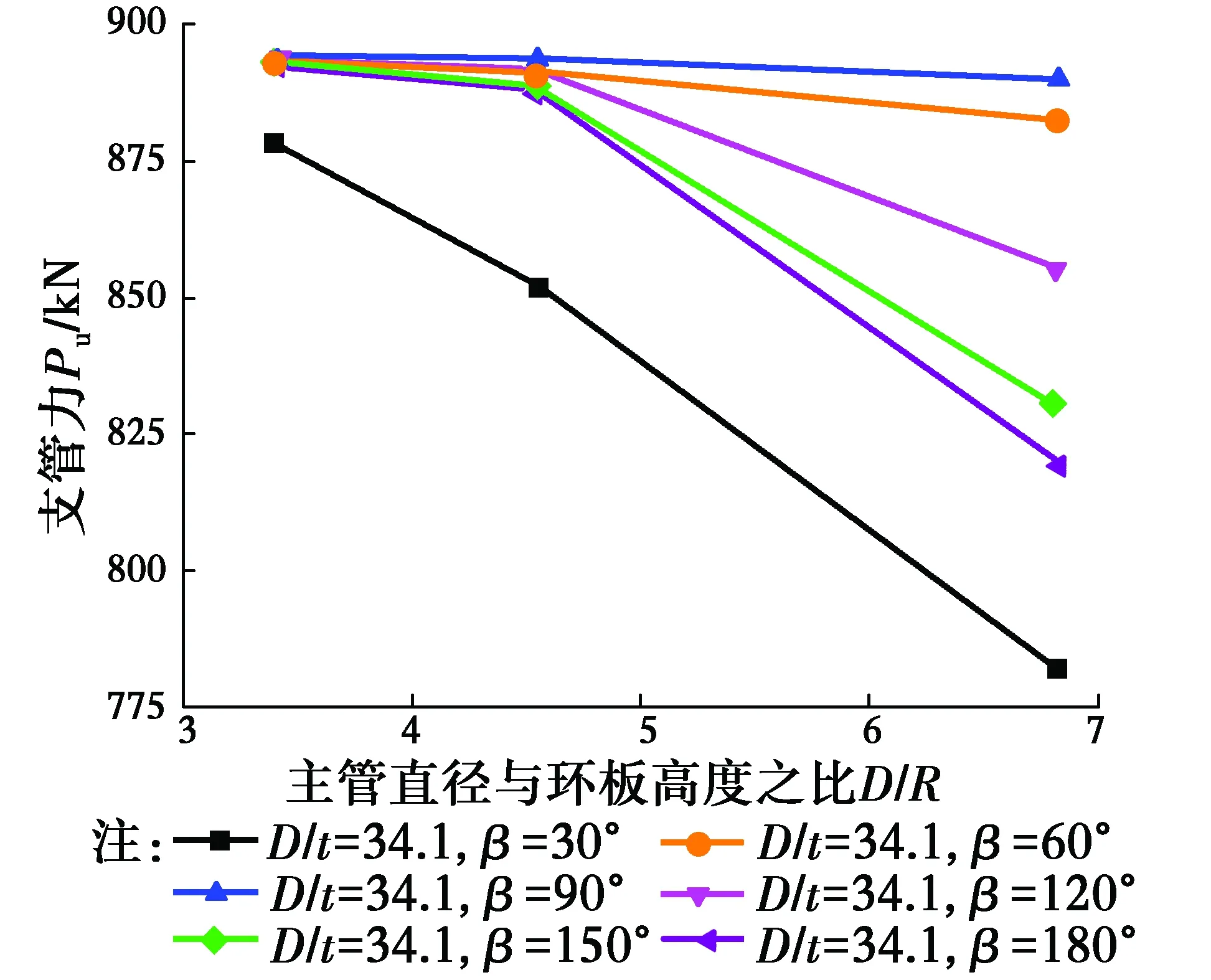
图11 D/R对全环板KK型节点极限承载力的影响Fig.11 The influence of D/R on the ultimate strength of KK-

从图中可以看出，环板高度的增加对节点承载力的提高作用存在一个有效范围，当R从40 mm增加到60 mm时，对节点承载力的提高作用较为明显，而当R从60 mm增加到80 mm时，节点承载力增幅很小。这是因为R较小时，节点的破坏模式由环板控制，节点达到极限承载力时，环板先于主管发生破坏；而R较大时，节点的破坏模式由主管控制。在工程设计中，对于全环板高度的取值应根据主管直径D和壁厚t来确定，同时考虑节点设计的相关构造要求，将R控制在一个有效合理的范围内。

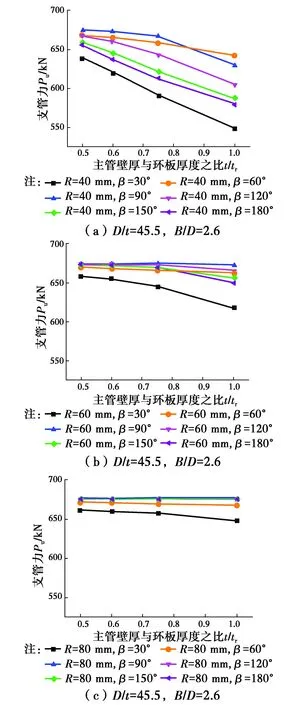
图12 t/tr对全环板KK型节点极限承载力的影响Fig.12 The influence of t/tr on the ultimate strength of KK-

3.1.5 主管管壁厚度与环板厚度之比t/tr对节点极限承载力的影响 选取主管直径D=273 mm，节点板高度B=709.8 mm，主管管壁厚度t=6 mm的全环板KK型节点，讨论在不同的R和夹角β情况下节点的极限承载力随t/tr的变化规律，计算结果如图12所示。从图中可以看出，t/tr对节点承载力的影响与环板高度R取值有较大关系。当环板高度较小，R=40 mm时，节点承载力由环板控制，t/tr的变化对节点的承载力存在较大影响，节点的承载力与t/tr变化规律呈现逆相关。随着环板高度的增加，当R=60或80 mm时，节点的破坏模式转变为由主管控制，此时环板厚度的增加对节点极限承载力的提高作用很小。

3.1.6 主管的轴向应力比η对节点极限承载力的影响 选取D=273 mm、t=8 mm、B=710 mm、R=60 mm、tr=8 mm的管板节点，讨论平面K型节点和空间KK型节点(β=90°)分别在主管受轴拉或轴压作用时，节点承载力的变化情况，计算结果如图13所示。

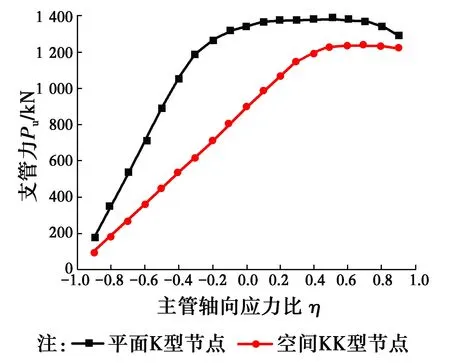
图13 η对全环板K型与KK型节点极限承载力的影响Fig.13 The influence of η on the ultimate strength of K-joint and KK-joint both with annular ribbed plate

从图13可以看出，主管受压时，η绝对值越大，K型节点和KK型节点承载力越小。主管受拉时，随着η的增大，节点的承载力有一定程度提高，但拉力过大时，节点的承载力出现下降。主管轴向拉应力比η从0增加到0.9，K型节点的极限承载力的最大增幅仅为2.72%，基本可忽略不计。但KK型节点的极限承载力则有明显增加，增幅达到38.1%，这是因为空间KK型节点在增加全环板后，节点的主管、节点板和全环板共同形成了一个紧密的空间受力整体，在主管受轴向拉力时，不仅有主管参与，而且节点板和全环板也参与了受力，所以，全环板空间KK型节点在主管受轴拉作用时，节点承载力的提高较明显。下面着重讨论在不同的D/t、B/D、t/tr、R和夹角β情况下主管受压时，其轴压应力比η对节点极限承载力的影响，计算结果如图14所示。

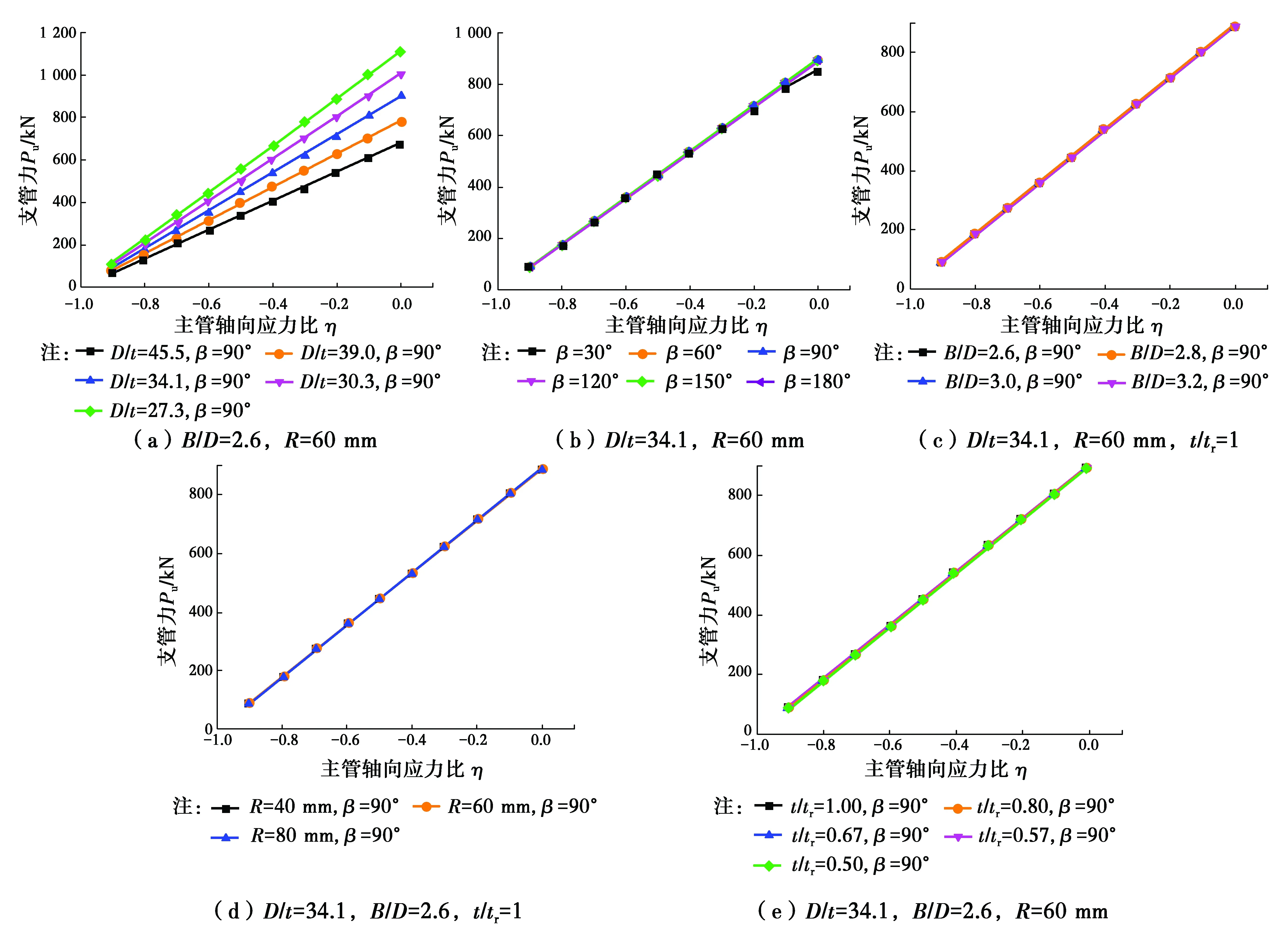
图14 η对全环板KK型节点极限承载力的影响Fig.14 The influence of η on the ultimate strength of KK-

从图14可以看出，在各种不同情况下，当主管轴压应力比η从0增加到0.9的过程中，全环板KK型节点的承载力均出现了明显下降，在输电塔设计中必须考虑主管轴向压力对承载力的影响。

3.2 负偏心全环板KK型节点

前面对无偏心全环板KK型节点的承载力进行了研究。相较于这类节点，负偏心全环板KK型节点的受力性能更为复杂，其极限承载力与无偏心全环板KK型节点存在较大差别。本节将针对负偏心全环板KK型节点的承载力展开讨论。对于负偏心全环板空间KK型管板连接节点各几何参数的取值如下表3所示，并根据这些计算参数，设计了多组节点，进行有限元参数分析。

表3 负偏心全环板KK型节点计算参数表

Table.3 The calculation parameters of KK-joints with eccentricity and annular ribbed plate

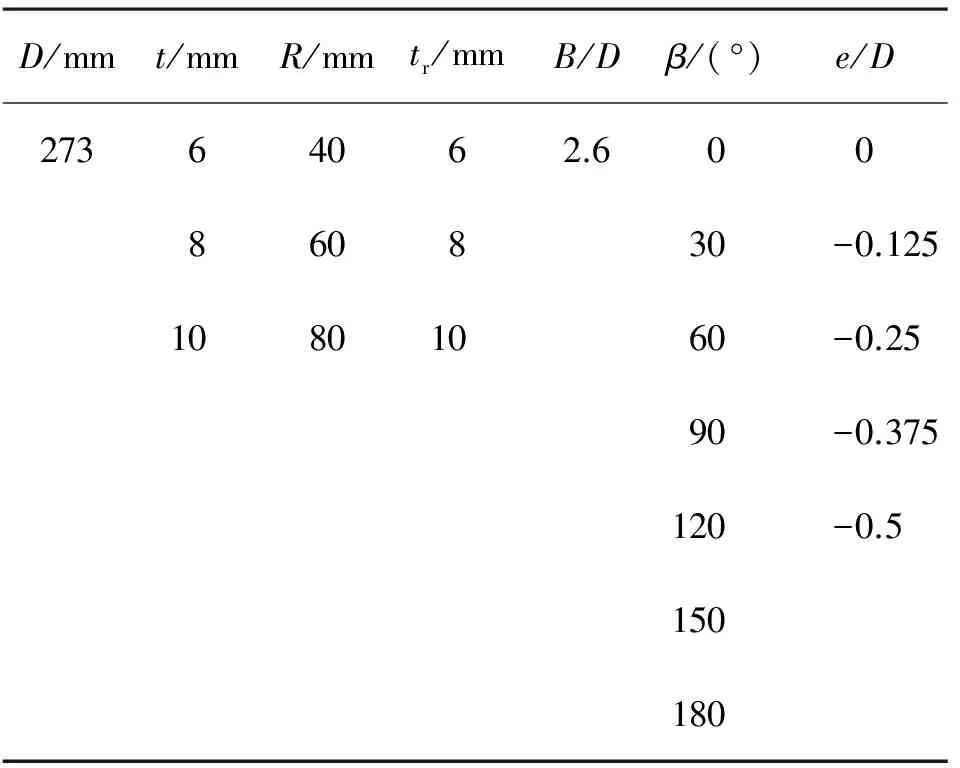
D/mmt/mmR/mmtr/mmB/Dβ/(°)e/D27364062．600860830-0．12510801060-0．2590-0．375120-0．5150180

3.2.1 平面K型节点与空间KK型节点极限承载力对比 选取主管直径D=273 mm，节点板高度B=709.8 mm，主管管壁厚度t=6 mm，环板厚度tr=6 mm的管板节点，讨论负偏心全环板空间KK型节点(β=90°)与负偏心全环板平面K型节点极限承载力的差异，计算结果如图15所示。

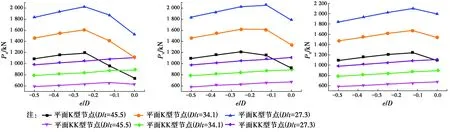
图15 负偏心全环板K型与KK型节点极限承载力对比Fig.15 The comparison of ultimate strength between K-joints and KK-

从图15可以看出，对于负偏心情况下带全环板的K型节点与KK型节点之间的承载力存在较大差异。平面K型节点的承载力随e/D的增加，先增大后逐渐降低；而负偏心全环板KK型节点的承载力，在e=0增加到e=-D/2的整个过程中，节点的极限承载力一直呈下降趋势。由此可见，对于带全环板的空间KK型管板节点，支管的负偏心连接并不一定是有利的。3.2.2 支管偏心大小e/D对节点的极限承载力的影响 本节研究不同D/t、R和夹角β下，支管的偏心大小e/D对全环板空间KK型节点的极限承载力的影响，其中Dv为273 mm，计算结果如图16所示。

图16 e/D对全环板KK型节点极限承载力的影响Fig.16 The influence of e/D on the ultimate strength of KK-

从图16可以看出，随着e/D的增大，各节点承载力的变化趋势基本一致。当环板高度较小，R=40 mm时，在偏心距由0增加到-1/8D的过程中，节点的承载力存在一个小幅上升，e继续增加，节点的承载力又开始出现下降或基本保持不变。当环板高度较大，R=60、80 mm时，在e=0增加到e=-1/2D的过程中，节点的承载力一直下降。

4 KK型管板连接节点极限承载力计算方法

4.1 KK型管板节点等效受力模型

输电塔KK型管板节点受力模型如图17所示。各支管轴力拉压力成对出现且大小相近，近似认为P1=P2=P3=P4。此外，各支管轴线与主管轴线的夹角θ1、θ2、θ3、θ4一般也较为接近。

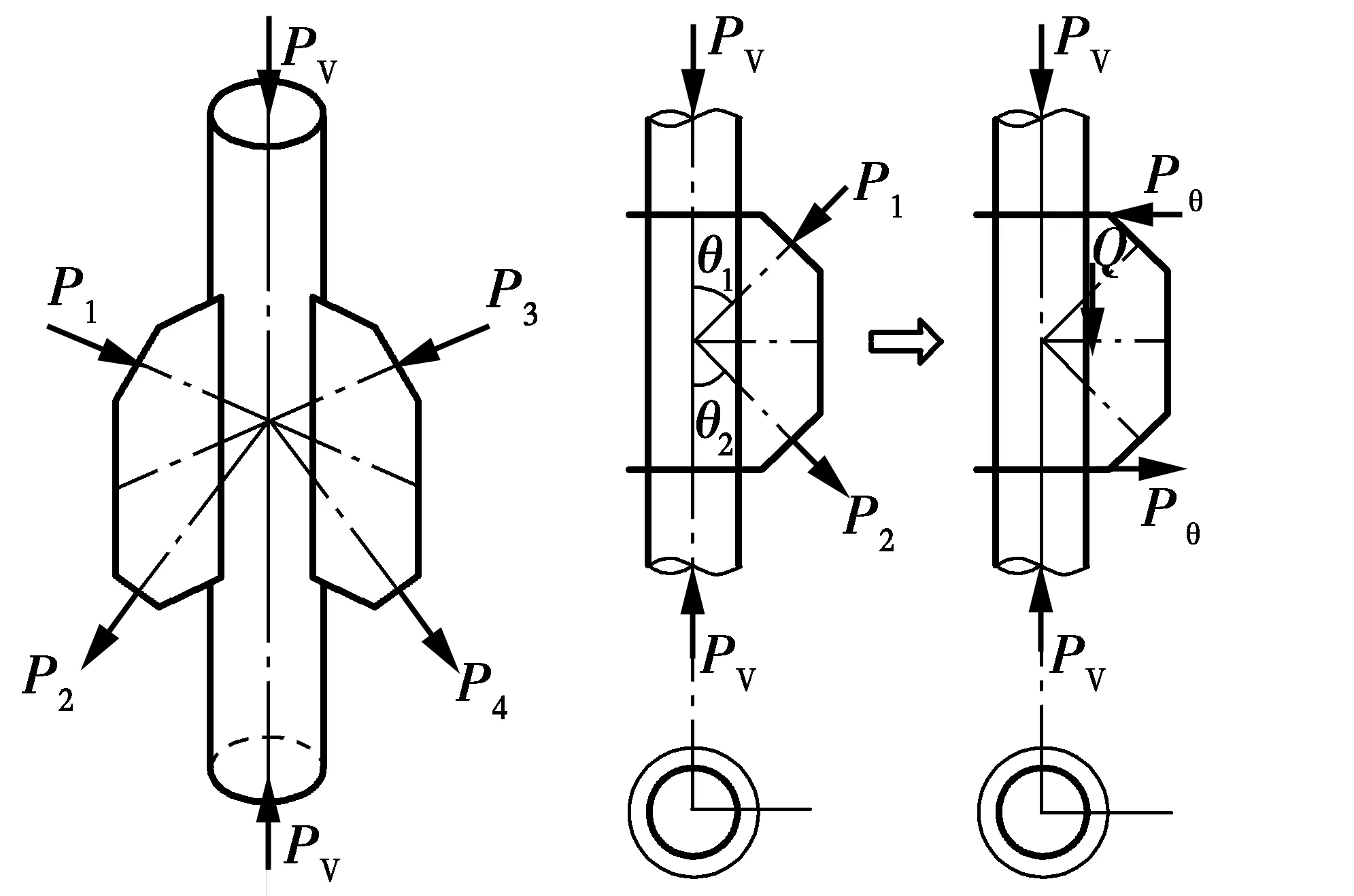
图17 KK型节点受力示意图Fig.17 The schematic diagram of KK-

对KK型管板节点的受力特点分析发现：支管对主管的轴力作用可以简化为剪力Q和等效弯矩M，M又可以等效垂直主管的力Pe，节点等效受力模型如图18所示。等效弯矩M、剪力Q以及等效横向力Pe与支管轴力P1、P2的计算关系为

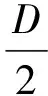
(1)

(2)

Q=P1cos θ1+P2cos θ2

(3)

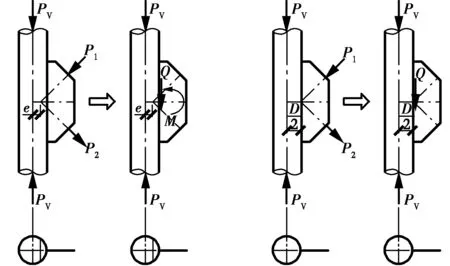
图18 KK型节点等效计算模型Fig.18 The equivalent calculation model of KK-

当支管采用负偏心连接时，各支管上的轴力仍可等效为弯矩M和竖向合力，节点等效受力模型如图18所示，此时等效弯矩M的计算公式为

M负偏心=(P1cos θ1+P2cos θ2)·(D/2+e)

(4)

从式(4)中可看出，当节点采用负偏心连接时，主管管壁所受到的弯矩作用变小，在其他条件不变的情况下，负偏心节点的承载力将得到提高。但若负偏心距较大，如图18所示，e=-D/2时，M=0，此时各支管轴力通过节点板的传递所引起的主管管壁上的竖向剪力Q将对节点的极限承载力起控制作用，由于主管管壁所受剪力过大，造成节点过早出现局部屈曲破坏，节点承载力下降。

4.2 KK型管板连接节点极限承载力建议计算方法

4.2.1 无偏心全环板KK型节点承载力计算方法 在大量有限元参数计算分析的基础上，得到无偏心全环板空间KK型节点在第一类破坏模式下的极限承载力的建议计算公式为

(5)

当主管受压时，η对节点承载力有较大影响，并且主管轴力Pv与等效横向力Pe之间存在一定的相关关系，得到Pv与Pe存在如下关系：

(6)

式中：Pv为主管轴力；Pv,y为主管达到屈服时的轴力值；Pe为主管无轴力作用时的等效横向力；Pe,v为主管有轴力作用时的等效横向力。

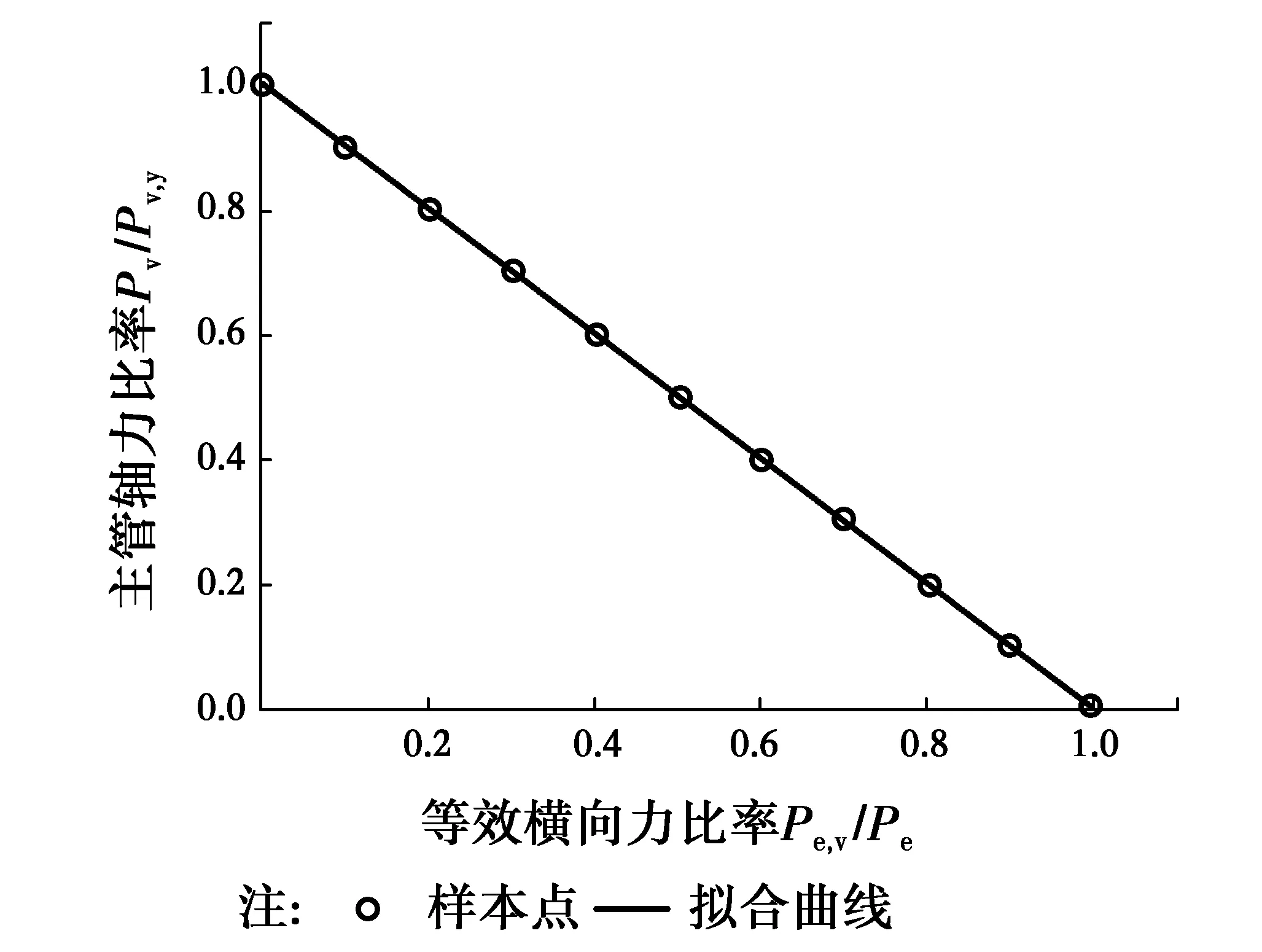
图19 KK型节点主管轴力Pv与等效横向力Pe关系曲线Fig.19 The relationship between Pv and Peof KK-joints’

图20给出了AIJ、CIDECT、CISC、JSSC和Kim的K型节点承载力计算公式值。该计算方法考虑了主管轴力、支管轴力和负偏心距的相互影响。通过式(5)可以得到节点主管无轴力作用时的等效横向荷载Pf，再通过式(2)得到主管管壁弯矩。将结果代入式(1)，便得到支管轴力。式(6)中Pv,y=fy.A。Pe可以通过式(5)求出。这样式(6)为Pv和Pe,v的关系式。只要确定了两者中一个参数，另一个参数值就求出来了。

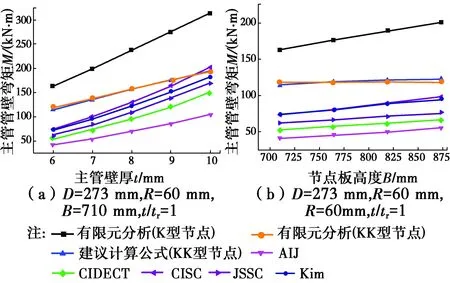
图20 节点极限承载力计算公式值与有限元值对比Fig.20 The comparison of the joints′ ultimate

从图20可知，各国规范中的平面K型管板节点承载力计算公式值均大幅低于本文全环板平面K型节点有限元值，同时也一定程度上低于本文全环板空间KK型节点有限元值。这是因为各国规范所提出的计算公式是针对无环板情况下管板节点的承载力，无法反映全环形板对节点承载力的提高作用。

4.2.2 负偏心全环板KK型节点承载力计算方法 主管轴力Pv与主管管壁剪力Q在负偏心距为e=-D/2时，参数分析拟合结果为

(7)

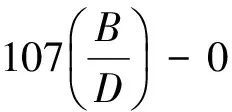
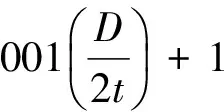
(8)

式中：Pv为主管轴力；Pv,y为主管达到屈服时的轴力值；Qu为主管在无轴力作用时的主管管壁剪力；Qu,v为主管在有轴力时的主管管壁上剪力。

在全环板KK型管板节点偏心距从e=0增加到e=-D/2的整个过程中，主管管壁的等效弯矩M和剪力Q两者之间的相关关系曲线，如图21所示。

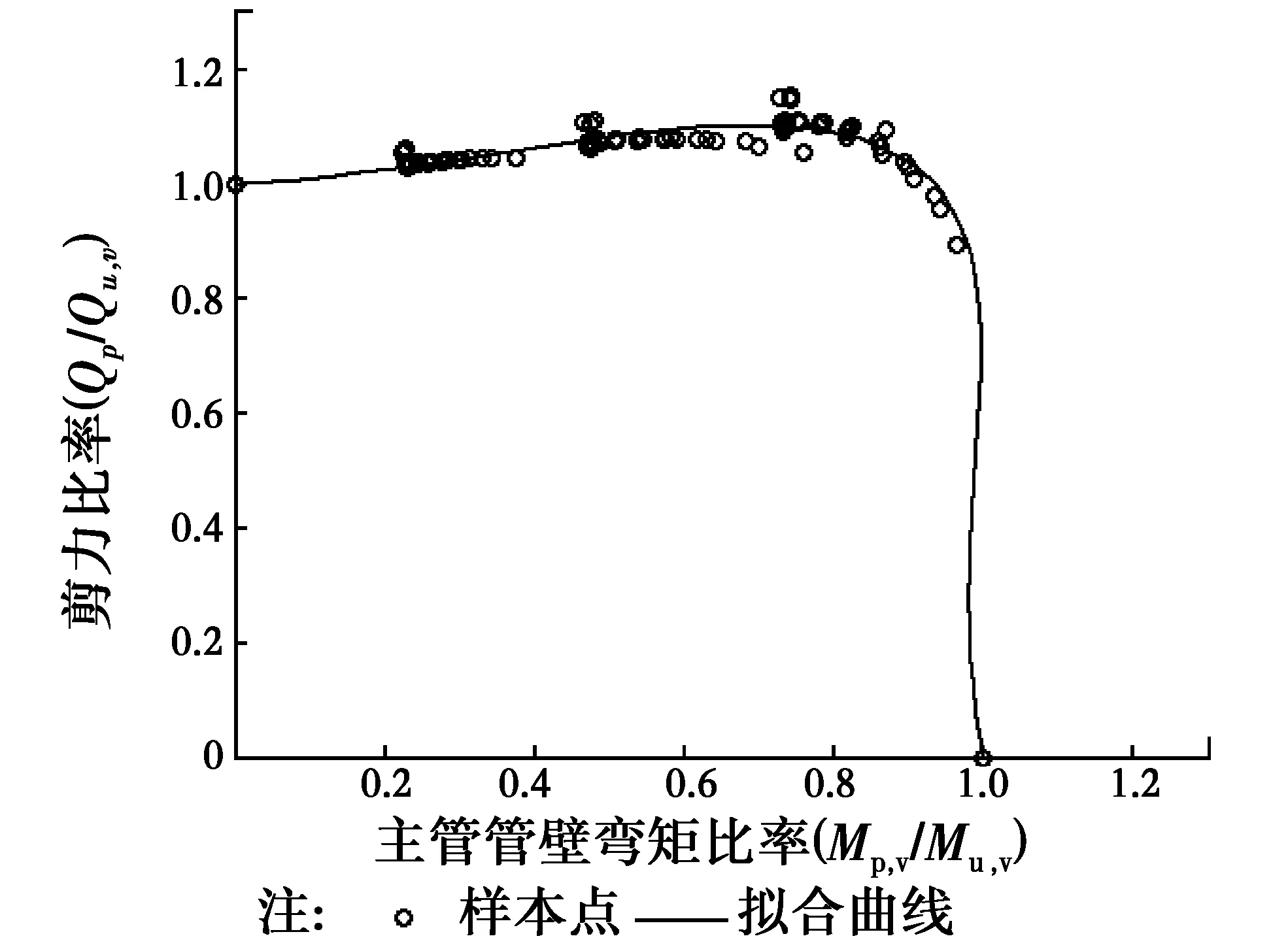
图21 KK型节点主管管壁剪力Q与主管管壁弯矩M关系曲线图Fig.21 The relationship between Q and M of KK-joints’

当节点采用负偏心连接时，设主管管壁等效弯矩比率m=Mp,v/Mu,v与剪力比率n=Qp,v/Qu,v之间的关系等式为

m4+0.6088 m3n-1.13 m2n2-

0.295 mn3+n4=1

(9)

式中：Mp,v为主管受轴力，且节点存在负偏心时的主管管壁等效弯矩；Mu,v为主管受轴力，且节点偏心距e=0时的主管管壁等效弯矩；Qp,v为主管受轴力，且节点存在负偏心时的主管管壁剪力；Qu,v为主管受轴力，且节点负偏心距e=-D/2时，其主管管壁上的剪力。公式(9)实际反映了负偏心作用下主管管壁剪力Q与等效弯矩M及主管轴力Pv三者的关系。在实际的工程设计中，由KK型管板节点的各几何尺寸参数，通过式(8)可以得到主管无轴力作用的情况下节点在偏心距e=-D/2时主管管壁上的剪力Qu, 将Qu代入式(7)即可得到主管有轴力时的Qu,v。

在节点采用负偏心连接，且偏心距为e时，等效弯矩M与剪力Q之间存在关系

(10)

结合式(9)，即可得到不同偏心节点在主管有轴力作用时，其主管管壁上的弯矩M和剪力Q。

5 结论

对两类空间KK型管板节点进行了研究，通过有限元参数分析探讨了几何无量纲参数、主管应力水平等对节点极限承载力的影响变化规律：

1) 对于无偏心全环板KK型节点，全环板使得主管径向刚度得到增强，节点承载力显著提高。相比无环板节点，全环板KK型节点与对应K型节点承载力的降幅进一步增大。β变化对节点承载力影响很小；当D/t减小时节点承载力大幅提升；B/D增加对节点承载力提高作用很小；R较小时，R增加对节点承载力有明显提高，但超过一定值后，R继续增加带来的提高作用很小；tr增加仅在R较小时对节点承载力有明显提升；主管受压时，随着η增大，节点承载力直线下降。

2) 对于负偏心全环板KK型节点，采用负偏心连接基本不能提高节点承载力，相反会产生不利作用，在该类节点的设计中不建议使用负偏心的连接方式。

3) 结合大量有限元参数分析，针对无偏心全环板KK型节点，提出了基于主管控制的节点承载力计算公式；针对负偏心全环板KK型节点，在节点发生局部屈曲破坏模式下，提出了考虑负偏心作用的节点承载力计算公式。通过建议计算方法可以估算第一类破坏模式下节点极限承载力，用于指导实际工程设计。

[1] 杨建平. 架空输电线路钢管塔结构[M]. 北京：中国电力出版社， 2011. YANG J P. Steel tubular tower structures of overhead transmission line [M]. Beijing：China Electric Power Press，2011. (in Chinese)

[2] 李明浩. 钢管塔插板节点与相贯线节点及试验设备的研究[D]. 上海：同济大学，2003. LI M H. Studies on gusset and direct connections tubular joints of steel tower and testing machine for connections[D]. Shanghai： Tongji University，2003. (in Chinese)

[3] 黄誉. 输电线路钢管塔节点强度理论与试验研究[D]. 上海：同济大学，2010. HUANG Y. Experimental and theoretical studies on steel tubular joints of transmission tower [D]. Shanghai：Tongji University，2003. (in Chinese)

[4] 邓洪洲，姜琦，黄誉. 输电钢管塔K型管板节点承载力试验及参数[J]. 同济大学学报(自然科学版)，2014，42(2)：226-231. DENG H Z，JIANG Q，HUANG Y. Experimental investigation and parametric studies on ultimate strength of K-type tube-gusset plate connections in transmission towers [J]. Journal of Tongji University (Natural Science)， 2014，42(2)：226-231. (in Chinese)

[5] 白强，舒爱强，包永忠. 剪力对钢管塔K型节点局部承载力的影响[J]. 电力建设，2011，32(2)：19-23. BAI Q，S A Q，BAO Y Z. The impact of shear forces on the local bearing capacity of steel tubular tower K-joints [J]. Electric Power Construction，2011，32(2)：19-23. (in Chinese)

[6] 童乐为，孙建东，王斌，等. 空间KK形圆管搭接节点静力性能试验研究与有限元分析[J]. 建筑结构学报， 2013，34(2)：91-98. TONG L W，SUN J D，WANG B，et al. Experimental study and numerical analysis on static behavior of multiplanar overlapped CHS KK-joints [J]. Journal of Building Structures，2013，34(2)：91-98. (in Chinese)

[7] 高耸结构设计规范: GB 50135—2006 [S]. 北京：中国计划出版社，2007. Code for design of high-rising structures: GB 50135-2006 [S]. Beijing：China Planning Press，2007. (in Chinese)

[8] 架空输电线路杆塔结构设计技术规定: DL/T 5154—2012[S]. 北京：中国计划出版社，2013. Technical code for the design of tower and pole structures of overhead transmission line: DL/T 5154-2012 [S]. Beijing：China Planning Press，2013. (in Chinese)

[9] 王肇民，马人乐. 塔式结构[M]. 北京：科学出版社，2004. WANG Z M，MA R L. Tower structures [M]. Beijing： Science Press，2004. (in Chinese)

[10] LYU B H，CHEN Z Q，LI H，et al. Research on the ultimate bearing capacity for steeltubular transmission tower’s joints with annular plate [J]. Applied Mechanics and Materials， 2012，166：379-384.

[11] 刘红军，李正良，白强. 基于负偏心的钢管插板连接的极限承载力[J]. 华南理工大学学报(自然科学版)，2010，38(4)：112-118. LIU H J，LI Z L，BAI Q. Ultimate bearing capacity of steel tube-gusset plate connections considering negative eccentricit [J]. Journal of South China University of Technology (Natural Science Edition)，2010，38(4)：112-118. (in Chinese)

[12] 刘红军. 特高压钢管输电塔插板连接K型节点的受力性能及承载力研究[D]. 重庆：重庆大学，2010. LIU H J. Behaviors and ultimate strength of steel tubular K-joints with gusset plate connections in UHV transmission tower [D]. Chongqing：Chongqing University，2010. (in Chinese)

[13] KIM W B. A study on connections of circular hollow section with gusset plate [J].Architectural Inst Korea，1997，13(3)：263-271.

[14] KIM W B. Ultimate strength of tube-gusset plate connections considering eccentricity [J]. Engineering Structures，2001，23(11)：1418-1426.

[15] YURA J A，EDWARDS I F，ZETTLEMOVER N. Ultimate capacity of circular tubular joints [J]. American Society of Civil Engineers，2014，107(10)：1965-1984.

Ultimate strength analysis of KK-type tube-gusset plate connections in transmission steel tubular tower

LiuKun1,LiZhengliang1,YouJun2,TuYin1

(1. School of Civil Engineering, Chongqing University, Chongqing 400030, P.R. China;2. Chongqing Design & Research Institute, China Coal Technology & Engineering Group, Chongqing 400039,P.R. China)

Multiplanar KK-type tube-gusset plate connections are the main joint types in transmission steel tubular tower, the safety of the joints are critical to the entire tower. Compared to K-joints, the mechanic characteristics of KK-joints are more complex after considering the multiplanar effects in the actual structure. Based on the bearing capacity test of K-type tube-gusset plate connections, parameterization analysis on the two kinds KK-type tube-gusset plate connections are conducted respectively, the geometric parameters and the axial force of the main tube together with other factors on the influence of the ultimate bearing capacity of multiplanar KK-joints are studied in detail. According to the results of large scale finite element parametric analysis, and considering the influence of various factors on the ultimate strength of the joints, calculation formulas of KK-type tube-gusset plate connections ultimate bearing capacity are proposed.

transmission steel tubular tower; KK-type; tube-gusset plate connections; ultimate strength

2016-03-21

重庆市科技项目基础与前沿研究计划(CSTC2C2015JCYJA00041)

刘堃(1992-)，男，主要从事结构工程研究，(E-mail) lkace001@163.com。

Foundation item：Science and Technology Project Foundation and Advanced Research Plan of Chongqing(No. CSTC2C2015JCYJA00041)

10.11835/j.issn.1674-4764.2016.06.010

TU392.3

A

1674-4764(2016)06-0072-11

Received:2016-03-21

Author brief：Liu Kun(1992-), main research interest: structural engineering, (E-mail) lkace001@163.com.