谱聚类在给水管网分区优化中的应用

刘俊，周鹏

(燕山大学 建筑工程与力学学院，河北 秦皇岛 066004)



谱聚类在给水管网分区优化中的应用

刘俊，周鹏

(燕山大学 建筑工程与力学学院，河北 秦皇岛 066004)

利用图划分技术和图论算法实现给水管网分区。根据给水管网分析，确定分区数量，建立权重邻接矩阵并计算图拉普拉斯矩阵及其特征向量，通过多路图划分对隐藏在特征向量中的聚类信息进行数据挖掘，采用遗传算法和K均值方法实现最佳节点聚类。利用PageRank和最短路径算法确定水表和阀门位置，最终实现给水管网优化分区。实际给水管网模型分区实例表明所提方法在给水管网分区的有效性。

给水管网；分区；聚类；优化

给水管网分区是在系统性能影响最小的情况下通过安装阀门、水表形成独立供水区域，便于优化调度、漏损控制等各方面的管理，以适应信息化、智能化、精细化的要求[1-5]。管网分区目的是获得规模均等，压力、水质均衡的分区。由于管网的高度复杂性以及众多技术要求和制约因素，使得分区这一问题面临较大挑战。

目前，管网分区优化方法主要有图论算法和复杂网络聚类算法。图论分区算法主要使用搜索算法获得管网拓扑结构。其中，广度优先搜索算法在DMA规模约束下，搜索与某一节点路径最短的节点集，当满足设定规模时，搜索终止，则可得到满足要求的分区。这类方法可获得各种分区方案供决策者选定[6]，或者通过模型分析获得水力最优方案[7]。相比于广度优先搜索算法的局部搜索，深度优先搜索算法可从整体上获得给水管网树状结构，并通过优化算法获得减压阀最佳位置，进而实现分区[8],或者确定各水源供水范围[9]。另外，也可以最短路径算法为基础，通过压力均衡性确定分区[10]，或者通过管道介数中心性选定阀门、水表位置，以实现分区[11]。

在复杂网络聚类中，同一聚类内节点连接紧密，而不同聚类间节点连接相对稀疏，这与管网分区的内在要求一致。相应聚类算法包括计算机科学中的图划分和社会学中的社团发现。图划分将复杂网络聚类转换为优化问题，如Nardo等[12]人使用多层次递归二分法自动获得规模均等的分区布局。社团发现则将分区问题转换为模块度等启发式规则的设计问题，其中刁克功等[13]在管网分区中首次引入社区发现贪心算法进行给水管网分区。Giustolisi等[14]引入管道权重提出了给水管网设施模块度，可以发现更小规模的结构。另外,也有其他相似度的度量方式用于给水管网分区，如按照节点位置信息采用K-均值聚类，以此为基础形成供水管网规划方案[15]，或者按照节点水压波动相似性分区，确定最优压力监测点[16]。

笔者提出一种基于复杂网络谱聚类和图论算法的给水管网分区方法。目的是在尽量降低分区不利影响的前提下，根据给水管网拓扑结构，利用数据挖掘发现隐含在其中的结构聚类信息，确定节点聚类，继而实现满足要求的分区。

1 给水管网分区方法

所提出的分区流程主要包含3个部分：

1)数据输入：管网分析与模拟，确定分区数量，建立权重矩阵。

2)实现分区：图拉普拉斯矩阵求解，根据第二特征向量，采用多路图划分确定各分区内节点聚类，即确定分区范围。

3)确定阀门、水表位置：PageRank算法确定每个分区中心节点，水源到该节点的最短路径中确定水表位置，其他分区间连接管道则为阀门位置。

1.1 给水管网分区数量的确定

给水管网分区数量需要根据分区目的、系统规模、分区大小、成本等综合确定。本方法旨在通过发现给水管网内在聚类结构，实现分区设计，因此，在获得指定数量的分区时，每个分区的规模不是严格相同。

1.2 规范化拉普拉斯矩阵

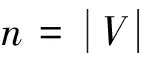
(1)

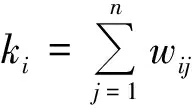
(2)

图的拉普拉斯矩阵为L=D-A，其元素Lij表示为

(3)

矩阵L的所有特征值称为图G的拉普拉斯谱，最小特征值λ1对应的特征向量称为第一特征向量，不包含任何聚类信息，所需要的聚类信息存在于其他的特征向量，称为第二特征向量。

传统图划分最小割算法以最小化割边为目标，这可能导致分区时规模的不均衡。为此采用规范化割集准则，规范化拉普拉斯矩阵为

(4)

谱平分法利用第二小特征值对应的特征向量实现两个分区的优化划分。如果需要得到多个分区，则需要对子分区重复该方法。为了提高分区效率，采用NJW多路谱算法[17]，即根据多个第二最小特征向量，通过聚类算法直接获得指定数量的分区。矩阵E的最大特征值为1，其他特征值均小于1。对于社团结构比较明显的管网，有些特征值接近于1，其对应的第二特征向量中，同一社团内部节点的值接近。对于社团结构不明显的一般给水管网，少量第二特征向量也可获得良好分区[18]。第二特征向量确定方法如下：

1)确定管道权重。管径、流量大的管道承担的输配水功能越重要，两节点连接越紧密，选择管道权重为wij=DijQij，Dij、Qij分别为管道ij的管径与流量。

2)计算矩阵E前k-1个最大的第二特征值所对应的特征向量，x1,…,xk-1，构造矩阵X=[x1,…,xk-1]∈Rn×(k-1)。

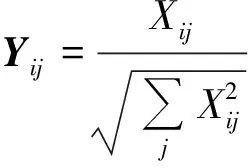
4)将Y的每一行看做Rk-1空间中的一个点。

1.3 基于遗传算法的谱聚类

给水管网分区信息可通过特征向量数据挖掘方法获得。本文采用遗传算法与K均值算法实现数据挖掘。K均值算法将属性相同的点划分到一个聚类，并用聚类中心代表该聚类。聚类质量由误差平方和度量，见式(5)。

,ci)2

(5)

式中：SSE为误差平方和；Ci为某个聚类i；ci为聚类中心，代表某个聚类；y为空间点；dist为空间点的欧几里得距离；m为聚类个数。

K均值算法取决于初始化聚类中心，是一种局部优化算法。为了实现最优化分区，采用遗传算法优化聚类中心。种群中每个个体对应于各个聚类中心，以SSE最小化为目标函数，通过线性排序确定个体适应度，交叉、变异逐渐产生新的子代。为了提高搜索速度，在每次得到聚类划分后，用校正后的聚类中心代替个体中原来的聚类中心。

1.4 确定阀门、水表位置

在确定分区范围后，接下来要确定水表和阀门的位置。在每个分区中均存在中心节点，一般是拓扑连接紧密的节点，即度较高的节点，这意味着该节点是流量的枢纽节点，则水源到该枢纽节点的最短供水路径应该是该分区的主要供水路径，主要供水路径必经过分区间连接管道，则这个管道即为进水点，也就是水表位置，其他连接管道则为阀门位置。本文中将给水管网视为权重无向图，利用PageRank算法确定各节点的中心性。设每个节点的中心性为xi，节点i的中心性与它的邻居节点中心性呈正比。

(6)

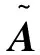
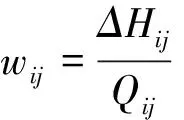
1.5 分区均衡性

每个分区规模应相当，分区内压力应均衡。为此提出两个分区评价指标。

1)分区规模均衡性SU

(7)

式中：Si为节点用水量；M为分区数量；N为管网用水节点数；n为每个分区内用水节点数。

各分区SU越接近，分区规模越均衡。

2)压力均衡性PU

(8)

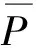
1.6 分区间运行关系

DMA按进水点数量和流量关系可分为单进口、多进口和串联DMA，如图1所示，其中，DMA2和DMA3为单进口类型，DMA4为多进口，上述3个分区共同特征是均只有流量流入而无流出。而DMA1除满足本区用水外，还需向DMA2供水，因此，DMA1为串联类型，有流量的流入和流出。目前的分区方法为了方便管理并减少计量误差，一般DMA设计优先选择单进口、无流出类型[19]。但DMA设计影响因素多、情况复杂，有时难以满足上述原则，同时单进口DMA也存在系统弹性能力降低、难以满足消防流量要求和末端水质下降等问题，因此，根据具体情况也可选择多进口DMA，但进水口数量不宜太多，否则进水点处减压阀会引起压力波动[20]。可采用主、副进水口设计，即在正常供水时只开启主进水口，而当高峰用水或消防时，可开启副进水口。当远离干管的DMA其供水路径需要经过其他分区时，或者管理、技术等多因素综合比较后串联DMA具有优势时，也可选择串联类型DMA。

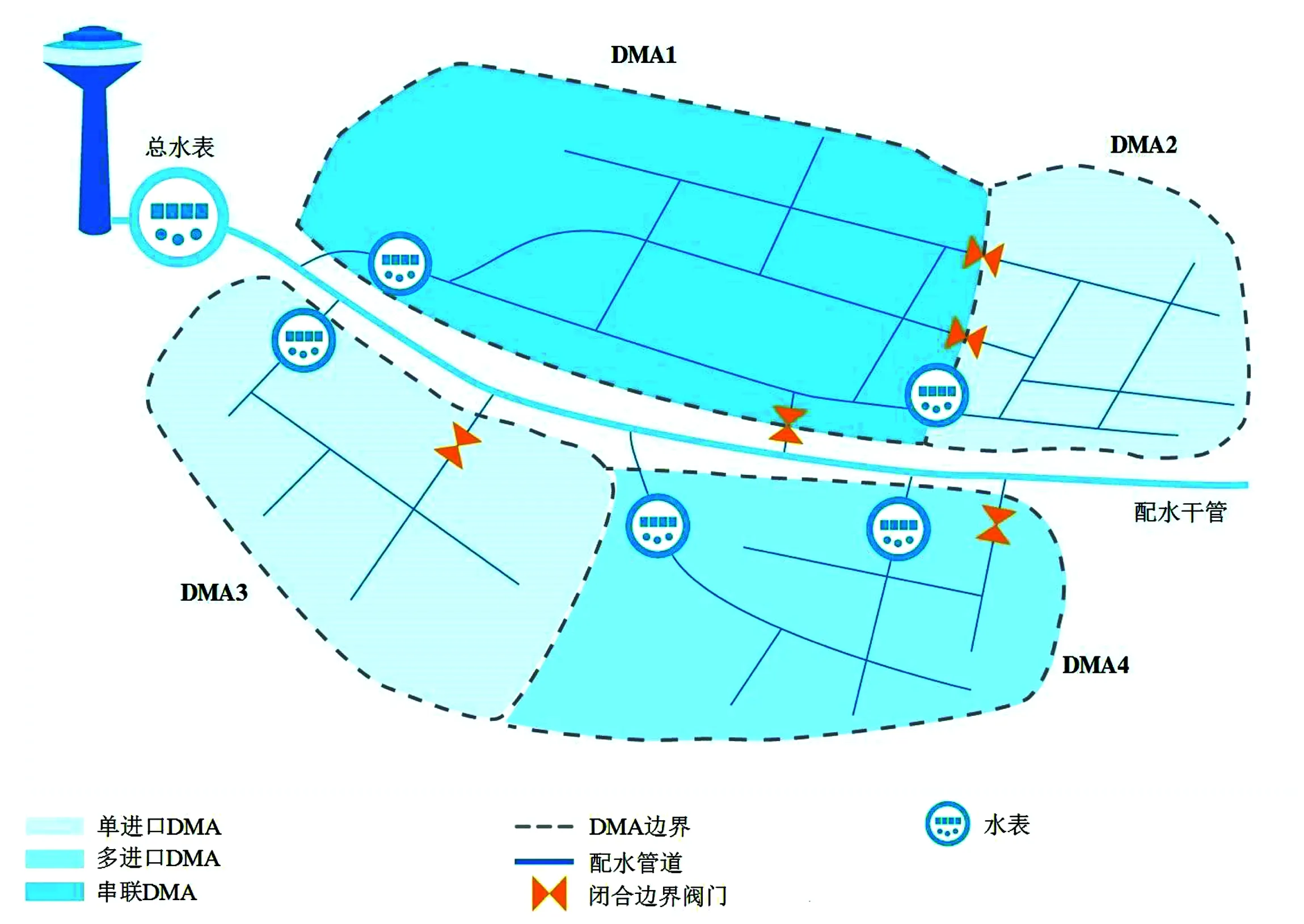
图1 DMA类型及运行关系[21]Fig.

2 分区实例

以图2所示环状给水管网[22]为例验证所提分区方法的有效性。该给水管网含有1个水源，36个用水点，58根管道，具有复杂的环状结构。设定分区数量为4个。

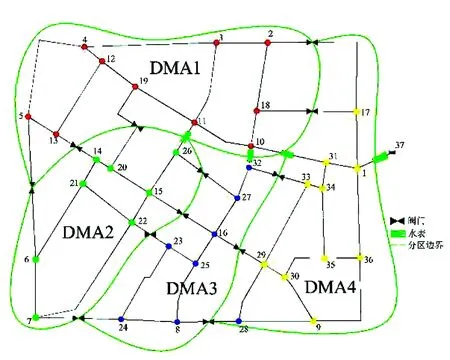
图2 4个分区的给水管网结构Fig.

4个分区的方案如图2所示。每个分区的规模可见表1，从表中可知每个分区的规模与平均规模有一定偏差。如前所述，如果分区时强调每个分区应含有相同的规模(用水量)，则必将破坏给水管网内部的聚类结构。而依据聚类算法，属性相似的节点组成一个分区，这可从整体上降低分区对给水管网结构的影响。分区后的压力分析见表2。由表2可知，每个分区压力范围相似，平均压力有微小差别。压力均衡性较好，PU值均低于平均压力的10%，说明分区后管网性能没有明显降低，对系统性能的影响较小。

表1 分区规模分析

Table 1 Analysis of size of DMAs

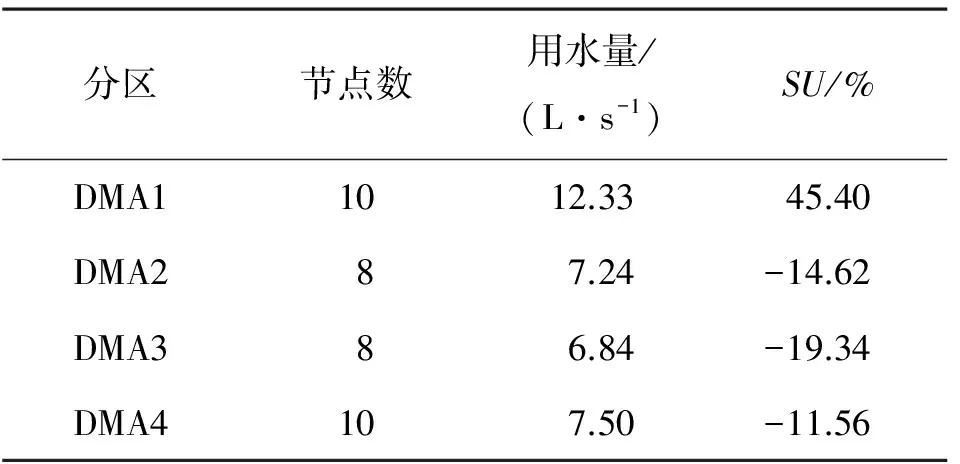
分区节点数用水量/(L·s-1)SU/%DMA11012．3345．40DMA287．24-14．62DMA386．84-19．34DMA4107．50-11．56

表2 分区压力分析

Table 2 Analysis of pressure of DMAs

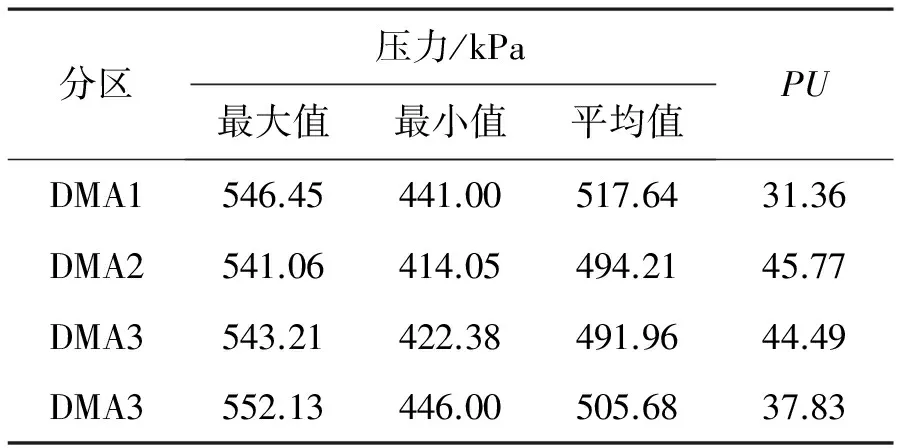
分区压力/kPa最大值最小值平均值PUDMA1546．45441．00517．6431．36DMA2541．06414．05494．2145．77DMA3543．21422．38491．9644．49DMA3552．13446．00505．6837．83

K均值算法是局部优化方法，遗传算法是一种全局优化方法，二者结合将增加收敛速度，由图3可知，经过25次进化后种群即实现收敛。另外，每一代的最佳个体都能搜索到最佳聚类。

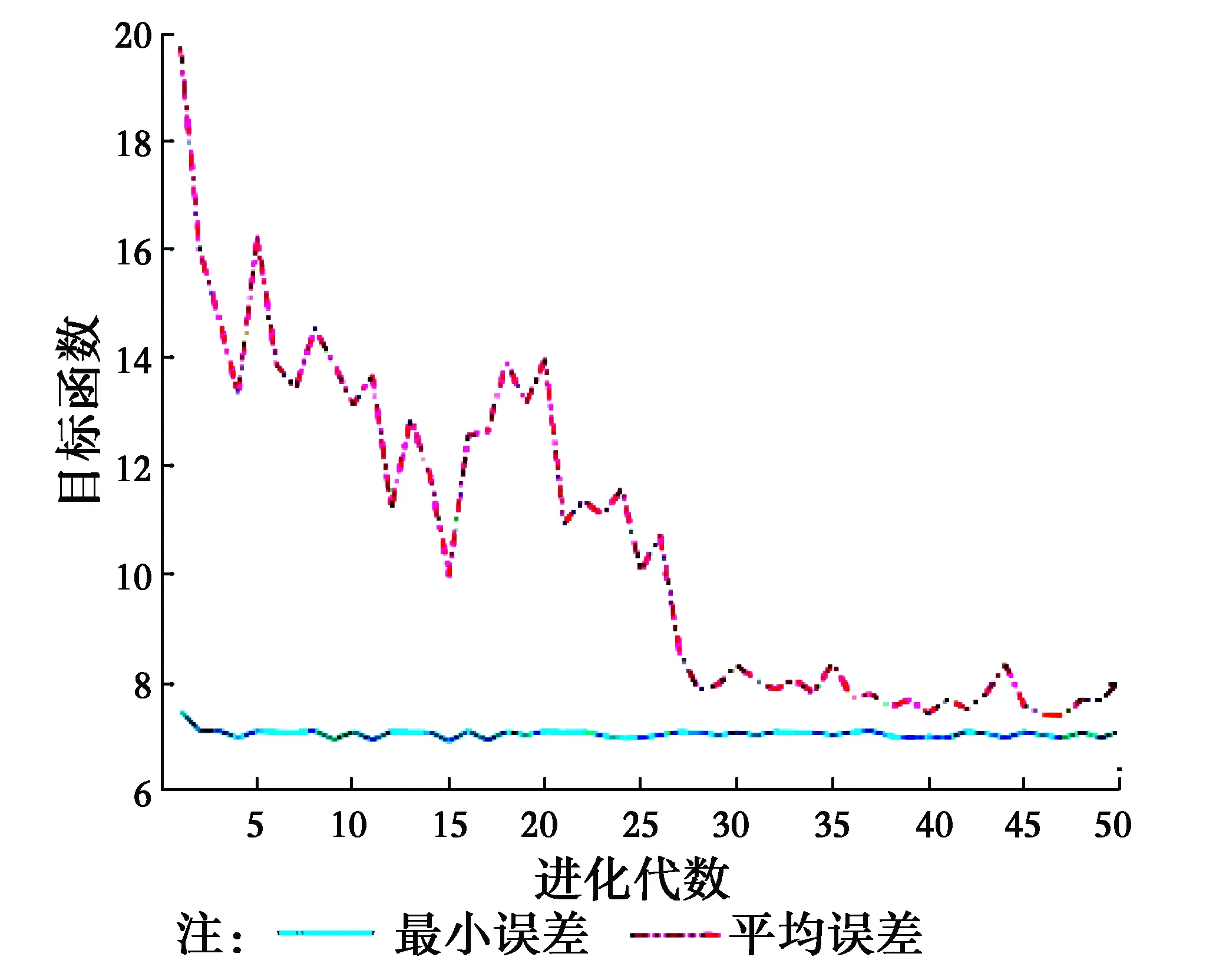
图3 最优解及种群收敛变化Fig.

在确定分区边界后，需要确定每个分区的进水点和设置阀门的管道。为此根据PageRank算法分析每个节点的中心性，给水管网末端节点中心性较低，中心性较高的前1/3节点见图4。

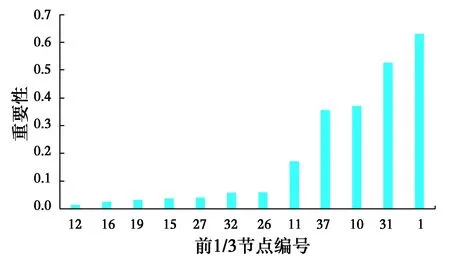
图4 部分节点中心性Fig.

利用最短路径算法可得每个分区水表位置，其他分区边界管道则为阀门位置。由图2分区结构可知，基于谱聚类的分区方法将干管节点也纳入分区，因此,DMA1和DMA4具有流量流入流出，为串联分区，DMA2和DMA3则为单进口分区。串联分区结构的引入，使得DMA1和DMA4内节点分区前后水流路径不变，分区对这些节点没有影响。

3 结论

提出了基于谱聚类的给水管网分区方法，同时可确定每个分区的进水点和阀门位置，并以一个真实给水管网说明本分区方法的可行性。本方法将给水管网拓扑结构通过谱方法映射到高维向量空间，并依据聚类将拓扑相似节点划分到一个分区，遗传算法与K均值算法相结合提高了算法效率，同时,本方法具有较强的健壮性，可根据要求实现不同规模的分区设计。

本文中不仅确定了分区边界，也给出了进水点位置，下一步工作可在此基础上通过优化进水点减压阀，将各分区内压力控制在合理范围，从而在整体上降低漏损。

[1] MORRISON J, TOOMS S, ROGERS D. District metered areas guidance notes [M]. London: IWA Publication, 2007.

[2] 刘俊, 孙佳, 俞国平. 分区供水技术在漏损控制中的研究现状与进展[J].中国给水排水, 2010, 26(16):7-10. LIU J, SUN J, YU G P. Current situation and progress of water distribution system zoning technologies for water loss control [J]. China Water & Wastewater, 2010, 26(16):7-10. (in Chinese)

[3] 凌文翠, 张涛, 强志民, 等. 城市供水管网独立计量区域的研究与应用进展[J].中国给水排水, 2011, 27(13):46-50. LING W C, ZHANG T, QIANG Z M, et al. Research and application of district metering area for urban water distribution network [J]. China Water & Wastewater, 2011, 27(13):46-50. (in Chinese)

[4] 李树平. 日本给水管网布局理论与启示[J].中国给水排水, 2014, 30(22):46-49. LI S P. Review of Japanese theory on water distribution system layout [J]. China Water & Wastewater, 2014, 30(22):46-49. (in Chinese)

[5] 许刚, 朱子鹏, 刘文杰, 等. 大规模供水管网分级分区计量应用研究[J]. 给水排水, 2014, 30(22):96-98. XU G, ZHU Z P, LIU W J, et al. Application of district metered areas in large scale water distribution system [J]. Water & Wastewater Engineering, 2014, 30(22):96-98. (in Chinese)

[6] FERRARI G, SAVIC D, BECCIU G. A graph theoretic approach and sound engineering principles for design of district metered areas [J]. Journal of Water Resources Planning and Management, 2014, 140(12): 04014036.

[7] ALVISI S, FRANCHINI M. A heuristic procedure for the automatic creation of district metered areas in water distribution systems [J]. Urban Water Journal, 2014, 11(2): 137-159.

[8] AWAD H, KAPELAN Z, SAVIC D. Optimal setting of time-modulated pressure reducing valves in water distribution networks using genetic algorithms [C] // Boxall & Maksimovié. Integrating Water Systems (CCWI 2009 Conference). London: Taylor & Francis Group, 2009:31-37.

[9] DI NARDO A, DI NATALE M, SANTONASTASO G F, et al. Water network sectorization based on graph theory and energy performance indices [J]. Journal of Water Resources Planning and Management, 2014, 140(5): 620-629.

[10] 张楠. 城市供水管网分区管理技术优化研究[D]. 天津: 天津大学, 2012. ZHANG N. District metered areas optimization for water distribution systems [D]. Tianjin: Tianjin University, 2012.

[11] 刘俊, 俞国平. 结合图论与地理信息系统的供水管网分区优化[J]. 同济大学学报(自然科学版), 2012, 40(12): 1863-1869. LIU J, YU G P. Integration of graph theory systems and GIS for district metered areas of water distribution [J]. Journal of Tongji University (Natural Science), 2012, 40(12): 1863-1869. (in Chinese)

[12] DI NARDO A, DI NATALE M, SANTONASTASO G F, et al. An automated tool for smart water network partitioning [J]. Water Resour Manage, 2013, 27(13): 4493-4508.

[13] DIAO K G., ZHOU Y W, RAUCH W. Automated creation of district metered area boundaries in water distribution systems [J]. Journal of Water Resources Planning and Management, 2013, 139(2): 184-190.

[14] GIUSTOLISI G, RIDOLFI L. A novel infrastructure modularity index for the segmentation of water distribution networks [J]. Water Resources Research, 2014, 50(10): 7648-7661.

[15] 叶健, 高金良, 刁美玲, 等. 分形理论在城市供水管网规划中的应用研究[J]. 工程设计学报, 2014, 21(6):562-565. YE J, GAO J L, DIAO M L, et al. Application study on urban water supply network planning based on fractal theory [J]. Journal of Engineering Design, 2014, 21(6):562-565. (in Chinese)

[16] 何忠华, 袁一星. 基于分区模型的城市供水管网压力监测点布置[J]. 哈尔滨工业大学学报, 2014, 46(10):37-41. HE Z H, YUAN Y X. Layout of pressure monitoring system based points in urban water distribution on district model [J]. Journal of Harbin Institute of Technology, 2014, 46(10):37-41. (in Chinese)

[17] NG A Y, JORDAN M I, WEISS Y. On spectral clustering: Analysis and an algorithm[C]// Dietterich T G, Becker S, Ghahramani. Advances in Neural Information Processing Systems, Cambridge, MA, MIT Press, 2002, 14: 849-856.

[18] CAPOCCI A, SERVEDIO V D P, CALDARELLI G, et al. Detecting communities in large networks [J]. Physica A, 2005, 352(2/3/4):669-676.

[19] FERRARI G, SAVIC D, BECCIU G. A graph theoretic approach and sound engineering principles for design of district metered areas [J]. Journal of Water Resources Planning and Management,2014, 140(12): 1-13.

[20] PRESCOTT S, ULANICKI B. Improved control of pressure reducing valves in water distribution networks [J]. Journal of Hydraulic Engineering, 2008,134(1): 56-65.

[21] FARLEY M. Leakage management and control: A best practice training manual [M]. WHO, 2001.

[22] BRAGALLI C, D'AMBROSIO C, LEE J, et al. On the optimal design of water distribution networks: a practical MINLP approach [J]. Optimization and Engineering, 2012, 13(2)： 219-246.

(编辑 王秀玲)

Spectral clustering for optimal design of district metered areas in water distribution systems

LiuJun，ZhouPeng

(College of Civil Engineering and Mechanics, Yanshan University, Qinhuangdao 066004, Hebei, P. R. China)

Design of district metered areas(DMAs) in water distribution system was performed based on complex network spectral clustering and graph theory. First the number of DMAs was determined, and graph weighted adjacency matrix and Laplacian matrix were established. Thenk-way spectral clustering algorithm was used to discover the optimal clusters hidden behind eigenvectors of Laplacian matrix, leading to the best layout of DMAs using genetic algorithm andK-means. PageRank and shortest path algorithm were adopted to ascertain the location of meters in DMAs and valves between DMAs to achieve the optimal design of DMAs eventually. And a real water distribution system was tested and the results showed that the proposed method was effective in DMAs design.

water distribution systems；district metered area; clustering; optimization

2016-03-10

国家自然科学基金(51508492);河北省自然科学基金(E2015203079);燕山大学博士基金(B864)

刘俊(1982-),男,博士,主要从事水资源与给水排水系统设计与运行优化研究,(E-mail) sdlj2008@163.com。

Foundation item：National Natural Science Foundation of China (No. 51508492); Natural Science Foundation of Hebei Province (No. E2015203079); Doctor Foundation of Yanshan University (No. B864)

10.11835/j.issn.1674-4764.2016.06.019

TU991

A

1674-4764(2016)06-0142-06

Received:2016-03-10

Author brief：Liu Jun (1982-), assistant professor, PhD, main research interests: optimal design and operation of water resources and urban water distribution and drainage systems, (E-mail) sdlj2008@163.com.