基于图像处理技术的纸张功能信息数字化研究
张开生 侯新刚
·纸张功能信息数字化·
基于图像处理技术的纸张功能信息数字化研究
张开生1,2侯新刚1
(1.西京学院控制工程学院,陕西西安,710123;2.陕西科技大学电气与信息工程学院,陕西西安,710021)
围绕纸张功能信息数字化的图像呈现问题展开研究,采用图像处理技术,分别从数字图像的获取、傅里叶变换、离散余弦变换、哈达玛变换、Radon变换、小波变换等方面进行分析探讨,研究不同的图像变换方式在纸张功能信息图像处理中的特点。研究表明,各种图像变换方式在图像处理中的应用各有不同,在纸张功能信息数字化的应用中发挥各自的转换优势。
纸张功能;信息数字化;图像处理
纸张功能信息数字化是指采用数字化的形式来表征纸张的功能信息,即将代表特种纸种类的数字信息通过造纸湿法成形过程镶嵌在纸张中,形成具有特定功能的专用纸张[1-3]。通常人们采用磁性材料来表征纸张信息,这种方式虽然在某些方面能有效抵制仿制品的滋生,但大部分通过后期的印刷手段制作,纸张的特征表现在表面,保证不了纸张信息的唯一性,不能从根本上解决纸张的信息表达问题,并且这些都属于公众识别范畴。因此,为了增强纸张信息表达的可靠性与唯一性,从专业识别的角度对纸张进行功能信息化表达,众多学者研究探索纸张功能信息数字化表达与实现问题,而在研究上述问题时,首先要研究普通纤维与特殊纤维的混合及打浆配比控制问题[4-5],其次研究内嵌信息数字化植入问题,最后研究对纸张内嵌功能信息进行图像处理的问题。采用图像变换的方法对纸张功能的信息化呈现进行有效地分析及处理是纸张内嵌数字化信息准确呈现的关键,由此看来,采用图像处理的方法研究纸张功能信息化具有十分重要的现实意义。
1 数字图像的获取研究
在研究纸张功能信息数字化过程中,对于纸张内嵌信息数字图像的获取是图像处理的第一个环节,该环节是将模拟图像转换为适合计算机处理的图像,转换后的图像就是数字图像,因为模拟图像表达信息不便于计算机进行有关处理。图像获取的任务由图像采集系统完成,图像采集系统主要包括成像系统、采样系统及量化器[6],其示意图如图1所示。

图1 图像采集系统示意图
图1中,关系式
p
(
x
,
y
)指模拟图像,是连续的,对于二维光谱图像也是连续的,其图像数据通过成像系统函数
f
(
x
,
y
)=
h
(
x
,
y
)·
p
(
x
,
y
)转换,并输出连续图像,连续图像输入采样系统产生采样图像
g
s
(
x
,
y
)。该采样图像
g
s
(
x
,
y
)在(
x
,
y
)的整数坐标处有值,在该坐标处是唯一的,而
g
s
(
x
,
y
)的值域在该坐标处也是连续的,所以它是定义在离散空间上的函数,而且是连续的,计算机在进行数字图像处理时,要对数据进行量化处理,实际上是对每个采样点(像素)的值进行处理
[7]
。
在实际应用中,数字图像处理的主要方法有空域法和变换域法两种。常见的变换域法主要有离散傅里叶变换、离散余弦变换、沃尔什变换、哈达玛变换、霍特林变换、拉东变换和小波变换等[8]。

图2 二维傅里叶变换图
2 连续图像模型的构建与算法表征
设计与分析图像处理系统的必要手段通常是采用数学方法来表征图像。在图像表示方法中图像和图像函数是确定的,人们在分析图像的点性质时,可以此来进行分析,统计平均参数表示图像的特征时,该方法是一种统计图像的表示方法。
如果用(x,y)表示空间坐标,t表示时间,λ表示波长,那么代表像源的空间辐射能量分布为C(x,y,t,λ)。
假设0≤C(x,y,t,λ)≤A,其中A是图像的最大亮度。
为了分析简单化,假设所有图像在某一个矩形区域内非零,即:
-Lx≤x≤Lx
(1)
-Ly≤y≤Ly
(2)
另一方面,实际图像也只有在有限实际内可观察,故可令:
-T≤t≤T
(3)
对于单色图像系统来说,图像函数f(x,y,t)通常是指图像的光亮度,按照一维时间信号的标准定义,图像函数在给定点上的时间平均值为:
(4)
在实际应用中,图像随机过程f(x,y,t)完全可由它的联合概率密度来表示,对于所有样本点J,其联合概率密度为p{f1,f2,…,fJ;x1,y1,t1,x2,y2,t2,…,xj,yj,tj},其中(x1,y1,t1)代表图像函数fj(xj,yj,tj)的实际样本。因此,光亮度函数的概率密度必须采用单边密度。
3 图像处理算法研究
3.1 二维离散傅里叶变换
一维的离散傅里叶变化和快速离散傅里叶变换是二维离散信号处理的基础,一幅静止的数字图像可以看成二维的数据阵列,因此数字图像处理是二维数据处理。
对图像进行二维傅里叶变换得到的频谱图即为图像梯度的分布图。当然,频谱图上的各点与图像上各点并不存在一一对应的关系,这一点与是否采取移频处理没有关系。傅里叶频谱图上看到的明暗不一的亮点,其意义是指图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点频率的大小。一般来讲,梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅里叶变换后的频谱图,也叫功率图,可以直观地看出图像的能量分布:如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小);反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的、边界分明且边界两边像素差异较大的。为了得到图像的能量分布,需要对图像进行二维傅里叶变换,图2所示为原始图像经二维傅里叶变换后的分布图。
二维傅里叶变换是一维傅里叶变换在每一行扫描线和列扫描线上的傅里叶变换的叠加。对比二维傅里叶变换和一维傅里叶变换的结果,从图2中可以看出二维傅里叶变换后图像的能量分布体现得更全面,中心位置体现图像的主要能量,中心区域以外体现了图像的细节,使得细节更加突出。
3.2 离散余弦变换
在图像压缩中应用较广泛的是离散余弦变换,将图像变换得到的量化的DCT系数进行一次编码,并将编码进行传送,然后就形成了压缩后的图像格式[9]。对应用于纸张功能信息数字化处理,也比较适用。

图3 二维离散余弦变换图
离散余弦变换是与傅里叶变换相关的一种变换,它类似于离散傅里叶变换,但是只使用实数。离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,由于离散余弦变换具有很强的“能量集中”特性,大多数自然信号(包括声音和图像)的能量都集中在离散余弦变换后的低频部分。图3所示为图像经过二维离散余弦变换后的图像,从图3结果可以看出,相比二维傅里叶变换,离散余弦变换之后的图像能量分布更加清晰、直观。离散余弦变换需要多次乘法与多次加法,运算量及存储空间较大,图中变换能量集中在左上方,体现了图像的背景信息,向右下方扩展体现图像的细节,要求微处理器必须具有较高的性能。
3.3 哈达玛变换
哈达玛变换是实现图像变换的重要方法之一。它是一种对应二维离散的数字变换,大大地提高了运算速度。哈达玛矩阵的最大优点在于它具有简单的递推关系,具有能量集中的特性,而且原始数据中数字越是均匀分布,经变换后的数据越集中于矩阵的边角上。因此,二维哈达玛变换可用于压缩图像信息。
哈达玛变换的过程通常是先对图像进行灰度化处理,然后再对其进行哈达玛变换,这一点对图像处理至关重要,特别是在实时处理大量数据时,哈达玛变换更加显示其优越性。但是哈达玛变换的收敛速度较慢,因此对于频谱分析的效果较差,哈达玛变换在图像处理中的主要应用是压缩编码。
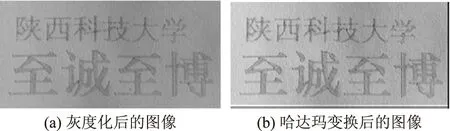
图4 哈达玛变换图
图4为基于纸张信息数字化图像的哈达玛变换图。从图4可以看出,哈达玛变换后图像的轮廓仍然清晰,对识别图像内容影响不大。此变换方式在对图像质量影响较小的情况下,可以减少存储器的存储容量,提高图像变换的运算速度。
3.4 Radon变换
Radon变换主要用于地球物理领域,其基本思想是对某个函数在给定的路径上进行积分运算,从这一基本思想出发,可以在被探测的目标体一侧放置一个源,让源产生的能量沿着一定的射线路径到达目标体的另一侧被接收。
二维情况下Radon变换大致可以这样理解:一个平面内沿不同的直线(直线与原点的距离为d,方向角为α对f(x,y)做线积分,得到的像F(d,α)就是函数f的Radon变换。也就是说,平面(d,α)的每个点的像函数值对应了原始函数的某个线积分值。
图5所示的Radon变换结果是原始图像分别在水平方向、45°方向以及垂直方向上灰度值分布情况的映射。图5反映了3个方向的Radon变换,也就是从3个方向反映了图像的投影情况,其中水平方向变换较为平缓,45°方向情况较为复杂。而实际应用中的Radon变换可以从任意角度反映图像的灰度分布情况,即可以从任意角度反映图像的投影和轮廓。这就对控制器提出了较高的要求,需要控制器能适应不同角度的Radon变换,有较高的处理速度和较强的适应性。
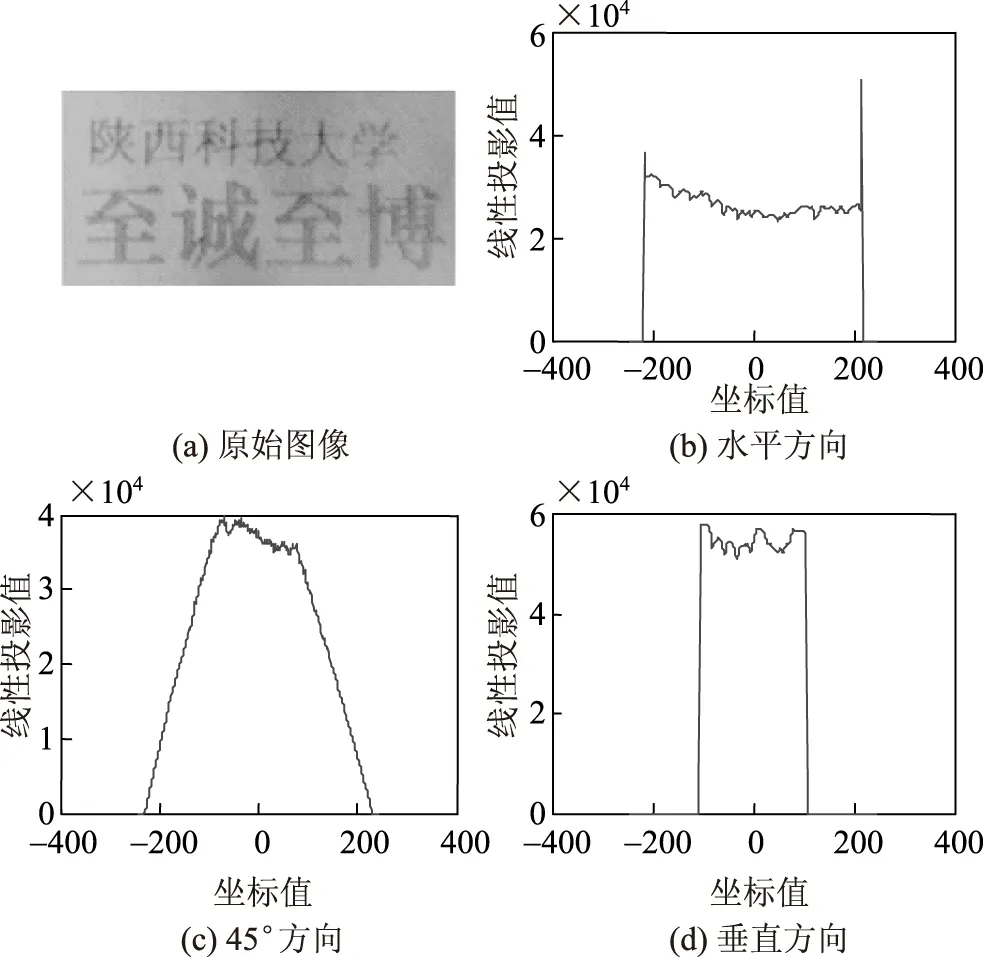
图5 Radon变换图
3.5 小波变换
小波变换可以从空间上形象地说明多分辨率的特性,小波变换完成后得到的系数是在不同的缩放因子下由信号的不同部分产生的。使用这样的缩放因子和平移参数的小波变换称为双尺度小波变换,通常离散小波变换就是指双尺度小波变换。执行离散小波变换的有效方法是使用滤波器,通过低通滤波器得到的信号为近似值A,通过高通滤波器得到的信号则为细节值D,其中细节值又分为水平细节、垂直细节及对角细节,在实际应用中,信号的低频分量往往是最重要的,而高频分量只起一个修饰作用。小波变换的MATLAB应用较多,主要表现在3个方面:图像压缩、图像去噪及图像分割。
小波变换的结果如图6所示,从图6可以看出,经过小波近似值系数变换得到的图像和原始图像比较接近,这是因为小波近似值系数变换主要体现的是图像的背景信息和主要能量。其余的3种情况从不同角度反映了原始图像的高频能量和细节信息,可看出对角方向的细节最为丰富。小波运算较为复杂,对控制器的运算能力和处理速度要求较高。

图6 小波变换图
4 结 语
纸张的功能信息数字化是一个比较复杂的问题,为了增强纸张功能信息数字化识别的可靠性与唯一性,从专业识别方面对纸张进行功能信息数字化研究。通过对上述各种图像变换方法的研究对比,可以得出傅里叶变换反映了图像能量分布情况,低频和高频分别反映了图像的背景和细节,低频成分对图像的影响较大。离散余弦变换也体现了图像的能量分布,但运算方式与傅里叶变换不同,其信息集中能力更强。Radon变换可从不同角度反映图像灰度信息,在图像边界提取上应用较为广泛。哈达玛变换节省了存储器的存储空间,有利于图像的快速运算。小波变换是空间(时间)和频率的局部变换,能从不同角度提取图像信息,从而为控制器处理图像提供了多种渠道。综上所述,不同的图像变换方式在图像处理中的应用各有不同,在纸张功能信息数字化的应用中发挥了各自的转换优势,为纸张功能信息数字化的图像处理提供了有力的理论和技术支持。
[1] Zhang Kaisheng, Li Zhijian, Zhang Xin. A digitalized encryption method based on raster graphic for paper fiber forming process: CN102747652A[P]. 2012. 张开生, 李志健, 张 馨. 一种纤维成纸过程的数字化加密方法: CN102747652A[P]. 2012.
[2] Zhang Kaisheng, Li Zhijian, Xu Yongjian. Discussion on Digitalization of Paper Fiber[J]. Przeglad Elektrotechniczny, 2012, 88(5b): 113. 张开生, 李志健, 徐永建. 纸张纤维数字化的探讨[J]. 电气评论, 2012, 88(5b): 113.
[3] Li Zhijian, Zhang Kaisheng. Study on the Digital Technology of the Papermaking Process[J]. Applied Mathematics & Information Sciences, 2014(5): 1. 李志健, 张开生. 造纸工艺数字化技术的研究[J]. 应用数学与信息科技, 2014(5): 1.
[4] TANG Wei, QIU Jin-qiang, LIU Qing-li, et al. The Application and Implementation of Triple Disc Refinier Control System Based on S7- 400PLC[J]. China Pulp & Paper, 2016, 35(5): 51. 汤 伟, 邱锦强, 刘庆立, 等. 基于S7- 400PLC的三盘磨浆机控制系统的应用与实现[J]. 中国造纸, 2016, 35(5): 51.
[5] HUANG Ya-nan, ZHANG Ai-juan, HU Mu-yi. The Research of Pulp Density Control Algorithm Based on Single Neuron PSD[J]. China Pulp & Paper, 2016, 35(5): 46. 黄亚南, 张爱娟, 胡慕伊. 基于单神经元PSD的纸浆浓度控制算法研究[J]. 中国造纸, 2016, 35(5): 46.
[6] Chen Hanqing, Wan Yanling, Wang Guogang. The research progress of digital picture processing technology[J]. Industrial Control Computer, 2013(1): 72. 陈汗青, 万艳玲, 王国刚. 数字图像处理技术研究进展[J]. 工业控制计算机, 2013(1): 72.
[7] Wang Hongwei. The general discussion about the application situation and development prospect of digital picture processing technology[J]. Printing Quality & Standardization, 2014(1): 51. 王红伟. 浅谈数字图像处理技术的应用现状与发展前景[J]. 印刷质量与标准化, 2014(1): 51.
[8] Zhu Wei. Feature-preserving image transformations in different domains[D]. Hangzhou: Zhejiang University, 2012. 朱 薇. 特征保持的图像变换研究[D]. 杭州: 浙江大学, 2012.

(责任编辑:刘振华)
Research on Paper Functionality Information Digitalization Based on Image Processing Techniques
ZHANG Kai-sheng1,2,*HOU Xin-gang1
(1.SchoolofControlEngineering,XijingUniversity,Xi’an,ShaanxiProvince, 710123; 2.CollegeofElectric&InformationEngineering,ShaanxiUniversityofScience&Technology,Xi’an,ShaanxiProvince, 710021)
This paper researched the image presentation of paper functionality digitalization with image processing techniques of Fourier transform, discrete cosine transform, Hadamard transform, Radon transform and wavelet transform. Through the research, the paper respectively pointed out the advantages of the image processing techniques aforementioned and provided solid theoretical and technical supports for the image process of paper functionality digitalization. Also, the viewpoints and methodologies in the paper provided the innovative mindsets for anti-counterfeiting of paper.
paper functionality; information digitization; image processing
张开生先生,教授;主要研究方向:大学生科技创新教育、控制理论与控制工程。
2016- 07- 07(修改稿)
TS7
A
10.11980/j.issn.0254- 508X.2016.11.003
(*E-mail: 80649433@qq.com)

