让算理与算法同行——《小数乘整数》教学设计与说明

张冬梅（特级教师）

【教学内容】

苏教版五年级上册第55～56页。

【教学重点、难点】

探索并掌握小数乘整数的计算方法。理解积的小数点的定位。

【教学准备】

教师：①软性小黑板3块；②课题；③遥控器。

学生：①每人一个计算器，②每人一份学习单。

【教学过程】

一、创设情境、引入新课

出示情境图1：

从图中，你获得了什么信息？

夏天，是西瓜丰收的季节，那么买3千克西瓜要多少元，怎么列式？

你是根据哪个数量关系式列式的？(单价×数量=总价)

二、主动探究，获得算法

1.学生探究0.8×3并交流算法。

0.8×3等于多少元呢？为什么？老师想把这个问题交给大家自己来研究。

请同学读一读研究提示：

想一想，0.8×3表示什么意思？

试一试，用我们已有的知识计算出结果。

写一写，记录下自己的方法。

说一说，在小组里交流自己的方法。

学生自主探究后，小组内交流，教师巡视。

全班分享，指名到前面介绍不同的方法。

预设：学生可能出现的方法有：

学生互动点评，点评要点：

方法（1）是根据 0.8×3表示3个0.8相加，把乘法转化成了加法；

方法（2）把小数乘法转化成了整数乘法；

方法（3）是先算 8×3。（如有学生提出为什么写竖式时3要与8对齐？那么就引导学生想：计算时是先看成多少乘多少的）

教师提问：这三种方法都正确吗？哪一种方法最简单呢？

那我们仔细来研究竖式计算的方法，我们先算8×3得24，那为什么结果是2.4呢？（引导学生讲0.8是8个十分之一，乘3，得24个十分之一）

大家可以结合这里的图来体会他们的说法。

动态演示3个0.8变成24个0.1的过程：

板书：8个十分之一，24个十分之一。

看来，0.8×3真的得 2.4元，集体口答：夏天买3千克西瓜要2.4元。

【说明：在应用已有的知识计算0.8×3的过程中，学生分别从乘法的意义、单位换算以及竖式计算的角度解决了问题，呈现出学生主动建构算法的精彩场景。而其中用竖式计算的方法是以前没有学过的，因此教师带着学生一起细究。在细究的过程中，教师注意了“算理直观”与“算法抽象”的有效联结，学生在动态的演示中，清晰地理清了为什么是先算8×3，而得到的是24个0.1，也就是2.4。学生在理解算理的基础上建构起了算法。】

2.尝试计算 2.35×3，进一步理解算理。

出示情境图2：

到了冬天，西瓜的单价发生了变化，还是买3千克，6元够吗？10元呢？

那么，到底需要多少元呢？让我们自己尝试着用竖式来算一算。

请一学生到前面板演。同学们完成后，请板演同学详细讲解计算过程，并互动质疑，弄清算理。

教师寻找学生的各种不同情况，展示并互动点评。

预设：（1）板演的同学讲计算过程，强调先算235×3；追问：为什么是两位小数呢？结合学生回答，板书：235个百分之一，705个百分之一。

（2）错误的。引导学生结合刚才的估算思考。

（3）如出现列竖式时出现小数点对齐的情况，引导学生思考：我们是先看成多少乘多少的。

个别同学订正后，集体口答：冬天买这3千克西瓜要7.05元。

【说明：在学生尝试计算前请学生先估算，不仅可以培养学生的数感，也可以帮助学生理解算理。而“尝试计算”也给了学生更大的学习空间与思考的自由，也让教师及时地发现学生各种不同的情况，以便学生在互动点评中共同提高。而在板演的学生详细讲解的过程中，学生讲到235×3得705时，教师恰当地喊出了“暂停”，让学生说一说，这时其实是算了多少乘多少？学生清楚地感受到了计算的步骤；教师接着又追问：那么结果为什么是7.05呢？一个问题指向算法，一个问题落实了算理，算法与算理始终并行。】

3.比较分析，获得算法。

完成了两个问题，我们得回头来看看。比较这两题，你发现什么相同的地方？

（1）都是小数乘整数。板书课题：小数乘整数。

（2）在竖式计算时，算法上有什么相同？都是先把它们当成整数乘法算，然后点小数点；

（3）观察乘数的小数位数和积的小数位数，你又有什么猜想？

照你们的猜想，你能在这几个竖式的积里点上小数点吗？

集体校对后，指出：

我们这样确定积的小数位数的方法正确吗？谁能说清这个“理”呢？我们还可以怎么证实呢？拿出计算器，检查一下结果是否正确。

讨论：小数和整数相乘，可以怎样计算？

【说明：两个问题解决后的静思与比较，让学生有了一些想法，而这些“想法”真的可行吗？教师引导学生既可以从算理的角度去分析，也可以用计算器去验证，多方考虑后学生获得了“小数乘整数”的算法。在这里，不仅培养了学生抽象概括的能力，也让学生经历到了数学推理的过程，亲身感受了数学的思想方法与科学精神。】

4.初用方法，促进内化。

（1）说说下面的算式先看成多少乘多少，再说说积分别是几位小数。

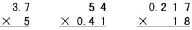
（2）如果我们想知道14.8×23的积，你只要知道哪道算式的积？

148×23=3404

14.8×23=

148×2.3=

追问：为什么不同的两题，积相同。

( )×()=34.04

【说明：抽象的方法具体化时，才更具有现实意义，因此教师在学生总结出算法后，及时让学生说说怎么算，怎么确定积的小数位数，也促进了算法的内化。而根据148×23＝3404，直接写出相关算式的积，教师改变了教材的呈现方式，而是从有利于培养学生逻辑思维能力出发，先出现 14.8×23，然后让学生“按图索骥”：你只要知道哪道算式的积？而“（）×（）＝34.04”又给了学生更开放的空间，学生的思维积极地展开了，高潮一个连着一个。】

三、拓展延伸

3.5×42，二千多年前的人们是怎么算的？

到底“算表”是怎么算这题的呢？“算表”能直接计算怎样的小数乘法么？一般的小数乘法，“算表”又是怎样解决的？我想，我已经无法阻挡大家的好奇了!那就让我们带着满满的收获与无限的好奇走出课堂吧！

【说明：课的最后介绍了有关“清华简”的内容，而到底当时的“算表”是怎么算的？课堂上没有交待，而也正因为如此，留给了学生无限的好奇，促进学生进一步的行动，主动地去寻找答案，这也正好表达了“促进学生41分钟发展”的理念。】