湿度传感器圆柱谐振腔辐射量的研究
张淑娥 孙丽红 孟宪盖
(华北电力大学电气与电子工程学院,保定 071003)
湿度传感器圆柱谐振腔辐射量的研究
张淑娥 孙丽红 孟宪盖
(华北电力大学电气与电子工程学院,保定 071003)
作为汽轮机里湿度传感器的圆柱谐振腔,以TE011模式工作.为了实时取样所测气体,在圆柱腔两个端面不同位置开多个圆环缝隙,产生了电磁场向外辐射,影响谐振腔的谐振特性及电磁环境.为了减少电磁辐射,研究电磁场从圆柱形谐振腔两端的圆环缝隙辐射的情况,谐振腔圆环缝隙的电磁场采用电磁场等价定理、边值条件及汉克尔变换,通过模式匹配推导缝隙结构的电磁场分布,给出了随不同开缝数量、位置、宽度及圆环厚度等结构参数的辐射情况.采用MATLAB数值计算圆环缝隙的辐射量;采用HFSS仿真圆环缝隙圆柱谐振腔,得到了圆环缝隙辐射量,仿真结果验证了理论方法的正确性.同时,给出了带有圆环缝隙的圆柱谐振腔作为湿度传感器的最佳结构参数.
湿度测量;圆柱谐振腔;圆环缝隙;辐射;模式匹配
DOI 10.13443/j.cjrs.2016030101
引 言
常规电站中大型冷凝式蒸汽透平的末几级和核电站中透平的全部级都在湿蒸汽状态下工作.蒸汽湿度的大小直接影响汽轮机运行的安全性和经济性,蒸汽湿度增加,一方面会对汽轮机叶片产生强烈的侵蚀与冲击,使叶片变得粗糙,出现凹坑,甚至造成叶片扭曲断裂,严重威胁汽轮机的安全运行;另一方面还会使汽轮机的热效率降低.因此,精确测定湿蒸汽的湿度对汽轮机的长期稳定性及其寿命具有重大意义.基于微波谐振腔的介质微扰法,通过谐振腔谐振频率的测量,可得到湿蒸汽的介电常数,进而确定蒸汽湿度.微波圆柱谐振腔作为湿度传感器是蒸汽湿度测量系统的关键部件,为了准确测量谐振腔谐振频率,选择圆柱谐振腔工作在品质因数很高的TE011模式.为了进行在线测量,微波圆柱谐振腔需开相对大面积的缝隙来采集湿蒸汽流,虽然圆环缝隙相比其他形状的缝隙能量辐射小,但缝隙的存在会产生一定的微波能量辐射,影响谐振腔的谐振特性.本文通过理论分析,得到圆环缝隙辐射量随数量、位置及厚度变化的解析式;从减小微波能量辐射角度设计圆环缝隙的最佳尺寸.
腔体缝隙产生电磁场辐射,在电磁场兼容和缝隙天线中有实际应用.研究缝隙辐射的有矩形缝隙辐射[1-2],圆孔缝隙辐射[3-6],圆环缝隙辐射[7-10]等.对矩形腔透过矩形缝隙的辐射采用时域有限差分方法[1]和模式匹配法[2]研究.对圆形空腔穿过单个圆孔采用有限元法/瞬时法[3],时域有限差分法[4]和模式匹配法[5]计算.对背腔多环(方位角对称的)缝隙辐射采用格林函数法、模式匹配法[6-8]等.缝隙天线通过开缝切割波导内壁表面电流而实现电磁场最大辐射,而本文研究圆柱腔体在谐振模式下最小电磁辐射的问题.
在对电磁场分析中,采用激励源等效首先将孔激励等效为腔体中央轴线的磁偶极子;使用格林函数法求得由激励源到腔体两端封闭时的场量;根据电磁场等价定理将被挖去的金属圆环电流等效为在两个区域的场量;模式匹配法给出缝隙区域的模式场量的表达式;由边界条件求出场量系数;由内向外,分析出从圆柱谐振腔,透过圆环缝隙的辐射能量解析式.最后采用MATLAB和HFSS仿真对比验证理论的正确性.
1 谐振腔的电磁场理论分析
1.1 激励源的确定
实际圆柱腔体两端开有多个缝隙,通过在腔体中间侧壁处开一椭圆孔,来实现激励,孔长轴方向与圆柱轴方向一致.通过孔的磁场激励,圆柱腔体内产生TE011模式的谐振波.由场等效理论,激励源可等效为圆柱腔体中央一磁流源,图1所示为圆柱谐振腔立体图.
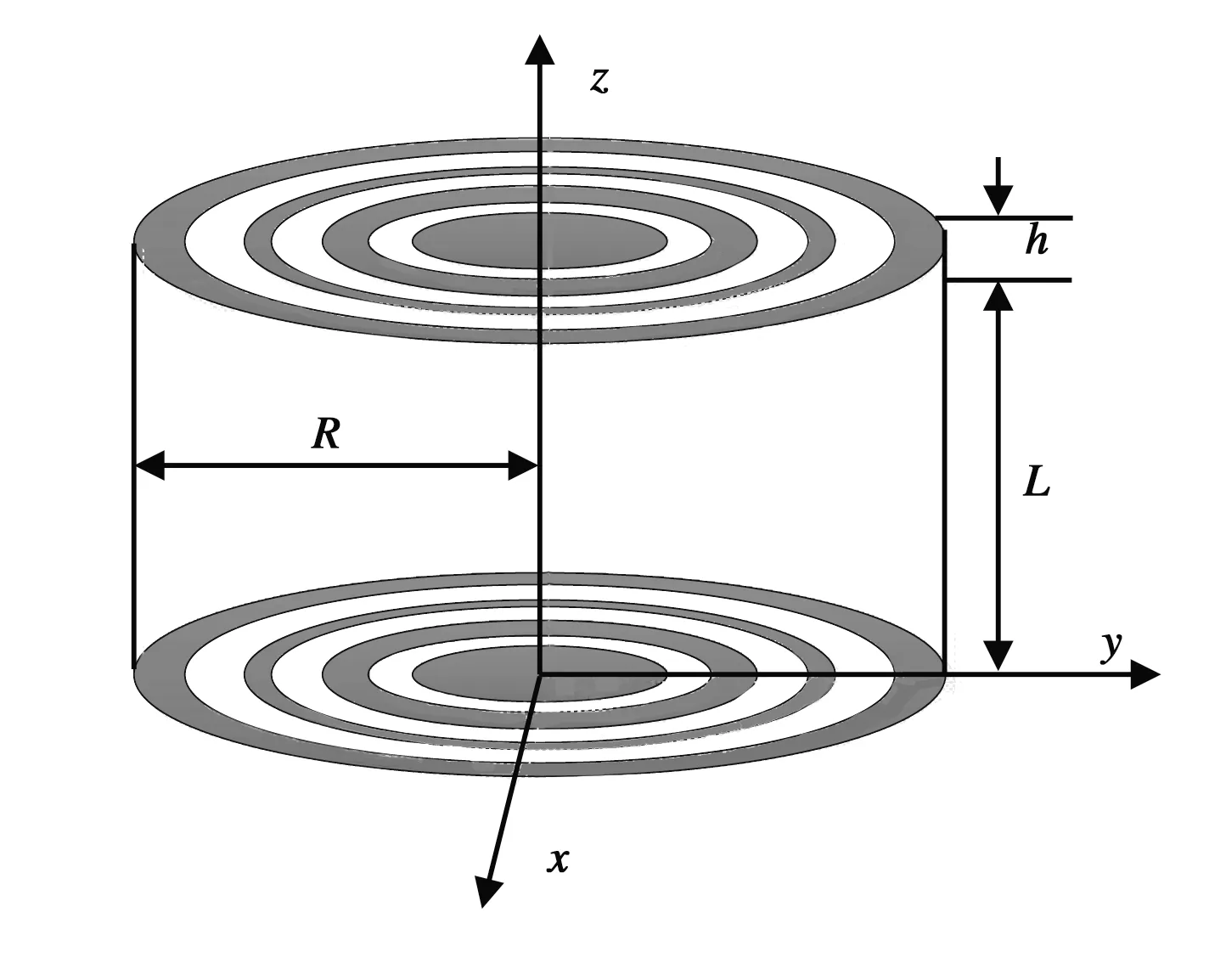
图1 圆柱谐振腔全局图
图2所示为圆柱谐振腔纵向剖视图.图2中,a为圆环缝隙的最小半径,w为缝隙宽度,T为相邻缝隙的间距,r为缝隙序号,h为缝隙厚度,R为谐振腔的内半径,L为谐振腔的高度.等效激励的磁流源Jm表达式为
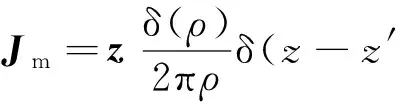
(1)
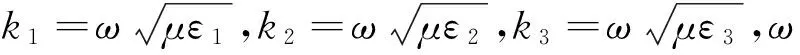
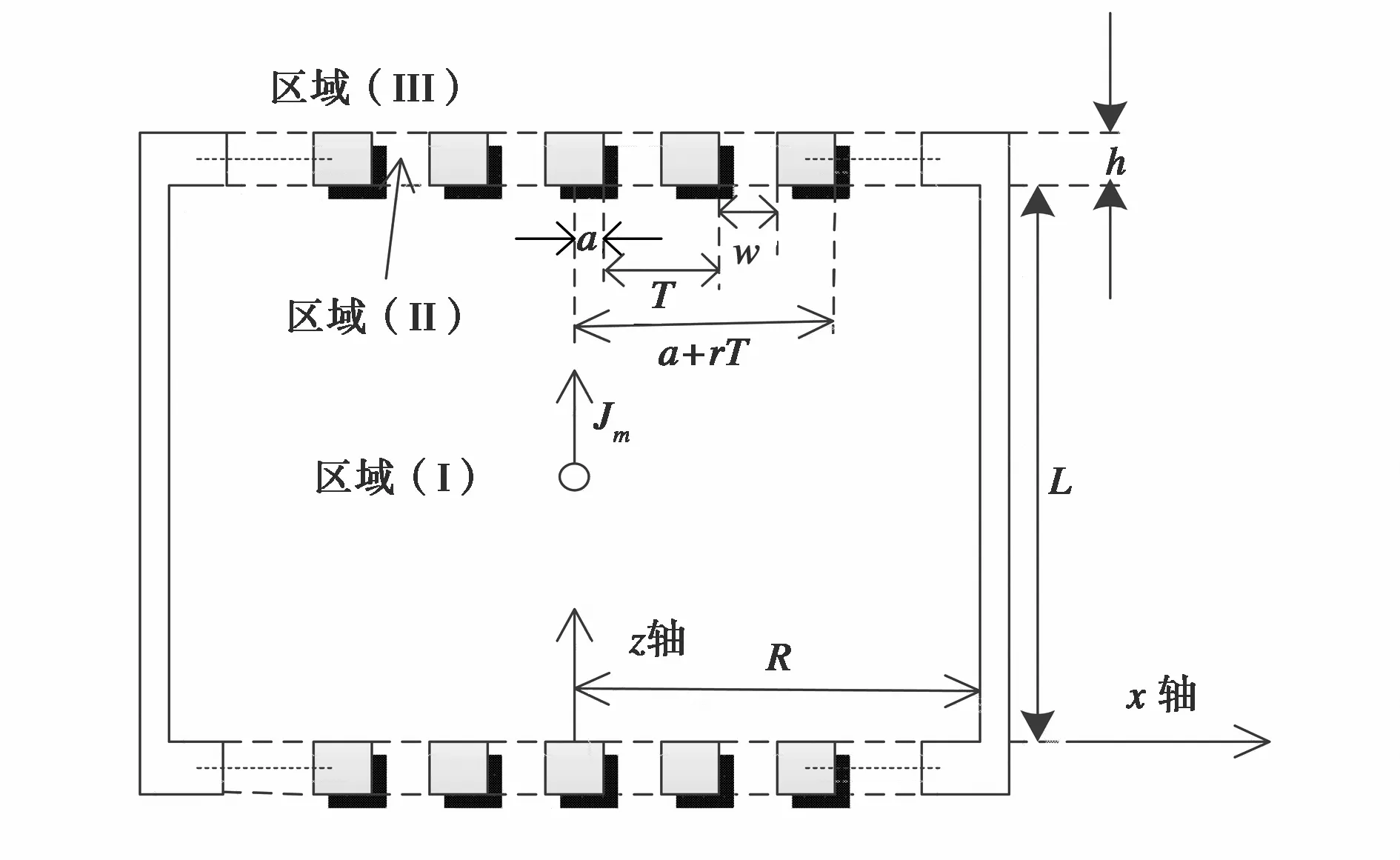
图2 圆柱谐振腔两端开圆环缝隙的剖视图
1.2 封闭谐振腔内电磁场的求解
将激励源等效为磁流激励,其满足的亥姆霍茨波动方程为
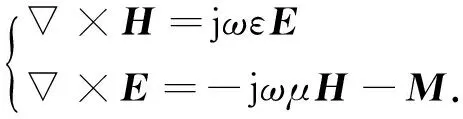
(2)
式中,M为磁流源.设F为电矢位,有
(3)
通过矢量运算,引入洛伦兹条件得到磁流源与电矢位的关系式:
(4)
这里M与式(1)的Jm相同.
应用格林函数法对电矢位求解,得到
[-N0(kρpR)J0(kρpρ)].
(5)
式中:J0(·)、N0(·)分别为0阶贝塞尔函数和纽曼函数,kρp为临界波数.利用电矢位F与场的关系,得到封闭谐振腔谐振磁场分量TE01p的解析式:
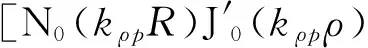
(6)
式中,上角标p代表区域I的主要电磁场量.只考虑p=1时, 式(6)为TE011模式的磁场分量.
2 圆环缝隙区域间场量的关系
由于腔体两端开缝结构是对称的,因此本文只对腔体一端的缝隙进行分析.
为了求解区域II中的电磁场,采用模式匹配法.设圆柱谐振腔两端的圆环缝隙,在区域I和II各产生新的带有待定系数的电磁场量.
首先分析区域I的电磁场.假设在区域I腔体内产生的等效谐振磁场分量为
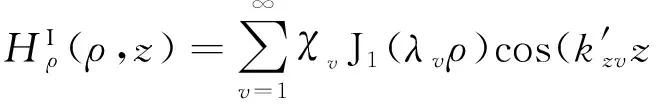
(7)

根据Hρ和Eφ的关系,由式(7),得到等效产生在腔体内的谐振电场分量为
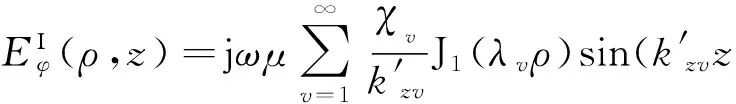
(8)
对区域II(圆环缝隙处)为同轴线结构,由波导模式激励知,同轴线的工作模式为同轴线的圆波导TE0n模式(n=1,2,3,…).根据传输线及波导理论,有
(9)
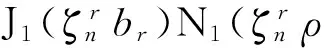
(10)
同理有:
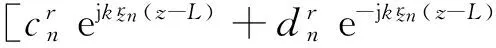
(11)
切向电场分量在z=L处满足多区域边界条件:
(12)
χv=

(13)
式中:
(14)
(15)
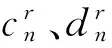
切向磁场分量Hρ在z=L边界处满足:
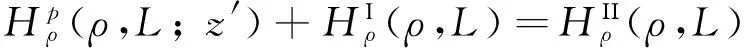
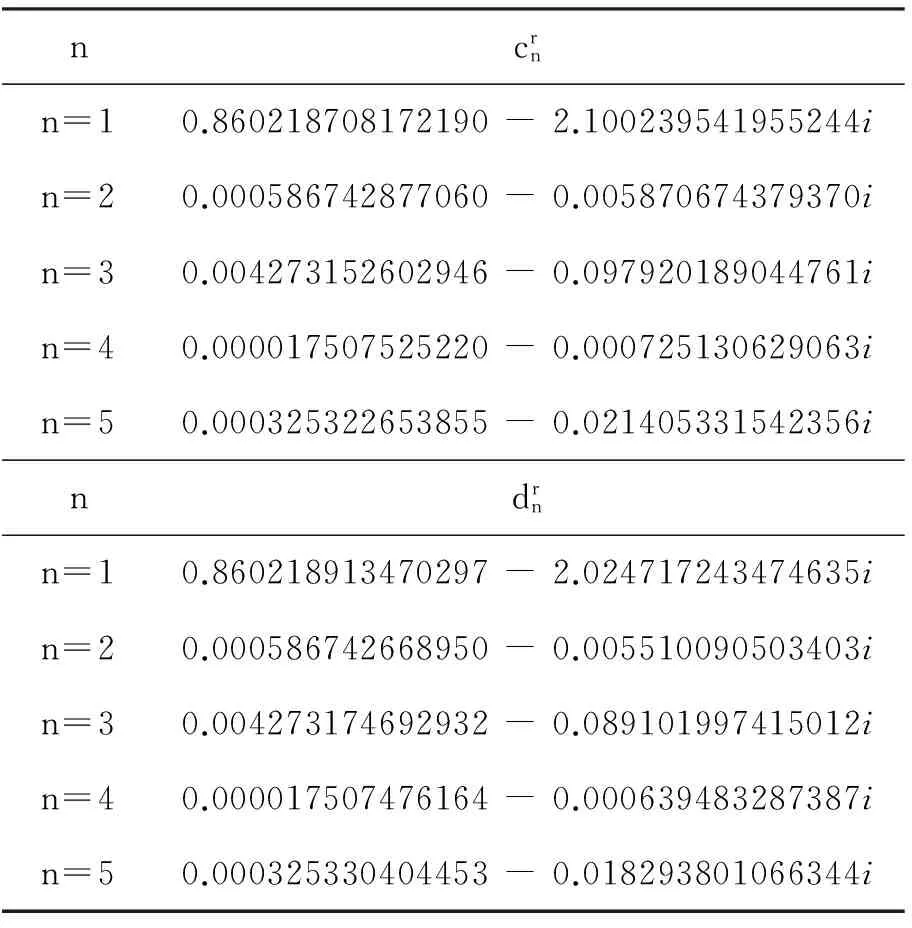
ar<ρ (16) (17) (18) 同样等式左边第二项有 (19) 式中, (20) 式(16)等式右边有 (21) (22) 为了求解圆环缝隙上表面辐射功率,需求出缝隙中的场量,同样需要考虑z=L+h 处的边界条件.切向电场Eφ在z=L+h满足 (23) Hρ磁场在III区满足汉克尔转换[10]: (24) 根据Hρ和Eφ的关系,由式(24)有 (25) (26) 同时,切向磁场在z=L+h处满足 (27) 等式左边有 (28) 等式右边有 (29) (30) 表1 待定系数随模式阶数的变化 n表示模式阶数,从表1看出,n增大,系数减小. 采用MATLAB对式(30)进行数值计算,得到的结果如图3所示.由图3可知:辐射量随缝隙位置的半径中心自内向外先增大后减小,在ρ=12 mm附近出现极大值;缝隙宽度越宽,辐射量越大. 采用HFSS仿真了圆柱谐振腔.采用矩形波导椭圆孔结构实现磁场激励.圆柱谐振腔工作模式为TE011,激励设计时,尽可能抑制掉TM111简并干扰模式.通过HFSS中的场计算器计算透过圆环缝隙的辐射量,得到的结果如图4所示.由图4可知:随着缝隙位置的半径中心从内向外,辐射量出现先增大后减小的趋势,在ρ=12 mm附近出现峰值;随着缝隙宽度变宽,辐射面增大,辐射量增大.MATLAB计算结果与HFSS仿真结果基本一致.本文数值计算1个数据点只用1 min左右时间,而HFSS仿真1个数据点需15 min左右时间,可见数值计算速度优势明显. 图4 HFSS仿真辐射量P随缝隙位置ρ变化曲线 以缝隙宽度4 mm为例,误差出现在ρ=12 mm附近,原因是存在干扰模式TM111与TE011同频谐振,采用HFSS仿真时,两个模式辐射能量叠加,造成HFSS仿真数据高于MATLAB计算数据. 根据上述辐射随缝隙尺寸变化的规律,设计了圆柱谐振腔两端面的四圆环结构,金属环尺寸: a1=5.2 mm,b1=5.8 mm;a2=9.2 mm,b2=12.6 mm;a3=14 mm,b3=15 mm;a4=19.1 mm,b4=20 mm. 改变金属环厚度,得到辐射量随缝隙厚度的变化规律,如图5所示. 图5 辐射量P随缝隙厚度h变化曲线 由图5可知,HFSS仿真数据略高于MATLAB数值计算数据,这是有TM111干扰模式存在的原因.辐射量从h=1 mm开始急剧衰减,说明腔体TE011谐振场在缝隙处是以“截止衰减”形式存在.但圆环开缝,包括缝隙厚度,同样影响干扰模式,造成干扰模式从缝隙辐射,即辐射量为TE011和TM111两者叠加的情况,从而造成辐射量随缝隙厚度在6.5~9 mm范围内“上升”.可见本文在求解TE011模式圆环缝隙辐射量时,数值计算的准确性优于HFSS仿真. 本文给出了一种分析两端带有圆环缝隙的圆柱谐振腔辐射量的分析方法:采用激励源等效理论,通过格林函数法得到两端封闭圆柱谐振腔的理想谐振模式TE011的场分量解析式;对腔体两端圆环开缝区域,采用电磁场等价定理,等价为腔体内和圆环缝隙两部分场量;通过模式匹配法,对缝隙内的场分量做模式分析,利用边界条件和汉克尔转换推得系数解.给出了穿过圆环缝隙表面辐射量的解析式.采用MATLAB数值计算该解析式,得到辐射量随腔体缝隙的半径、宽度及高度的变化规律,并与HFSS电磁仿真的数据对比,验证了理论分析的正确性.最后给出了设计的缝隙尺寸,为实际设计腔体提供数值依据. [1]OMIYA M, HIKAGE T, OHNO N, et al.Design of cavity backed slot antennasusing the finite difference time domain technique[J].IEEE transactions on antennas propagation, 1998, 46(12):1853-1858. [2]ZEONG J W, EOM H J.Radiation from cavity backed aperturesin a conducting plane[J].IEEE transactions on antennas propagation, 2005, 53(8):2761-2764. [3]REDDY C J, DESHPANDE M D, COCKRELL C R, et al.Radiation characteristics of cavity backed aperture antennas in finite ground plane using the hybrid FEM/MoM technique and geometrical theory of diffractio[J].IEEE transactions on antennas propagation, 1996, 44(10):1327-1333. [4]NAKANO H, SUGAMA M, NAKAYAMA K, et al.A circular aperture antenna backed by a cavity[C]//Proceeding of IEEE Antennas and Propagation Society International Symposium, 1999, 1:586-589. [5]PAEK J K, EOM H J.Cylindrical cavity-backed antenna[J].IEEE antennas wireless propagation letters, 2009, 8:852-855. [6]KIM J H, PARK Y B.Elecctromagnetic radiation from a circular cavity with circular apertures in a conducting plane[J].IEEE transaction on antennas and propagation, 2014, 62(9):4846-4851. [7]SHAFAI L, NOGHANIAN S.Analysis of dielectric-loaded annular slot array antenna[J].Electron computer engineering, 2003, 28(1):11-18. [8]KIM J H, EOM H J.Radiation from multiple annular slots on a circular cylindrical cavity[J].Electromagnetic waves application, 2007, 21(1):47-56. [9]KIM J H, EOM H J.Coaxially fed annular slot array antenna[J].IEEE transactions on antennas propagation, 2008, 56(2):590-592. [10]KIM J H, EOM H J.Scattering from an annular slot on a radial waveguide[J].Microwave optics technology letters, 2006, 48(2):354-357. 张淑娥 (1964-),女(满族),辽宁人,华北电力大学电子与通信工程系副教授,主要研究方向为微波技术及应用. 孙丽红 (1990-),女,河北人,硕士研究生,主要研究方向为微波技术及应用. Radiant quantitive study of cylindrical cavity for humidity measurement ZHANG Shue SUN Lihong MENG Xian’gai (SchoolofElectricalandElectronicEngineering,NorthChinaElectricPowerUniversity,Baoding071003,China) The cylindrical resonant cavity in steam turbine, as a wetness measurement sensor, works in TE011mode.Multiple annular slots are grooved at different positions on both ends of the cylindrical cavity to sample the wet steam in real time.The electromagnetic field radiates through these slots to the surroundings, influencing the resonant characteristics and electromagnetic environment of the resonant cavity.Research on the radiation from the annular slots at both ends of the cylindrical resonant cavity is valuable to reduce electromagnetic radiation.The electromagnetic field equivalence theorem, boundary value condition and Hankel transform were applied.The electromagnetic field distribution of the slots structure was derived by mode matching, and the radiation situations of different number, position, width, and thickness of annular were given.MATLAB was used to calculate the radiation of the annular slots, and HFSS simulation software was used to simulate the cylindrical resonant cavity with annular slots, and numerical results of radiation of the annular slots were obtained.The simulation results verify the correctness of the calculation method.The optimum structure parameters of cylindrical resonant cavity with annular slots as the wetness sensor is presented. humidity measurement;cylindrical cavity;annular slots;radiation;mode matching 张淑娥, 孙丽红, 孟宪盖.湿度传感器圆柱谐振腔辐射量的研究[J].电波科学学报,2016,31(5):962-968. 10.13443/j.cjors.2016030101 ZHANG S E,SUN L H, MENG X G.Radiant quantitive study of cylindrical cavity for humidity measurement [J].Chinese journal of radio science,2016,31(5):962-968.(in Chinese).DOI:10.13443/j.cjors.2016030101 2016-03-01 河北省自然科学基金(E2013502298) TK261 A 1005-0388(2016)05-0962-07 联系人:张淑娥 E-mail:zhang-shu-e@sina.com
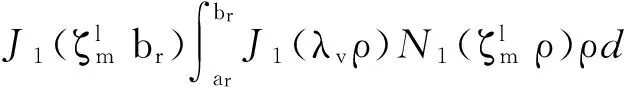
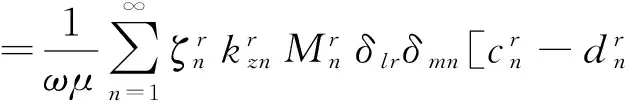
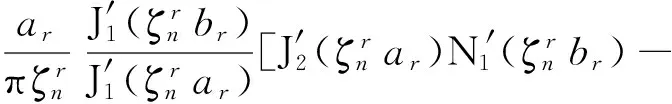
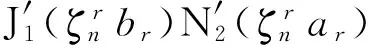
3 圆环缝隙上表面辐射功率分析
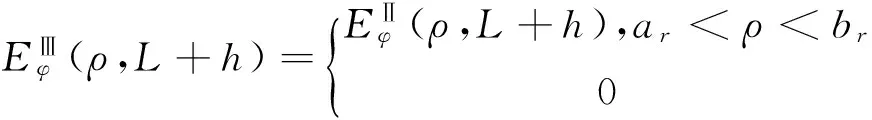
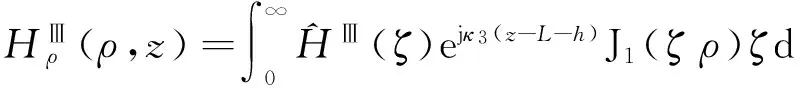
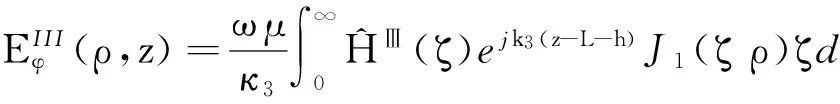
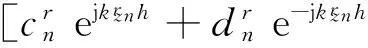
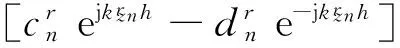
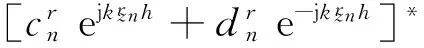
4 理论计算与HFSS仿真对比
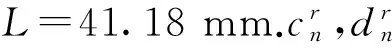


5 结 论



