嵌地线天线的辐射特性分析

廖飞龙 张东升 范启蒙 王刘军

(1.陆军军官学院,合肥 230031;2.电子工程学院,合肥 230031)



嵌地线天线的辐射特性分析

廖飞龙1张东升1范启蒙2王刘军1

(1.陆军军官学院,合肥 230031;2.电子工程学院,合肥 230031)

采用混合位积分方程结合矩量法对嵌地线天线进行了分析,讨论了Sommerfeld积分、阻抗矩阵元素及辐射场的计算等关键技术,仿真计算了嵌地线天线的辐射特性,并和FEKO软件的计算结果进行比对,验证了分析方法的正确性.与FEKO等电磁软件相比,文中方法在分析跨嵌电磁目标时,其计算效率具有明显的优势.

平面分层媒质;混合位积分方程;嵌地线天线;Sommerfeld积分;离散复镜像法

DOI 10.13443/j.cjors.2016061501

引 言

平面分层介质结构在单片微波与毫米波集成电路、微带天线、埋地及嵌地目标的电磁特性分析等领域中,具有广泛的应用．采用混合位积分方程[1]结合矩量法分析这类问题具有高效、准确等优点,因而一直为国内外学者所青睐．当前的研究中,对于电磁目标处于同一层媒质的情况讨论较多[2-6],而对于跨界面目标的电磁特性分析却较为少见[7-9],最主要的困难在于电磁目标跨界面时空域格林函数中所包含Sommerfeld积分的计算．平面分层媒质中Sommerfeld积分的计算,最主流的方法之一是离散复镜像法(Discrete Complex Image Method,DCIM)[10-11],它通常只对电磁目标处于同一层媒质时有效,当电磁目标处于不同层时,即跨层情况,Sommerfeld积分的计算往往需要进行繁琐的插值运算[9]．目前相当多的商用电磁软件仅有2.5维计算能力[12-14],只有IE3D、FEKO等少数软件能够进行全三维仿真,而IE3D、FEKO在计算空域格林函数时都采用数值积分和查表内插的方法,计算比较耗时．

本文首先根据混合位积分方程(Mixed-Potential Integral Equation,MPIE),结合矩量法,得到阻抗矩阵元素及其包含的谱域格林函数的表达式．然后分析阻抗矩阵元素计算的方法,并利用Formulation C[1]中标量位格林函数在分界面上对于场点纵坐标连续的性质,通过算子运算将对标量位格林函数的微分运算转移至表达式较为简单的电流基函数中,降低了矩阵元素计算的复杂性和计算量．在阻抗元素的计算中,对不同场源点位置情况下格林函数的计算采用了不同的方法,较好地解决了跨界面电磁目标分析中Sommerfeld积分计算困难的问题,然后推导了辐射场的计算,最后利用Matlab编程仿真了嵌地天线的相关电磁特性．

1 嵌地线天线的矩量法分析

1.1 阻抗矩阵的计算

平面分层媒质中(如图1所示),根据MPIE[1],第n层中任意点r′处电流源J(r′)在第m层中任意点r处产生的电场可以表示为

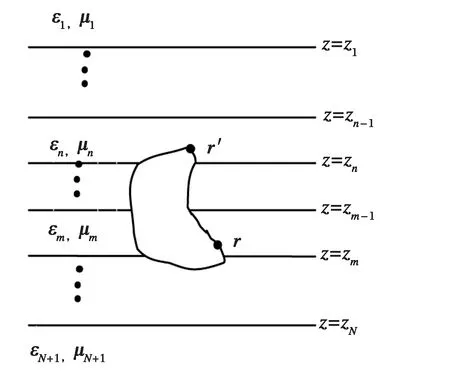
图1 平面分层媒质结构示意图

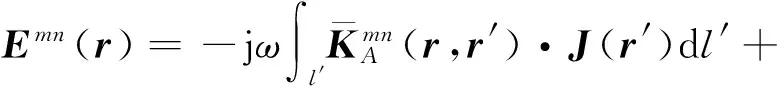
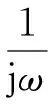
(1)

(2)

在矩量法中,阻抗矩阵元素的计算可以归结为源电流元产生的场和检验电流元的卷积运算,电流元Jn(r′)与Jm(r)之间的互阻抗元素按照MPIE可以表示为

Zmn=〈En(r′,r),Jm(r)〉

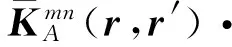
Jn(r′)·Jm(r)dl′dl+

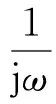
Jn(r′)·Jm(r)dl′dl.

(3)

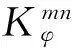
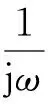
′·Jn(r′)dl′.

(4)

讨论式(4)中∫l[·Jm]dl积分部分,对于线天线,电流沿导线轴线方向一维分布,故梯度与散度的运算实际上就是一维求导运算,有

∫l.

(5)

对于第m模,如果上下半模处于同一层媒质,则

∫

(6)

如果第m模上下半模处于分界面的两侧,则

∫

(7)

这里利用了Formulation C中标量位格林函数在分界面处关于场点纵坐标连续的性质,即

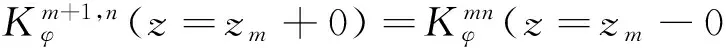
(8)

从式(6)和式(7)可以看出,无论第m模的上下半模处于同一层媒质,还是分别处于平面媒质分界面的两侧,都有

∫

(9)

所以式(3)的第二项积分可以写为

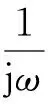
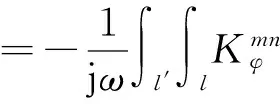
Jn(r′)dl·dl′.

(10)

式(10)无需对标量位格林函数进行微分运算,而将微分算子转移至表达式相对简单的电流基函数上,这将使计算量大大减小,并且此式对于电流基函数和检验函数具有较好的互易性,便于阻抗矩阵的优化计算．

综合前面的分析,阻抗元素的表达式可写为

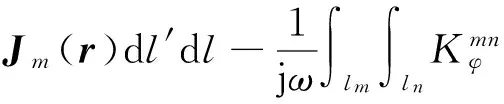
Jm(r)′·Jn(r′)dl′dl.

(11)

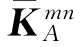
1.2 Sommerfeld积分的计算

(12)

求出积分的近似解析表达式．

对于嵌地线天线,源电流和检验电流所处的相对位置不同,其格林函数具有不同形式的表达式．在求取阻抗矩阵时,将Sommerfeld积分的计算分下面四种情况分别采用不同的方法．

1) 源电流和检验电流都在上半空间．阻抗元素计算过程中,场、源点均在上半空间,采用传统的二级DCIM[11]计算格林函数中所包含的Sommerfeld积分．

2) 源电流在下半空间,检验电流在上半空间．阻抗元素计算过程中,源点在下半空间,场点在上半空间,可采用二维离散复镜像法(2-Dimensional Discrete Complex Image Method,2D-DCIM)[15]计算格林函数中所包含的Sommerfeld积分,以避免繁琐的插值运算．

3) 源电流在上半空间,检验电流在下半空间．阻抗元素计算过程中,源点在上半空间,场点在下半空间,需要采用文献[16]提出的改进的二维DCIM计算格林函数中所包含的Sommerfeld积分,以避免介质的有耗特性给计算带来的错误．

4) 源电流和检验电流都在下半空间．场源点均在下半空间,如果下层媒质是无耗的,可采用传统的二级DCIM方法计算格林函数中所包含的Sommerfeld积分;如果下层媒质是有耗的,则需要采用文献[16]提出的改进的2D-DCIM方法计算位函数中所包含的Sommerfeld积分,以保证计算的准确性．

计算过程中,无论是采用传统的二级DCIM、2D-DCIM还是改进的2D-DCIM,如果电磁目标的电尺寸较大(lg(k0ρ)>1),都需要采用增强DCIM[17]的采样路径,以保证计算精度．

2 辐射场的计算

对于嵌地线天线的辐射场,根据实际工程情况,主要讨论天线在上半空间产生的辐射场,包括地上部分在上半空间产生的场和埋地部分在上半空间产生的场的总和．关于地上部分在上半空间产生的场,可通过文献[18]的方法直接得到,这里主要讨论埋地部分在上半空间产生的辐射场．

先计算远区磁矢位表达式．假设任意电偶极子的方向为(cos α,cos β,cos γ),其产生的磁矢位为

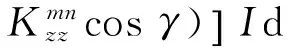
(13)

这里源点在下层,场点在上层,即m=1,n=2．下面计算矢量位各分量的近似表达式,由于z′≫z,可将关于z′的指数部分归为函数慢变部分,将其对积分的贡献归为驻相点的值从积分中提出[18],剩余部分用Sommerfeld恒等式得到即可．于是

(14)

分别计算A12(r)的各个分量,根据式(13)有

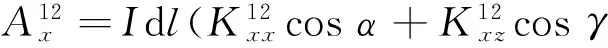
(15)

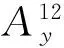
(16)

将地上部分和埋地部分产生的场相加可得总的辐射场．

3 数值计算

编程分析了如图2所示的λ天线,此天线架设在地面上空,两边用地钉固定,左端接地处用电压源馈电．在目前的实际工程中,都是将大地当成无限大理想金属导体板处理,也没有考虑地钉的作用,这样处理跟实际问题并不相符．本文将地面作为平面分层媒质,对地钉和天线一起进行剖分建模,展开矩量法分析计算．天线尺寸如图3所示,地钉长度为0.5 m,半径为0.005 m,天线的半径为0.015 m,地质相对介常数为εr2=4,地质电导率为σ2=0.001 S/m．

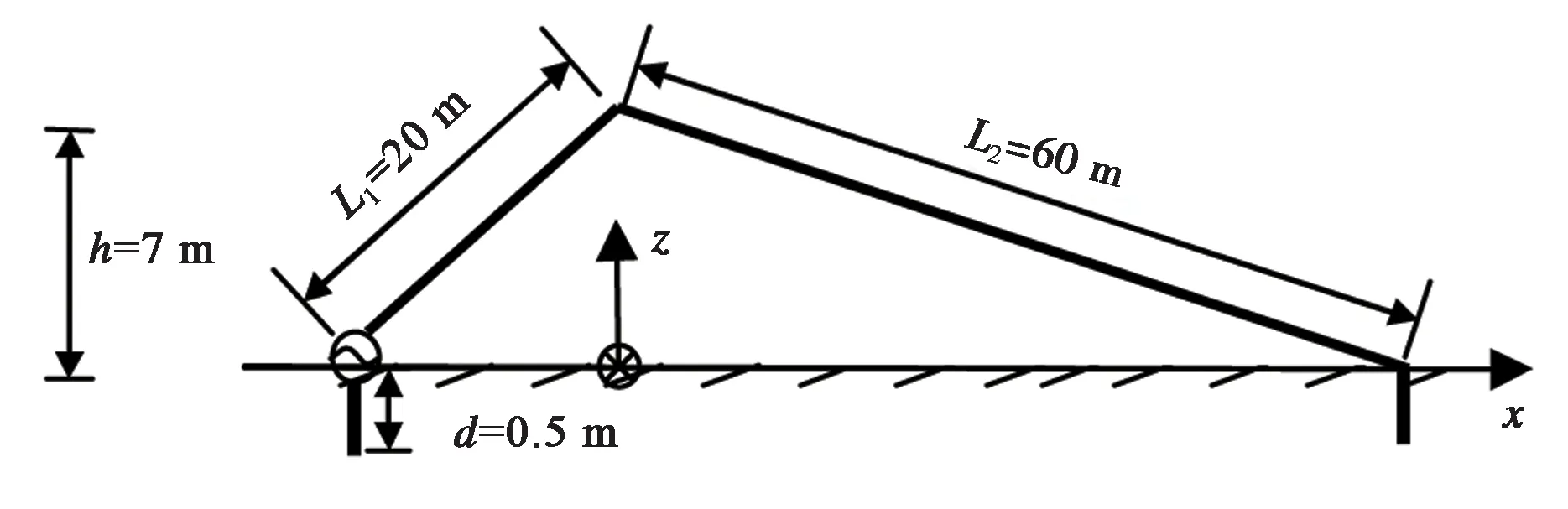
图2 λ天线架设示意图

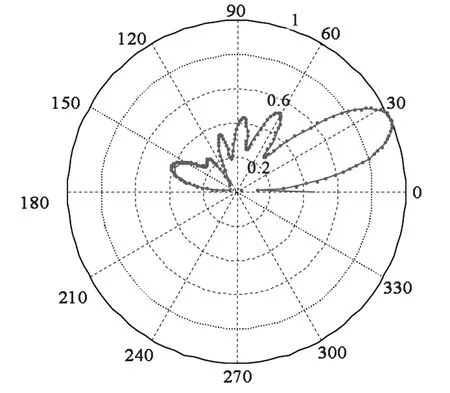
(a) E面方向图

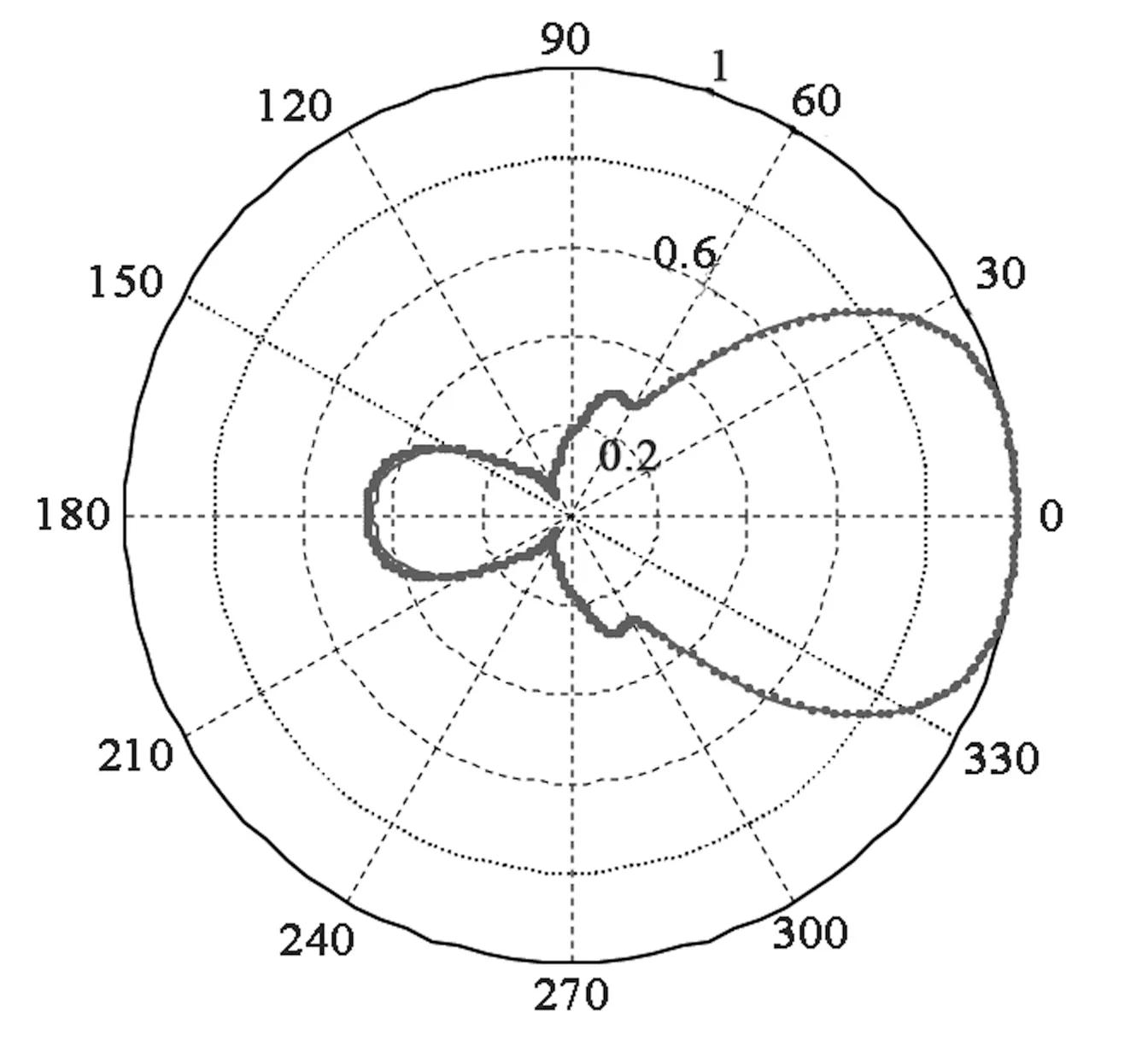
(b) H面方向图图3 天线的方向图

首先仿真了f=10 MHz时天线的方向图,并与FEKO软件的仿真结果进行了比对．从图3可以看出,本文方法计算结果与软件的结果吻合良好,证实了本文方法的正确性．

为了解地质参数对天线性能的影响,计算了天线在不同地质参数的方向图,如图4所示．天线工作频率f=10 MHz,地质相对介电常数为εr2=4,图4(a)表示φ=0°时,垂直平面内的方向图,图4(b)表示θ=90°时,水平面内的方向图．从图4可以看出,在保持其他参数不变时,地质参数的变化对天线方向图具有较大影响,并且随着地质电导率的增大,地质金属性增强,向上半空间反射的电场增大,从而使上半空间总的辐射场变大．

比较FEKO及本文方法的计算效率．天线工作频率为f=20 MHz,在Inter I5处理器、2G内存的计算机上,分别采用两种方法计算不同地质参数情况下天线的方向图,所用时间如表1所示．可以看出,随着地质电导率及相对介电常数的增加,FEKO计算时间急剧增加;而本文方法的计算时间基本稳定,并且天线电尺寸越大,结构越复杂,本文方法优势将越明显．这是因为FEKO在计算Sommerfeld积分时采用了数值积分的方法,每改变一次场源点位置都需要重新计算Sommerfeld积分的值,并且在地质电导率及相对介电常数变大的情况下,Sommerfeld积分的被积函数剧烈振荡,数值方法对其进行计算的时间就会急剧增加．而本文方法采用解析方法计算Sommerfeld积分,在一定地质条件下获得格林函数解析表达式以后,只要代入不同位置点的坐标即可得到不同位置坐标的格林函数,故计算稳定．

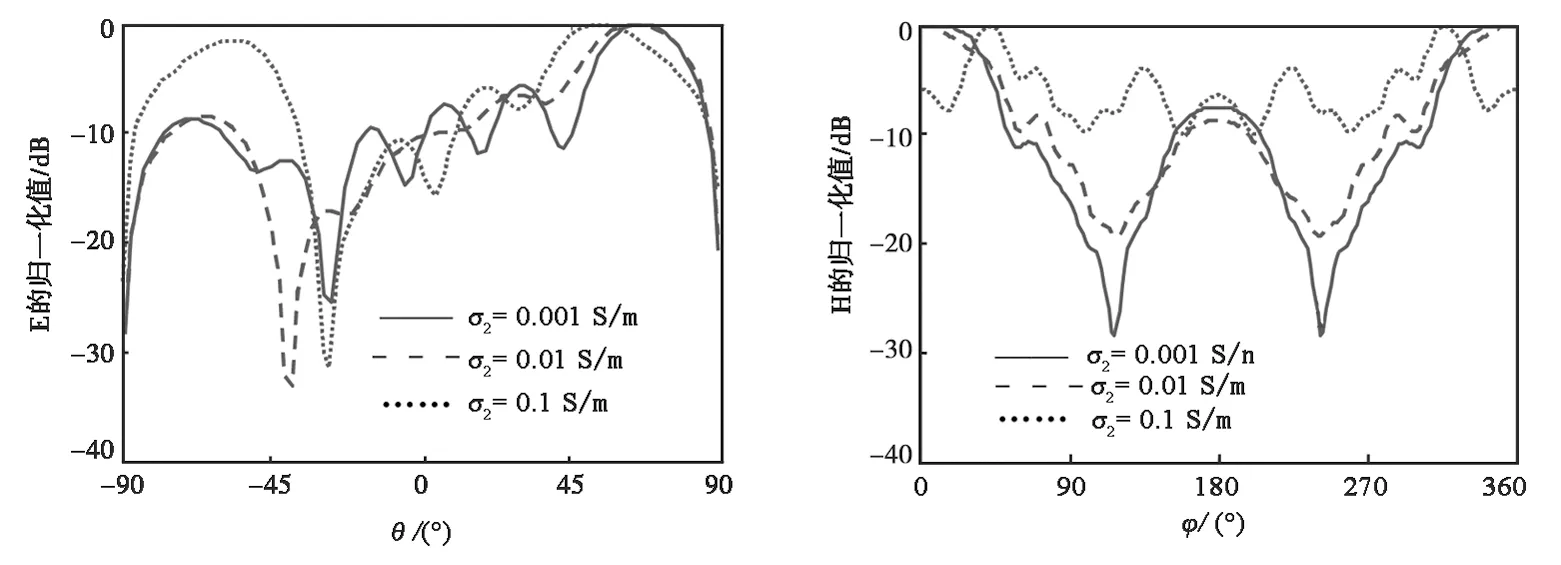
(a) E面方向图 (b) H面方向图图4 改变地质电导率时近地斜架λ天线的方向图

所用方法地质参数σ2=0.1S/mεr2=4σ2=0.01S/mεr2=4σ2=0.001S/mεr2=4σ2=0.001S/mεr2=20σ2=0.001S/mεr2=80FEKO339s61s32s496s1551s本文计算方法79s72s66s82s93s

4 结 论

跨嵌导体目标的电磁特性分析由来是分层媒质中电磁问题的难点,本文通过混合位积分方程结合矩量法分析嵌地线天线,仿真计算了天线的电磁辐射特性．从计算结果可以看出:地质参数的改变对于天线的电磁辐射特性具有较大影响,天线在架设使用时应充分考虑不同地面的影响;由于FEKO等电磁软件在处理跨层电磁目标问题时,对于Sommerfeld积分的计算多采用数值积分法,而本文采用解析的方法,在计算效率上具有明显的优势．为进一步提高嵌地线天线分析的效率,阻抗矩阵的优化计算将是后续研究的方向．

[1]MICHASKI K A, ZHENG D L.Electromagnetic scattering and radiation by surfaces of arbitrary shape in layered media, part I and part II [J].IEEE transactions on antennas and propagation, 1990, 38(3)：335-352.

[2]LEE J, ZOU J, J WAN, et al.Fast evaluating the electromagnetic fields generated by a vertical electric dipole over the lossy ground using Sommerfeld integral without truncation[J].IEEE transactions on electromagnetic compatibility, 2011, 53(4)：977-986.

[3]WU B Y, SHENG X Q.A complex image reduction technique using genetic algorithm for the MoM solution of half-space MPIE [J].IEEE transactions on antennas and propagation, 2015, 63(8)：3727-3731.

[4]SHOORY A, MOINI R, SADEGHI S H H.Direct use of discrete complex image method for evaluating electric field expressions in a lossy half space[J].IET microwave antennas propagation, 2010, 4(2)：258-268.

[5]于继军, 盛新庆.地下三维电磁散射的矩量法计算[J].电子与信息学报, 2006, 28(5)：950-954.

YU J J, SHENG X Q.Scattering from 3-D targets in the subsurface using MOM[J].Journal of electronics &information technology, 2006, 28(5)：950-954.(in Chinese)

[6]张云华, 肖伯勋, 朱国强.一种快速计算分层媒质中三维目标电磁散射的方法[J].武汉大学学报, 2007, 53(1)：119-122.

ZHANG Y H, XIAO B X, ZHU G Q.Fast evaluation of electromagnetic scattering from three dimensional objects buried in layered media[J].Journal of Wuhan University(natural science edition), 2007, 53(1)：119-122.(in Chinese)

[7]YE H X, JIN Y Q.Dual GPOF/DCIM for fast computation of Sommerfeld integrals and EM scattering from an object partially embedded in dielectric half-space[J].IEEE transactions on antennas and propagation, 2010, 58(5)：1801-1807.

[8]ARNAUTOVSKI-TOSEVA V, GRCEV L.Image and exact models of a vertical wire penetrating a two-layered earth[J].IEEE transactions on electromagnetic compatibility, 2011, 53(4)：968-976.

[9]LIU Y, LI L W, LEONG T S.Appliction of DCIM to MPIE-MOM analysis of 3-D PEC objects in multilayered media [J].IEEE transactions on antennas and propagation, 2002, 50(11)：157-162.

[10]FANG D G, YANG J J, DELISLE G Y.Discrete complex images for horizontal electric dipoles in a multilayered medium[J].IEE proceedings H-microwaves, antennas and propagation,1988, 135(5)：297-303.

[11]AKSUN M I.A robust approach for the derivation of closed-form Green’s function [J].IEEE transactions on microwave theory and techniques, 1996, 44(5)：651-658.

[12]TANG W H, GEDNEY S D..An efficient application of the discrete complex image method for quasi-3-D microwave circuits in layered media[J].IEEE transactions on microwave theory and techniques, 2007, 50(8)：1723-1729.

[13]尹成友.平面分层媒质空域Green函数快速计算(I) [J].微波学报, 2012, 28(2)：1-6.

YIN C Y.Fast computation of spatial Green’s functions for planar-layered media(I)[J].Journal of microwaves, 2012, 28(2)：1-6.(in Chinese)

[14]尹成友.平面分层媒质空域Green函数快速计算(Ⅱ)[J].微波学报, 2012, 28(3):1-8.

YIN C Y.Fast computation of spatial Green’s functions for planar-layered media(Ⅱ)[J].Journal of microwaves, 2012, 28(3)：1-8.(in Chinese)

[15]YUAN M T, ZHANG Y, DE A, et al.Two-dimensional discrete complex image method(DCIM) for closed-form Green’s function of arbitrary 3D structures in general multilayered media[J].IEEE transactions on antennas and propagation, 2008, 56(5)：1350-1356.

[16]廖飞龙, 尹成友, 杜红兵, 等.一种有效计算有耗分层媒质中的格林函数的方法[J].微波学报, 2010, 26(1)：27-32.

LIAO F L, YIN C Y, DU H B, et al.A robust approach for derivation of Green’s function for lossy layered media[J].Journal of microwaves, 2010, 26(1)：27-32.(in Chinese)

[17]YUAN M T, SARKAR T K, SALAZAR-PALAM M.A direct discrete complex image method from the closed-form Green’s functions in multilayered media [J].IEEE transactions on microwave theory and techniques, 2006, 54(3)：1025-1032.

[18]CHEW A W.A quick way to approximate a Sommerfeld-Weyl-type integral [J].IEEE transactions on antennas and propagation, 1988, 36(11)：1654-1657.

Radiation characteristics analysis of wire antenna partially embedded in the ground

LIAO Feilong1ZHANG Dongsheng1FAN Qimeng2WANG Liujun1

(1.ArmyOfficerAcademyofPLA,Hefei230031,China;2.ElectronicEngineeringInstituteofPLA,Hefei230031,China)

Mixed-potential integral equation (MPIE) combined with method of moment is used to analyze the wire antenna partially embedded in the ground.Some key techniques such as the calculation of Sommerfeld integrals, impedance matrix element and radiation field are discussed in this paper.Radiation characteristics of wire antennas partially embedded in the ground are calculated, and the results obtained are compared with that of the FEKO software, which confirms the correctness of this method.Compared with FEKO and other electromagnetic software, the approach presented in this paper has obvious advantages in computational efficiency for electromagnetic characteristics analysis of the object penetrating planar layered media.

plannar layered media;mixed-potential electric field integral equation;wire antenna partially embedded in the ground;Sommerfeld Integral;discrete complex image method

廖飞龙, 张东升, 范启蒙, 等.嵌地线天线的辐射特性分析[J].电波科学学报,2016,31(5):858-863.

10.13443/j.cjors.2016061501

LIAO F L, ZHANG D S, FAN Q M, et al.Radiation characteristics analysis of wire antenna partially embedded in the ground [J].China journal of radio science,2016,31(5):858-863.DOI：10.13443/j.cjors.2016061501

2016-06-15

安徽省自然科学基金项目(1408085QF121)

TN92

A

1005-0388(2016)05-0858-06

廖飞龙 (1981-),男,四川人,博士,讲师,主要研究方向为电磁数值计算、天线分析设计等．

张东升 (1968-),男,安徽人,副教授,硕士研究生导师,主要研究方向为无人机飞控技术等．

范启蒙 (1993-),男,河南人,硕士研究生,主要研究方向为电磁数值计算．

联系人：廖飞龙 E-mail：liaofeilong0514@163.com