二端口波混沌腔体短迹线随机耦合模型
李福林 韩继红 张畅
(1.解放军信息工程大学,郑州 450001;2.军队信息安全重点实验室,郑州 450001)
二端口波混沌腔体短迹线随机耦合模型
李福林1,2韩继红1,2张畅1
(1.解放军信息工程大学,郑州 450001;2.军队信息安全重点实验室,郑州 450001)
经典随机耦合模型在对电子设备的电磁脉冲效应进行预测时,边界条件设置在无穷远处,存在短迹线效应问题.采用设置辐射阻抗短迹线调制系数的方法,建立了二端口波混沌腔体短迹线随机耦合模型(Short-Orbit Random Coupling Model,SORCM),统计分析了目标点处感应电压的均方根误差随短迹线最大长度的变化关系.在不同的频段范围内,将SORCM计算结果的统计特性和实验结果进行了对比分析,验证了所建立模型的正确性.和经典随机耦合模型相比,SORCM的计算结果更加接近实测结果,可用于复杂电子设备电磁脉冲效应的预测和分析.
波混沌腔体;电磁脉冲效应;SORCM;辐射阻抗
DOI 10.13443/j.cjors.2016070501
引 言
随着电子技术的高速发展,大规模集成电路技术在各类电子设备中广泛应用,在提高电子设备处理能力的同时,也使得这些设备的电磁敏感度越来越高[1].超宽带(Ultra-Wideband, UWB)、高功率微波(High Power Microwave,HPM)等强电磁脉冲通过瞬态干扰、微波加温、高压击穿、电涌冲击等模式,造成电子元器件性能下降、状态反转、结点击穿、器件烧毁,妨碍电子设备的正常运行和作用发挥.开展电磁脉冲效应规律研究对于探索相应的防护措施、增强电子设备的生存能力具有重要意义.
由于电子设备内部结构的复杂性,其电磁脉冲效应问题较为复杂,难以用解析方法建立电动力学方程,运用时域有限差分(Finite Difference Time Domain,FDTD)法[2]、有限元法(Finite Element Method,FEM)[3]、矩量法(Method of Moments, MoM)[4]等数值计算方法求解需要耗费大量的计算资源,有时甚至无法求得问题的解.采用电磁拓扑法[5-7]将系统分解为多个子电磁空间,求解仍然十分复杂,且所建立的电磁拓扑模型与被分析个体紧密相关,难以推广到同类其他电子设备.采用传输线矩阵(Transmission Line Matrix,TLM)法[8]在对低频段的电磁干扰信号进行分析时行之有效,但当电磁波频率较高时,场的波动性明显增强,很难用集总参数进行有效的描述.
美国马里兰大学的Xing Zheng、Sameer Hemmady等人基于随机平面波假说和随机矩阵理论,提出了随机耦合模型(Random Coupling Model, RCM)[9-10],用统计学的方法对腔体内目标点的电磁效应物理量进行概率性的预测,对特定目标的研究结果可以给其他具有相似结构的系统提供参考,为复杂设备的电磁能量耦合分析提供了一种新的思路和方法[11].在国内,许多学者对RCM进行了研究和实验验证,闫二艳等人运用RCM对计算机机箱腔体内电磁效应物理量的统计特性进行了研究[12-13],庄信武等人总结了矩形、球形及其布尔组合体的混沌统计特性规律[14-15],陆希成等人基于天线辐射理论构建微波混沌腔的随机耦合模型[16],郝建红、范杰清、宋子贤等人运用RCM对一种调频发射电路目标点的电压概率密度进行了分析[17-19].
经典RCM在对辐射阻抗矩阵(radiation impedance matrix)的计算过程中,边界条件设置在无穷远处,等效于腔体侧壁边界为理想吸波材料,在这种情况下,没有任何反射波回到激励孔.但实际的电子设备内壁不会是理想的吸波材料,总有一些反射波会回到激励孔,这些反射波的轨迹被称为“短射线轨迹”(简称为短迹线,Short-orbit).由于短迹线效应的存在,经典RCM计算所得的目标点电压统计结果和实际测量统计结果的变化趋势基本一致,但二者的峰值有偏差.文献[12]在对经典RCM进行实验验证时,发现存在短迹线效应问题,但未给出解决该问题的方法.文献[14]提出了短迹线耦合技术,但未给出详细的解决方案,且未针对具体的混沌腔体开展实验验证.文献[20-23]只对腔体内单目标点的短迹线效应问题进行了研究,且未给出目标点感应电压统计分析的具体结果.用统计的方法对混沌腔体内的电磁效应物理量实施建模,其精度与射线轨迹是否充分遍历整个混沌腔体有关.解决短迹线效应问题的关键是分析短迹线属性与电磁效应物理量的关系,本文通过定义辐射阻抗短迹线调制系数的方法建立了辐射阻抗和短迹线属性的关系,给出了辐射阻抗短迹线调制系数的计算方法,并对该方法在二端口波混沌腔体条件下进行了实验验证.
1 理论分析
1.1 随机耦合模型
经典RCM指出:对于复杂的波混沌腔体,其内部电磁参量可以分为通用统计特性和非通用统计特性两部分,对于二端口有损金属腔体,用Zcav表示其腔体阻抗矩阵,则Zcav可由式(1)进行描述[9-10]:
(1)
式中:Zrad代表腔体的自由空间辐射阻抗;Znor代表腔体的归一化阻抗.
腔体的自由空间辐射阻抗Zrad可由式(2)得出:
(2)
式中:Z0为实对角矩阵,其元素为连接激励孔传输线的特征阻抗;I2×2为2×2的单位矩阵;Srad为腔体的辐射散射系数,可通过电磁仿真软件或直接测量获得.
腔体的归一化阻抗Znor可由式(3)得出:
(3)
式中:W是一个2×M的耦合矩阵, M为二端口波混沌腔体的模数,元素Wij描述第i个激励源与腔体第j个本征模之间的耦合,Wij是满足方差为1、均值为0的独立高斯分布的随机数;WT代表W的转置矩阵;P为M×M的对角矩阵,其目的是产生M个特征值,这些特征值满足Wigner半圆分布;I为M×M的单位矩阵;α为腔体损耗因子,可由公式法或直接比较法求得[19].
1.2 二端口波混沌腔体短迹线随机耦合模型
经典RCM在使用式(2)计算腔体辐射阻抗Zrad时,将腔体侧壁边界等效为理想吸波材料,未考虑实际电子设备存在的短迹线轨迹.为建立电磁效应物理量和短迹线属性的关系.定义辐射阻抗Zrad的短迹线调制系数ξ=ρ+jx,存在短迹线时的辐射阻抗用Zsoc表示,则有
(4)
Zsoc的实部和Zrad的实部满足
(5)
Zsoc的虚部和Zrad的虚部满足
(6)
考虑短迹线效应后,计算腔体阻抗的式(1)可用式(7)表示:
(7)
式(4)~(7)称为波混沌腔体短迹线随机耦合模型(Short-orbit Random Coupling Model, SORCM).
下面推导准二维波混沌腔体辐射阻抗短迹线调制系数ξ的解析表达式.定义如图1所示的准二维波混沌腔体,高度h远小于入射波长,假设电场只沿z方向传播.

图1 准二维腔体截面
由经典RCM,端口m和n之间的阻抗可表示为
Zm,n=
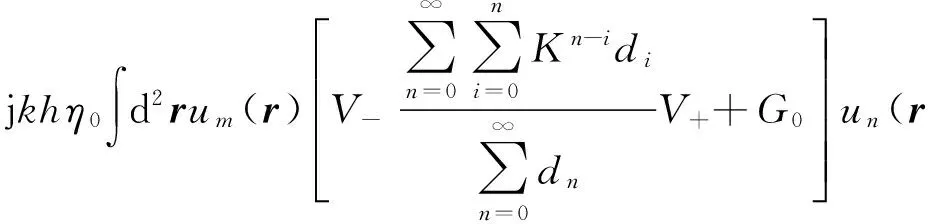
(8)
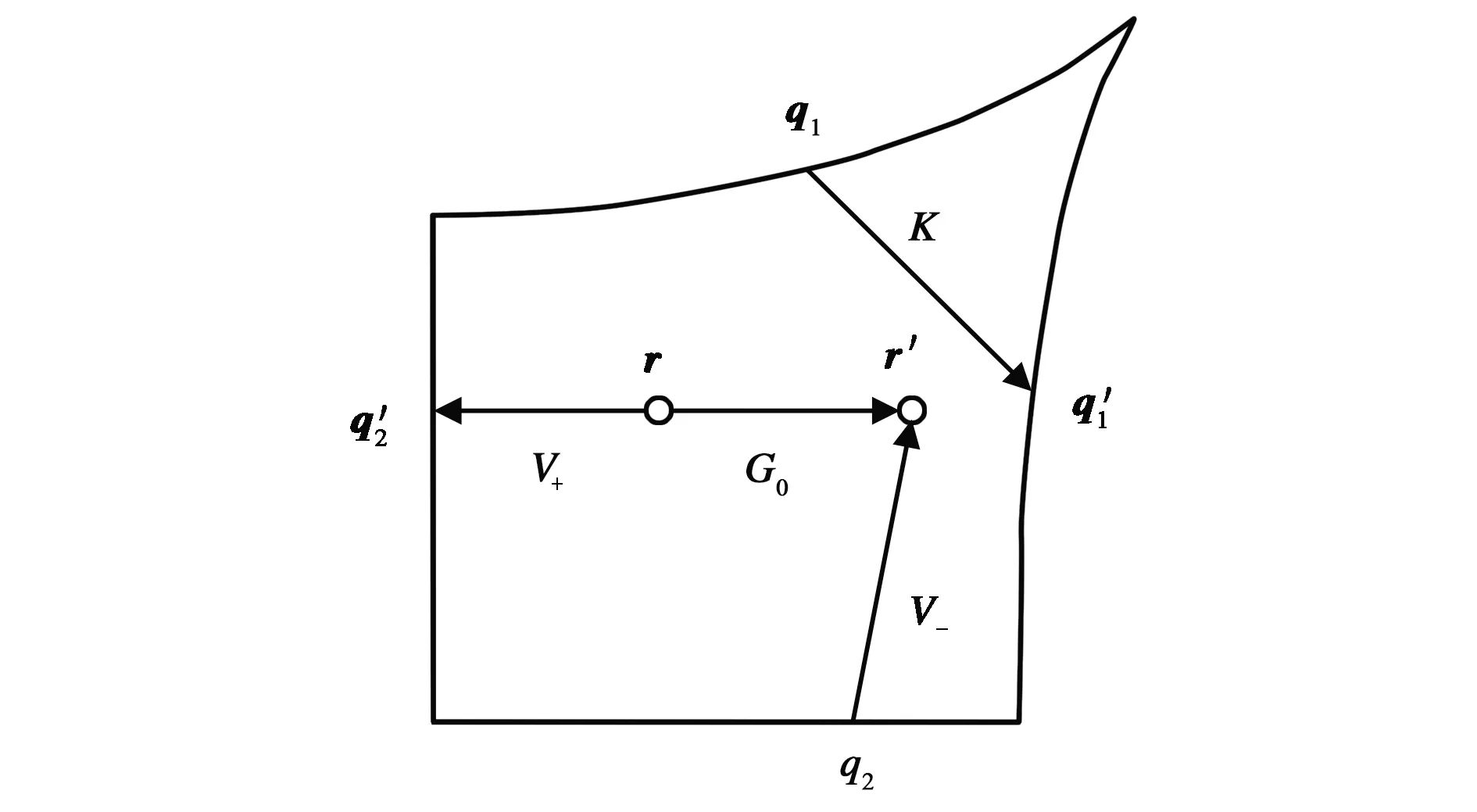
图2 运算符V-、V+、K、G0示意图
为考虑RCM的短迹线效应,定义M×M的矩阵Z,其元素为Zm,n由式(9)表示:
Zm,n=jkhη∫d2rum(r)G0un(r),
(9)

(10)
式(10)中的各个子项满足式(11)~(13):
(11)
=khη∫∫d2run(r)[V-(K)β-1V+]um(r);
(12)
(13)
式(11)中,θ为迹线的反弹入射角,矩阵θ为
θ=[cos(θ),sin(θ)].
(14)
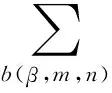
式(13)中的Db(β,m,n)表示迹线b(β,m,n)的稳定系数,为
(15)
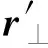
由式(9)~(15)可得在腔体有损耗的情况下,端口m和n之间的短迹线调制系数为
(16)
式中:Lb(β,m,n)为迹线b(β,m,n)的长度,设其最大值为LM;Lp(β,m,n)为端口m和端口n之间的距离;k′=k/(2Q)为有效衰减参数,Q为腔体的品质因子;pb(β,m,n)是迹线b(β,m,n)在系综中出现的概率.
将式(16)代入式(4)后,再将式(4)代入式(7),即可得到考虑短迹线情况下腔体阻抗的计算公式.
2 实验过程与结果分析
以某电子设备作为实验箱体,其长、宽、高尺寸分别为48.2 cm、45.0 cm、17.8 cm.以箱体的右下外侧顶点为原点建立坐标系,如图3所示,孔1位于坐标(0,22.5,8.9)处,取三个目标点A、B、C分别位于坐标(24.1,22.5,8.9)、(36.2,22.5,8.9)、(36.2,11.5,4.5)处.
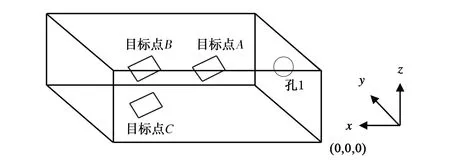
图3 实验箱体模型
2.1 实验环境与实验过程
2.1.1 腔体散射矩阵的测量
腔体散射矩阵的测量环境如图4所示.
为加强射线的混沌特性,基于“模式搅拌理论”,在腔体内部放置一个模式搅拌桨,该桨由一个直径为2 cm的圆柱体和三个间隔为5 cm、尺寸为6 cm×3 cm的叶片组成.在孔1和目标点之间连接矢量网络分析仪,在频率范围为4.9~5.1 GHz和5.9~6.1 GHz两个频段内,采取模式搅拌的方法,每隔1 MHz为一个采样点,每10°旋转一次搅拌桨,共旋转2周,对每个目标点,都可以获取腔体散射矩阵2×200×72的系综实验数据.
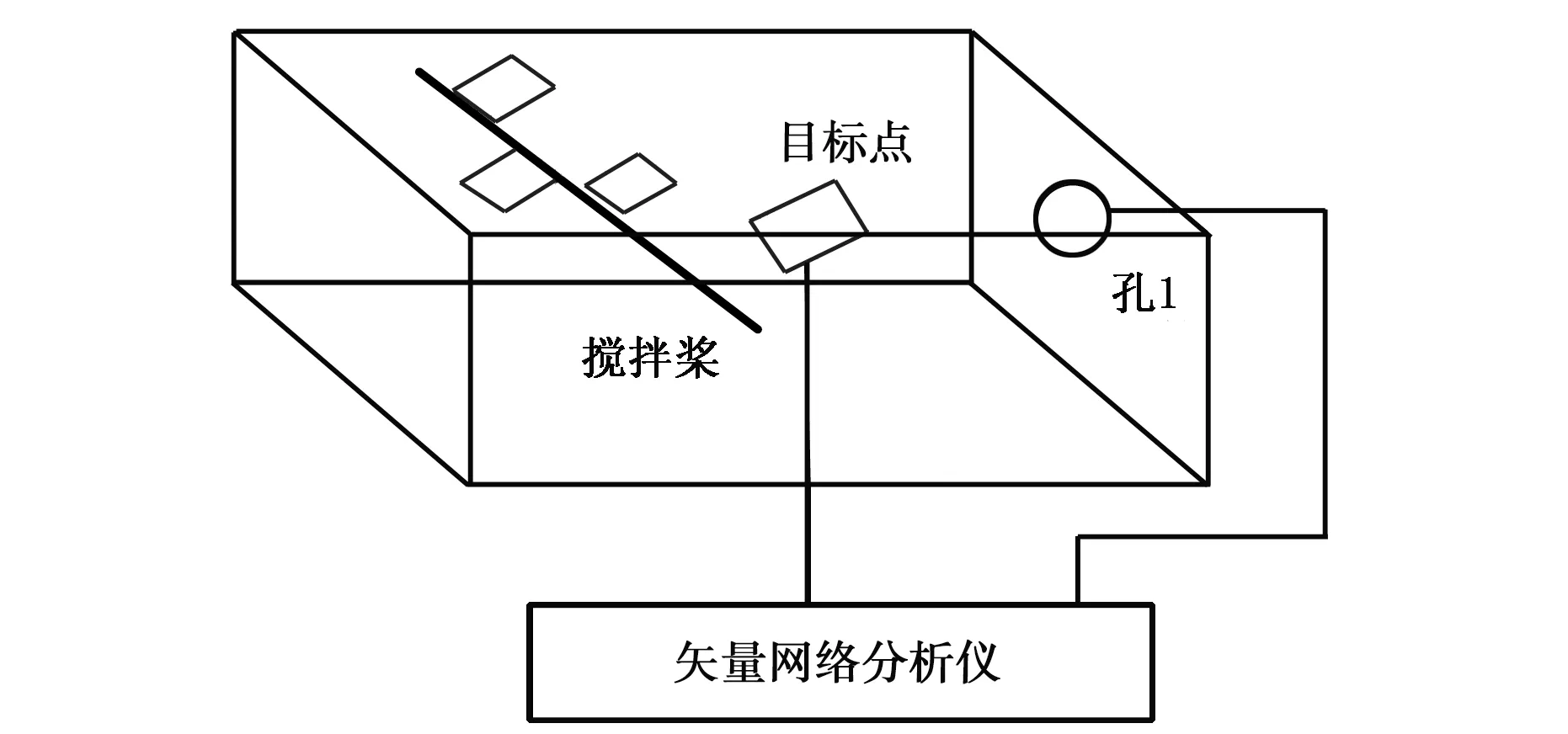
图4 散射矩阵测量环境示意图
2.1.2 腔体辐射散射矩阵的测量
腔体辐射散射矩阵是激励进入腔体后没有反射情况下的散射矩阵,因此在测量辐射散射矩阵时,将图4中实验腔体的内壁覆盖吸波材料,移除搅拌桨,在同样的频段内,每隔1 MHz为一个采样点,在不同的时间、相同的实验条件下做30次测量,对每个目标点,获取腔体辐射散射矩阵2×200×30的系综实验数据.
2.1.3 目标点感应电压的测量
断开图4中矢量网络分析仪和实验箱体的连接,激励孔1连接信号发生器和功率放大器,目标点连接示波器,在同样的频段内,采用同样的频点采样方法和模式搅拌方法,通过示波器获取每个目标点感应电压2×200×72的系综实验数据.
2.2 目标点感应电压计算方法
结合微波双端口网络中阻抗参量的概念,在分别考察每个目标点的感应电压时,可将图3所示的腔体结构抽象为如图5所示的双端口微波网络.
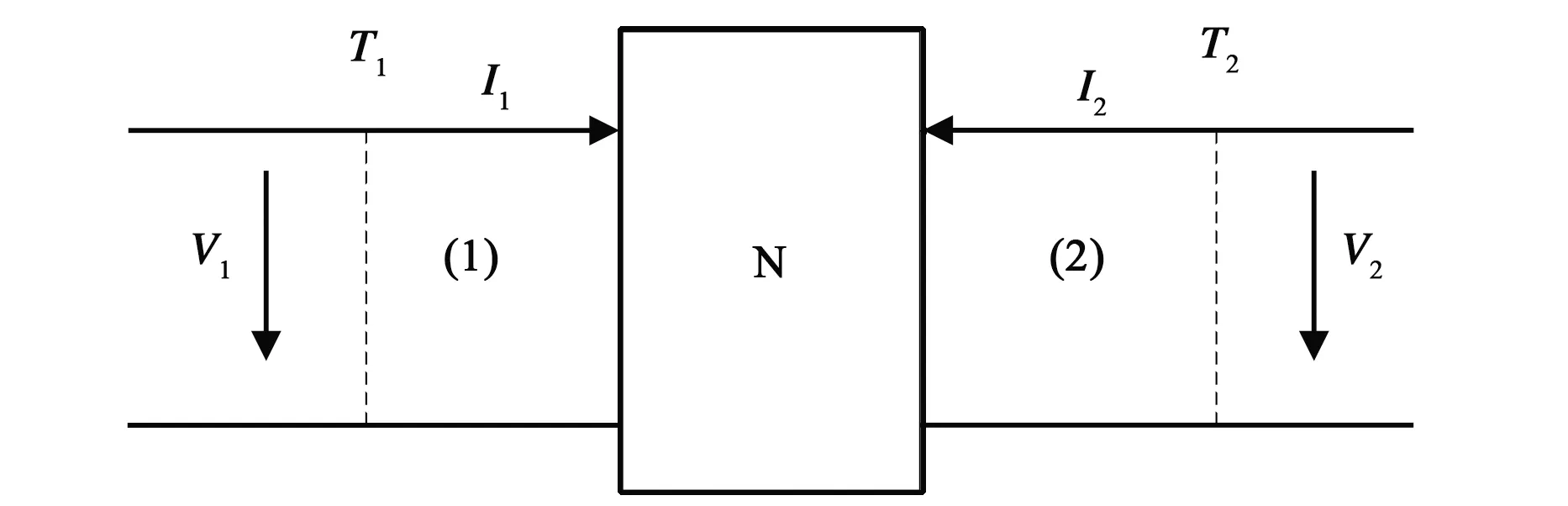
图5 双端口微波网络等效电压、电流示意图
对图5所示的双端口微波网络,等效电压、电流与阻抗的关系可表示为
(17)
腔体阻抗可表示为一个2×2矩阵:
(18)
在目标点开路的情况下,可由孔1的辐射功率频谱分布求得目标点处感应电压V2的统计分布:
(19)
式中,P1(f)为孔1处激励信号的功率密度分布函数.
2.3 短迹线最大长度确定方法
短迹线长度的含义是“从电磁波进入腔体,经若干次反射,直至其离开腔体所经过路径长度的总和”[23],理论上短迹线最大长度的取值范围为(0,+∞),短迹线最大长度的取值越大,式(16)计算时所包含的短迹线数目也就越多,SORCM的计算结果越准确,但相应的计算时间也就越长.在工程应用中,需要结合实际,确定一个短迹线最大长度的门限值.
文章通过分析目标点感应电压的均方根误差随短迹线最大长度变化关系的方法,来确定满足要求的短迹线最大长度门限值.定义目标点处感应电压V2的均方根误差eRMS为
(20)
式中:n为样本总数;〈Vi〉为Vi的平均值.
目标点处感应电压V2的eRMS随短迹线最大长度LM的变化情况如图6所示.
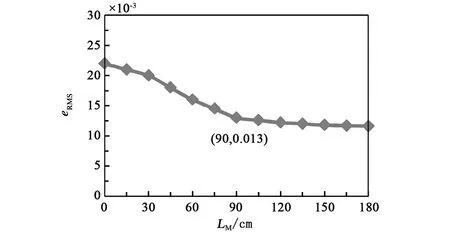
图6 eRMS随短迹线最大长度的变化情况
工程应用中要求目标点处感应电压的均方根误差小于0.013,从图6可以看出,当eRMS的取值为0.013时,对应的LM值为90 cm.当LM的取值大于90 cm时,可以满足均方根误差小于0.013的要求.为简化计算量,在本文的实验条件下,选择LM为90 cm.
2.4 短迹线随机耦合模型计算结果分析
对如图3所示的腔体,对目标点A,采用2.1节的实验方法,注入功率P1(f)=1 W,Lp(1,2)=24.1 cm,由2.3节的分析,选择短迹线的最大长度LM为90 cm,采用随机矩阵蒙特卡罗法[18]确定腔体的损耗因子α,分别采用经典RCM的式(1)、短迹线随机耦合模型SORCM的式(7)计算腔体阻抗,由式(19)计算目标点的感应电压V2在两种模型下的统计分布.
经典RCM、SORCM和实验测量统计结果的对比情况如图7、8所示.
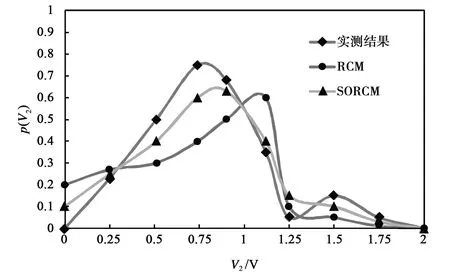
图7 4.9~5.1 GHz目标点A感应电压统计分布
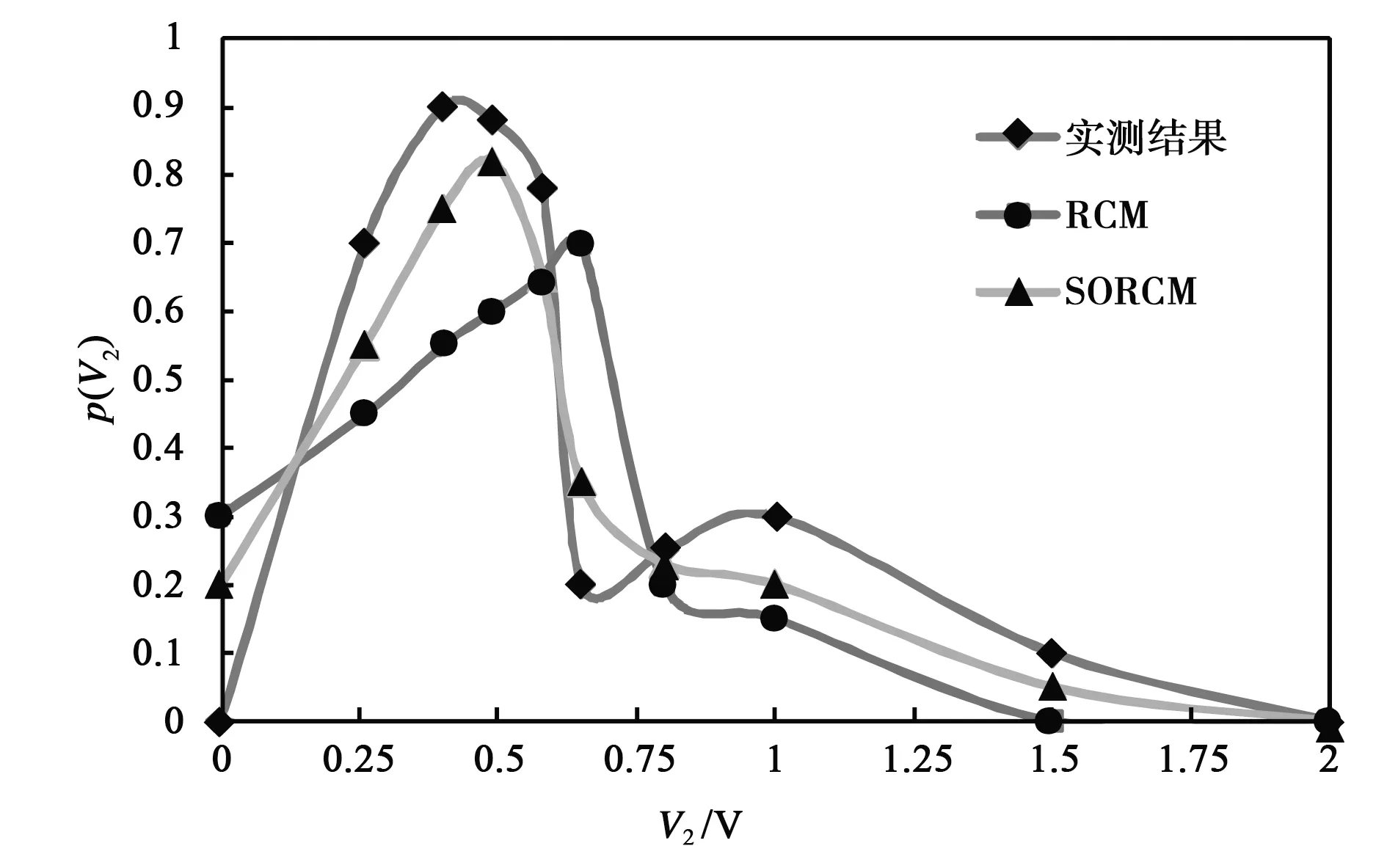
图8 5.9~6.1 GHz目标点A感应电压统计分布
从图7可以看出,在4.9~5.1 GHz频段范围内,实测结果、经典RCM计算结果、SORCM计算结果得到的目标点A处感应电压值的最大概率分别出现在0.74 V、1.12 V和0.90 V.经典RCM在对辐射阻抗的计算过程中,边界条件设置在无穷远处,等效为腔体侧壁为理想吸波材料,所有进入腔体的电磁波都被设备充分吸收,因此和SORCM相比,计算结果偏大,而SORCM考虑了散射系统的短迹线属性,计算结果更加接近实测值.从图8可以看出,在5.9~6.1 GHz频段范围内,实测结果、经典RCM计算结果、SORCM计算结果得到的目标点A处感应电压值的最大概率分别出现在0.40 V、0.65 V和0.49 V,同样,SORCM的计算结果更加接近实测结果.对目标点B和目标点C的实验结果进行统计分析,可以得出与目标点A一致的结论.
在实验的频段范围内采用SORCM方法分别计算目标点A、B和C感应电压的概率密度,结果如图9、10所示.
比较图9和图10中三个目标点概率最大的感应电压值,可以看出:在4.9~5.1 GHz频段范围内,目标点A最大,为0.90 V,其次是目标点B,为0.74 V,目标点C最小,为0.51 V;在5.9~6.1 GHz频段范围内,同样是目标点A最大,为0.49 V,其次是目标点B,为0.40 V,目标点C最小,为0.26 V.其原因是目标点A离激励孔最近,耦合的能量最大,其次是目标点B,而目标点C距激励孔最远,耦合的能量最小.
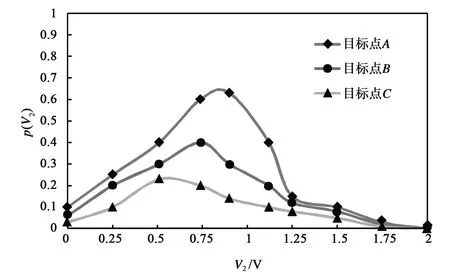
图9 4.9~5.1 GHz目标点感应电压SORCM计算结果

图10 5.9~6.1 GHz目标点感应电压SORCM计算结果
3 结 论
通过定义辐射阻抗短迹线调制系数的方法,在4.9~5.1 GHz和5.9~6.1 GHz两个频段范围内,建立了二端口波混沌腔体短迹线随机耦合模型,统计分析了目标点处感应电压的均方根误差随短迹线最大长度的变化关系,对建立的二端口短迹线随机耦合模型进行了实验验证.结果表明,与经典随机耦合模型相比,短迹线随机耦合模型的计算结果更加接近实测结果,能够更有效地预测复杂电子设备的电磁脉冲效应.论文的研究可进一步促进随机耦合模型的实际工程应用,为电子设备的电磁安全防护设计提供参考.
[1]刘培国, 刘晨曦, 谭剑锋, 等.强电磁防护技术研究进展[J].中国舰船研究, 2015, 10(2):2-6.
LIU P G, LIU C X, TAN J F, et al.Analysis of the research development on HPM/EMP protection[J].Chinese journal of ship research, 2015, 10(2):2-6.(in Chinese)
[2]HOCKANSON D M, YE X N, DREWNIAK J L, et al.FDTD and experimental investigation of EMI from stacked-card PCB configurations[J].IEEE transactions on electromagnetic compatibility, 2001, 43(1):1-9.
[3]CARPES W P, PICHON L Jr, RAZEK A.Analysis of the coupling of an incident wave with a wire inside a cavity using an FEM in frequency and time domains[J].IEEE transactions on electromagnetic compatibility, 2002, 44(3):470-475.
[4]BOGDANOV F G, KARKASHADZE D, JOBAVA R G, et al.Validation of hybrid MoM scheme with included equivalent glass antenna model for handling automotive electromagnetic compatibility problems[J].IEEE transactions on electromagnetic compatibility, 2010, 52(1):164-172.
[5]阚勇, 闫丽萍, 赵翔, 等.基于电磁拓扑的多腔体屏蔽效能快速算法[J].物理学报, 2016, 65(1):030702.
KAN Y, YAN L P, ZHAO X, et a1.Electromagnetic topology based fast algorithm for shielding effectiveness estimation of multiple enclosures with apertures [J].Acta physica sinica, 2016, 65(1):030702.(in Chinese)
[6]王利萍, 周东方, 彭强, 等.基于拓扑网络的屏蔽腔体内置微带线响应分析[J].电波科学学报, 2014, 29(1):321-327.
WANG L P, ZHOU D F, PENG Q, et a1.Response analysis of microstrip lines in the shielding cavity based on topological network[J].Chinese journal of radio science, 2014, 29(1):321-327.(in Chinese)
[7]YU Q, WANG Y D, HAN J H.The terminal responses of lossy microstrip line illuminated by a plane wave[C]//2011 IEEE International Conference on Microwave Technology &Computational Electromagnetics, 2011, 5:897-900.
[8]张悦, 刘尚合, 胡小锋, 等.不同辐射源瞬态电磁信号辐射场特性研究[J].电波科学学报, 2015, 30(2):316-322.
ZHANG Y, LIU S H, HU X F, et a1.Properties of transient electromagnetic signals radiation field from various radiation sources[J].Chinese journal of radio science, 2015, 30(2):316-322.(in Chinese).
[9]ZHENG X.Statistics of impedance and scattering matrices in chaotic microwave cavities:the random coupling model[D].University of Maryland, 2005.
[10]HEMMADY S D.A wave-chaotic approach to predicting and measuring electromagnetic field quantifies in complicated enclosures[D].University of Maryland, 2006.
[11]刘尚合, 刘卫东.电磁兼容与电磁防护相关研究进展[J].高电压技术, 2014, 40(6):1605-1613
LIU S H, LIU W D.Progress of relevant research on electromagnetic compatibility and electromagnetic protection[J].High voltage engineering, 2014, 40(6):1605-1613.(in Chinese)
[12]闫二艳.波混沌腔体中电磁效应物理量的统计特性研究[D].绵阳:中国工程物理研究院, 2009.
YAN E Y.The statistic characteristic research of electromagnetic effect physical quantity in chaotic cavity[D].Mianyang:China Academy of Engineering Physics, 2009.(in Chinese)
[13]闫二艳, 孟凡宝, 马弘舸.微波混沌腔体中的散射特性研究[J].物理学报, 2010, 59(3):1568-1675.
YAN E Y, MENG F B, MA H G.Research on scattering in microwave chaotic cavity[J].Acta physica sinica, 2010, 59(3):1568-1675.(in Chinese)
[14]庄信武, 余志勇, 刘光斌, 等.混沌腔体的统计电磁预测技术[J].强激光与电子束, 2014, 26(3):197-203.
ZHUANG X W, YU Z Y, LIU G B, et a1.Electromagnetic statistical prediction of chaotic cavities[J].High power laser and particle beams, 2014, 26(3):197-203.(in Chinese)
[15]庄信武, 余志勇, 刘光斌, 等.复杂腔体电磁混沌特性统计分析[J].电波科学学报, 2015, 30(3):597-602.
ZHUANG X W, YU Z Y, LIU G B, et a1.Statistical analysis on EM chaos characteristics for complex cavity[J].Chinese journal of radio science, 2015, 30(3):597-602.(in Chinese)
[16]陆希成, 王建国, 刘钰.基于天线辐射理论构建微波混沌腔的随机耦合模型[J].物理学报, 2013, 62(7):070504.
LU X C, WANG J G, LIU Y.Based on antenna theory to establish the random coupling model of microwave chaotic cavities[J].Acta physica sinica, 2013, 62(7):070504.(in Chinese)
[17]郝建红, 孙娜燕, 高璞, 等.场路结合法分析设备电磁辐照效应[J].电波科学学报, 2012, 27(2):359-364.
HAO J H, SUN N Y, GAO P, et a1.Analysis of the electromagnetic radiation effect of the equipment by field-circuit method[J].Chinese journal of radio science, 2012, 27(2):359-364.(in Chinese)
[18]范杰清.复杂金属腔体高功率微波耦合效应研究[D].北京:华北电力大学, 2015.
FAN J Q.Study on effect of HPM coupling on complex metal cabity[D].Beijing:North China Electric Power University, 2015.(in Chinese)
[19]宋子贤.基于RCM的混沌腔体耦合特性的研究[D].北京:华北电力大学, 2015.
SONG Z X.Analysis of electromagnetic coupling properties for chaotic cavity based on RCM[D].Beijing:North China Electric Power University, 2015.(in Chinese)
[20]HART J A, ANTONSEN T M, OTT E.Effect of short ray trajectories on the scattering statistics of wave chaotic systems[J].Physical review E, 2009, 80:041109.
[21]YEH J H, HART J A, BRADSHAW E, et a1.Experimental examination of the effect of short ray trajectories in two-port wave-chaotic scattering systems[J].Physical review E, 2010, 82:041114.
[22]YEH J H, HART J A, BRADSHAW E, et al.Universal and nonuniversal properties of wave-chaotic scattering systems[J].Physical review E, 2010, 81:025201.
[23]YEH J H.Wave chaotic experiments and models for complicated wave scattering systems[D].University of Maryland, 2013.

李福林 (1979-),男,河北人,解放军信息工程大学博士研究生,副教授,主要研究方向为电子设备电磁脉冲效应分析.

韩继红 (1966-),女,山西人,解放军信息工程大学教授,博士生导师,博士,主要研究方向为电子设备电磁脉冲效应分析及安全防护、安全协议分析与验证.

张畅 (1981-),男,湖北人,解放军信息工程大学博士研究生,讲师,主要研究方向为电子设备电磁安全防护.
Short-orbit random coupling model in two-port wave-chaotic cavity
LI Fulin1,2HAN Jihong1,2ZHANG Chang1
(1.PLAInformationEngineeringUniversity,Zhengzhou450001,China;2.PLAKeyLaboratoryofInformationSecurity,Zhengzhou450001,China)
The traditional random coupling model sets boundary conditions at infinity in calculating the effect of electromagnetic pulse with the electronic equipment, which causes a problem named short-orbit effects.In order to decrease the effect existed in the traditional random coupling model, a short-orbit random coupling model (SORCM) of the two-port wave chaotic cavity is proposed by defining a short-orbit correction coefficient of the radiation impedance.The variation of root-mean-square error of induced voltage at the target point is analyzed with the largest short-orbit length.In different frequency range, the statistical characteristics and calculated results of the SORCM are compared with experimental data which can verify the correctness of the model.Theoretical analysis and experimental results show that the SORCM is more effective compared with the traditional random coupling model.It can be used to predict and analyze electromagnetic pulse effects of the complex electronic equipment.
wave-chaotic cavity;electromagnetic pulse effect;short-orbit random coupling model;radiation impedance
李福林, 韩继红, 张畅.二端口波混沌腔体短迹线随机耦合模型[J].电波科学学报,2016,31(5):912-919.
10.13443/j.cjors.2016070501
LI F L, HAN J H, ZHANG C.Short-orbit random coupling model in two-port wave-chaotic cavity[J].Chinese journal of radio science,2016,31(5):912-919.(in Chinese).DOI:10.13443/j.cjors.2016070501
2016-07-05
国防科研项目
O414.2;O415.5
A
1005-0388(2016)05-0912-08
联系人:李福林 E-mail:leefulin@163.com

