扫描波束天线无相位近场测量技术

尚军平 左炎春 胡永浩 王媛 宋康

(西安电子科技大学 天线与微波技术国防科技重点实验室,西安 710071)



扫描波束天线无相位近场测量技术

尚军平 左炎春 胡永浩 王媛 宋康

(西安电子科技大学 天线与微波技术国防科技重点实验室,西安 710071)

以寻找高频扫描波束天线近场测量方法为目的,提出了一种结合差分进化算法和迭代傅里叶变换算法的双平面无相位近场测量方法.首先用线极化探头在近区采集正交方向切向场幅值信息;其次使用差分进化算法寻找合适的初始迭代相位;再利用迭代傅里叶变换算法对一扫描面上的相位进行还原;最后使用采样幅值和还原相位结合近远场变换理论求得天线远场方向图.为验证方法可行性,以对称振子天线阵为模型,对不同扫描角时的测量过程进行仿真,均获得良好结果.

无相位测量;扫描波束天线;近场测量;差分进化算法;迭代傅里叶变换算法

DOI 10.13443/j.cjors.2016042501

引 言

在导航、雷达、通信等系统中,高增益、低副瓣、波束指向可调的扫描波束天线备受青睐,其设计和调试往往需要多次测量.传统的天线近场测量方法是[1],获取天线近区一扫描平面上的切向场幅值和相位信息,借助近远场变换理论求得天线的远场方向图.但随着天线工作频率的提升,由于探头定位误差、测量成本等因素的制约,近场相位获取越发困难,致使高频段天线测量成为一大难题.Tim H.Taminiau等人使用单荧光分子探头实现了光波段天线测量[2],但该方案需要苛刻的实验条件,很难在现有天线暗室实施.

针对高频天线测量问题,Samii团队提出了双极平面无相位近场测量技术[3],其在天线近场区设置两扫描平面,使用双极平面采样技术获取扫描点位置的切向场幅值信息,并利用迭代傅里叶变换算法(Iterative Fourier Transform Algorithm,IFTA)对扫描点位置场相位进行还原.由于仅进行幅值采样和使用算法还原相位,使得测量成本大大降低，方向图重建精度提高.但IFTA是局部优化算法,常因陷入局部最优解而无法对扫描波束天线近场相位进行准确还原,因此,需找一种适合扫描波束天线的无相位近场测量方法.

H.Shakhtour等人使用无相位近场测量技术实现天线罩特性的测量[4],Gary Junkin等人则用并行计算技术对多种相位还原算法加速问题进行讨论[5]等等,这些成果说明,作为前瞻性研究,国际上对无相测量技术的研究无论是理论上还是在应用上正趋向成熟.

本文则是在Samii双极平面无相位测量技术的基础上,将差分进化算法(Differential Evolution Algorithm,DEA)[6-7]引入到初始迭代相位寻找中,对初始迭代相位进行优化,研究了一种近场矩形栅格无相位扫描波束天线测量方法.并以阵列天线为模型,仿真多组不同扫描角情况下的测量过程,验证了测量方法的收敛精度和速度.

1 基于IFTA的矩形栅格近场无相位测量基本原理

基于IFTA的无相位近场天线测量的基本思想是,在天线近区两平行平面上采集天线产生切向场的幅值信息,使用IFTA技术对一扫描面上各扫描点位置的相位进行还原,并借助近远场变换理论求得天线的远场方向图.测量模型如图1所示,待测天线口径面位于xoy面上,并在z=d1和z=d2处设置两扫描平面,命名为#1和#2平面,按照.Nyq-uist采样定理采集两平面的切向场幅值信息,记为|M#1|和|M#2|.

图1 无相位近场天线测量系统原理模型图

1.1 基于IFTA的采样点相位还原

相位还原算法需要一个初始迭代相位.波束指向在口径法向的天线近场无相测量中,初始相位的产生主要有两种方式:第一,随机初始迭代相位(下称初始条件1),即给每一个扫描点赋以随机相位;第二,基于口径形状的初始相位(下称初始条件2),即将天线口径面或者等效口径面进行矩形网格划分,在天线口径区内网格结点上安放无限小偶极子,并令其激励电流为1,口径面外不设置偶极子,使用场叠加定理确定采样点位置的相位作为初始相位.

在给定初始相位前提下,扫描点位置的相位还原步骤是:第一步,调用已经采集的双平面幅值信息;第二步,在初始条件1(或初始条件2)下结合采样幅值给定#1平面采样点位置的复数场;第三步,使用平面波谱理论由#1平面场分布求得#2平面场分布,并使用测量幅值替代计算幅值;第四步,依然使用平面波谱理论和#2平面替代场求得#1平面场分布,并使用离散均方误差来进行误差衡量.如果误差满足设定值,或者达到最大迭代次数,则迭代过程停止,否则,在#1平面上进行幅值替代,返回第三步继续进行,算法流程如图2所示.

图2 相位还原算法流程图

1.2 基于平面波谱理论的远场方向图计算方法

如图1所示,当待测天线口径面位于xoy平面上,在z=d1设置一个扫描平面,且使用#1平面上还原相位和采样幅值构成的场(以下简称还原场)分布为E(x,y,d1),则天线的远场方向图函数在球坐标系下可以表示为[1]

(1)

式中,

=ejkzd1·F[E(x,y,d1)],

(2)

F是二维傅里叶算符.同样若已知波谱A(kx,ky),可得E(x,y,d1),即

(3)

式中,k·r=k(sin θcos φ·x+sin θsin φ·y+cos φ·z).

进一步推导可知,天线近场区z=d1平面和z=d2平面切向场之间关系可以表示为

(4)

该式是1.1节中基于IFTA的相位还原技术的理论基础.

1.3 基于IFTA的扫描波束天线测量低鲁棒性说明

使用上述提及方法对扫描波束天线进行了测量,图3分别给出在初始条件1和初始条件2以及扫描角为θ=5°和θ=15°下进行的无相位测量E面计算结果.可以清楚地看到,两种初始迭代相位均不能使IFTA有效捕捉主波束方向,且收敛波束指向均为0°.这主要是因为,IFTA是局部优化算法,其对初始条件要求很高,不佳的初始条件将使算法陷入局部最优解,无法确定准确相位分布.

(a) θ=5°

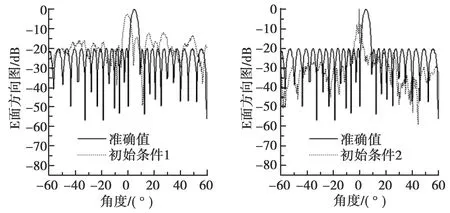
(b) θ=15°图3 两种初始条件下扫描波束天线E面比较图

2 扫描波束天线近场无相位测量基本原理

由上述分析可知,迭代初始相位对相位还原精度影响很大,因此,本文首先使用DEA优化初始迭代相位;再使用IFTA对扫描点位置的相位进行精细还原;最后,由一扫描面的幅度和还原相位通过近远场变换求得天线的远场方向图.

2.1 基于DEA的初始迭代相位计算

已经知道,波束指向为(θ0,φ0)的平面波可以表示为E=E0e-jk(sin θ0cos φ0x+sin θ0sin φ0y+cos φ0z),其中,E0表示平面波的振幅矢量,k是传播常数.如假设天线口径面场分布为

Eapature=MAUT(x,y)·

e-jk(sin θ0cos φ0x+sin θ0sin φ0y+cos φ0z).

(5)

由平面几何绕射理论可知,由口径场分布可唯一确定#1平面场分布,因此,每一组(θ,φ)均对应#1平面上的一种场分布可能.由于已进行幅值采样,因此,可使用DEA寻找使得测量幅值与计算幅值差异最小的组合(θbest,φbest),并命该组合对应的#1平面相位分布作为初始迭代相位,记为初始条件3,其有如下搜索步骤．

1) 目标函数、适应度函数选取

为了实测方便,本文将目标函数和适应度函数置成相同,并按照如下方法生成:

步骤1 使用式(4)、(5)可求得任意给定一组(θg,i,φg,i)条件下的#1平面场分布;

步骤2 同1.1节的第三步,使用测量幅值替代计算幅值,并使用平面波谱理论由#1平面替代场求得#2平面的场分布,同1.1节中第四步,使用测量幅值替代计算幅值,并再次使用平面波谱理论由#2平面替代场求得#1面的场分布E#1,g,i;

步骤3 使用离散均方误差来度量(θg,i,φg,i)的适应度,即第g代第i个个体的适应度为

f(g,i)=

(6)

式中,|E#1,g,i|是由上一步获得的E#1,g,i进一步计算得到的#1平面M×N阶切向场幅值矩阵.

2) 波束指向角的搜寻

有了目标函数和适应度函数,下面使用DEA寻找使适应度函数取得最小值的(θ,φ)组合,由于天线的波束指向前半区域,因此,优化角的选择为θ∈[-90°,90°],φ∈[-180°,180°],并记Φi(g)=(θi,φi)为算法中的第g代第i个个体.表1给出了DEA的参数设置.

表1 DEA参数设置表

在此基础上,有如下的搜寻步骤:

步骤1 随机产生初始种群:

(7)

步骤2 选择放缩因子F=0.5,进行变异操作:

(8)

对于变异越界的值使用下式值予以替代:

(9)

步骤3 设置交叉概率P=0.3进行交叉操作, jrand是等于1或2的随机整数,即

uj,i(g+1)

(10)

步骤4 选择操作.按照上文选择的适应度函数,其值越小表明所选择的(θ,φ)组合计算出来的场的误差越小,因而适应度越高,这样的个体是需要保留的,即

(11)

式中,函数f(g,i),fu(g+1,i)分别表示Φi(g)和ui(g+1)的适应度.经过多代进化,最终可选择出与天线波束指向较为接近的(θ,φ)组合.

3) 初始迭代相位的生成

通过上述过程可获取与真实波束指向误差较小的(θbest,φbest)组合,使用式(4)和(5)可以求得#1平面的相位分布为φ0,即

(12)

2.2 基于IFTA的扫描点位置相位还原及远场方向图计算

使用上述生成的初始迭代相位φ0,结合1.1节中的IFTA相位还原方案,可以有效还原#1平面的扫描点位置的相位.

由上述还原相位和#1平面的采样幅值构成#1平面还原场,依据上文提及的近远场变换理论求得天线的远场方向图.上述扫描波束天线无相位测量方案可绘制如图4所示的算法流程图.

图4 扫描波束天线无相位测量流程图

2.3 基于DEA-IFTA相位还原算法收敛性说明

首先,IFTA是交替投影算法的具体应用,由场的唯一性定理可知,在天线近场不同位置设置的两平行平面上的相位分布不同.因此,只需要寻找包含双平面准确相位的且交集为空的两个投影集合,并保证它们是凸集,就可以在数学上保证迭代过程收敛于两个集合的不动点[8],这个不动点就是双平面准确相位分布.

其次,DEA是全局优化算法,其收敛性已经被证明[8].换言之,基于DEA的初始迭代相位生成方案可生成包含准确相位且交集为空的两个投影集合.这是因为,DEA具有全局收敛特性,且只有准确的相位分布才能使式(6)定义的误差函数取得最小值.因此,DEA通过反复迭代可使初始迭代相位充分接近准确相位,上文已指出,双平面准确相位不同,因此,随着DEA迭代进程,总存在两个包含准确相位且交集为空的凸集满足IFTA的收敛条件.

DEA为IFTA提供优质的初始迭代条件(收敛条件),在此条件下IFTA可以得到满意的收敛效果,因此,基于DEA-IFTA相位还原算法可有效实现扫描面相位还原.

3 算法仿真

为验证上述测量理论,使用19×19半波对称振子阵列天线进行仿真,仿真天线位于xoy平面上,阵元在x和y方向的单元间距均为0.5λ,并分别采用余弦分布和切比雪夫分布电流给予激励,两采样平面距口径面4λ和4.3λ平行放置,采样点数均为401×401,采样间隔均为0.5λ.设置最大迭代次数为1 500次,误差限为ε0=50 dB.

首先,使用DEA对天线的波束指向进行确定.按照上文所述步骤,表2给出了准确波束指向角(θ,φ)为(5°,90°)、(10°,90°)、(15°,90°)三种情况下使用DEA得到的波束角与准确值的比较.图5(a)给出了初始条件3下,准确值θ=5°时实验迭代误差与迭代次数之间的关系.可以看出,使用差分进化算法可以有效寻找到波束指向角,并且较少的迭代次数就可以得到稳定解.

表2 波束指向角寻找结果

其次,将DEA得到的角度带入式(12)生成初始相位,并使用1.1节中的IFTA对#1平面扫描点位置的相位进行还原.迭代误差与迭代次数的关系如图5(b)所示．可以看出,当迭代次数较少时,误差曲线陡峭,但到达一定的迭代次数后,误差曲线变化趋于平缓,这是因为算法已经寻找到较为稳定的解.表3给出了迭代1 500次后,#1平面上由式(6)定义的离散均方误差.对比图5(a)与5(b)、表2与表3可知,经过IFTA的处理,#1扫描面上的均方误差有大幅度下降.图5(c)～(d)给出了使用DEA-IFTA处理后准确值为θ=5°情况下使用还原场计算得到的E面、H面方向图与理想方向图的比较,对比图3可以看到,主瓣和前几个副瓣的吻合度有明显提高,从而证明了上文阐述算法的合理性.

(a) DEA误差收敛曲线 (b) IFTA误差收敛曲线

(c) E面方向图 (d) H面方向图图5 θ=5°时扫描波束天线无相位测量结果图

波束指向角/(°)迭代次数最小均方误差/dB5.0001500-36.113910.0001500-28.973915.0001500-30.7403

最后,多组仿真数据还表明:阵列天线扫描角θ、φ在-60°～60°之间,且主波瓣宽度不小于10°时,本文所述的方法具有很好的精度.当扫描角大于或接近60°时,受截断误差影响,近场幅值数据获取精度恶化,致使上述相位还原算法收敛精度较差;同时,当主波瓣宽度小于10°时,将导致波束指向角捕捉困难,进而影响初始迭代相位精度,并最终影响远场方向图重建准确度.

4 结 论

本文针对高频扫描波束天线测量问题,提出了一种基于DEA和IFTA的无相位近场测量方案,首先使用DEA寻找合适的初始迭代相位,再使用IFTA对扫描点位置的相位进行精细还原,最后通过近远场变换求得天线的远场方向图.仿真实验表明,使用全局优化算法DEA和局部优化算法IFTA相结合的组合优化算法可以有效解决对扫描波束天线的波束指向进行有效捕捉这一问题.本文对扫描波束天线无相近场测量技术的研究处于仿真验证阶段,实际测试验证还有待进一步研究.

[1]YAGHJW A D.An overview of near-field antenna measurements[J].IEEE transactions on antennas and propagation, 1986, 34(1)：30-44.

[2]TAMINIAU T H, SEGERINK F B, VAN HULST N F, et al.A monopole antenna at optical frequencies：single-molecule near-field measurements[J].IEEE transactions on antennas and propagation, 2007, 55(11)：3010-3017.

[3]RAZAVI S F, RAHMAT-SAMII Y.Phaseless measurements over nonrectangular planar near-field systems without probe corotation[J].IEEE transactions on antennas and propagation, 2012, 61(1)：143-152.

[4]SHAKHTOUR H, BERLING D H.Phaseless planar near-field antenna measurements：some aspects of aperture's mask and alignment error[J].Electronics letters, 2015, 51(17)：1308-1310.

[5]JUNKIN G.Planar near-field phase retrieval using GPUs for accurate THz far-field prediction[J].IEEE transactions on antennas propagation, 2013, 61(4)：1783-1775.

[6]王安娜, 章文勋.用于天线优化的改进差分进化算法[J].电波科学学报, 2009, 24(5)：808-812.

WANG A N, ZHANG W X.Improved differential evolution for antenna optimization[J].Chinese journal of radio science, 2009, 24(5):808-812.(in Chinese)

[7]ELSAYED S M, SARKER R A, ESSAM D L.An improved self-adaptive differential evolution algorithm for optimization problems[J].IEEE transactions on antennas and propagation, 2013, 9 (1)：89-99.

[8]万雪杰.交替投影算法的应用[D].郑州:郑州大学,2009.

WAN X J.The application of alternating projection method[D].Zhengzhou：Zhengzhou University, 2009.(in Chinese)

[9]彭智, 谢玲.混合优化算法的全局收敛性分析[J].北京理工大学学报, 2012, 32(4)：435-440.

PENG Z, XIE L.Global convergence analysis of hybrid optimization algorithms[J].Transactions of Beijing Institute of Technology, 2012, 32(4)：435-440.(in Chinese)

尚军平 (1964-)，男，陕西人，西安电子科技大学副教授，硕士生导师，博士，研究方向为天线近远场测试技术及应用、无线网络通信技术等.

左炎春 (1989-)，男，河南人，西安电子科技大学在读硕士研究生，研究方向为无相位近场天线测量技术等.

胡永浩 (1991-)，男，河南人，西安电子科技大学在读硕士研究生，研究方向为极平面天线近场测量技术、天线设计等.

王媛 (1993-)，女，山西人，西安电子科技大学在读硕士研究生，研究方向为无相位近场天线测量技术.

宋康 (1993-)，男，山东人，西安电子科技大学在读硕士研究生，研究方向为天线中场测量技术等.

Phaseless near-field measurement of scanned bean antenna

SHANG Junping ZUO Yanchun HU Yonghao WANG Yuan SONG Kang

(NationalKeyLaboratoryofAntennaandmicrowave,XidianUniversity,Xi’an710071,China)

For finding the method to measure the high frequency scanned bean antenna, this paper presents a method combing differential evolution algorithm with iterate Fourier transform algorithm to determine the far-field pattern of the antenna under test.This method firstly collects the field amplitudes in two orthogonal directions on two scanning planes in the near-field region of the antenna with linear polarization probe.Secondly, an appropriate initial iterate phase distribution is obtained by applying the differential evolution algorithm to the collected field amplitude data.Thirdly, iterate Fourier transform is chosen to revival the phase distribution on one of the scanning planes.Finally, far-field pattern can be reconstructed according to the near-field far-field transform theory.A simulation is performed in different bean direction angles which confirm the good performance of the presented method.

phaseless measurement;scanned bean antenna;near-field measurement;differential evolution algorithm;iterative Fourier transform algorithm

尚军平, 左炎春, 胡永浩, 等.扫描波束天线无相位近场测量技术[J].电波科学学报,2016,31(5):864-869.

10.13443/j.cjors.2016042501

SHANG J P, ZUO Y C, HU Y H, et al.Phaseless near-field measurement of scanned bean antenna[J].Chinese journal of radio science,2016,31(5):864-869.(in Chinese).DOI：10.13443/j.cjors.2016042501

2016-04-25

TM937.2

A

1005-0388(2016)05-0864-06

联系人：尚军平 E-mail：jpshang@mail.xidian.edu.cn