基于支持向量机的粗糙海面风速及海表盐度反演研究

张清河 梁伟博

(三峡大学理学院,宜昌 443002)



基于支持向量机的粗糙海面风速及海表盐度反演研究

张清河 梁伟博

(三峡大学理学院,宜昌 443002)

将支持向量机(Support Vector Machine,SVM)回归技术应用到海况参数(如海表盐度、海面风速等)反演研究.利用双尺度模型(Two-Scale Model,TSM)作为前向电磁算法,数值模拟不同雷达参数下风驱粗糙海面微波后向散射系数,经过敏感性分析,选取L波段(1.4 GHz)、C波段(6.8 GHz)及其合适的入射角作为雷达参数,并设计多种反演方案,分别以单频率双极化双角度、双频率双极化双角度及双极化后向散射系数的比值作为SVM的训练样本数据信息,经过适当的训练,利用SVM回归技术对海洋表面风速和盐度进行了反演研究.研究结果表明,针对于海面风速的反演,C波段的反演精度最高,针对于海表盐度的反演,L波段同极化散射系数比值作为SVM输入的反演精度较高.最后,检验了SVM反演方法的抗噪声性能,表明文中提出的SVM方法能较好地应用于实际海况参数反演问题.

支持向量机;双尺度模型;反演;海面风速;海表盐度

DOI 10.13443/j.cjors.2015102601

引 言

海面风速是研究海气之间相互作用的重要参数,它对短期预报以及季节性和气候年际变化的预测非常重要,海面风速通过调节热量、水汽、海气通量和颗粒物,调节大气和海洋之间的耦合作用,从而维持全球和区域气候[1].海表面盐度 (Sea Surface Salinity,SSS)是海洋的一个重要物理化学参量,观测海洋盐度可以帮助我们加强对全球水循环的理解.同时,海洋盐度在碳循环中也起到了重要作用,为估计海洋CO2的吸收释放量提供了可靠依据[2].由于海面上空复杂天气条件的限制,以及可见光-近红外波谱穿透云雾能力的局限性,微波遥感所具有的全天时、全天候工作能力并对某次海洋参数和状态(盐度、温度、风速等)具有独特的大面积、快速、定量检测能力而受到人们的关注.因此,海洋盐度和风速反演成为海洋微波遥感的重要目标.

近二十年来,已有许多学者利用星载微波数据进行了海面风速和海表盐度的反演研究.在海面风速反演方面,目前利用星载微波散射计反演海面风速大致可以分为两类.一是利用地球物理模型函数的反演方法[3-9],地球物理模型函数是指海面雷达后向散射系数或归一化雷达后向散射截面与海面风速、风向、雷达观测参数以及海面环境参数等之间的定量函数关系,由于电磁波与海表面相互作用的复杂性,因此这种关系大多是通过统计方法来建立经验模型函数,目前使用较多的有C波段的CMOD系列模型函数和Ku波段的NSCAT系列模型函数.虽然利用地球物理模型函数的反演方法经过多年来的研究已日趋成熟,但由于该方法的数学复杂性、数值计算量大、优化参数过多,特别是模糊去除问题,仍然面临进一步的研究和完善.第二类是基于全球导航卫星系统反射信号(Global Navigation Satellite System Reflection,GNSS-R)的反演方法[10-11],该技术以L波段的导航卫星为信号源,通过GNSS直射信号和海面反射信号的同步接受,采用双基雷达前向散射模式进行海面风速的探测.第三类是基于神经网络、遗传算法等人工智能技术的反演方法[12-14].这类方法不依赖于具体模型函数,通过直接将雷达后向散射系数与海面风场建立联系来反演风速,为海面风速反演研究提供了一种新途径,但由于该技术中固有的过学习、易陷入局部最优解等问题,影响了该方法在风速反演中的进一步研究.另外也有研究者利用高频地波雷达对海面状态进行监测,文献[15]利用OS081H高频地波雷达,采用最小二乘多波束法,对海面风速及风向进行了反演,有效地消除了风向模糊问题.在海表盐度反演方面,Gabarro 等[16]首次使用 L 波段微波辐射计对地中海西部海域进行长时期遥感观测, 并基于实测数据得出盐度反演经验模式.Ammar 等[17]使用神经网络方法反演粗糙海面盐度的精度达到 0.6 pus, 为盐度遥感反演提供了新途径.卢红丽等[18]利用土壤湿度与海水盐度(Soil Moisture and Ocean Salinity, SMOS)卫星数据,结合辐射传输模型,采用最小二乘法对海洋盐度进行了迭代反演,且反演精度达到了0.35 pus.由于单波段微波辐射计遥感盐度的精度受温度、风速、波高和氧气吸收等海洋大气参量的影响, 因此多波段、多极化数据融合成为提高盐度反演精度的有效途径[19].本文将同时利用多角度、多波段、多极化等信息来反演盐度,期望能获得较高的反演精度.

支持向量机[20](Support Vector Machine, SVM)是近年来在统计学习理论的基础上发展起来的一种新的通用学习方法.它有效解决了小样本、过学习、非线性、高维数据等问题,具有良好的推广性和较好的预测精确性[21].近年来,支持向量机被广泛应用于各类实际问题,例如图像检索[22]、文本分类[23]、广义预测控制[24]等.但在微波遥感海洋及海况参数方面,国内外还未见有相关文献报道.

本文利用支持向量机方法对海面风速及海表盐度反演问题进行研究.以双尺度模型(Two-Scale Model,TSM)作为风驱粗糙海面电磁模型,根据Windsat和SMOS遥感卫星参数,我们选取微波频率为6.8 GHz(C波段)和1.4 GHz(L波段).首先利用TSM数值模拟出不同入射角下的后向散射系数,经过敏感性分析,确定合适的雷达入射角.针对风速和盐度设计多种反演方案,以后向散射系数作为输入,相应的风速和盐度作为输出,对SVM进行训练,建立反演模型,对盐度和风速进行了实时反演.同时,根据TSM中同极化后向散射系数的比值与风速无关的特性,选择该比值作为反演数据,有效降低了粗糙海面对微波信号的影响,提高了盐度的反演精度.

1 风驱海面双尺度模型

双尺度模型是在基尔霍夫近似(Kirchhoff Approximation,KA)和小扰动模型(Small Perturbation Model,SPM)的基础上发展起来的, 海面可以看作由小尺度毛细波叠加在大尺度重力波上构成的一种复合粗糙表面.双尺度模型的大尺度长波分量和小尺度毛细波分量正好对应着海面对高频电磁波的两种后向散射机理:近垂直入射时的镜面反射和斜入射时的布拉格散射如图1所示.该方法在入射角为0°～70°时有较高的准确性.

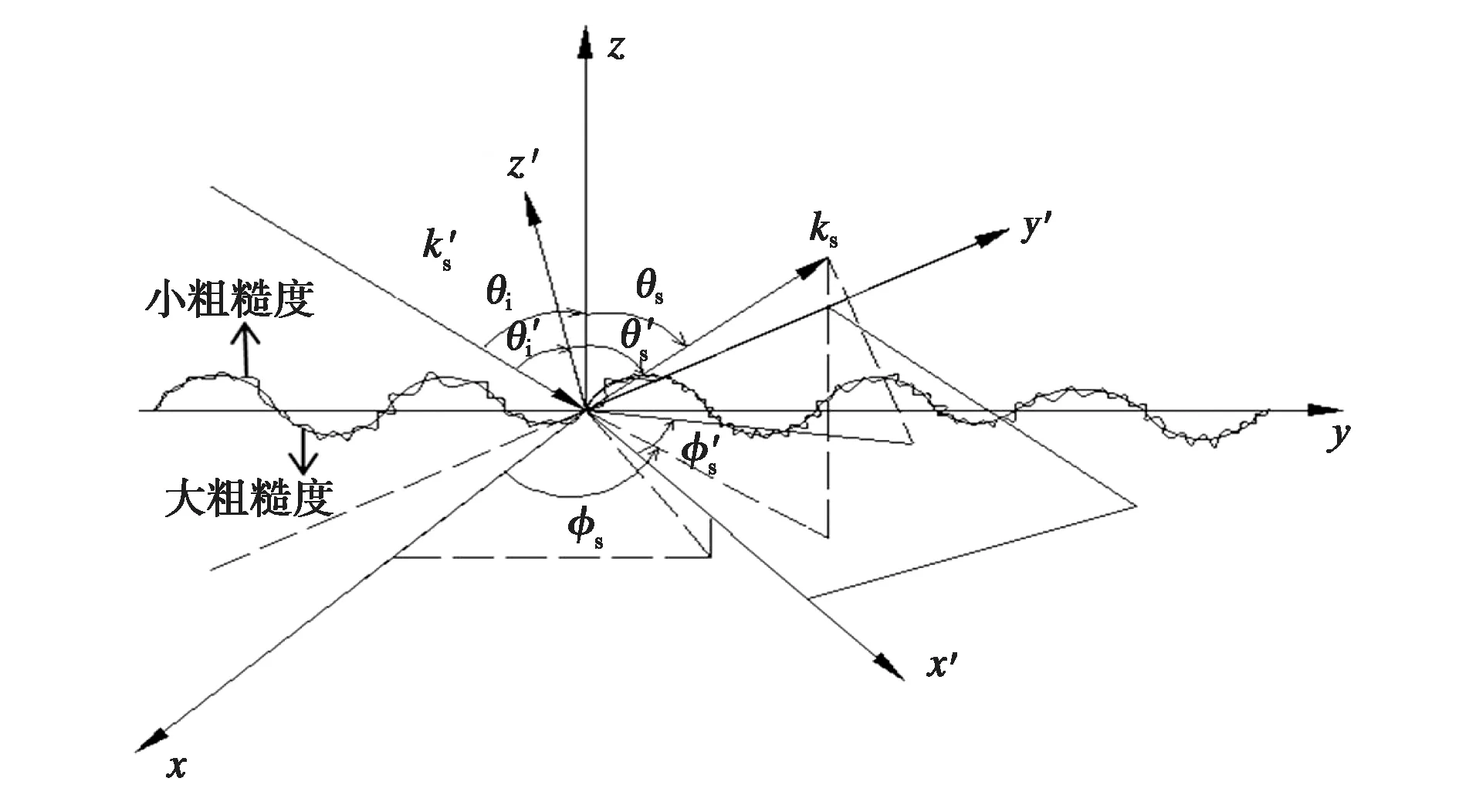
图1 双尺度粗糙海面的电磁散射示意图

假设大尺度波浪与小尺度波浪统计独立,用截断波数将海谱分割为两部分,然后采用KA和SPM分别计算两个尺度下的散射场,并对其求和得到粗糙海面总后向散射系数为[25-26]

σ=σS+σB.

(1)

一般认为,在逆风与侧风方向,大波浪斜率的二维概率分布函数服从高斯分布,其KA部分的后向散射系数可以表示为

(2)

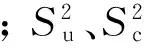
设入射面位于x-z平面中,则当入射波分别为水平极化和垂直极化时,SPM部分后向散射系数的计算公式为:

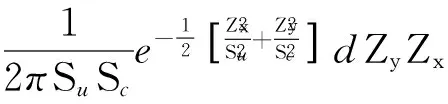
(3)

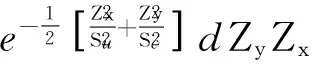
(4)

式中：Zx、Zy是局部坐标下大波浪斜率;θ′是局部坐标下的入射角,局部坐标系下的布拉格散射系数计算方法如下:

(5)

(6)

式中:

(7)

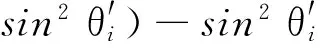
(8)

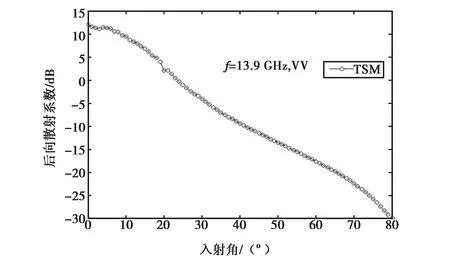
图2 VV极化后向散射系数随入射角的变化曲线

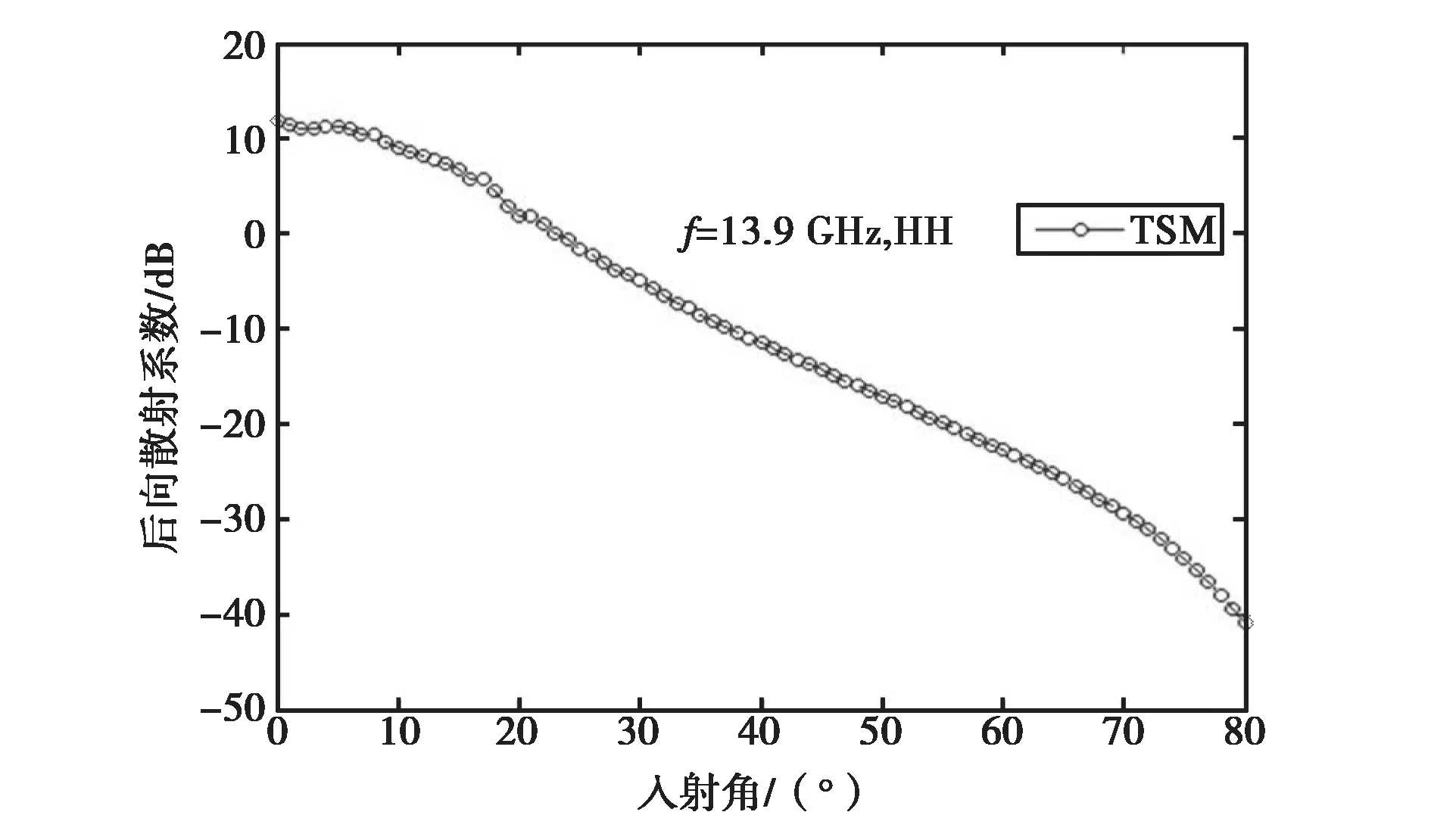
图3 HH极化后向散射系数随入射角的变化曲线

图2、3分别是采用与文献[25]相同海况参数及雷达入射频率(f=13.9 GHz)下,经TSM数值模拟的VV、HH极化后向散射系数与入射角的关系曲线.其中,粗糙海面采用DV海谱模型[25],在TSM模型中输入海况参数是海水介电常数,它与盐度的变换关系采用文献[27]中的双Debye海水介电模型.比较图2、3与文献[25]的结果,两者吻合得很好.后文中的海谱及海水介电模型均与本例相同.

2 敏感性分析

根据上述粗糙海面散射模型,海面风速及海表面盐度的变化会引起海面后向散射系数的变化,这是微波遥感测量海况参数的物理基础.同时,在海况参数一定的条件下,粗糙海面后向散射特性也与雷达参数有关.微波后向散射系数可表示成如下函数形式:

σ0=f(S,U,R).

式中：S代表海表面盐度;U代表海表面风速;R代表雷达参数(如频率、入射角及极化等).

当对海况参数进行反演研究时,重点就要对雷达参数进行敏感性分析.在本文研究中,为结合实际,雷达频率选取星载全极化微波辐射计Windsat 和SMOS传感器的工作频率,即C波段(6.8 GHz)和L波段(1.4 GHz).在Windsat中其平均地球入射角为53.8°,而SMOS传感器L波段入射角的变化范围较大,同时,在本文研究中为提高反演精度,对每一波段均采用双极化.所以当对雷达参数进行敏感性分析时,就必须对L波段入射角进行敏感性分析,期望找到合适的入射角,使得其后向散射系数对风速有较高的敏感性.图4是采用DV海谱,海面风速为10 m/s,温度为10 ℃,盐度为10‰时,在不同入射角情况下,利用TSM模拟的粗糙海面后向散射系数与风速的关系曲线.

从图4(a)、(b)来看,对于不同的极化方式,σ～u曲线基本上保持了相同的变化趋势,当入射角大于30°时,曲线对风速比较敏感,入射角较小时,曲线对风速不敏感,基本上保持不变.当入射角大于或等于40°时,VV极化与HH极化对应的散射系数均增加了40 dB左右,可以看出σ～u曲线对于大于或等于40°的入射角较敏感.为了使后向散射系数对风速保持较高的敏感性,原则上应该选取较高的雷达入射角,但是考虑到当入射角θ≥70°时,散射模型准确度不高,且后向散射较弱.同时,为了充分利用多入射角的后向散射信息,提高反演精度,本文选取双入射角共同进行反演.所以在对风速进行L波段的反演时,选取入射角为40°和50°.

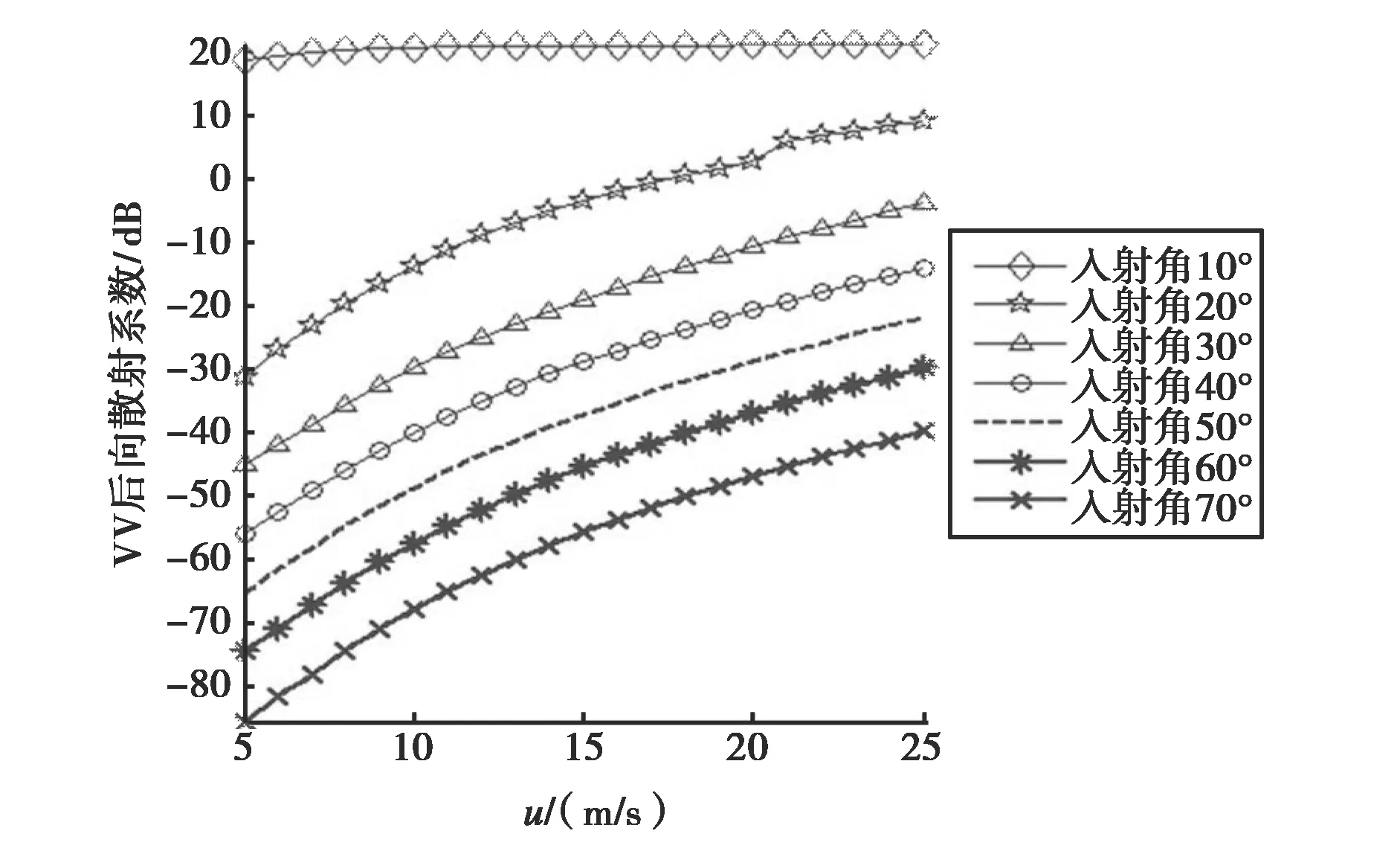
(a) VV极化

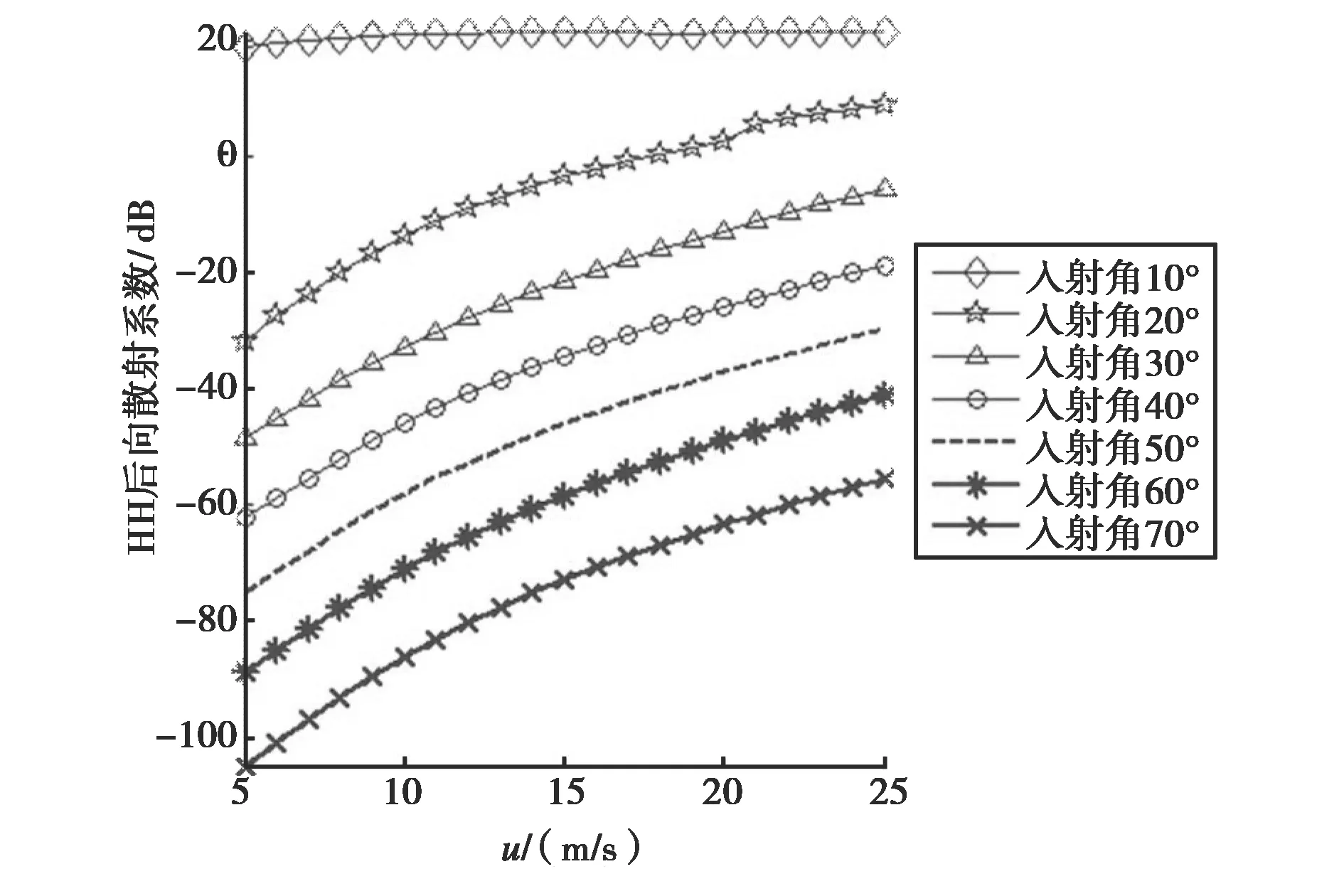
(b) HH极化图4 L波段、不同入射角下同极化后向散射系数与风速的关系曲线

当对海水盐度进行反演时,由于海面风速和海水盐度的变化都会引起后向散射系数的变化,因此,如何从微波信号中剔除海面风速对后向散射系数的影响一直是海表盐度反演中的关键问题.从公式(3)、(4)并结合式(7)、(8),当将式(3)、(4)相除,可消去粗糙海面功率谱函数W,取由式(7)、(8)计算的同极化后向散射系数比值时,可显著降低风驱粗糙海面对微波信号的影响.故在本文研究中,通过两个同极化后向散射系数相除,期望削弱风速对海面盐度反演的影响,提高反演精度.表1为在图2海况参数下,取入射角为40°和50°,雷达频率为1.4 GHz(L波段),基于TSM的同极化后向散射系数及其比值与风速的关系曲线的平均变化率.

由表1可以看出,VV极化和HH极化的后向散射系数关于风速的变化率都大于1,且是同极化比值变化率的500多倍,这说明同极化后向散射系数比值与风速的相关度较低,有效削弱了风速对海表盐度反演的影响.

图5是入射波频率为1.4 GHz,海面风速为10 m/s, 海表温度为10 ℃时,两个同极化后向散射系数比值在不同入射角下的变化率与海表盐度的关系曲线.

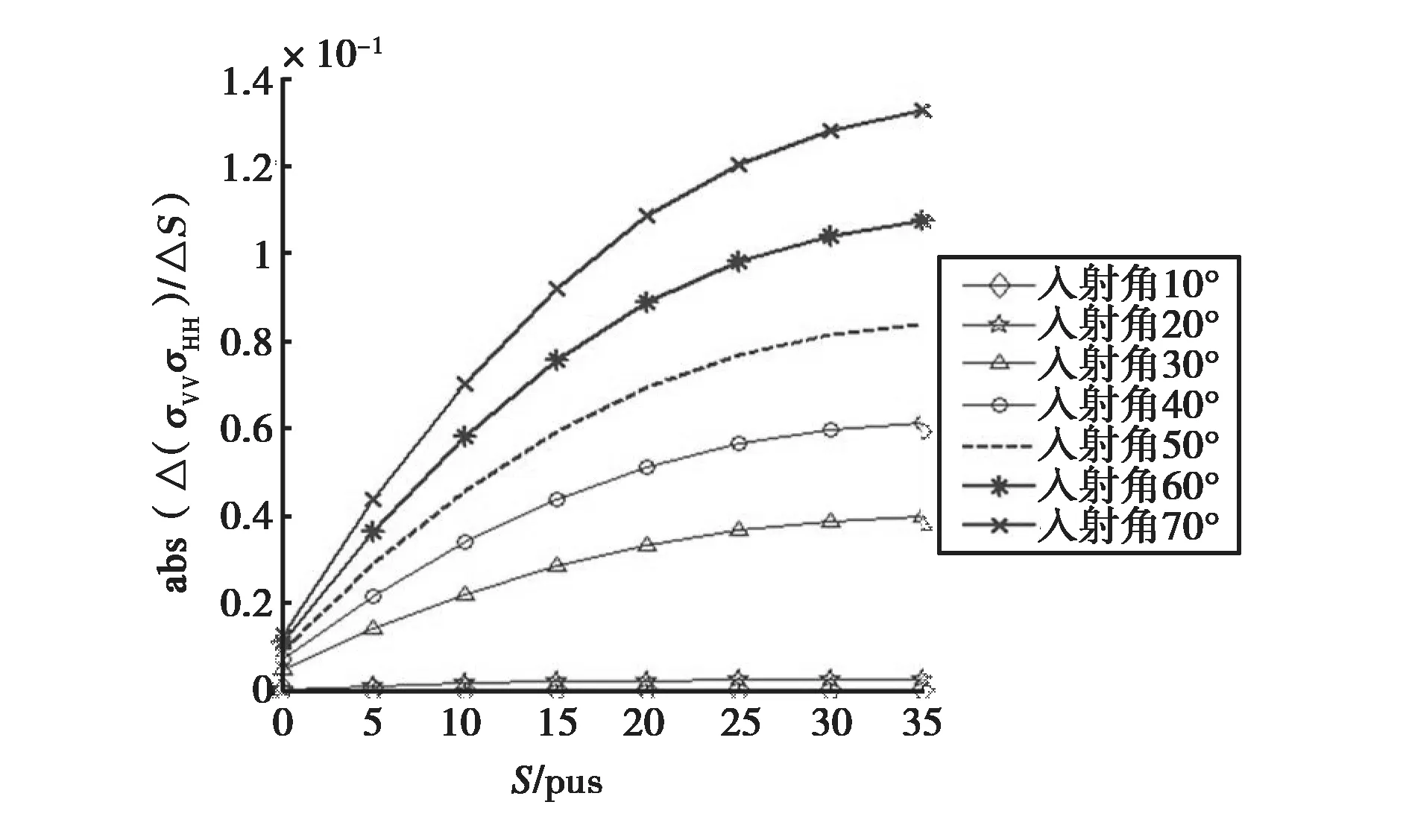
图5 L波段后向散射系数比值的变化率与盐度S的关系曲线

从图5可看出,当入射角增加时,散射系数比值的变化率增加,即当入射角越大时,同极化散射系数比值对于盐度越敏感.当入射角大于或等于40°时,散射系数比值的变化率均增加了5倍以上,可以看出比值对于盐度在入射角大于或等于40°时非常敏感.故在L波段下对盐度进行反演时,原则上应该选取较大的雷达入射角,但是考虑到前文中的前向散射模型准确度,并拟采用多入射角下的微波信号,本文在L波段下对盐度进行反演时,采用与反演风速时相同的雷达入射角.

3 反演方案设计

在基于SVM的海况参数反演问题中,首先利用双尺度模型生成数据样本,将样本按比例随机分成训练样本和测试样本,然后将训练样本的信息代入SVM模型中进行训练,得到相应反演模型,并利用测试样本检测反演模型的准确性.在TSM模型中,输入参数包括传感器雷达参数(频率、入射角、极化方式等)和海况参数(风速、盐度等).根据前文的敏感性分析,本文设计了三种反演方案,即首先针对L波段和C波段分别进行反演,然后再将L波段和C波段结合共同反演.其中L波段雷达入射角取为40°、50°,C波段雷达入射角取为53.8°.针对风速的反演,均采用双极化后向散射系数作为SVM的输入样本信息.当对盐度进行反演时,首先采用双极化后向散射系数组合进行反演,然后,考虑将两个同极化后向散射系数的比值作为SVM的样本信息,期望削弱风速对海面盐度反演的影响,提高反演精度.需要说明的是,在实际微波遥感海洋参数时,微波传感器接收到的是粗糙海面同极化后向散射系数,故本文先用TSM数值计算粗糙海面同极化后向散射系数σVV和σHH,再得到其比值,并以此作为SVM的输入信息来实现海表盐度的反演.表2是本文研究中海表参数的变化范围.这些参数的取值范围不仅在TSM模型的有效范围内,而且大多数粗糙海表的参数在其范围内.经TSM数值模拟,得到1 000个样本,其中训练样本比例为70%,测试样本比例为30%.

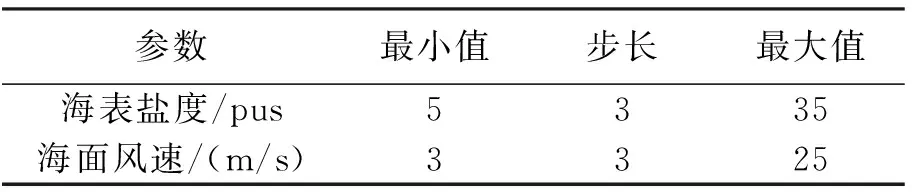
表2 双尺度数值模拟输入海况参数变化范围

4 数值结果与分析

4.1 风速反演结果与分析

将样本分为训练样本和测试样本,其中训练样本700个用于SVM训练学习,建立风速反演模型.剩余的300个测试样本用来检验该方法反演风速的精度.

首先,研究单频、双入射角、双极化情况下的风速反演,C波段的入射角为53.8°,L波段的入射角为40°、50°,海表温度设为15 ℃.图6(a)、(b)分别给出了L波段与C波段的反演值与真实值的对比结果.

从图6来看,两种波段下对风速的反演精度都较高.其中L波段的相关系数和均方根误差(Root Mean Squared Error,RMSE)为0.999 88和0.108 87,C波段的为0.999 94和0.071 867.L波段与C波段的相关系数差别不大,但是L波段的RMSE比C波段的RMSE大51%, 说明C波段反演风速的精度略高于L波段.

其次,将L波段与C波段的后向散射系数同时作为支持向量机的输入,同时考虑双入射角与双极化对风速进行反演,结果如图7所示.

(a) L波段

(b) C波段图6 单频、双入射角、双极化情况下的风速反演结果

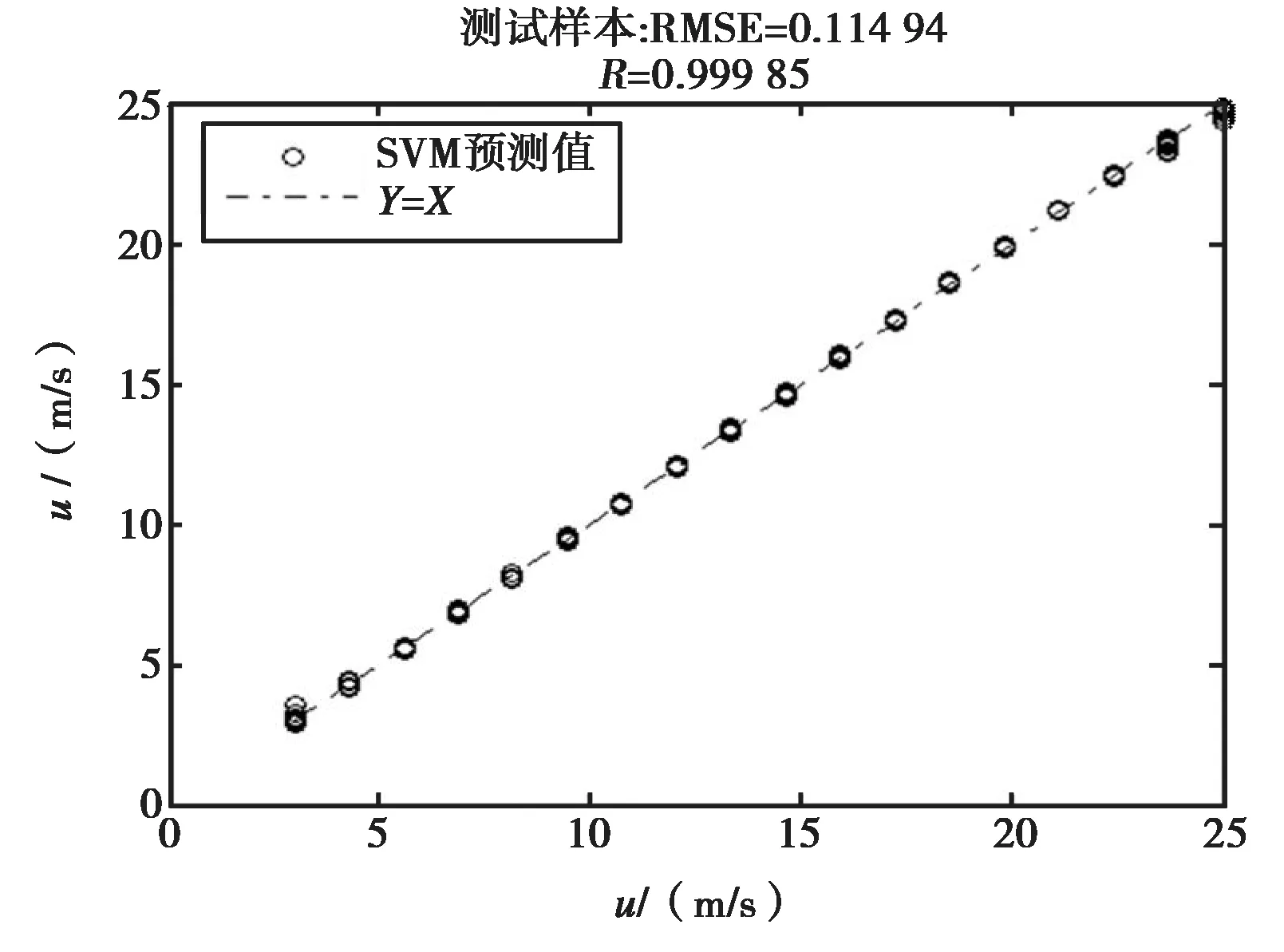
图7 双频率情况下的风速反演结果

从图7可以看出双波段下风速反演的相关系数为0.999 85,均方根误差0.114 94,与L波段的反演结果相当,略低于C波段下的反演精度.这说明在数据信息已较丰富的情况下(双入射角、双极化),单纯增加雷达频率并不能显著提高SVM的反演精度.

在实际应用中,传感器所接收的数据不可能就是数值模拟的数据,还可能包含各种各样的噪声和误差.为了讨论SVM反演方法的抗噪声性能,模拟实际应用中的电磁环境,对上例中的样本数据(后向散射系数)加上高斯随机噪声(设高斯随机噪声的标准差为D),再以此作为SVM的输入.图8(a)、(b)、(c)分别是取D=0.3, 0.6, 0.9时,加噪后的海面风速的反演结果.

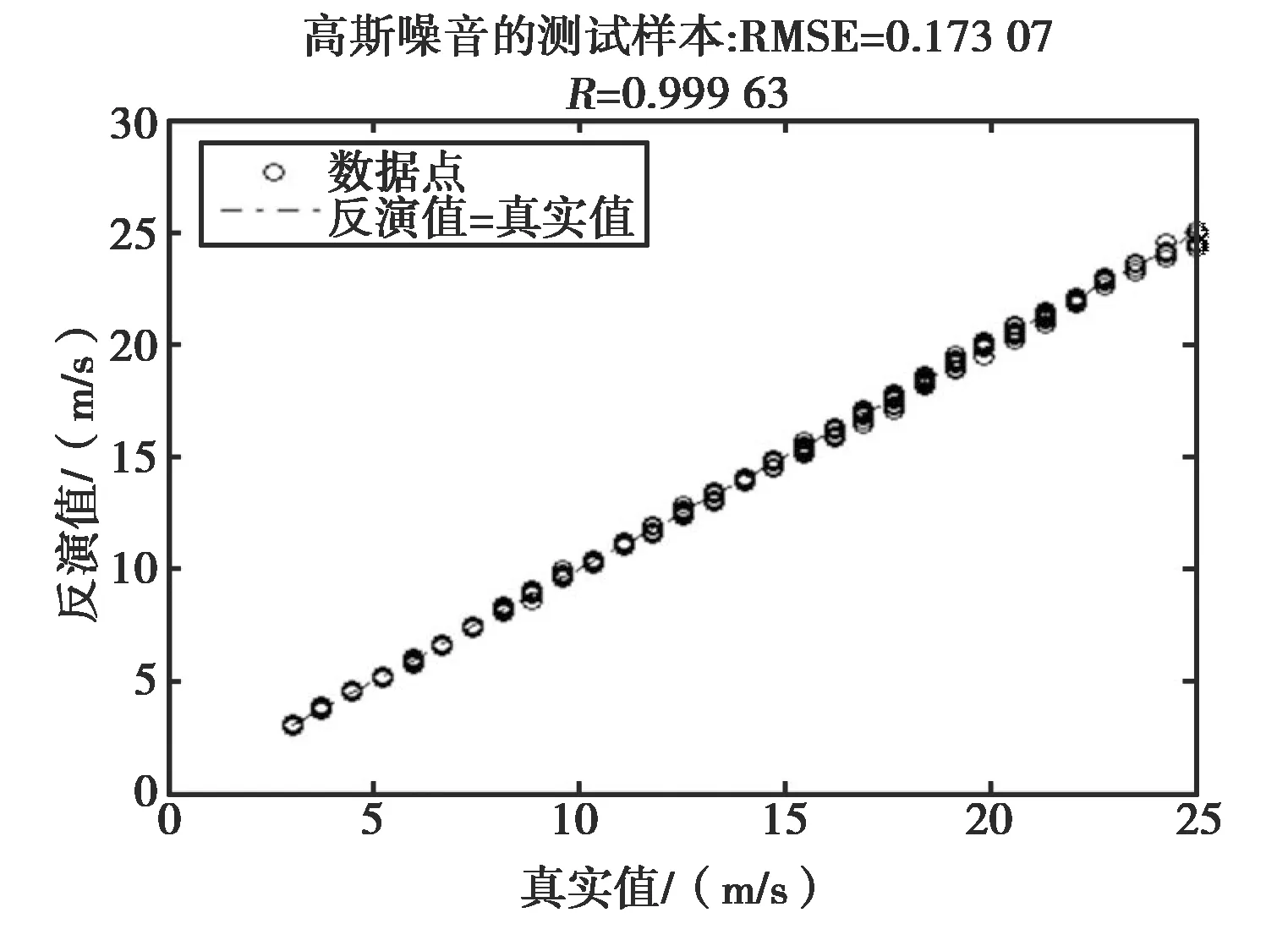
(a) D=0.3

(b) D=0.6

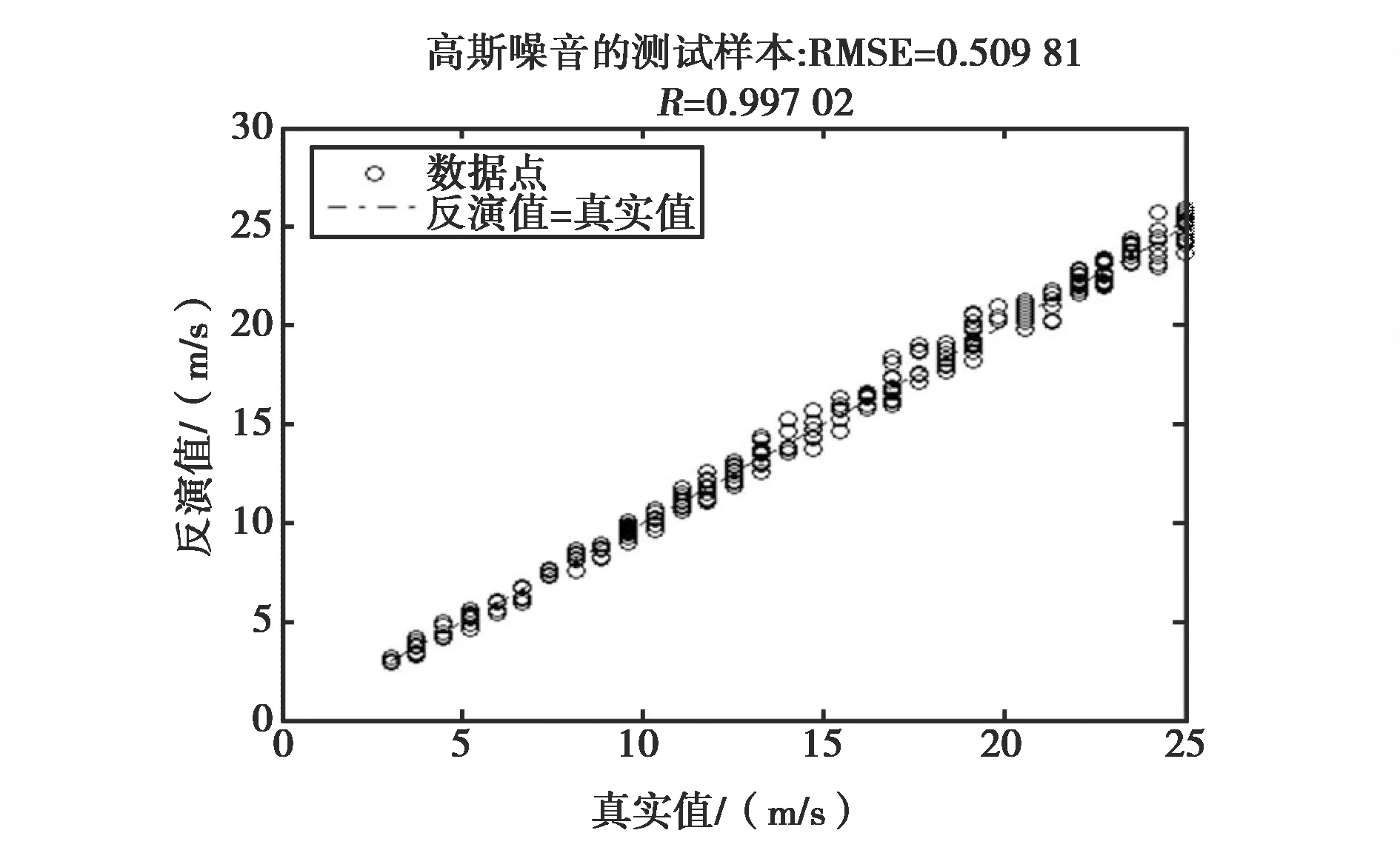
(c) D=0.9图8 高斯噪声下C波段的风速反演结果

表3是不同D时,SVM方法反演结果的误差比较.从表中可以看出,随着噪声的增大,其反演相关系数有所降低,RMSE有所增加，但整体反演精度仍然保持在一个较高的精度上,这也表明本文提出的SVM方法有较好的泛化能力和抗噪声性能.

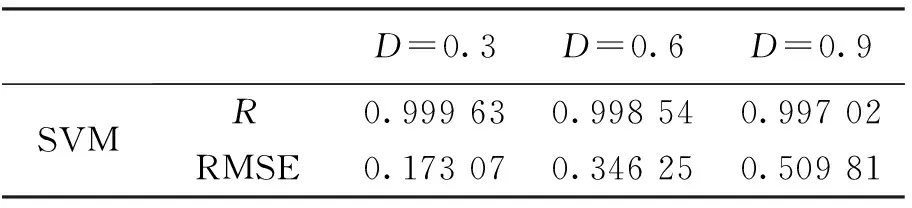
表3 三种不同噪声水平下SVM反演结果误差比较

4.2 盐度反演结果与分析

针对于盐度的反演,首先我们分别选取L波段和C波段下的双极化后向散射系数作为SVM的输入来进行盐度反演分析,然后再将同极化后向散射系数的比值作为SVM的输入来进行盐度反演分析,最后考虑将两种波段结合对盐度进行反演研究.

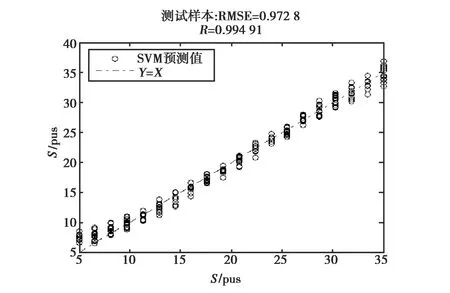
(a) 双极化散射系数

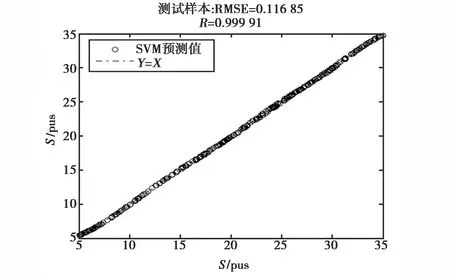
(b) 同极化散射系数比值图9 L波段下两种方案盐度反演结果

图9(a)、(b)分别是L波段下两种不同方案的盐度反演结果.从图中可看出,当采用双极化后向散射系数作为数据信息时,盐度反演的相关系数为0.994 91,RMSE为0.972 8,而采用同极化后向散射系数的比值作为SVM输入时,盐度反演的相关系数为0.999 91,RMSE为0.116 85,其反演精度明显高于前者,这也表明,由于采用同极化后向散射系数比值作为样本信息,有效降低了风驱粗糙海面的影响,提高了SVM反演模型的精度.

图10(a)、(b)分别是C波段下两种不同方案的盐度反演结果.可以看出,第二种反演方案(同极化散射系数比值)结果要明显好于第一种反演方案(双极化散射系数).同时,与L波段反演结果相比,由于C波段少了一个雷达入射角,样本数据信息不够丰富,使得C波段下的两种方案的反演模型精度要低于L波段.这也表明,当对海水盐度进行SVM反演建模时,宜采用双雷达入射角,并把同极化后向散射系数比值作为SVM的输入数据.

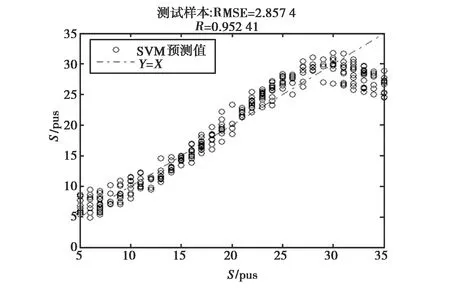
(a) 双极化散射系数

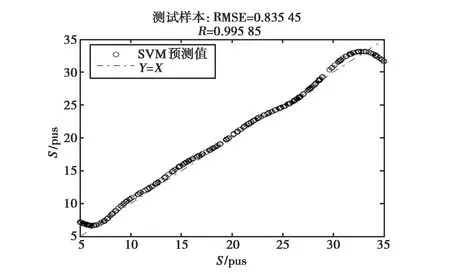
(b) 同极化散射系数比值图10 C波段下两种方案盐度反演结果

图11是双波段、三个入射角下,双极化后向散射系数作为SVM输入数据时海水盐度的反演结果,图12是双波段、三入射角下,同极化后向散射系数比值作为SVM输入数据时海水盐度的反演结果.从图中来看,基于双频率、三入射角下双极化的反演方案与C波段双极化的反演方案大致一致,但两种方案的反演精度都低于L波段、双入射角下双极化的反演精度.同时,比较图11和图12,在双波段反演框架下,当采用同极化后向散射系数的比值作为SVM输入数据信息时,明显提高了盐度的反演精度.

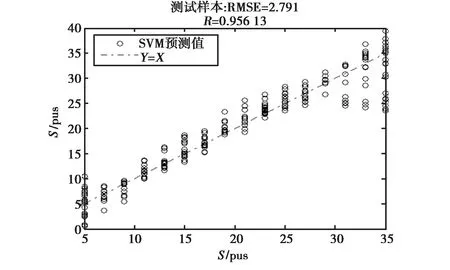
图11 双频率双极化下盐度的反演结果

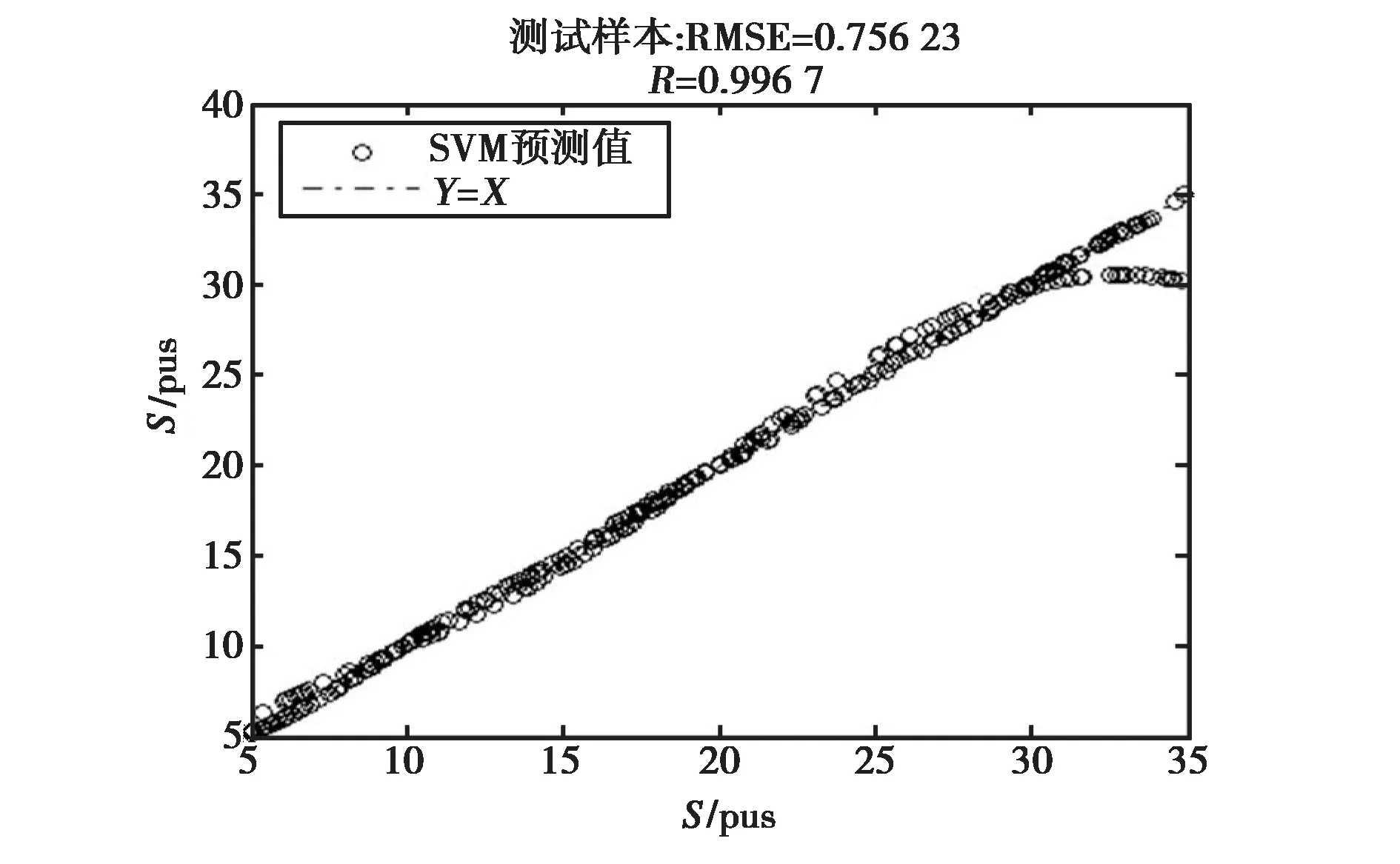
图12 双频率同极化比值下盐度的反演结果

从上述反演结果可分析得出,同极化散射系数比值作为SVM的输入时,三种方案反演精度均明显好于双极化后向散射系数作为输入时的反演精度,并且,在同极化散射系数比值的方案中,L波段的反演精度要优于C波段及双波段下的反演精度.因此,针对于海表盐度的反演,宜采用L波段、双入射角,且应把同极化散射系数比值作为SVM的输入数据.

5 结 论

本文利用双尺度方法结合支持向量机技术对海面风速及海表盐度进行了反演研究.以双尺度(TSM)作为前向模型,数值模拟不同海况参数下的后向散射系数,并以此作为SVM的输入样本.考虑不同雷达参数对风驱粗糙海面微波散射特性的差异,针对风速和盐度设计了多种反演方案.反演结果表明,针对于风速的反演,C波段双极化的反演方案精度最高;针对于海表盐度的反演,L波段同极化散射系数比值的反演方案精度最高.同时,本文也检验了SVM反演方法的抗噪声性能,表明本文提出的基于SVM的海况参数反演方法有较好的泛化能力和抗噪声性能.

[1]ATLAS R, HOFFMAN R N, LEIDNER S M, et al.The effects of marine winds from scatterometer data on weather analysis and forecasting[J].Bulletin of the American meteorological society, 2001, 82(9)：1965-1990.

[2]LAGERLOEF G, COLOMB F R, LEVINE D M, et al.The Aquarius/SAC-D mission：designed to meet the salinity remote sensing challenge[J].Oceanography, 2008, 21(1)：68-81.

[3]OSAMU I, MASANOBU S.An L-band ocean geophysical model function derived from PALSAR[J].IEEE transactions on geoscience and remote sensing, 2009, 47(7)：1925-1936.

[4]SIMON H Y, STEVE J D, ALEXANDER G F, et al.Passive and Active L-band microwave observations and modeling of ocean surface winds[J].IEEE transactions on geoscience and remote sensing, 2010, 48(8)：3087-3100.

[5]SIMON H Y, JULIAN C.Sea surface and wind retrieval using combined passive and active L-band microwave observations[J].IEEE transactions on geoscience and remote sensing, 2012, 50(4)：1022-1032.

[6]RIVAS M B, STOFFELEN A, ZADELHOFF G J, et al.The benefit of HH and VV polarizations in retrieving extreme wind speeds for an ASCAT type scatterometer[J].IEEE transactions on geoscience and remote sensing, 2014, 52(7)：4273-4280.

[7]ZOU J H, XIE X T, ZHANG Y, et al.Wind retrieval processing for HY-2A microwave scatterometer[C]//Proceedings of the IEEE Geoscience and Remote Sensing Symposium.Greece, 2014：5160-5163.

[8]TANG W Q, YUEH S, FORE A, et al.Aquarius combined active passive algorithm for ocean surface salinity and wind retrieval[C]//Proceedings of the General Assembly and Scientific Symposium.Greece, 2014：1-4.

[9]SAID F, JOHNSEN H, CHAPRON B, et al.An ocean wind Doppler model based on the generalized curvature ocean surface scattering model[J].IEEE transactions on geoscience and remote sensing, 2015, 53(12)：6632-6638.

[10]CLARIZIA M P, RUF C S, JALES P, et al.Spaceborne GNSS-R minimum variance wind speed estimator[J].IEEE transactions on geoscience and remote sensing, 2014, 52(11)：6829-6843.

[11]周旋, 叶小敏, 于暘, 等.基于GNSS-R的海面风速探测技术研究[J].电子与信息学报, 2013, 35(7)：1575-1580.

ZHOU X, YE X M, YU Y, et al.Sea surface wind speed measurement using GNSS reflection signal[J].Journal of electronics &information technology, 2013, 35(7)：1575-1580.(in Chinese)

[12]CHEN K S, TZENG Y C, CHEN P C.Retrieval of ocean winds from satellite scatterometer by a neural network[J].IEEE transactions on geoscience and remote sensing, 1999, 37(2)：247-256.

[13]林明森, 宋新改, 彭海龙, 等.散射计资料的风场神经网络反演算法研究[J].国土资源遥感, 2006, 68(2)：8-11.

LIN M S, SONG X G, PENG H L, et al.Neural network wind retrieval from scatterometer data[J].Remote sensing for land &resources, 2006, 68(2)：8-11.(in Chinese)

[14]解学通, 郁文贤, 郭丽青, 等.基于遗传算法的微波散射计海面风矢量反演研究[J].海洋通报, 2008, 27(4)：1-11.

XIE X T, YU W X, GUO L Q, et al.Research on Genetic algorithm based on ocean wind vector retrieval for microwave scatterometer[J].Marine science bulletin, 2008, 27(4)：1-11.(in Chinese)

[15]王署曜, 楚晓亮, 徐坤, 等.OS081H高频地波雷达系统海面风向反演实验研究[J].电子与信息学报, 2014, 36(6)：1400-1405.

WANG S Y, CHU X L, XU K, et al.Experimental research on inversion of wind direction with HFSWR OS081H[J].Journal of electronics &information technology, 2014, 36(6)：1400-1405.(in Chinese)

[16]GABARRO C, FONT J, CAMPS A, et al.Sea surface salinity and wind speed retrieval from a tower-based L-band radiometer in the NW mediterranean[C]//Proceedings of the IEEE on Remote Sensing.Spain, 2002:761-769.

[17]AMMAR A, LABROUE S, OBLIGIS E, et al.Sea surface salinity retrieval for the SMOS mission using neural networks[J].IEEE transactions on geoscience and remote sensing, 2008, 46(3)：754-764.

[18]卢红丽, 王振占, 殷晓斌.利用SMOS卫星数据反演海洋盐度方法研究[J].遥感技术与应用, 2014, 29(3)：401-409.

LU H L, WANG Z Z, YIN X B.Research of the sea surface salinity retrieval method based on SMOS data[J].Remote sensing technology and application, 2014, 29(3)：401-409.(in Chinese)

[19]严明, 严卫, 王迎强, 等.基于微波遥感的海表面盐度探测机制研究进展[J].遥感信息, 2015, 30(2)：17-25.

YAN M, YAN W, WANG Y Q, et al.Progress in sea surface salinity probe technology based on microwave remote sensing[J].Remote sensing information, 2015, 30(2)：17-25.(in Chinese)

[20]VAPNIK V.Statistical learning theory[M].New York：Wiley, 1998.

[21]TONG Y B, YANG D K, ZHANG Q H.Wavelet kernel support vector machines for sparse approximation[J].Journal of electronics (China), 2006, 23(4)：539-542.

[22]ZHANG L, LIN F, ZHANG B.Support vector machine learning for image retrieval[C]//Proceedings of the IEEE on Image Processing.Greece, 2001：107-118.[23]LEOPOLD E, KINDERMANN J.Text categorization with support vector machines.How to represent texts in input space?[J].Machine learning, 2002, 46：423-444.

[24]IPLIKCI S.Support vector machines-based generalized predictive control[J].International journal of robust and nonlinear control, 2006, 16(5)：813-862.

[25]许小剑, 李晓飞, 刁桂杰, 等.时变海面雷达目标散射现象学模型[M].北京：国防工业出版社, 2013：10-53.

[26]郭立新, 王蕊, 吴振森.随机粗糙面散射的基本理论与方法[M].北京：科学出版社, 2009：56-61.

[27]MEISSNER T, WENTZ F J.The complex dielectric constant of pure and sea water from microwave satellite observations[J].IEEE transactions on geoscience and remote sensing, 2004, 42(9)：1836-1849.

张清河 (1969-),男,湖北人，教授,博士,主要研究方向为电磁散射与逆散射、微波对地遥感、雷达海洋遥感等.

梁伟博 (1989-),男,河北人，硕士研究生,主要研究方向为电磁场数值计算、雷达海洋遥感等.

Inversion study of the rough sea surface wind speed and sea surface salinity based on the support vector machine

ZHANG Qinghe LIANG Weibo

(CollegeofScience,ThreeGorgesUniversity,Yichang443002,China)

In this paper, the support vector machine(SVM) regression techniques are applied to the inversion of sea state parameters (e.g.salinity and wind speed of the sea surface).The two scale model (TSM) is used to simulate backscattering coefficients of the rough sea surface with different radar parameters.After the sensitivity analysis, the L band (1.4 GHz) and the C band (6.8 GHz) are selected with appropriate angles as radar parameters.Then a variety of schemes of inversion are designed, in which single-frequency dual-polarization double angle, dual-frequency dual-polarization double angle and the ratio between the VV and HH polarization backscattering coefficients are chosen respectively as the samples information.After appropriate training, the SVM forecasting model is applied to inverse the salinity and wind speed of the sea surface.As shown by the results, at the C band, the inversion of the sea surface wind speed bears the highest accuracy, whereas at the L band, the inversion of the sea surface salinity demonstrates the highest accuracy when the ratio between backscattering coefficients is chosen as the samples in-formation.The anti-noise performance of the SVM model is also examined, and the results show that the SVM model performs favorably in the sea state parameter inversion problem.

support vector machine (SVM);two scale model(TSM);inversion;sea surface wind speed;sea surface salinity

张清河, 梁伟博.基于支持向量机的粗糙海面风速及海表盐度反演研究[J].电波科学学报,2016,31(5):896-905.

10.13443/j.cjors.2015102601

ZHANG Q H, LIANG W B.Inversion study of the rough sea surface wind speed and sea surface salinity based on the support vector machine [J].Chinese journal of radio science,2016,31(5):896-905.(in Chinese).DOI：10.13443/j.cjors.2015102601

2015-10-26

国家自然科学基金(61179025)

O451;TN99

A

1005-0388(2016)05-0896-10

联系人：张清河 E-mail:zhangqh6973@163.com