国家效用函数下的存款保险制度绩效评价

孟世超

(西南财经大学 中国金融研究中心，四川 成都 611130)



国家效用函数下的存款保险制度绩效评价

孟世超

(西南财经大学 中国金融研究中心，四川 成都 611130)

我国在2015年5月推出的存款保险制度需要一个合理的模式对其进行绩效考量，这一考量依赖国家效用函数的正确构设。构建了同时考虑“基点”和“效用变动值”的国家效用函数，将其分解为社会利润效用、稳定效用、发展效用、政府利润效用四个子函数。研究表明：存款保险制度使国有银行效率损失减少，而使其他银行效率损失增加，但只要前者减少的程度大于后者增加的程度，存款保险制度都是成功的。通过对国家监管部门与存款保险机构的博弈分析，论证了异于传统观点的“只要存款保险机构放松警惕，政府监管部门就必定选择调查”的策略，并给出了相应的参考建议。

国家效用；存款保险；绩效评价；挤兑现象；监管博弈

一、已有国家效用函数的缺陷

当前学术界，不少学者将国家(或政府)的效用函数类比于企业部门进行改造，但最终亦跳不出收入支出的框架[1]。这些研究将政府视为营利性的企业，税费和罚款为其收入，调查成本与国家保险基金的给付为其支出，在构造了净利润函数的基础上，代入效用函数模型，并以此认为得到了国家的效用函数，进而以这样的函数衡量存款保险制度的种种优劣，甚至质疑其存在的必要性[2]。

国家不是营利的企业，国家衡量效用损益的角度不仅仅是流动在政府部门中的、以货币计量的收入和支出。先前学者的研究，显然是忽视了政府地位的超脱性。政府代表国家，其效用函数必定具备国家属性，社会综合的收支以及社会的稳定程度与发展水平，这些因素都应该包括在政府的效用函数之中。只有这样设定，政府才是国家的政府，否则它仅仅是一个完全自利的且拥有超越其他经济实体权力的不公平的竞争者。

当前多数学者的研究，仅仅考虑了政府部门自身的收支，而未将全社会的收支包括在内；即使少数研究令国家效用函数涵盖了其他部门的收支，对社会稳定和发展的效用亦鲜有论及。如此得来的国家效用，无异于政府部门自己的效用，或是政府部门与其他部门效用的加总或平均[3]。纵使囊括了社会各部门，也单是效率意义上的效用，而未能涉及稳定与发展。很难相信一个不完整的国家效用函数能够合理评价存款保险制度的运行绩效。因此，理论界亟须建立真正涵盖存款保险国家属性的国家效用函数，从而为评价存款保险制度的运行效果提供一个基本准则。

二、新国家效用函数的构建与说明

在充分考虑了前人研究构设的国家效用函数漏洞的基础上，本文结合国家的超脱地位，兼顾社会总体收益、社会经济稳定与发展的要素，从而构建新的国家效用函数。

(一)国家效用函数的构建

1.国家效用函数的一般形式

本文设国家效用函数为G，G= G0+ΔG。G0表示实行存款保险之前初始的国家效用，ΔG则表示实行存款保险之后国家效用的变动。由于除政府自身外，存款保险制度只涉及存款人、存款机构与存款保险机构三个主体，因此ΔG部分也由这三个主体的效用变动和对社会的稳定发展影响组成。

2.国家效用函数的分解

现定义ΔG1、ΔG2、ΔG3、ΔG4分别表示社会利润效用、稳定效用、发展效用、政府利润效用的变动值。ΔG=((γ1ΔG1)2+ (γ2ΔG2)2+(γ3ΔG3)2+(γ4ΔG4)2)1/2，γ1、γ2、γ3、γ4分别表示计算总效用变动的权重。设fi、gi、hi(i=1，2，3，4)分别代表存款人、银行与存款保险机构的效用函数。其中ΔG1、ΔG2、ΔG3、ΔG4均为fi、gi、hi(i=1，2，3，4)的变动值Δfi、Δgi、Δhi(i=1，2，3，4)的函数。

(1)ΔG1的分解

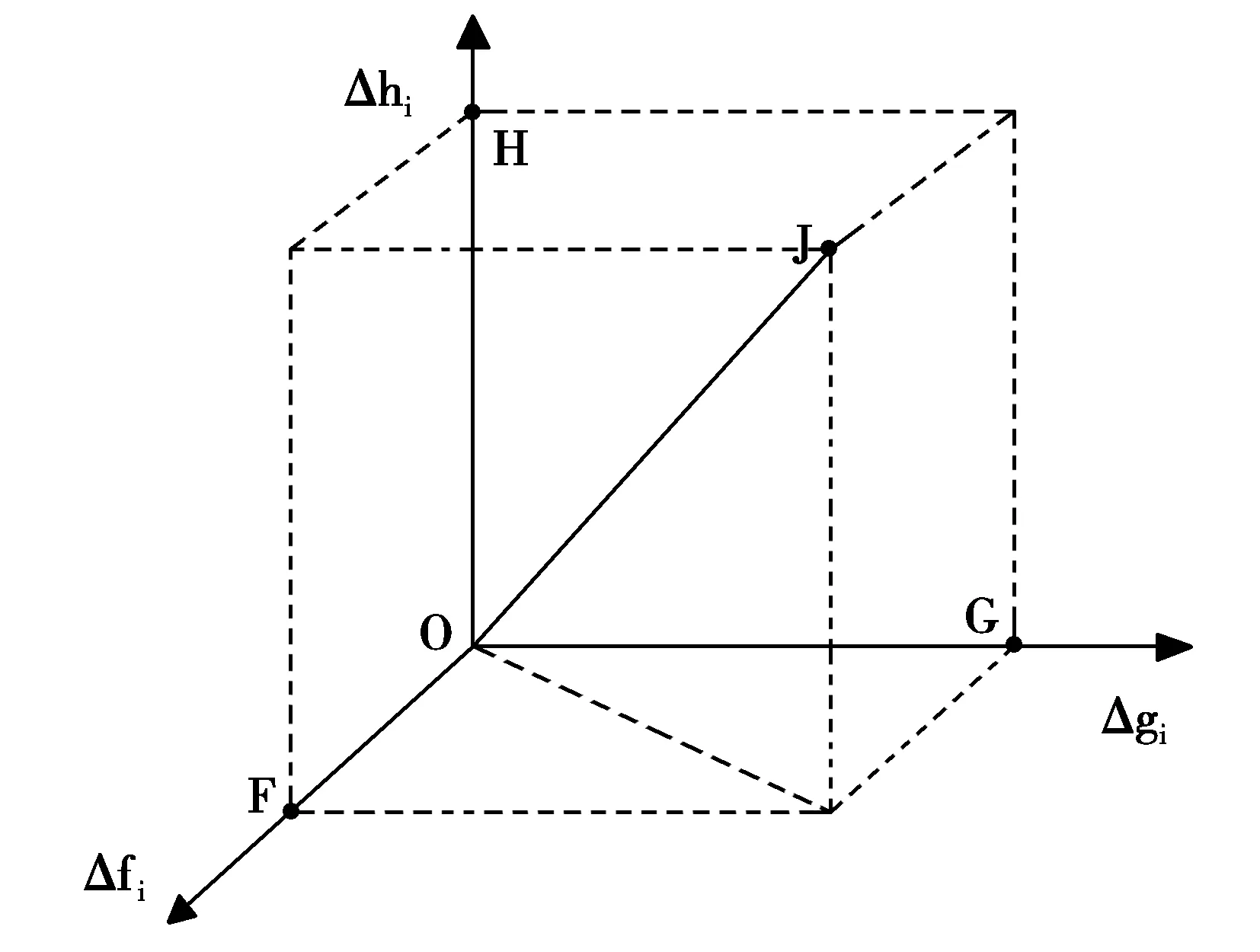
设Δf1=p*f((1+r1)E)+ (1-p)*q*f((1+r2)E)+ (1-p)*(1-q)*f((1+r1)E)- f*1，其中p为银行出险的平均概率，q为银行出险却不倒闭的概率，E为储户存款总额，r1、r2、r3分别表示银行不出险、出险却不倒闭、出险且倒闭情形下储户存款的收益率，r3

Δg1=g(Ym+Ye-Ce-(Cpj-C*pj)-λE)- g*1，g*1表示实行存款保险之前的效用水平，Ym表示银行的投资收益，Ye表示银行的其他收益，Ce表示银行的其他成本，(Cpj-C*pj)表示留存在银行的风险成本，λE表示银行缴纳的存款保险费。

Δh1=h(λE +Zm-C’e-(λE/(λE+J))Cp)- h*1，h*1表示实行存款保险之前的效用水平，λE表示存款保险机构收入的保费金额，Zm表示存款保险机构的其他收入，C’e表示存款保险机构的其他成本，(λE/(λE+J))Cp表示银行出险时由存款保险机构赔付的部分。

ΔG1由Δf1、Δg1、Δh1三部分组成，现对ΔG1进行几何加权平均：ΔG1=((η11Δf1)2+ (η12Δg1)2+(η13Δh1)2)1/2。其中，ηij(i=1，2，3，4；j=1，2，3)表示计算综合效用变化的权重。

(2)ΔG2的分解

Δf2=f(S*)- f*2，S表示存款保险后存款人受到的保障水平，f*2表示实行存款保险之前的效用水平。

Δg2=g(-Cs-Cm)- g*2，Cs表示银行的挤兑风险，Cm表示银行的投资风险，g*2表示实行存款保险之前的效用水平。

Δh2= h(-C’s-C’m)- h*2，C’s表示银行向存款保险机构转移的挤兑风险，C’m表示银行向存款保险机构转移的投资风险，h*2表示实行存款保险之前的效用水平。

ΔG2由Δf2、Δg2、Δh2三部分组成，现对ΔG2进行几何加权平均：ΔG2=((η21Δf2)2+ (η22Δg2)2+(η23Δh2)2)1/2。其中，ηij(i=1，2，3，4；j=1，2，3)表示计算综合效用变化的权重。

(3)ΔG3的分解

Δf3=G(δWf-(1-δ)Wf) - G*3f，Wf表示存款人的全部投资资产，δ表示其投资到有前景行业的比例，由于发展水平的效用不能通过存款人的效用函数衡量，这里代入国家效用函数，G*3f表示实行存款保险前的初始效用水平。

Δg3=G(θWg-(1-θ)Wg) - G*3g，Wg表示银行的全部投资资产，θ表示其投资到有前景行业的比例，由于发展水平的效用不能通过银行的效用函数衡量，这里代入国家效用函数，G*3g表示实行存款保险前的初始效用水平。

Δh3=G(ξWh-(1-ξ)Wh) - G*3h，Wh表示存款保险机构的全部投资资产，ξ表示其投资到有前景行业的比例，由于发展水平的效用不能通过存款保险机构的效用函数衡量，这里代入国家效用函数，G*3h表示实行存款保险前的初始效用水平。

ΔG3由Δf3、Δg3、Δh3三部分组成，现对ΔG3进行几何加权平均：ΔG3=((η31Δf3)2+ (η32Δg3)2+(η33Δh3)2)1/2。其中，ηij(i=1，2，3，4；j=1，2，3)表示计算综合效用变化的权重。

(4)ΔG4的分解

Δf4=G(Tf-(J/(λE+J))Cp) - G*4f，Tf表示存款人向国家缴纳的税费，G*4f表示实行存款保险前的初始效用水平，其余变量定义参照上文的设定。由于涉及政府自身的收支，这里只能代入国家效用函数。

Δg4=G(Tg) - G*4g，Tg表示银行向国家缴纳的税费，G*4g表示实行存款保险前的初始效用水平，因存款保险的偿付直接面向存款人而非银行，因此国家的存款保险给付体现在存款人的函数而非银行的函数中，由于涉及政府自身的收支，这里只能代入国家效用函数。

Δh4=G(Th-LR1- max(LR2-Cp，0)-LI) - G*4h，Th表示存款保险机构向国家缴纳的税费，LI表示政府监管存款保险机构的成本，G*4h表示实行存款保险前的初始效用水平，由于涉及政府自身的收支，这里亦只能代入国家效用函数。

ΔG4由Δf4、Δg4、Δh4三部分组成，现对ΔG4进行几何加权平均：ΔG4=((η41Δf4)2+ (η42Δg4)2+(η43Δh4)2)1/2。其中，ηij(i=1，2，3，4；j=1，2，3)表示计算综合效用变化的权重。

(二)国家效用函数构建的相关说明

1.变量的引入顺序

本文定义的上述公式均不考虑变量引入的顺序，只根据相应的权重予以加总，然后将加总后的结果作为一个整体代入另一个效用函数。这是因为，效用函数具有很强的“锚定效应”，即决策者以初始点为原点，收益增加则效用递减地增加，收益减少则效用递增地减少，而这种关系很大程度上取决于原点的选择；而收益变动的总和一定时，若考虑原点位置的移动，则必将受引入顺序的影响。如图1所示：

图1 考虑顺序的效用变化

设曲线CA、CB、CC、CD、CE分别表示5条位于不同原点或不同变化方向的效用曲线。假设原始的收益为R2，若先减少收益至R1，则效用沿曲线CA降落到位置UD；又增加收益使其恢复到R2，则效用沿曲线CA上升到UB。而若进行相反的操作，先提高收益至R3， R3-R2=R2-R1，则效用沿最初的曲线CA升至UE；又减少收益使其回到R2，则效用沿曲线CA降落至UC处。虽然最终的收益没有改变，但不同顺序下的最终效用却不相同，有UC

然而，国家效用函数中内部变量参数的引入并无确定的顺序可言，因此区分顺序没有意义。且不同的引入顺序导致不同的效用结果，因此将每个变量单独代入效用函数再累加是不可取的。本文于是采用将所有变量按权重加总，再以一个整体代入效用函数的方式，避免了引入顺序对最终效用的影响。又因这些变量的引入并不存在不同情形下的概率分布问题，所以也不会产生“期望效用”与“效用期望”的纷争。

2.引入权重的平均变化量公式

由于不同变量在效用函数中的地位不同，本文为其设置了不同的权重。又由于效用函数本身即是非线性的，因此本文尝试使用非线性的平均公式来求得均值。本文定义的均值公式在ΔG1(i=1，2，3，4)的计算中，具有几何意义。如图2所示：

图2 国家效用函数下均值公式的几何意义

图2中，横轴、纵轴和竖轴分别表示Δfi、Δgi和Δhi(i=1，2，3，4)，每一数轴的每一单位乘以相应的权重。假定Δfi、Δgi和Δhi分别落在F、G和H位置，则按本文提供的均值算法，最终的均值可以用图中长方体的体对角线OJ表示。若三轴表示变量的绝对取值而非变动值，则初始位置不再为原点O，但最终的变动均值依旧可表示为从初始点出发的一个与上述长方体全等几何体的体对角线，两者仅仅有位置的平移差异，但长度相等。

ΔG的计算是四维的，不再具有几何意义，但原理与ΔGi(i=1，2，3，4)的计算毫无差异。由于考虑了权重和非线性关系的均值算法，使得国家效用函数的变量修正更加合理，符合实际。

三、新国家效用函数下的存款保险制度运行与监管评价

借助新的国家效用函数，本文对我国存款保险制度的部分运行绩效和监管方法予以相应的评价。下文主要就存款保险制度对存款人挤兑现象的作用以及存款保险机构监管银行的策略选择问题进行论述。

(一)存款保险制度作用于挤兑现象的效果度量

1.挤兑行为效率损失的度量

本文引入一个“银行效率损失函数”Lost，作为国家发展效用G3在银行部门的分量g3的一种反向表示分解方式，即以效率损失近似作为银行发展效用的减项。该函数对银行部门的效率损失又进行再度分解，具有如下特征：

第一，Lost函数由两个子函数Lost1与Lost2按存款份额的加权平均数构成。第二，Lost1表示银行过迟破产的效率损失，自变量为延迟破产银行受到完全保障的存款金额；Lost2表示纯粹挤兑导致银行过早破产引起的效率损失，自变量为银行的破产临界点K。第三，前者为自变量的增函数，后者为自变量的减函数。

2.存款保险制度引入前的效率损失衡量

根据我国银行实际受到保障的程度，这里将我国银行归为两类，一类为“确定保障银行”，即受到全额隐性担保的国有商业银行；另一类则为“无保障银行”，即不受国家信用保护的中小银行与信用合作社。设前者吸收的存款占存款总额的比重为ω，吸收存款金额为L1S，受到全额保障，且因受到国家信用的保护，不存在公众挤兑的可能；后者吸收的存款占存款总额的比重为(1-ω)，吸收存款金额为L1C，挤兑情形下的破产临界值为K。则原有的效率损失函数为：Lost(ω，L1S，K)=ωLost1(L1S)+(1-ω)Lost2(K)。

3.存款保险制度引入后的效率损失衡量

实施存款保险制度后，假设最高保证总限额为D，每个账户为d，银行总资产为A，存款为L1，非存款负债为L2，资本金为P，现金为C，则银行效率损失函数中有四个参数将发生变化：

一是ω的改变。储户的存款在两类银行间分配的比重变为ω’，原有的效率损失函数化为Lost(ω’,L1s,K)=ω’Lost(L1s)+(1-ω’)Lost2(K)，由于存款保险使得储户承受风险的能力增强，他们更愿意将存款转移至收益更高的“无保障银行”，因此国有商业银行吸收的存款将减少，比重较先前下降，因此ω’<ω，反之，1-ω’>1-ω。

二是L1S的改变。“确定保障银行”吸收的存款变为L’1S，且L’1S

三是Lost1(D)的产生。原先无保障的银行增加了总额度为D的存款保险保护，因非存款债权人的监管松懈而引致的效率损失出现，记作Lost1(D)。

四是K的改变。因储户挤兑而造成的效率损失降低，破产临界值变为K’，K’>K。

因此，原有的效率损失函数化为：

Lost(ω’，L’1S，D，K’)=ω’Lost1(L’1S)+(1-ω’)[Lost1(D)+Lost2(K’)]。

由于Lost的两个子函数中Lost1单调增加，Lost2单调减少，因此有Lost1(L’1S)1-ω，而有

(1-ω’)[Lost1(D)+Lost2(K’)]>(1-ω)Lost2(K)。

比较前后两个公式，可知存款保险使得国有银行的效率损失减少，其他银行的效率损失增加，但只要前者减少的程度大于后者增加的程度，即ωLost1(L1S)-ω’Lost1(L’1S)>(1-ω’)[Lost1(D)+Lost2(K’)]-(1-ω)Lost2(K)，存款保险制度都是成功的。因此，上式可作为衡量存款保险制度在缓解存款人挤兑问题上运行绩效的评价准绳。

(二)政府监管部门的策略选择

此处所指的监管部门，是凌驾于存款保险机构之上的监管机构，代表国家利益。其监管策略的选择依赖于国家效用函数而非自身的效用函数。考虑到这一点，政府监管部门与存款保险机构之间的博弈与学术界流行的模式有所差异，策略选择也随之不同。

1.政府监管部门—存款保险机构博弈

(1)博弈模型的假设

a. 只考虑政府监管部门(1个主体)与1家存款保险机构；

b. 政府监管部门按照国家效用函数G进行决策，存款保险机构按照其自身的效用函数M进行决策；

c. 政府监管部门具有对存款保险机构“调查”“不调查”两种策略选择，存款保险机构具有对银行风险“严格”“纵容”两种策略选择；

d. 存款保险机构选择“纵容”策略，即对高风险银行不进行保险合同的变更，必然为存款保险机构负责人收受相关银行贿赂的结果，此外存款保险机构不具备纵容高风险银行的任何动机；

e. 若政府监管部门进行调查，则存款保险机构负责人的纵容行为必定被发现，政府监管部门将对负责人予以严厉处罚。

(2)博弈过程与结果

根据上述假设，政府监管部门与存款保险机构负责人之间的博弈矩阵见表1：

表1 政府监管部门与存款保险机构负责人的博弈矩阵

其中Mj和Gj(j=1，2，3，4)分别表示存款保险机构负责人与政府监管部门在不同策略下的效用。由上述分析可得，最理想的均衡点应该为(M2，G2)。然而，现实中，该点却未必成立。

若政府监管部门选择调查，此时M1> M3，因此存款保险机构负责人必将选择严格监管；而若存款保险机构负责人选择严格监管，出于巨额调查费用的考虑，即G1< G2，政府监管部门将选择不予调查。因此，(M1，G1)、(M2，G2)都不为均衡点。

若存款保险机构负责人选择受贿和纵容，出于国家效用的考虑，政府监管部门仍将选择调查(此时恒有G4< G3，负责人纵容高风险银行给整个社会造成稳定性效用的减少，因此这里不存在风险成本大于调查成本时明知负责人纵容银行却不予调查的情况，这与流行的策略选择模式不同)；而若政府监管部门选择调查，则M1> M3，存款保险机构负责人将选择严格监管。因此，(M3，G3)、(M4，G4)都不为均衡点。

所以，博弈矩阵中的4个点(M1，G1)、(M2，G2)、(M3，G3)、(M4，G4)都不可能成为均衡点。该博弈并不存在纯策略均衡。

2.政府在博弈中的策略选择

虽然上述结论与学术界流行的博弈研究相似，但政府监管部门的策略选择却与流行的结论存在不小的差别。由于本文建立的国家效用函数考虑到社会各部门、整体经济稳定与健康发展的一系列因素，因此只有在存款保险机构严格监管的情形下，G2> G1成立，政府监管部门才会选择不予调查；而一旦存款保险机构放松对银行的

监管，则必有G4< G3，因为对高风险的纵容势必导致社会承受风险的增加，而风险上升导致国家效用的减少程度远大于成本下降对国家效用的增加。也即是：只要存款保险机构放松警惕，政府监管部门就必定会选择调查。这与传统研究认为政府往往因调查成本过大，虽明知风险上升而仍旧选择放弃调查的结论相反。因此，借助新的国家效用函数后，政府监管部门将更倾向于为社会整体的长远利益而认真调查，绝非因调查的高成本而畏首畏尾。

四、总结与建议

我国近期推出的存款保险制度需要一个合理的模式对其进行绩效考量，这一考量依赖国家效用函数的正确构设。而原有的研究思路狭窄，政策建议有欠合理，为此本文从构建全新的国家效用函数入手，从而提出一个相对全面的绩效评价方法。

本文建立的国家效用函数涵盖了政府利润、社会利润、稳定、发展4个关键因素。借助此函数，本文给出了评价存款保险制度在减少挤兑问题中表现的标准，并论述了政府监管部门对存款保险机构调查监督方面的策略选择。

本文有以下建议：一是将存款人与银行的道德风险控制在合理范围，使得存款保险制度在减少挤兑方面单向减少效率损失，增加国家效用；二是政府监管部门要树立“国家意识”，对存款保险制度的考核也应兼顾社会稳定与发展方面，而非单单考虑自身的收付盈亏。

[1]钱小安.存款保险的道德风险、约束条件与制度设计[J].金融研究，2004，(8)：21-27.

[2]Karels G and McClachey C.Deposit Insurance and Risk-Taking Behavior in the Credit Union Industry[J].Journal of Banking and Finance,1999,23(1)：105-134.

[3]张玉梅，赵 勇.隐形存款保险向显性存款保险转变对银行道德风险的影响[J].南方经济，2006，(5)：104-111.

责任编校：张 静，罗 红

2016-02-05

孟世超，女，河南郑州人，博士，研究方向为风险投资。

F840.65

A

1007-9734(2016)02-0100-05